World Journal of Mechanics
Vol.4 No.4(2014), Article ID:44627,10 pages DOI:10.4236/wjm.2014.44012
A Theoretical Analysis of Thermoelastic Damping Model in Laminated Trilayered Circular Plate Resonators
Yuxin Sun*, Jialing Yang, Yan Jiang
The Solid Mechanics Research Center, Beihang University, Beijing, China
Email: *yxsun@buaa.edu.cn
Copyright © 2014 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/


Received 9 January 2014; revised 8 February 2014; accepted 4 March 2014
ABSTRACT
Thermoelastic damping of the axisymmetric vibration of laminated circular plate resonators is discussed in this paper. Based on the classical laminated plate theory assumptions, the governing equations of coupled thermoelastic problems are established for axisymmetric out-of-plane vibration of trilayered circular plate. The analytical expression for thermoelastic damping is obtained and the accuracy is verified through comparison with finite element analysis results. Then some simplifications are made on the theoretical model.
Keywords:Thermoelastic Damping, Circular Plate, Resonator, Trilayer

1. Introduction
Miniaturized resonators are widely used as sensors and modulators in microand nanoelectromechanical systems (MEMS/NEMS) [1] [2] . For resonators, it is desired to design and construct systems with loss of energy as little as possible [3] . Various energy dissipation mechanisms exist in MEMS and NEMS [4] -[6] . While, thermoelastic damping is an intrinsic dissipation mechanism and it will not be affected by the changes of environment. Therefore, structural damping is essentially dominated by thermoelastic damping (TED), and it is more important to study the effect of thermoelastic damping on the mechanical behavior of MEMS.
Zener [7] firstly developed the thermoelastic damping theory by studying the transverse vibration of homogeneous and isotropic thin beam. Thermoelastic damping arises from thermal currents generated by compression/decompression in elastic media. The bending of the reed causes dilations of opposite signs to exist on the upper and lower halves. One side is compressed and heated, and the other side is stretched and cooled. Thus, in the presence of finite thermal expansion, a transverse temperature gradient is produced. The temperature gradient generates local heat currents, which cause increase of the entropy of the reed, lead to energy dissipation.
Many researchers have studied the thermoelastic damping effect in resonators made of single materials [8] -[10] . However, in many applications, it is necessary to coat a resonator with thin metallic layers to improve the optical reflectivity or enhance the electrical conductivity [11] [12] . Examples include the probe of scanning force microscopy which is Au-coated Si microcantilevers, and SiC microreonators coated by Al [13] . In such cases, the resonators must be treated as laminated composites of layered thin films. Up to date, a little of work relative to the thermoelastic damping in laminated composite resonators has been reported. Bishop and Kinra [14] first developed analysis of thermoelastic damping in laminated rectangular plate. Later on, Vengallatore and his co-author studied thermoelastic damping in bilayered [15] and symmetric, three-layered [11] beam resonators. All the analysis started from the definition that the magnitude of thermoelastic damping is the ratio of the energy dissipated per cycle of vibration to the maximum elastic energy stored in the body.
This paper deals with thermoelastic damping effects on the out-of-plane vibration of laminated circular plate resonators, which are common elements in many sensors and resonators [16] . Different from the above work, the expression of thermoelastic damping is obtained from the complex vibration frequency.
2. Formulation of the Problem
Consider a laminated circular plate symmetrically composed of three layers with thermally perfect interfaces. The cylindrical coordinate system 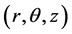 is applied to study the vibration of the trilayered circular plate. The neutral surface is put on the
is applied to study the vibration of the trilayered circular plate. The neutral surface is put on the 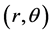 coordinate plane, and the z-axis normal to the neutral surface. The structure and the coordinate system are illustrated in Figure 1. The two outer layers are made of the same materials and have an identical thickness. The radius of the resonator is
coordinate plane, and the z-axis normal to the neutral surface. The structure and the coordinate system are illustrated in Figure 1. The two outer layers are made of the same materials and have an identical thickness. The radius of the resonator is . The thicknesses of the inner and outer layers are
. The thicknesses of the inner and outer layers are 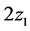 and
and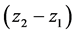 , respectively. Hence, the volume fraction of the outer layer is
, respectively. Hence, the volume fraction of the outer layer is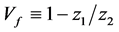 .
.
For axisymmetric circular plate, the displacement and the temperature are independent of , so we define
, so we define ,
,  and
and  to be the displacement components along the radial, circumferential and axial directions, respectively, and
to be the displacement components along the radial, circumferential and axial directions, respectively, and 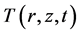 the temperature field. In equilibrium, the resonator is assumed to be unstrained, unstressed and keeps at environmental temperature
the temperature field. In equilibrium, the resonator is assumed to be unstrained, unstressed and keeps at environmental temperature 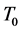 everywhere. Assuming small strains and displacements, the relationship between the displacement components can be given by
everywhere. Assuming small strains and displacements, the relationship between the displacement components can be given by
 (1)
(1)
where 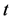 is time.
is time.
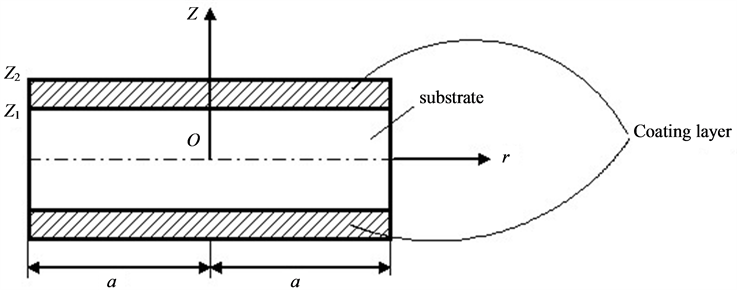
Figure 1. Schematic illustration of the trilayered circular plate and the coordinate system.
The strain components are given by
 (2)
(2)
We assume plane stresses for the laminated circular plate, which leads to
 (3)
(3)
Thus the cubical dilation  for each layer is obtained as
for each layer is obtained as
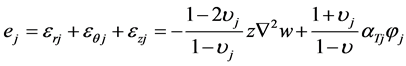 (4)
(4)
where the subscript 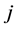 ranges from 1 to 3, with the convention that
ranges from 1 to 3, with the convention that 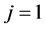 denotes the substrate layer (the inner layer) and
denotes the substrate layer (the inner layer) and 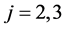 denotes the two covering layers (the outer layers);
denotes the two covering layers (the outer layers); 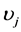 and
and 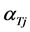 denote the Poisson’s ratio and the coefficient of thermal expansion, respectively; and
denote the Poisson’s ratio and the coefficient of thermal expansion, respectively; and 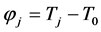 is the temperature increment of the resonator as a function of
is the temperature increment of the resonator as a function of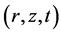 .
. 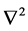 is the Laplace operator, and is expressed as
is the Laplace operator, and is expressed as
 (5)
(5)
Now, the thermal conduction equation containing the thermoelastic coupling term for each layer has the following term:
 (6)
(6)
where ,
,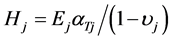 ;
;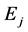 ,
, 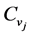 and
and 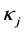 are the Young’s modulus, the specific heat at constant volume and the thermal conductivity , respectively.
are the Young’s modulus, the specific heat at constant volume and the thermal conductivity , respectively.
Typically, the second item of  can be ignored. For silicon at 300 K, the ratio of the first item to the second item of
can be ignored. For silicon at 300 K, the ratio of the first item to the second item of 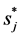 is 1776, and the ratios for Au, Al, Cu and Ag are about 30. Although the ratios for metals are not very large, still we can replace
is 1776, and the ratios for Au, Al, Cu and Ag are about 30. Although the ratios for metals are not very large, still we can replace 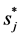 by
by 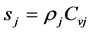 without introducing large error to the final results. In Section 4, we will first compare the results of the two cases: the heat conduction equation with
without introducing large error to the final results. In Section 4, we will first compare the results of the two cases: the heat conduction equation with 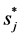 (case I) and that with
(case I) and that with 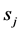 (case II).
(case II).
Noting that thermal gradients in the plane of the cross-section along the plate thickness direction are much larger than gradients along the radial direction, we can ignore the term  in Equation (6) [2] . Hence, Equation (6) reduces to
in Equation (6) [2] . Hence, Equation (6) reduces to
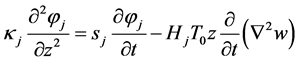 (7)
(7)
Note that the second term of the right side of Equation (7) is an odd function of , and the operator
, and the operator  on the left side is symmetric in
on the left side is symmetric in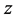 , it follows that the temperature field
, it follows that the temperature field 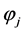 is an odd function of
is an odd function of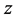 , and
, and 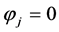 at
at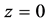 . [14] Thus, it is sufficient to consider only the upper half of the plate,
. [14] Thus, it is sufficient to consider only the upper half of the plate, 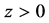 while solving the thermal conduction Equation (7).
while solving the thermal conduction Equation (7).
The stress components of each layer are given by the constitutive equation as
 (8)
(8)
Now, the moments of flexure in the substrate layer are
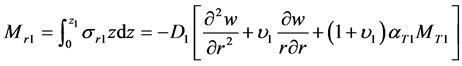 (9)
(9)
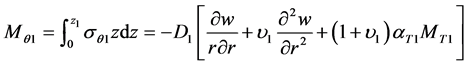 (10)
(10)
where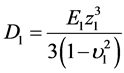 ,
,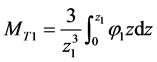 .
.
And the moments of flexure in the outer layers are
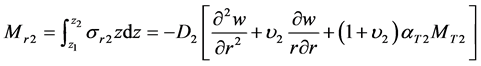 (11)
(11)
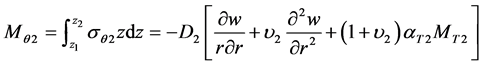 (12)
(12)
where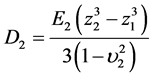 ,
,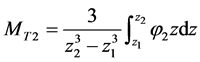 .
.
Hence the resultant moments of flexure of the plate are as follows:
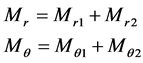 (13)
(13)
The equation of transverse motion for an axisymmetric circular plate is
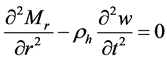 (14)
(14)
where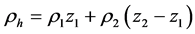 , and
, and 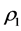 and
and 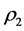 are the density of the substrate and covering layers, respectively.
are the density of the substrate and covering layers, respectively.
Substitute Equations (9)-(13) into Equation (14), we can get the differential equation of the out of plane vibration of the laminated circular plate:
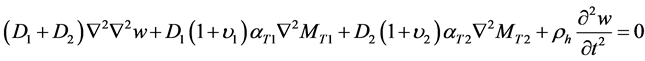 (15)
(15)
In summary, the governing equations of this problem are composed of Equations (7) and (15).
3. Solution of the Governing Equations
To calculate the effect of thermoelastic coupling on the vibrations of a circular plate, we solve the coupled thermoelastic Equations (7) and (15) for the case of harmonic vibrations. We set
 (16)
(16)
where 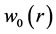 is the mode shape. In general, the frequency
is the mode shape. In general, the frequency 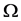 is complex, the real part
is complex, the real part 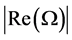 giving the new eigenfrequencies of the plate in the presence of thermoelastic coupling effect, and the imaginary part
giving the new eigenfrequencies of the plate in the presence of thermoelastic coupling effect, and the imaginary part  giving the attenuation of the vibration.
giving the attenuation of the vibration.
Substituting Equation (16) into Equation (15) yield the following equation:
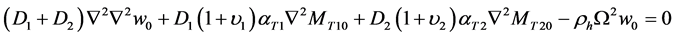 (17)
(17)
where
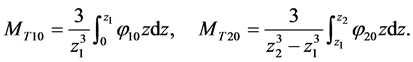 . (18)
. (18)
It is assumed that the upper and lower surfaces are adiabatic and the interfaces are thermally perfect. Taking into account the property of 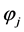 related to
related to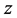 , the boundary and interface conditions are
, the boundary and interface conditions are
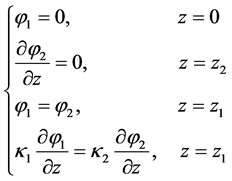 (19)
(19)
Following the standard integral transform techniques presented by Özisik [17] , the solution of the boundary value problem, in terms of Equation (16), was found to be:
 (20)
(20)
where
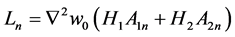 (21)
(21)
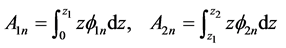 (22)
(22)
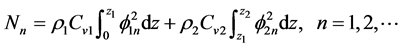 (23)
(23)
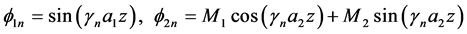 (24)
(24)
where
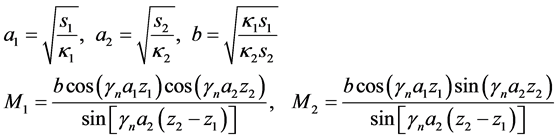 (25)
(25)
The eigenvalues 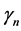 is obtained from the transcendental equation
is obtained from the transcendental equation
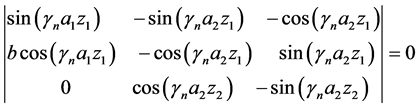 (26)
(26)
From Equations (16) and (20), it is obtained
 (27)
(27)
Substitution of Equations (18) and (27) into Equation (16) yields,
 (28)
(28)
where
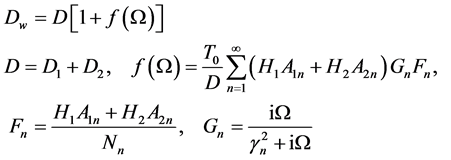 (29)
(29)
For a laminated circular plate with the boundary fully clamped, the boundary conditions are
 (30)
(30)
The solution of Equation (28) in combination with Equation (30) gives the value of frequency considering thermoelastic coupling effect
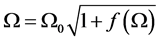 (31)
(31)
where  is the frequency when the thermoelastic coupling effect is ignored, and
is the frequency when the thermoelastic coupling effect is ignored, and
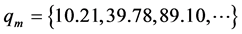 .
.
Because the difference between 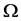 and
and 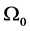 is small, we can replace
is small, we can replace  in Equation (31) by
in Equation (31) by  and expand Equation (31) into a series up to the first order. That is
and expand Equation (31) into a series up to the first order. That is
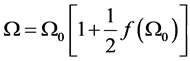 (32)
(32)
So, we can easily extract the real and imaginary parts of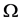 , which are shown as
, which are shown as
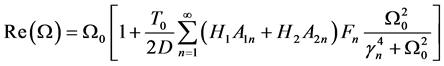 (33)
(33)
 (34)
(34)
Thus, we arrive at an expression of thermoelastic damping in a symmetric trilayered circular plate, which is given by
 (35)
(35)
4. Results and Discussions
In this section, we will present some numerical results for the relationship between 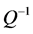 and the radius of the plate and make some discussions about this model. From [11] [18] , we can get the thermodynamic properties of the used materials under room temperature (300 K), which are listed in Table 1. For abbreviation, we will only consider the fundamental vibration mode, namely, the
and the radius of the plate and make some discussions about this model. From [11] [18] , we can get the thermodynamic properties of the used materials under room temperature (300 K), which are listed in Table 1. For abbreviation, we will only consider the fundamental vibration mode, namely, the 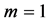 mode.
mode.
First, the influence of the reduction of 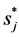 to
to 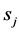 is checked. The heat conduction equation with
is checked. The heat conduction equation with 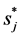 is named case I and that with
is named case I and that with 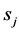 is named case II. Figure 2 shows the themoelastic damping,
is named case II. Figure 2 shows the themoelastic damping, 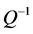 , against the
, against the
Table 1. Mechanical and thermal properties of the materials (300 K).


Figure 2. Comparison of the two cases: the heat conduction with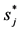 , and the heat conduction with
, and the heat conduction with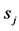 .
.
radius of the plate, . The solid line represents the case I, and the dashed line for case II. The structure of the laminate composite is metal/Si/metal and the thickness of the metal and Si layers are
. The solid line represents the case I, and the dashed line for case II. The structure of the laminate composite is metal/Si/metal and the thickness of the metal and Si layers are 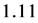 and 20 mm, respectively, which corresponds to
and 20 mm, respectively, which corresponds to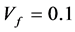 . The metals are Au and Ag in Figure 2(a), Figure 2(b), respectively. It is shown that the results of the two cases are in good agreement.
. The metals are Au and Ag in Figure 2(a), Figure 2(b), respectively. It is shown that the results of the two cases are in good agreement.
To verify the accuracy of the model proposed in the paper, we also simulate this problem through the commercial software COMSOL Multiphysics. In the calculation, the resonator is composed of Au/Si/Au, the thicknesses of the Si and Au layers are 20 and 1.11 mm, respectively. We check the slice of the normal strain along the 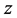 direction of the circulate plate with the radius of 400 mm, as shown in Figure 3, and find that the strain component
direction of the circulate plate with the radius of 400 mm, as shown in Figure 3, and find that the strain component  is nearly zero in the substrate layer of Si, while it varies significantly in the Au layer.
is nearly zero in the substrate layer of Si, while it varies significantly in the Au layer.
According to this result, the heat conduction equation should be modified into
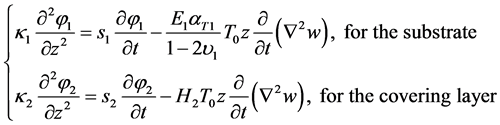 (36)
(36)
Now, the governing equations are composed of Equations (7) and (43), and the expression of 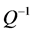 can be obtained through repeating the derivation in Section 3, except for replacing
can be obtained through repeating the derivation in Section 3, except for replacing 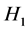 by
by . This is defined as Model 2. Correspondingly, the model composed of Equations (7) and (15) is defined as Model 1.
. This is defined as Model 2. Correspondingly, the model composed of Equations (7) and (15) is defined as Model 1.
Figure 4 shows the calculation results based on Model 1, Model 2 and the finite element method (FEM), where the abscissa is the plate radius and the ordinate is the thermoelastic damping.
It is shown in Figure 4 that the results can be classified into three regions: (1)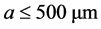 , the results of Model 1 and Model 2 are nearer to each other; (2)
, the results of Model 1 and Model 2 are nearer to each other; (2) , the results of Model 2 and FEM analysis are nearer to each other; (3)
, the results of Model 2 and FEM analysis are nearer to each other; (3) , the results of the three methods are almost the same.
, the results of the three methods are almost the same.
In addition, the variation of  on the thickness of Si layer is also calculated, and the results are shown in Figure 5. The calculation results based on Model 1, Model 2 and FEM for the structure of Au/Si/Au are compared. The radius of the plate is 400 mm in Figure 5(a) and 800 mm in Figure 5(b), and the volume fraction of coating layer is maintained as
on the thickness of Si layer is also calculated, and the results are shown in Figure 5. The calculation results based on Model 1, Model 2 and FEM for the structure of Au/Si/Au are compared. The radius of the plate is 400 mm in Figure 5(a) and 800 mm in Figure 5(b), and the volume fraction of coating layer is maintained as .
.
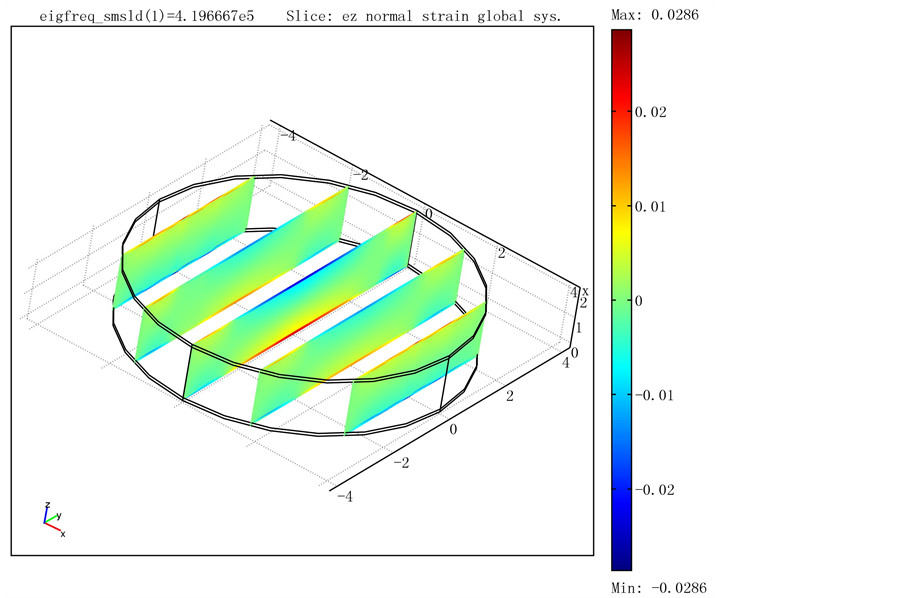
Figure 3. Slice of the normal strain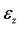 .
.
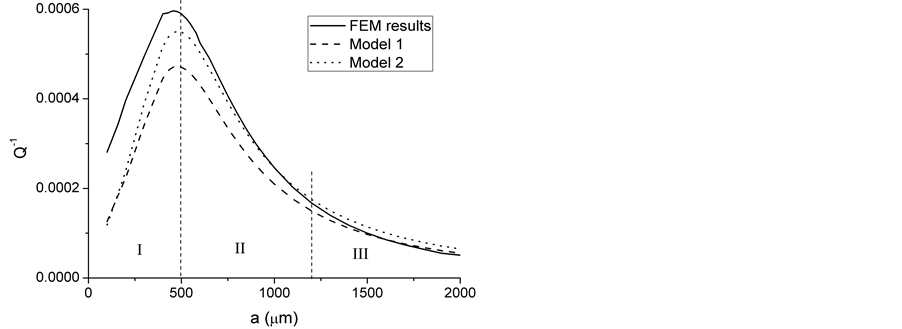
Figure 4. Comparison of the analytical solution and FEM analysis.
Comparing Figure 4, Figure 5, it is shown that the three regions in Figure 4 are related to the value of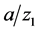 . In the case of small value of
. In the case of small value of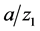 , the results of Model 1 and Model 2 are nearer to each other. On the other hand, in the case of large value of
, the results of Model 1 and Model 2 are nearer to each other. On the other hand, in the case of large value of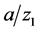 , the results of Model 2 and FEM analysis are nearer to each other.
, the results of Model 2 and FEM analysis are nearer to each other.
In summarize, the results of both models are in good agreement with FEM results, and those of Model 2 agree better than those of Model 1. To further illustrate the influence of the normal strain along the 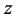 direction, the distribution of
direction, the distribution of 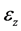 at the center of the plate along the
at the center of the plate along the  direction is calculated for plates with different radius. The variation tendency of
direction is calculated for plates with different radius. The variation tendency of  on
on  is the same for plates with different radius. As an example, the results for the plate with the radius of 200 and 400 mm are shown in Figure 6. It can be found that the normal strain in Si layer is quite small, however, the strain in Au layer is much larger, and it increases suddenly at the interface. At the interface, the ratio of the strain of Si layer,
is the same for plates with different radius. As an example, the results for the plate with the radius of 200 and 400 mm are shown in Figure 6. It can be found that the normal strain in Si layer is quite small, however, the strain in Au layer is much larger, and it increases suddenly at the interface. At the interface, the ratio of the strain of Si layer,  , to that of Au layer,
, to that of Au layer,  , increases a little as the radius of
, increases a little as the radius of
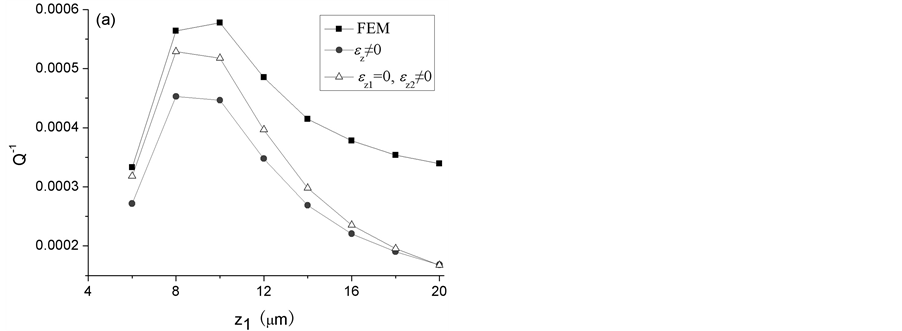
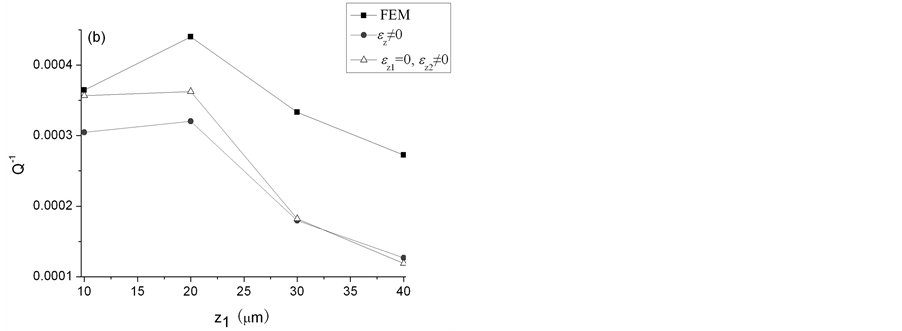
Figure 5. Variation of  on the thickness of Si layer based on Model 1, Model 2 and FEM. The radius of the plate is (a)
on the thickness of Si layer based on Model 1, Model 2 and FEM. The radius of the plate is (a)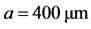 , (b)
, (b) .
.
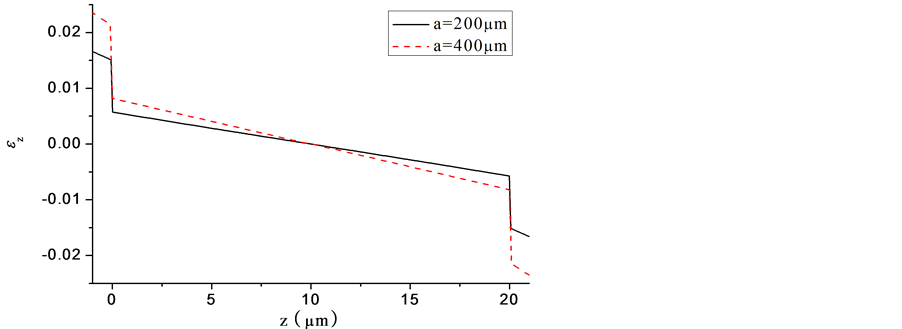
Figure 6. Distribution of  at the center of the plate along the
at the center of the plate along the 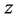 direction for the plates with radius of 200 and 400 mm.
direction for the plates with radius of 200 and 400 mm.
the plate increases. The value is about 0.38. So, we can ignore the normal strain  in Si layer and obtain good results, as shown in Figure 4.
in Si layer and obtain good results, as shown in Figure 4.
5. Conclusion
As MEMS and NEMS technologies evolve, there is an increasing use of sophisticated structural geometries and advanced materials, especially laminated composites of layered thin film. A detailed theory is presented for thermoelastic damping in trilayered circular plate resonators. The analytical expression for thermoelastic damping in these structures is obtained. Then the accuracy of the model is verified through comparison with finite element analysis results and some simplifications are made on the theory. In the heat conduction equation, the coefficient of ratio of temperature obtained from the plane stress assumption is composed of two items. It is found that the equation can be simplified by ignoring the item related to mechanical deformation. In addition, the strain along the thickness direction of Silicon can be ignored. Finally, the model is accurate for thin plate structures. However, the Mindlin model should be used for thick plate to derive the expression of thermoelastic damping.
Acknowledgements
The work described in this paper is financially supported by the National Natural Science Foundation of China under grant number 11002017 and 11032001 and the Fundamental Research Funds for the Central Universities under grant number YWF-13-JQCI-001. The authors would like to gratefully acknowledge these supports.
References
- Srikar, V.T. and Spearing, S.M. (2003) Materials Selection in Micromechanical Design: An Application of the Ashby Approach. Journal of Microelectromechanical Systems, 12, 3-10. http://dx.doi.org/10.1109/JMEMS.2002.807466
- Sun, Y.X. and Tohmyoh, H. (2009) Thermoelastic Damping of the Axisymmetric Vibration of Circular Plate Resonators. Journal of Sound and Vibration, 319, 392-405. http://dx.doi.org/10.1016/j.jsv.2008.06.017
- Lifshitz, R. and Roukes, M.L. (2000) Thermoelastic Damping in Microand Nanomechanical Systems. Physical Review B, 61, 5600-5609. http://dx.doi.org/10.1103/PhysRevB.61.5600
- Srikar, V.T. and Spearing, S.M. (2003) Material Selection for Microfabricated Electrostatic Actuators. Sensors and Actuators A, 102, 29-85. http://dx.doi.org/10.1016/S0924-4247(02)00393-X
- Ferguson, A.T., Li, L. and Nagaraj, V.T. (2005) Modeling and Design of Composite Free-Free Beam Piezoelectric Resonators. Sensors and Actuators A, 118, 63-69. http://dx.doi.org/10.1016/j.sna.2004.08.001
- Evoy, S., Olkhovets, A. and Sekaric, L. (2000) Temperature-Dependent Internal Friction in Silicon Nanoeletromechanical Systems. Applied Physics Letters, 77, 2397-2399. http://dx.doi.org/10.1063/1.1316071
- Zener, C. (1937) Internal Friction in Solids I. Theory of Internal Friction in Reeds. Physical Review, 52, 230-235. http://dx.doi.org/10.1103/PhysRev.52.230
- Sun, Y.X. and Saka, M. (2010) Thermoelastic Damping in Micro-Scale Circular Plate Resonators. Journal of Sound and Vibration, 329, 328-337. http://dx.doi.org/10.1016/j.jsv.2009.09.014
- Sun, Y.X., Fang, D.N. and Soh, A.K. (2006) Thermoelastic Damping in Micro-Beam Resonators. International Journal of Solids and Structures, 43, 3213-3229. http://dx.doi.org/10.1016/j.ijsolstr.2005.08.011
- Wong, S.J., Fox, C.H.J. and McWilliam, S. (2006) Thermoelastic Damping of the In-Plane Vibration of thin Silicon Rings. Journal of Sound and Vibration, 293, 266-285. http://dx.doi.org/10.1016/j.jsv.2005.09.037
- Vengallatore, S. (2005) Analysis of Thermoelastic Damping in Laminated Composite Micromechanical Beam Resonators. Journal of Micromechanics and Microengineering, 15, 2398-2404. http://dx.doi.org/10.1088/0960-1317/15/12/023
- Bao, G. and Jiang, W. (1998) A Heat Transfer Analysis for Quartz Microresonator IR Sensors. International Journal of Solids and Structures, 35, 3635-3653. http://dx.doi.org/10.1016/S0020-7683(97)00235-7
- Huang, X.M.H., Zorman, C.A. and Mehregany, M. (2003) Nanodevice Motion at Microwave Frequencies. Nature, 421, 496. http://dx.doi.org/10.1038/421496a
- Bishop, J.E. and Kinra, V.K. (1997) Elastothermodynamic Damping in Laminated Composites. International Journal of Solids and Structures, 34, 1075-1092. http://dx.doi.org/10.1016/S0020-7683(96)00085-6
- Prabhakar, S. and Vengallatore, S. (2007) Thermoelsatic Damping in Bilayered Micromechanical Beam Resonators. Journal of Micromechanics and Microengineering, 17, 532-538. http://dx.doi.org/10.1088/0960-1317/17/3/016
- Berry, B.S. (1995) Precise Investigation of the Theory of Damping by Transverse Thermal Currents. Journal of Applied Physics, 26, 1221-1224. http://dx.doi.org/10.1063/1.1721877
- Özisik, M. (1980) Heat Conduction. John Wiley & Sons, New York.
NOTES

*Corresponding author.


