World Journal of Mechanics
Vol.4 No.1(2014), Article ID:42191,12 pages DOI:10.4236/wjm.2014.41002
A Probabilistic Approach for Studying the Reliability of Cementless Hip Prostheses in the Presence of Mechanical Uncertainties
Clermont Université, Université Blaise Pascal, Institut Pascal, Clermont-Ferrand, France
Email: labesse@moniut.univ-bpclermont.fr
Received October 14, 2013; revised November 16, 2103; accepted December 11, 2013
ABSTRACT
This paper presents a probabilistic approach for studying the reliability of cementless hip prostheses in the presence of mechanical uncertainties and its application to the investigation of the influence of bone-implant interface properties. The non-linear deterministic model of the bone-implant coupled system and its finite element implementation are described, and the proposed reliability analysis is exposed. It is demonstrated that the distribution (uniform, truncated Gaussian and truncated lognormal distribution) of the two chosen parameters and the truncation lengths have a minor influence on the Hasofer-Lind index. This index logically increases as the failure threshold increases. FORM and SORM approximations are compared with the results obtained using a crude Monte-Carlo method for the estimation of failure probability. The performance of three Monte-Carlo methods is studied in terms of the necessary number of FE calculations. The method based on the Directional Simulation (DS) technique is efficient and less time-consuming. The validity and operational capacity of the proposed approach would not be compromised by an increase in the number of uncertain parameters.
Keywords:Probabilistic Analysis; Cementless Hip Prosthesis; Bone-Implant Interface; Primary Stability
1. Introduction
The amount of relative micro-movement between bone and implant plays a crucial role in the success of Total Hip Replacement (THR) [1]. Ideally, to promote the Primary Stability of the prosthesis, the amount of relative micro-movement between bone and implant induced early after the operation, before any biological process takes place, must remain lower than a prescribed threshold. If not, the lack of Primary Stability may lead to the aseptic loosening of the implant [1]. The primary stability of a cementless hip stem is not only affected by the implant design, but also by biomechanical properties, among which the coefficient of friction at the bone-implant interface or the elastic properties of the cancellous bone are known to play a crucial role. The natural variability of these parameters has to be taken into account to predict the Primary Stability of the THR. This is practically unfeasible experimentally, due to the great number of tests which would have to be carried out. The combination of numerical models and probabilistic methods offers a promising alternative.
Probabilistic methods enable the estimation of the effects of parameter variability in the resulting statistical variation of the system response to be determined. Each parameter is generally represented as a random variable, and the propagation of their randomness into the system response is predicted. By understanding the distribution of performance, evaluations of quality and risk assessment can be performed. Recent studies have proposed probabilistic approaches to assessing the structural integrity of orthopaedic implants [2-8]. Previously, Browne et al. [9] applied reliability theory to aid in fracture mechanics-based life prediction procedures for a tibial tray component represented as a cantilever beam subjected to constant amplitude loading. Dar et al. [10] demonstrated how Taguchi and probabilistic methods could complement each other to account for uncertainties when predicting stresses with finite element analysis, in a study of a fixation plate represented as a cantilever beam. The femoral stem component of a total hip replacement has been the subject of several probabilistic structural integrity studies [11]. Bah and Browne [12] used an idealized cylindrical finite element model to represent an implanted cemented hip stem in order to assess the most likely failure mode and to identify which parameters had the largest contribution, where geometry, material properties and loading were considered as random variables. The latest studies concerning the application of probabilistic approaches to cementless hip prostheses have focused on the effect of femur characteristics and implant design geometry [13] or implant positioning on Primary Stability [14].
This paper presents a probabilistic approach for studying the reliability of cementless hip prostheses in the presence of mechanical uncertainties and its application to the investigation of the influence of bone-implant interface properties. In Section 2, the nonlinear deterministic model of the bone-implant coupled system and its finite element implementation are concisely presented. The uncertain parameters of the problem, the control variable and the associated failure criterion defining Primary Stability are then detailed. Section 3 is dedicated to the probabilistic modelling of the problem. Section 4 exposes the proposed reliability analysis. In Section 5, numerical experiments are presented in order to quantify the influence of the statistical characteristics of the random parameters, the Young modulus of the cancellous bone and the friction coefficient at the interface between the cancellous bone and the stem on the reliability of the bone-implant coupled system.
2. Deterministic Modelling
In this section we first concisely present the deterministic model used in this study, from its mechanical formulation to its practical implementation, as well as its finite element formulation. Then we highlight the uncertain parameters of the model, we introduce a failure criterion for the latter and we express this criterion in terms of the selected uncertain parameters.
2.1. Mechanical Formulation and Associated Numerical Model
The mechanical problem to solve consists of the contact with friction of two three-dimensional deformable bodies B1 and B2 occupying the domains V1 and V2 of ![]() with boundaries
with boundaries ![]() and
and . Denoting by
. Denoting by ![]() the contact surface between B1 and B2, and considering the principle of virtual work, this problem may be formulated in the following way (variational formulation):
the contact surface between B1 and B2, and considering the principle of virtual work, this problem may be formulated in the following way (variational formulation):
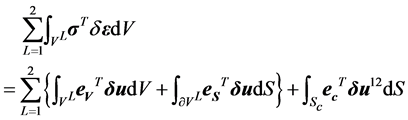 (1)
(1)
where ![]() and
and ![]() are the volume and surface measurements, respectively,
are the volume and surface measurements, respectively,  is the Cauchy stress vector defined as
is the Cauchy stress vector defined as ,
,
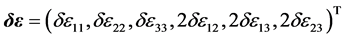 is the associated virtual strain vector corresponding to the imposed virtual displacement vector
is the associated virtual strain vector corresponding to the imposed virtual displacement vector![]() ,
,
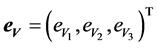 is the vector of known externally applied force per unit volume,
is the vector of known externally applied force per unit volume,  is the vector of the known externally applied surface tractions and
is the vector of the known externally applied surface tractions and  is the vector of the unknown surface tractions applied to body 1 due to its contact with body 2.
is the vector of the unknown surface tractions applied to body 1 due to its contact with body 2.
The term 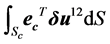 in Equation (1) corresponds to the virtual work due to contact tractions and
in Equation (1) corresponds to the virtual work due to contact tractions and 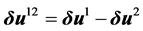 denotes the relative virtual displacement vector field of the two bodies in the contact zone.
denotes the relative virtual displacement vector field of the two bodies in the contact zone.
The contact tractions acting on the contact surface ![]() may be decomposed into normal and tangential components as follows:
may be decomposed into normal and tangential components as follows:
![]() (2)
(2)
where ![]() and
and  are the normal and tangential tractions, and
are the normal and tangential tractions, and 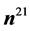 and
and ![]() are the normal and tangential unit vector fields associated with
are the normal and tangential unit vector fields associated with![]() .
.
Note that at this step all the parameters used are fields depending on the spatial coordinates![]() .
.
Let ![]() be the gap function for the contact surface pair. It is a scalar function defined as follows:
be the gap function for the contact surface pair. It is a scalar function defined as follows:
Let 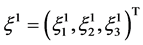 be the coordinates vector of point
be the coordinates vector of point
![]() of
of ![]() and
and 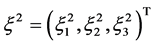 be the coordinates vector of point
be the coordinates vector of point ![]() of
of  such that:
such that:
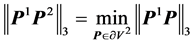 (3)
(3)
where ![]() denotes the canonical Euclidean norm on
denotes the canonical Euclidean norm on
![]() . Therefore,
. Therefore,  is the usual Euclidean distance from
is the usual Euclidean distance from ![]() to
to 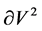 and
and ![]() is a function of
is a function of![]() . Then
. Then 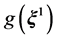 is defined as:
is defined as:
 (4)
(4)
where 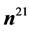 is the unit normal outward vector to
is the unit normal outward vector to  at point
at point![]() .
.
With this definition, the normal contact conditions can be written:
![]() (5)
(5)
where the last equation expresses the fact that the normal traction component is compressive, and exists only if the contact is effective i.e. if![]() .
.
The tangential contact conditions are taken into account by assuming that Coulomb’s law of friction holds locally on the contact surface. Let ![]() be the coefficient of friction. Coulomb’s law of friction is usually formulated as a function of the local tangential relative velocity at the contact interface. However, in the static case it can be reformulated using the relative tangential displacement
be the coefficient of friction. Coulomb’s law of friction is usually formulated as a function of the local tangential relative velocity at the contact interface. However, in the static case it can be reformulated using the relative tangential displacement 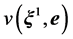 due to a loading increment
due to a loading increment ![]() of
of ![]() and
and![]() :
:
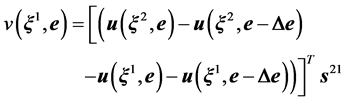 (6)
(6)
where ![]() is the unit tangential vector at point
is the unit tangential vector at point![]() .
.
Let us also define the non-dimensional variable 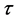 given by:
given by:
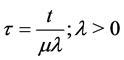 (7)
(7)
With this definition, Coulomb’s law of friction can be written:
![]() (8)
(8)
The constraint function method proposed by Bathe [15] is used to impose the normal and tangential contact conditions.
Let ![]() be a real-valued function of
be a real-valued function of ![]() and
and ![]() such that the solution of
such that the solution of ![]() satisfies the normal contact conditions, and let
satisfies the normal contact conditions, and let ![]() be a real-valued function of v and t such that the solution of
be a real-valued function of v and t such that the solution of ![]() satisfies the tangential contact conditions.
satisfies the tangential contact conditions.
Thus the initial problem (1) takes the form:
 (9)
(9)
The finite element formulation of this problem is achieved using the standard procedures exposed in reference [16]. The displacement field 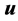 is approximated using an interpolation procedure based on nodal point displacements, leading to the classical expression:
is approximated using an interpolation procedure based on nodal point displacements, leading to the classical expression: ![]() , where
, where ![]() is the displacement interpolation matrix and
is the displacement interpolation matrix and ![]() is the vector of the nodal displacements.
is the vector of the nodal displacements.
Concerning the discretization of the contact conditions, the constraint function method proposed by Bathe [15] is adopted. This results in adding a nonlinear term to the initial problem, dependent on the unknown contact forces vector at the contact nodes of body![]() .
.
Denoting by ![]() this term, by
this term, by 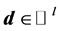 the global unknown vector gathering
the global unknown vector gathering ![]() and
and![]() , and by
, and by ![]() the prescribed conditions vector gathering the external nodal prescribed loads and the contact constraints, the displacement-based finite element formulation of the initial problem then takes the form:
the prescribed conditions vector gathering the external nodal prescribed loads and the contact constraints, the displacement-based finite element formulation of the initial problem then takes the form:
![]() (10)
(10)
where the nonlinear function ![]() from
from ![]() into
into ![]() is the mechanical operator, and the integer
is the mechanical operator, and the integer ![]() is the dimension of the discretized problem; that is to say, of the finite element model.
is the dimension of the discretized problem; that is to say, of the finite element model.
Equation (10) is solved using an incremental procedure coupled with the Newton-Raphson method. This leads to the calculation of the unknown vector  at loading increment
at loading increment ![]() from the solution
from the solution ![]() at increment
at increment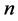 . At each step of this procedure, the incremental equation is obtained by linearizing Equation (10) about the last calculated state. Using the procedure described in [16], the matrix incremental equation obtained at iteration step
. At each step of this procedure, the incremental equation is obtained by linearizing Equation (10) about the last calculated state. Using the procedure described in [16], the matrix incremental equation obtained at iteration step ![]() is:
is:
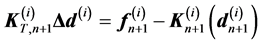 (11)
(11)
where 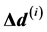 is the increment of unknown d at iteration step
is the increment of unknown d at iteration step![]() , and
, and  is given by:
is given by:
 (12)
(12)
where ![]() denotes the gradient with respect to
denotes the gradient with respect to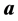 . The solution to Equation (11) gives the increment
. The solution to Equation (11) gives the increment 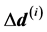 and therefore determines the value of the state vector
and therefore determines the value of the state vector 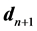 at iteration step
at iteration step![]() , that is:
, that is:
![]() (13)
(13)
The iterations are continued until a specified convergence criterion is satisfied.
Practically, this problem is solved using the FEMAPNASTRAN software package [17]. The stem and the bone are discretized using four-node tetrahedral elements leading to a model of 79067 elements and 18701 nodes (Figure 1).
A contact pair between the stem and the bone is defined in order to take into account the contact with friction between these two bodies. The host bone is subdi-

Figure 1. Mesh of the FE model used for the study of thefemur-cementless prosthesis coupled system: DePuy Corail®.
vided into two regions, corresponding respectively to the cortical and the cancellous zones. The femoral head and femoral stem are tied together. The femur is fully constrained at its distal part. Frictional contact at the bone-implant interface is taken into account, leading to nonlinear behaviour.
The position of the femur reproduces the standing position in vivo. The applied force is vertical and is progressively increased to a maximum value corresponding to the maximum load during a walk cycle of a 75 kg person in the unilateral compression position. The numerical results obtained are validated by comparison with in vitro test results [18].
2.2. Uncertain Parameters of the Model
Until now, all the quantities appearing in Equation (10) (i.e. the operator K and the vectors d and f) have been supposed to be deterministic, that is to say not affected by uncertainties.
We now assume that the known prescribed conditions vector f is deterministic and that two mechanical parameters of the operator K are uncertain: the Young’s modulus of the cancellous bone and the coefficient of friction at the interface between the cancellous bone and the femoral stem, respectively denoted 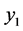 and
and![]() .
.
Therefore K is uncertain through these two parameters. Let  be the vector of
be the vector of ![]() gathering them. By hypothesis, K depends on
gathering them. By hypothesis, K depends on![]() . Consequently, from Equation (10), the unknown vector
. Consequently, from Equation (10), the unknown vector ![]() also depends on
also depends on ![]() and is therefore uncertain.
and is therefore uncertain.
2.3. Control Variable and Associated Failure Criterion
Formally, the solution to Equation (10) can be written:
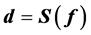 (14)
(14)
where ![]() is a nonlinear operation from
is a nonlinear operation from ![]() into
into ![]() such that:
such that:
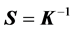 (15)
(15)
A control variable is a real variable, for example a scalar displacement (or a stress, or a strain) at a particular point of the studied mechanical system, whose value must be controlled within the framework of the reliability analysis of the system.
In this work, the chosen control variable is the Euclidean norm of maximum relative displacement between the femoral stem and the cancellous bone.
Let 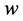 be such a variable. It depends on the unknown
be such a variable. It depends on the unknown ![]() through a relationship of the form:
through a relationship of the form:
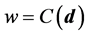 (16)
(16)
where C is a known function from ![]() into
into , called observation operator. Inserting Equation (14) into Equation (16) yields:
, called observation operator. Inserting Equation (14) into Equation (16) yields:
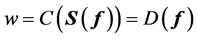 (17)
(17)
where ![]() is also a known function from
is also a known function from ![]() into
into . As a result,
. As a result, 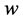 can also be viewed as a function of
can also be viewed as a function of![]() . Note that the functions C and D are known, in the sense that they are described by known numerical models.
. Note that the functions C and D are known, in the sense that they are described by known numerical models.
As seen in Section 2.2, the mechanical operator ![]() depends on the uncertain vector parameter
depends on the uncertain vector parameter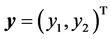 . As a result, its inverse
. As a result, its inverse 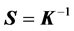 also depends on
also depends on![]() , as does the function
, as does the function![]() , as can be seen from Equation (17). Indicating this fact by the new notation
, as can be seen from Equation (17). Indicating this fact by the new notation ![]() and
and 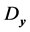 in the place of
in the place of ![]() and
and![]() , Equations (14) and (17) become:
, Equations (14) and (17) become:
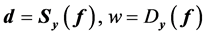 (18)
(18)
and, since ![]() is a constant vector of
is a constant vector of![]() , can be rewritten:
, can be rewritten:
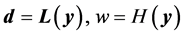 (19)
(19)
where  is a function from
is a function from ![]() into
into ![]() and
and ![]() is a function from
is a function from ![]() into
into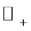 , such that
, such that![]() :
:
 (20)
(20)
Let ![]() be a given admissible value of
be a given admissible value of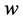 , called the failure threshold, and let
, called the failure threshold, and let 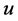 be the real variable such that:
be the real variable such that:
 (21)
(21)
Such a variable is called the safety margin associated with the control variable , and its sign defines two fundamental states for the mechanical model: the safe state if
, and its sign defines two fundamental states for the mechanical model: the safe state if ![]() and the failure state if
and the failure state if![]() . The value
. The value ![]() characterizes a limit situation called the failure limit state. According to Equation (19),
characterizes a limit situation called the failure limit state. According to Equation (19), 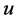 can be rewritten:
can be rewritten:
![]() (22)
(22)
where 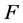 is a function from
is a function from ![]() into
into 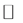 called the limit state function of the mechanical model. This function defines three specific subsets of
called the limit state function of the mechanical model. This function defines three specific subsets of![]() :
:
 (23)
(23)
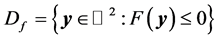 (24)
(24)
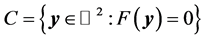 (25)
(25)
which verify:
![]() (26)
(26)
and which are respectively called the safe domain, the failure domain and the limit state curve.
The condition ![]() defining the failure state is the failure criterion associated with the control variable
defining the failure state is the failure criterion associated with the control variable 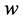 and its limit value
and its limit value![]() . The failure domain
. The failure domain 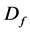 is the geometric representation of this criterion.
is the geometric representation of this criterion.
Let us note that, since the function 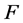 is only known numerically (through the finite element model described in Section 2.1), the sets
is only known numerically (through the finite element model described in Section 2.1), the sets![]() ,
, 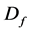 and
and ![]() can only be determined numerically.
can only be determined numerically.
3. Probabilistic Modelling
In the following, all the considered random variables (RV) are assumed to be defined on the same probability space![]() , where
, where ![]() is a sample space,
is a sample space, ![]() is a
is a 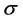 -algebra of subsets of
-algebra of subsets of ![]() and
and 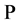 is a probability on
is a probability on![]() .
.
3.1. Stochastic Modelling of the Uncertain Parameters
In order to take into account the random variability of the uncertain parameters  (the Young’s modulus of the cancellous bone) and
(the Young’s modulus of the cancellous bone) and ![]() (the coefficient of friction between the cancellous bone and the femoral stem), these two parameters are modelled as continuous RVs, denoted
(the coefficient of friction between the cancellous bone and the femoral stem), these two parameters are modelled as continuous RVs, denoted  and
and  respectively.
respectively.
The continuous ![]() -valued random vector
-valued random vector 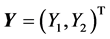 gathering these two scalar RVs is the probabilistic model of the uncertain vector parameter
gathering these two scalar RVs is the probabilistic model of the uncertain vector parameter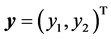 . In view of the intended numerical applications, this random vector is assumed to satisfy the following hypotheses:
. In view of the intended numerical applications, this random vector is assumed to satisfy the following hypotheses:
(H1) Its components  and
and 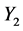 are independent.
are independent.
(H2) They both follow the same type of probability distribution.
(H3) Three types of probability distribution are admissible for these components: uniform, truncated Gaussian and truncated lognormal.
Concerning these hypotheses, we can make the following remarks:
(R1) Let![]() ,
, ![]() and
and ![]() be the probability density functions (pdf) of
be the probability density functions (pdf) of ,
,  and
and 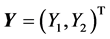 respectively. Then, from (H1):
respectively. Then, from (H1):![]() , that is,
, that is, :
:
![]() (27)
(27)
(R2) From (H2) and (H3) the densities ![]() and
and ![]() are both uniform, or truncated Gaussian or truncated lognormal.
are both uniform, or truncated Gaussian or truncated lognormal.
(R3) In connection with (H3), let ![]() be a scalar continuous RV with pdf
be a scalar continuous RV with pdf![]() . Then
. Then ![]() is said to follow:
is said to follow:
a) an uniform distribution with support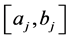 ,
,  , if:
, if:
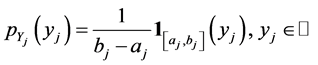 (28)
(28)
b) a truncated Gaussian distribution with mean![]() , standard deviation
, standard deviation ![]() and support
and support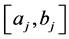 ,
,
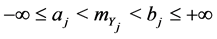 , if:
, if:
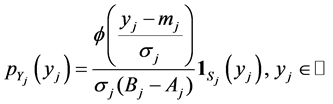 (29)
(29)
where ![]() is the indicator function of
is the indicator function of ![]() (i.e.
(i.e.
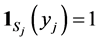 if
if 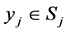 and
and  if
if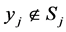 ),
),
![]() is the interval
is the interval ,
, 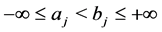 , and
, and![]() ,
, ![]() are the solutions of the nonlinear system:
are the solutions of the nonlinear system:
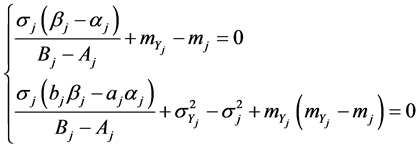 (30)
(30)
in which:

where ![]() and
and ![]() are respectively the one-dimensional standard Gaussian pdf and the one-dimensional standard Gaussian cumulative distribution function, such that:
are respectively the one-dimensional standard Gaussian pdf and the one-dimensional standard Gaussian cumulative distribution function, such that:
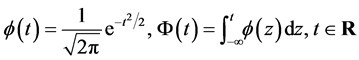 (31)
(31)
c) a truncated lognormal distribution with mean![]() , standard deviation
, standard deviation ![]() and support
and support ,
,
![]() , if:
, if:
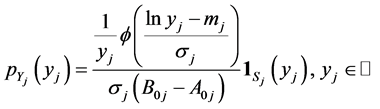 (32)
(32)
where ![]() is the interval
is the interval ,
, 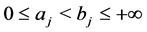 , and
, and![]() ,
, ![]() are the solutions of the nonlinear system:
are the solutions of the nonlinear system:
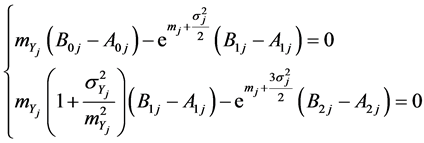 (33)
(33)
in which:
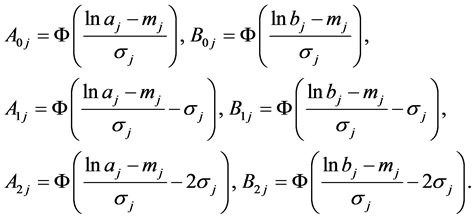
3.2. Safe and Failure Events
Equations (19) and (22) show that when the uncertain vector parameter  is modelled as a random vector
is modelled as a random vector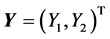 , the control variable
, the control variable  and the safety margin
and the safety margin , which depend on
, which depend on![]() , become scalar RVs. Let
, become scalar RVs. Let ![]() and
and ![]() be respectively these RVs. They are such that:
be respectively these RVs. They are such that:
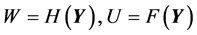 (34)
(34)
and are both defined on the probability space![]() .
.
Naturally, it is assumed here that the definition domains of ![]() and
and  (which are coincident according to Equation (22)) contain the support of the probability distribution of
(which are coincident according to Equation (22)) contain the support of the probability distribution of .
.
In this random context, the safe state and the failure state are defined by two events, the safe event  and the failure event
and the failure event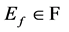 , such that:
, such that:
 (35)
(35)
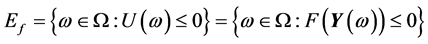 (36)
(36)
and which verify:
 (37)
(37)
Es is the event associated with the safe domain Ds and Ef is the event associated with the failure domain Df.
4. Reliability Analysis
4.1. Fundamental Objective
The fundamental objective of reliability analysis [19] is to calculate the probabilities that the events ![]() and
and  will occur, that is
will occur, that is ![]() and
and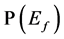 . These probabilities are given by:
. These probabilities are given by:
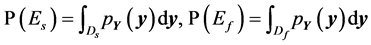 (38)
(38)
and, according to Equation (37), satisfy:
 (39)
(39)
where 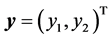 and
and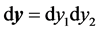 .
.
From Equation (39), ![]() is known as soon as
is known as soon as 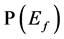 is known and vice versa. That is why in this work our attention is only focused on
is known and vice versa. That is why in this work our attention is only focused on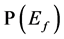 , called the failure probability and denoted
, called the failure probability and denoted ![]() in the following. This probability can be rewritten:
in the following. This probability can be rewritten:
 (40)
(40)
and its calculation requires the use of a numerical procedure. For the numerical applications treated in this study, we have chosen a Monte Carlo method ([19-21]).
4.2. Standard Formulation
In the classical reliability processes [19], it is customary to transform the initial formulation into a standard formulation in which the vector of random parameters follows a standard Gaussian distribution. This leads in our case to the construction of a regular transformation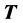 , with inverse
, with inverse![]() , such that the random vector
, such that the random vector 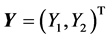 can be written:
can be written:
![]() (41)
(41)
where  is a
is a ![]() -valued standard Gaussian random vector defined on
-valued standard Gaussian random vector defined on![]() .
.
Once this transformation has been constructed, the failure event can be expressed in terms of ![]() as follows:
as follows:
 (42)
(42)
where  is a mapping from
is a mapping from ![]() into
into  such that,
such that,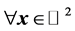 :
:
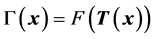 (43)
(43)
From Equation (32), the failure probability is then given by:
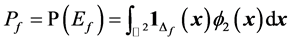 (44)
(44)
where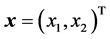 ,
, 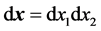 ,
,  is the subset of
is the subset of ![]() such that:
such that:
 (45)
(45)
And 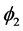 is the bidimensional standard Gaussian pdf, given by:
is the bidimensional standard Gaussian pdf, given by:
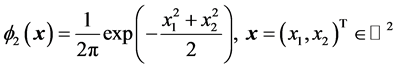 (46)
(46)
Note that Equation (44) can also be obtained by carrying out the variable change ![]() in Equation (40).
in Equation (40).
The set  is the failure domain in the standardized
is the failure domain in the standardized 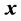 -space, that is in the space (identified with
-space, that is in the space (identified with![]() ) of the
) of the ![]() random vector’s realizations. Its complementary in
random vector’s realizations. Its complementary in![]() , that is the subset
, that is the subset
 , and the common boundary between
, and the common boundary between  and
and![]() , that is the curve
, that is the curve
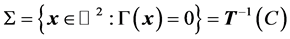 , are respectively the safe domain and the limit state curve in this standardized space (Figure 2).
, are respectively the safe domain and the limit state curve in this standardized space (Figure 2).
Equation (44) represents the standard formulation of the reliability problem. To estimate this integral, three Monte Carlo methods were used: the crude direct method and two more refined methods, based respectively on the importance sampling technique and the directional simulation technique ([19-21]).
Such a formulation is completely defined as soon as transformation 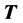 is known, and the latter only depends on the probability distribution of the random vector
is known, and the latter only depends on the probability distribution of the random vector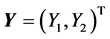 . As the components
. As the components  and
and  of
of 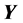 are assumed independent, this transformation is of the form:
are assumed independent, this transformation is of the form:
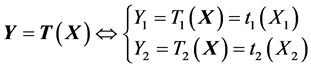 (47)
(47)
where![]() ,
, ![]() , is the
, is the ![]() -th coordinate of T and
-th coordinate of T and
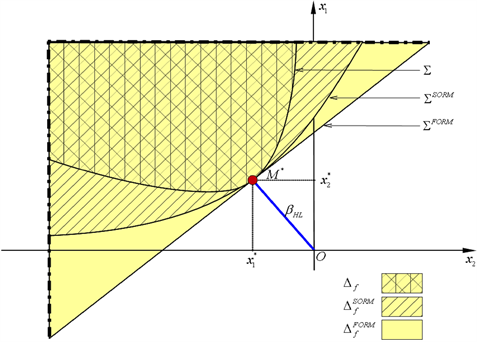
Figure 2. Geometric representation of the ![]() -point
-point![]() , of the failure domains
, of the failure domains , and of the limit state curves
, and of the limit state curves ![]() in the standardized x-space.
in the standardized x-space.
 ,
, ![]() , is a mapping from
, is a mapping from  into
into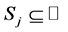 where
where ![]() is the definition domain of the pdf
is the definition domain of the pdf ![]() of
of![]() .
.
We give below the expression of transformation 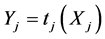 for each of the three distributions considered for
for each of the three distributions considered for ![]() (see Section 3.1, bearing in mind that
(see Section 3.1, bearing in mind that  and
and  are both assumed to follow the same type of probability distribution):
are both assumed to follow the same type of probability distribution):
a)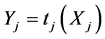 ,
, ![]() , follows a uniform distribution with support
, follows a uniform distribution with support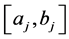 ,
, :
:
 (48)
(48)
b)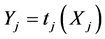 ,
, ![]() , follows a truncated Gaussian distribution with mean
, follows a truncated Gaussian distribution with mean![]() , standard deviation
, standard deviation ![]() and support
and support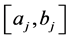 ,
,![]() :
:
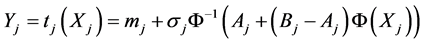 (49)
(49)
where  is the solution of the system (30).
is the solution of the system (30).
c)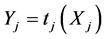 ,
, ![]() , follows a truncated lognormal distribution with mean
, follows a truncated lognormal distribution with mean![]() , standard deviation
, standard deviation ![]() and support
and support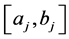 ,
,
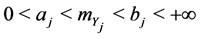 :
:
 (50)
(50)
where 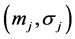 is the solution of the system (33).
is the solution of the system (33).
Note that the fact that 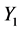 and
and 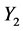 are both assumed to follow the same type of probability distribution is not a loss of generality. It is a simple working hypothesis, which could be changed without any incidence on the proposed methodology.
are both assumed to follow the same type of probability distribution is not a loss of generality. It is a simple working hypothesis, which could be changed without any incidence on the proposed methodology.
4.3. Hasofer-Lind Index
The Hasofer-Lind index ![]() ([19,22]) is a reliability indicator whose calculation is easier than that of failure probability
([19,22]) is a reliability indicator whose calculation is easier than that of failure probability![]() . It is defined in the standardized
. It is defined in the standardized 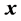 -space as follows:
-space as follows:
 (51)
(51)
where 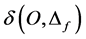 denotes the usual Euclidean distance between the origin point
denotes the usual Euclidean distance between the origin point ![]() and the failure domain
and the failure domain . Such an index is thus given by:
. Such an index is thus given by:
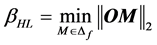 (52)
(52)
where ![]() denotes the canonical Euclidean norm on
denotes the canonical Euclidean norm on![]() .
.
The Rackwitz-Fiessler algorithm ([23,24]) is well suited to solving the constrained nonlinear optimization problem (52) and it was chosen to treat the numerical applications presented in Section 5. Note that for these applications the problem (52) has a unique solution. The solution point:
 (53)
(53)
such that , is called the design point, or
, is called the design point, or
![]() -point, and is located on the boundary
-point, and is located on the boundary  of
of 
(Figure 2). If 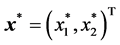 denotes the vector of
denotes the vector of ![]()
whose components ![]() and
and ![]() are the coordinates of
are the coordinates of ![]() (
( is the position vector of
is the position vector of![]() ), then
), then ![]() is given by:
is given by:
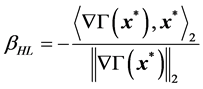 (54)
(54)
where  is the limit state function defined by Equation (43),
is the limit state function defined by Equation (43), ![]() is its gradient (assumed to exist at point
is its gradient (assumed to exist at point![]() ), and
), and ![]() is the canonical Euclidean inner product on
is the canonical Euclidean inner product on![]() .
.
4.4. FORM Approximation [19,22,23]
This approximation (FORM means First-Order Reliability Method) consists of replacing the failure domain 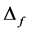 by the half-space:
by the half-space:
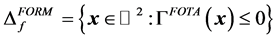 (55)
(55)
where ![]() is the First-Order Taylor Approximation of
is the First-Order Taylor Approximation of  at point
at point![]() , such that:
, such that:
 (56)
(56)
whose graph ![]() is a straight line tangent to
is a straight line tangent to  at
at ![]() (Figure 2).
(Figure 2).
The failure probability (44) is then approximated by:
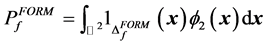 (57)
(57)
and a simple calculation gives:
![]() (58)
(58)
where ![]() is given by Equation (54).
is given by Equation (54).
4.5. SORM Approximation [19,24]
This approximation is a refinement of the previous method (SORM means Second-Order Reliability Method), which is based is based on the replacement of the failure domain 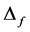 by the set:
by the set:
 (59)
(59)
where ![]() is the Second-Order Taylor Approximation of
is the Second-Order Taylor Approximation of  at point
at point![]() , that is the quadratic function given by:
, that is the quadratic function given by:
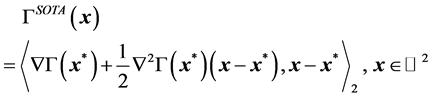 (60)
(60)
whose graph ![]() is a second-order curve tangent to
is a second-order curve tangent to 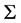 at
at ![]() (Figure 2). In Equation (60),
(Figure 2). In Equation (60), ![]() is the Hessian operator associated with
is the Hessian operator associated with 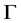 and is assumed to exist at point
and is assumed to exist at point![]() .
.
Using this substitution, the failure probability (44) is then approximated by:
 (61)
(61)
and this integral can be evaluated by using approximate formulas, such as the Breitung asymptotic formula [25]:
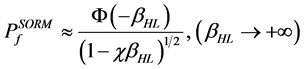 (62)
(62)
or the Hohenbichler asymptotic formula [26]:
 (63)
(63)
is an improvement of the previous one. In these formulas, ![]() is the curvature of the limit state curve
is the curvature of the limit state curve 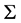 at
at![]() ,
, ![]() and
and ![]() are the functions given by Equations (31), and the following conditions are assumed to be verified:
are the functions given by Equations (31), and the following conditions are assumed to be verified: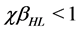 ,
,![]() .
.
5. Numerical Experiments
The numerical applications presented in this section concern the model of cementless hip prosthesis described in Section 2.1 and aim at estimating its reliability in various situations, either through the Hasofer-Lind index ![]() (calculated from the Rackwitz-Fiessler algorithm) or by means of the failure probability
(calculated from the Rackwitz-Fiessler algorithm) or by means of the failure probability ![]() (estimated from Monte Carlo simulations or by using the FORM and SORM approximations). All these methods have been implemented by the authors. We recall that the boneprosthesis system is considered as reliable if the Euclidean norm of the maximum relative displacement between the femoral stem and the cancellous bone do not exceed a given admissible value
(estimated from Monte Carlo simulations or by using the FORM and SORM approximations). All these methods have been implemented by the authors. We recall that the boneprosthesis system is considered as reliable if the Euclidean norm of the maximum relative displacement between the femoral stem and the cancellous bone do not exceed a given admissible value ![]() (the failure threshold).
(the failure threshold).
5.1. Influence of Probability Distributions and Scatterings
The purpose of this application is to highlight the influence of distributions and scatterings of random parameters on bone-prosthesis system reliability, expressed in terms of the Hasofer-Lind index![]() .
.
For this, 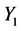 and
and 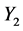 are assumed to be independent with fixed means
are assumed to be independent with fixed means 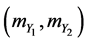 and variable coefficients of variation
and variable coefficients of variation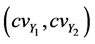 , and the three following cases are considered:
, and the three following cases are considered:
(C1) 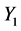 and
and 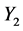 are uniformly distributed on the intervals
are uniformly distributed on the intervals ![]() and
and ![]() respectively(C2)
respectively(C2) 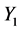 and
and 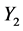 are truncated Gaussian with supports
are truncated Gaussian with supports ![]() and
and ![]() respectively(C3)
respectively(C3)  and
and  are truncated lognormal with supports
are truncated lognormal with supports ![]() and
and ![]() respectivelywhere in each case, for
respectivelywhere in each case, for![]() :
:
 (64)
(64)
The chosen values for![]() ,
, ![]() and the failure threshold
and the failure threshold ![]() are:
are:
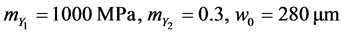 (65)
(65)
For the coefficients of variation ![]() and
and![]() , which quantify the scattering of
, which quantify the scattering of 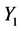 and
and  respectively, three values are considered in each
respectively, three values are considered in each ![]() case according to the following strategy:
case according to the following strategy:
1) ![]() is fixed to its reference value
is fixed to its reference value ![]() and
and ![]() successively takes the values
successively takes the values![]() ,
, ![]() ,
,![]() ;
;
2) ![]() is fixed to its reference value
is fixed to its reference value ![]() and
and ![]() successively takes the values
successively takes the values![]() ,
, ![]() ,
,![]() .
.
The results obtained are summarized in Table1 In each case, we can see the significant effect of the coefficients of variation on the index![]() . We can also observe that the effect of
. We can also observe that the effect of ![]() (coefficient of variation of the coefficient of friction) is greater than that of
(coefficient of variation of the coefficient of friction) is greater than that of ![]() (coefficient of variation of the Young’s modulus of the cancellous bone). Finally, we can point out that the probability distributions of
(coefficient of variation of the Young’s modulus of the cancellous bone). Finally, we can point out that the probability distributions of  and
and  have a minor influence on
have a minor influence on![]() .
.
5.2. Influence of Truncation Lengths
In this application, the random parameters  and
and 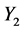 are assumed to be independent and distributed according to truncated distributions with variable supports and constant first two moments. Under this assumption, the objective is to evaluate the effect of the support length of each distribution (so-called truncation length) on the reliability of the hip prosthesis expressed in terms of the Hasofer-Lind index
are assumed to be independent and distributed according to truncated distributions with variable supports and constant first two moments. Under this assumption, the objective is to evaluate the effect of the support length of each distribution (so-called truncation length) on the reliability of the hip prosthesis expressed in terms of the Hasofer-Lind index![]() .
.
The supports ![]() and
and ![]() of the distribution of
of the distribution of 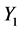 and
and  are chosen of the form:
are chosen of the form:
![]() (66)
(66)
where ![]() and
and ![]() are strictly positive non-dimensional coefficients controlling the length of the supports. To highlight their influence on
are strictly positive non-dimensional coefficients controlling the length of the supports. To highlight their influence on![]() , four situations are considered:
, four situations are considered:
(TG1) 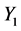 and
and  are truncated Gaussian,
are truncated Gaussian, 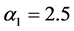 and α2 successively takes the values
and α2 successively takes the values ,
, ![]() and
and![]() (TG2)
(TG2) 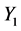 and
and  are truncated Gaussian,
are truncated Gaussian, 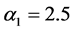 and
and ![]() successively takes the values
successively takes the values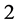 ,
, ![]() and
and![]() (TLN1)
(TLN1)  and
and 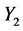 are truncated lognormal, α2 = 2.5 and
are truncated lognormal, α2 = 2.5 and ![]() successively takes the values
successively takes the values ,
, ![]() and
and![]() (TLN2)
(TLN2)  and
and 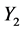 are truncated lognormal, α1 = 2.5 and
are truncated lognormal, α1 = 2.5 and ![]() successively takes the values
successively takes the values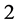 ,
, ![]() and
and![]() .
.
The chosen values for the statistics , j = 1,2and the failure threshold
, j = 1,2and the failure threshold ![]() are the following:
are the following:
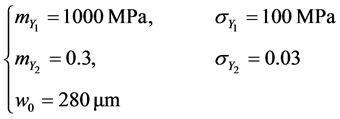 (67)
(67)
The results obtained are listed in Table2 First we can see that the behaviour of ![]() with respect to the truncation lengths depends on the nature of the considered probability distributions. Indeed, in the truncated Gaussian case this behaviour is non-monotonous (
with respect to the truncation lengths depends on the nature of the considered probability distributions. Indeed, in the truncated Gaussian case this behaviour is non-monotonous (![]() decreases then increases) in each considered situation (TG1 and TG2), while in the truncated lognormal case, it is either increasing monotonous (situation TLN1) or decreasing monotonous (situation TLN2). In each case, however, the influence of the truncation lengths on
decreases then increases) in each considered situation (TG1 and TG2), while in the truncated lognormal case, it is either increasing monotonous (situation TLN1) or decreasing monotonous (situation TLN2). In each case, however, the influence of the truncation lengths on ![]() is not very significant.
is not very significant.
Table 1. Influence of the probability distribution and of the coefficients of variation of ![]() and
and ![]() on the Hasofer-Lind index
on the Hasofer-Lind index![]() .
.
Table 2. Influence of truncation lengths on ![]() in the truncated Gaussian case (i.e.
in the truncated Gaussian case (i.e. ![]() and
and ![]() truncated Gaussian) and in the truncated lognormal case (i.e.
truncated Gaussian) and in the truncated lognormal case (i.e. ![]() and
and ![]() truncated lognormal).
truncated lognormal).
5.3. Influence of the Failure Threshold
In this section, we study the influence of the failure threshold ![]() on the reliability of the prosthesis, again using the Hasofer-Lind index
on the reliability of the prosthesis, again using the Hasofer-Lind index ![]() as a reliability indicator.
as a reliability indicator.
To this end, the random parameters  and
and 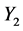 are assumed to be independent and uniformly distributed with means and standard deviations given by Equation (67); five values are successively considered for the failure threshold
are assumed to be independent and uniformly distributed with means and standard deviations given by Equation (67); five values are successively considered for the failure threshold ![]() (in
(in![]() ): 270, 275, 28 0, 285, 290.
): 270, 275, 28 0, 285, 290.
The obtained values of ![]() are given in Table 3 which also contains, for information, the corresponding values for the FORM approximation
are given in Table 3 which also contains, for information, the corresponding values for the FORM approximation ![]() of failure probability, given by Equation (58).
of failure probability, given by Equation (58).
We can first observe that the values of ![]() are quite low for all the considered values of
are quite low for all the considered values of![]() , which are nevertheless common values for this threshold. This comes quite obviously from the chosen values for the coefficients of variation of
, which are nevertheless common values for this threshold. This comes quite obviously from the chosen values for the coefficients of variation of 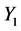 and
and , which are relatively high
, which are relatively high . We can also underline that these results are logical in the sense that
. We can also underline that these results are logical in the sense that ![]() increases as
increases as ![]() increases. It is interesting, moreover, to note that this increase is quasi-linear over the range of the considered
increases. It is interesting, moreover, to note that this increase is quasi-linear over the range of the considered ![]() values.
values.
5.4. Comparison of Various Approximations of Pf
In this application we consider the same example as in the previous application (see Section 5.3), and for each value of the failure threshold ![]() we compare the FORM and SORM approximations
we compare the FORM and SORM approximations ![]() and
and ![]() of
of ![]() (given by Equations (58) and (63) respectively) with the target value of this probability, obtained by using the crude Monte Carlo method taken as the reference method.
(given by Equations (58) and (63) respectively) with the target value of this probability, obtained by using the crude Monte Carlo method taken as the reference method.
Estimating ![]() from the latter requires here the simulation of
from the latter requires here the simulation of 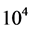 realizations
realizations
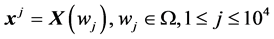 , of the standard Gaussian vector
, of the standard Gaussian vector![]() , then, for each simulated realization
, then, for each simulated realization![]() , the calculation of the corresponding value
, the calculation of the corresponding value  of the limit state function
of the limit state function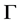 . Such an estimation requires thus
. Such an estimation requires thus 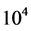 finite element calculations. This is why two other less expensive Monte Carlo methods were used: one based on the importance sampling (IS) technique, the other on the directional simulation (DS) technique ([19- 21]).
finite element calculations. This is why two other less expensive Monte Carlo methods were used: one based on the importance sampling (IS) technique, the other on the directional simulation (DS) technique ([19- 21]).
The values of ![]() given by these two improved Monte Carlo methods and by the crude Monte Carlo method are respectively denoted
given by these two improved Monte Carlo methods and by the crude Monte Carlo method are respectively denoted![]() ,
, ![]() and
and![]() . The comparison of
. The comparison of ![]() and
and ![]() with
with ![]() is shown in Table4 Table 5 gives, for
is shown in Table4 Table 5 gives, for , the number of finite element calculations required by the Monte Carlo methods based on the IS and DS techniques to provide the same value for
, the number of finite element calculations required by the Monte Carlo methods based on the IS and DS techniques to provide the same value for ![]() as that given by the crude Monte Carlo method (i.e.
as that given by the crude Monte Carlo method (i.e.![]() ).
).
The results obtained show first that ![]() and
and ![]() are poor approximations of
are poor approximations of![]() . They also show that
. They also show that ![]() is not a significant improvement on
is not a significant improvement on![]() . This can be explained by the fact that the local approximations
. This can be explained by the fact that the local approximations ![]() and
and ![]() of the limit state curve
of the limit state curve 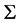 (Figure 2) are not accurate enough to adequately represent
(Figure 2) are not accurate enough to adequately represent 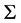 in a sufficiently large neighbourhood of the design point
in a sufficiently large neighbourhood of the design point![]() . The results in Table 5 confirm that the Monte Carlo methods based on the IS and DS techniques are more efficient than the crude Monte Carlo method. We can also observe that the method based on the DS technique is less time-consuming, and therefore more efficient, than the one based on the IS technique.
. The results in Table 5 confirm that the Monte Carlo methods based on the IS and DS techniques are more efficient than the crude Monte Carlo method. We can also observe that the method based on the DS technique is less time-consuming, and therefore more efficient, than the one based on the IS technique.
Table 3. Influence of the failure threshold on the HasoferLind index ![]() and on the associated FORM approximation
and on the associated FORM approximation 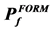 of
of .
.
Table 5. Number of finite element (FE) calculations required by the Monte Carlo methods based on the IS and DS techniques to provide the same value for  as that given by the crude method.
as that given by the crude method.
6. Conclusions
The aim of this paper was to present a methodology to enable the prediction in a probabilistic context of the primary stability of cementless hip prostheses in the presence of uncertainties. Based on a reliability approach, this methodology supposes the numerical model describing the mechanical behaviour of the prosthesis-cancellous bone couple, the probabilistic models of uncertain parameters and the failure criterion expressing the loss of stability of the prosthesis to be known. The underlying mechanical problem is a classical problem of contact with friction between two three-dimensional deformable bodies: a Depuy Corail® prosthesis is implanted without cement in a femur. This problem is solved using a finite element model based on Bathe’s formulation. Due to their variability in the literature, we chose to consider the Young’s modulus of the cancellous bone and the coefficient of friction between the cancellous bone and the femoral stem as uncertain parameters. They were modelled as random variables, assumed successively to be uniform, truncated Gaussian and truncated lognormal. Finally, failure was defined as the exceeding of a given limit value by the maximum relative displacement between the femoral stem and the cancellous bone. The reliability of the coupled system was estimated using two indicators: the Hasofer-Lind index and the failure probability. The first was calculated using the RackwitzFiessler optimization algorithm. The second was estimated first by using approximate formulas derived from FORM and SORM approaches, then by means of three Monte Carlo methods: the crude Monte Carlo method, the method based on the importance sampling technique and that based on the directional simulation technique.
The presented numerical applications have shown the relevance of the proposed methodology and given an indication of its great potential in the field of prosthesis reliability. A different failure criterion could be envisaged, such as the acceptable maximum stress or the optimization of the contact area, for instance.
This methodology has been presented in the case where only two parameters are uncertain. It is clear, however, that its validity and its operational capacity would not be compromised by an increase in the number of uncertain parameters. This personal probabilistic model enables clinicians to compare the primary stability of cementless prostheses, and to choose the optimal implant design while taking into account uncertainties in the model input data.
Acknowledgements
This work was financially supported by the Conseil Général de l’Allier and Society DePuy France.
REFERENCES
- R. Pilliar, J. Lee and C. Maniatopoulos, “Observation of the Effect of Movement on Bown Ingrowth into Porous-Surfaced Implants,” Clinical Orthopaedics and Related Research, 1986, pp. 108-113.
- A. Wong, A. New, G. Isaacs, and M. Taylor, “Effect of bone material properties on the initial stability of a cementless hip stem : a finite element study,” Proc. IMechE Part H : Journal of Engineering in Medicine, IMechE Part H : Journal of Engineering in Medicine,
- M. Viceconti, G. Brusi, A. Pancanti and L. Cristofolini, “Primary Stability of an Anatomical Hip Stem: A Statistical Analysis,” Journal of Biomechanics, Vol. 39, No. 7, 2006, pp. 1169-1179. http://dx.doi.org/10.1016/j.jbiomech.2005.03.024
- M. A. Perez, J. Grasa, J. Garcia-Aznar, J. A. Bea and M. Doblare, “Probalistic Analysis of the Influence of the Bondinf Degree of the Stem-Cement Interface in the Performance of Cemented Hip Prostheses,” Journal of Biomechanics, Vol. 39, No. 10, 2006, pp. 1859-1872. http://dx.doi.org/10.1016/j.jbiomech.2005.05.025
- S. K. Easley, S. Pal and P. R. Tomaszewski, A. J. Petrella, P. J. Rullkoetter and P. J. Laz, “Finite Element-Based Probalistic Analysis Tool for Orthopaedic Applications,” Computer Methods and Programs in Biomedecine, Vol. 85, No. 1, 2007, pp. 32-40. http://dx.doi.org/10.1016/j.cmpb.2006.09.013
- O. Kayabasi and B. Ekici, “Probalistic Design of a Newly Designed Cemented Hip Prostheses Using Finite Element Method,” Materials and Design, Vol. 29, No. 5, 2008, pp. 963-971. http://dx.doi.org/10.1016/j.matdes.2007.03.024
- C. Dopico-Gonzalez, A. M. New and M. Browne, “Probalistic Analysis of an Uncemented Total Hip Replacement,” Medical Engineering & Physics, Vol. 31, No. 4, 2009, pp. 470-476. http://dx.doi.org/10.1016/j.medengphy.2009.01.002
- C. K. Fitzpatrick, M. A. Baldwin, P. J. Rullkoetter and P. J. Laz, “Combined Probabilistic and Principal Component Analysis Approach for Multivariate Sensitivity Evaluation and Application to Patellofemoral Mechanics,” Journal of Biomechanics, Vol. 44, No. 1, 2011, pp. 13-21. http://dx.doi.org/10.1016/j.jbiomech.2010.08.016
- M. Browne, R. Langley and P. Gregson, “Reliability Theory for Load Bearing Biomedical Implants,” Biomaterials, Vol. 20, No. 14, 1999, pp. 1295-1292. http://dx.doi.org/10.1016/S0142-9612(99)00027-7
- F. Dar, J. Meakin and R. Aspden, “Statistical Methods in Finite Element Analysis,” Journal of Biomechanics, Vol. 35, No. 9, 2002, pp. 1155-1161. http://dx.doi.org/10.1016/S0021-9290(02)00085-4
- D. P. Nicolella, B. H. Thacker, H. Katoozian and D. T. Davy, “The Effect of Three-Dimensional Shape Optimization on the Probabilistic Response of a Cemented Femoral Hip Prosthesis,” Journal of Biomechanics, Vol. 39, No. 7, 2006, pp. 1265-1278. http://dx.doi.org/10.1016/j.jbiomech.2005.03.010
- M. Bah and M. Browne, “Failure of the cement mantel in hip implants : a probabilistic approach,” Transactions of the 50th Annual Meeting of the Orthopaedic Research Society, 2004, p. 1430.
- C. Dopico-Gonzalez, A. M. New and M. Browne, “Probalistic Analysis of the Uncemented Hip Replacement— Effect of Femur Characteristics and Implant Design Geometry. Journal of Biomechanics, Vol. 43, No. 3, 2010. pp. 512-520. http://dx.doi.org/10.1016/j.jbiomech.2009.09.039
- M. T. Bah and P. B. Nair, M. Taylor and M. Browne, “Efficient Computational Method for Assessing the Effects of Implant Positioning in Cementless Total Hip Replacement,” Journal of Biomechanics, Vol. 44, No. 7, 2011, pp. 1417-1422. http://dx.doi.org/10.1016/j.jbiomech.2010.12.027
- K. J. Bathe and P. A. Bouzinov, “On the Constraint Function Method for Contact Problems.” Computers & Structures, Vol. 64, No. 5-6, 1997, pp. 1069-1085. http://dx.doi.org/10.1016/S0045-7949(97)00036-9
- K. J. Bathe, “Finite Element Procedures,” Prentice-Hall, Englewood Cliffs, 1995.
- UGSCorp, “NX Nastran® Advanced Nonlinear Theory and Modeling Guide,” National Aeronautics and Space Administration, 2007.
- X. S. Hu, F. Labesse-Jied, G. Demey, and T. A. S. Selmi, “The primary stability of cementless implants - experimental and finite element studies,” in 16th Congress of the European Society of Biomechanics (ESB 2008), (Lucerne (Switzerland)), July 6-9 2008.
- O. Ditlevsen and H. O. Madsen, “Structural Reliability methods,” John Wiley & Sons, Hoboken, 1996.
- G. S. Fishman, “Monte Carlo: Concepts, Algorithms and Applications,” Springer-Verlag, New York, 1996.
- R. Y. Rubinstein and D. P. Kroese, “Simulation and the Monte Carlo Method,” Wiley, Hoboken, 2008.
- A. M. Hasofer and M. C. Lind, “An Exact and Invariant First Order Reliability Format,” Journal of Engineering Mechanics, Vol. 100, 1974, pp. 111-121.
- R. Rackwitz, “Practical Probabilistic Approach to Design first Order Reliability Concepts for Design Codes,” Bulletin d’Information de CEB, Vol. 112, 1976.
- B. Fiessler, H. J. Neumann and R. Rackwitz, “Quadratic Limit States in Structural Reliability,” Journal of Engineering Mechanics, Vol. 105, 1979, pp. 661-678.
- K. Breitung, “Asymptotic Approximations for Multinormal Integrals,” Journal of Engineering Mechanics, Vol. 110, No. 3, 1984, pp. 357-366. http://dx.doi.org/10.1061/(ASCE)0733-9399(1984)110:3(357)
- M. Hohenbichler and S. Gollwitzer and W. Kruse and R. Rackwitz. New light on Firstand Second-Order Reliability Methods. Structural Safety, Vol. 4, No. 4, 1987, pp. 267-284



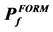 ,
, 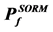 and
and 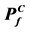 for each failure threshold value
for each failure threshold value