World Journal of Mechanics
Vol.3 No.6(2013), Article ID:36844,7 pages DOI:10.4236/wjm.2013.36028
Role on Moment of Inertia and Vortex Dynamics for a Thin Rotating Plate
Faculty of Science and Engineering, Toyo University, Saitama, Japan
Email: kubota548@toyo.jp
Copyright © 2013 Yoshihiro Kubota, Osamu Mochizuki. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Received June 27, 2013; revised July 29, 2013; accepted August 25, 2013
Keywords: Autorotation; Thin Rotating Plate; Free Flight; Moment of Inertia; Visualization; PIV
ABSTRACT
In this study, we focused on the lift generation with a thin rotating plate. The objective of this study is to understand the appropriate shape and the role of vortex for rotating thin plate. We determined the shape of the plate through free-flight tests of paper strips and investigated the aerodynamic characteristics of the rotating plate with the selected shape. The rectangular plate with an aspect ratio 7 was relevant from moment of inertia and bending stress. An endplate on a wing tip increased the stability on the lateral vortex structure behind the rotating plate. Velocity field measurement by Particle Image Velocimetry (PIV) showed that the lift force was generated twice in a rotating cycle.
1. Introduction
The aerodynamics of freely falling paper plate such as business cards was studied to understand for the fluttering or the tumbling. The purpose of this study is to understand the appropriate shape of plate, and the role of vortex to fly or glide the longer distance with a rotating thin plate. We are focusing on the aerodynamic characteristics of autorotation of thin paper plate. The autorotation is free to rotate with a fixed axis of a centroid of paper plate. The motion of paper plate during the autorotation is not only vertically but also horizontally. Moreover, the horizontal motion is not periodic oscillating motion like a swing motion. This means that the paper plate has the direction of a horizontal displacement. Mittal et al. showed that the paper plate during the autorotation generates the lift force [1]. So that if we controlled rotation of paper plate certainly to generate the enough lift force during the autorotation. This might become a small flier such a Micro Air Vehicle (MAV) [2]. This is a starting point of our study.
From the previous study, the aerodynamics of freely falling paper plate was known with the fluttering, the tumbling, and the autorotation. The experimental study on the frequency of tumbling plate was studied by Mahadevan et al. [3]. They concluded that the tumbling frequency was associated with the cross-sectional shape of plate as the chord length of paper and the thickness of paper. The increasing of frequency occurred with squared root of thickness. Hirata et al. reported the experimental study of an aerodynamic characteristics of tumbling plate [4]. They studied the relation among inertia moment, rotation, lift coefficient, and drag coefficient of paper as aerodynamic characteristics. Their results proposed the empirical formulation of aerodynamic characteristics from a function of Reynolds number.
From the numerical approach, Andersen et al. showed the numerical study of relation between the moment of inertia by the shape of plate and the transition between fluttering and tumbling [5]. Also, they reported both a comparison between numerical and an experimental studies. The experimental results indicated the transition between fluttering and tumbling was caused with the increasing thickness of paper. Pesavento et al. were studied the aerodynamic lift during a tumbling [6]. They were shown that an aerodynamic lift on a tumbling plate was dominated by the both falling velocity and angular velocity of stiff paper plate such as the business card. An influence of cross sectional shape for freely falling paper was studied numerically by Jin C. et al. [7]. The main difference with a cross sectional shape was angular velocity. For a tumbling, angular velocity dominates the lift force by Pesavento et al. [6], so that the shape for falling paper plate was needed to be considered for autorotation.
The main scope of our study is the shape of paper, and the stability during the autorotating plate. The influence of shape was focusing on the influence of inertia moment of paper, since the larger moment of inertia causes the difficulty of rotation. Since, the rotation of paper plate is key subject of autorotation. In addition, the starting point of this study is to understand the generation of lift force with an autorotation for a small flier, thus the stability of autorotation is necessary to studied. The influence of endplates of rotating wing was studied for the improvement of aerodynamic stability.
We determined the aspect ratio of the plate by using a falling paper and observed that a plate with an aspect ratio of 7 achieved the longest flight distance, which means it must have the highest lift/drag ratio. Next, we tested the stability performance with a thin auto rotating plate with an aspect ratio of 7. We employed particle image velocimetry (PIV) to the investigate vortex formation around the rotating plate. In addition, we discuss herein the relation between the flight performance and the shape of wing.
2. Experimental Apparatus and Method
We performed three different experiments: 1) free-flight tests with paper strips of varying shapes and a test model with an autorotating thin plate; 2) flow visualization near the tip of a rotating plate; 3) PIV measurements of vortices produced by the rotating plate.
To select the shape of the rotating plate that will be used in the test model, we checked the free-flight performance of paper strips with different shapes, as shown in Figure 1. The strips shown in Figure 1(a) have the same aspect ratio, which is defined as the ratio of the spanwise length to the chord length at the tip of the plate. The strips shown in Figure 1(b) have the same area but
 (a) (b)
(a) (b)
Figure 1. Different shapes of paper strips. (a) Identical aspect ratio, but different chord length at the center position; (b) Identical area, but different aspect ratio. Weights of A1, A2, and A3 are 0.038, 0.049, and 0.064 g, respectively. Dimensions are in mm.
different aspect ratio and are all made of paper.
The test model shown in Figure 2, which had a thin plate rotating about its spanwise axis, was used to observe flight performances. The size of the plate, which served as a rotating wing, was 20 mm along the chord and 70 mm in the spanwise direction. Thus, the total aspect ratio of the two plates aligned on each side of the center sphere was 7. The center spherical body made from styrene foam was 30 mm in diameter. The total weight of the model was 30 g. Future plans include transforming the spherical body into a fuselage in which a motor, actuators, sensors, and a tiny camera are packed. The photograph in Figure 2(b) shows the test model with end plates affixed at both tips of the plate.
An experimenter threw the test model with paper strips in the forward direction by hand, releasing it 2 m above the floor. Once released, the model fell freely. A 0.25 × 0.25 m2 square grid was drawn in an area of 5 × 5 m2 on the floor to record the landing point of the test model. The averaged falling speed was 1.3 m/s. Thus, based on the speed and chord length, the Reynolds number was 1.7 × 103. The spin parameter, which we define later, was 0.4. To check the effects of the end plates (attached at the plate tips) on flight performance, the test model with end plates (as seen in Figure 2) was flight-tested under conditions similar to those for the model without the end plates. Five hundred flight tests were conducted for one model in a room with no flow (i.e., no air conditioner). The experimenter started the flight tests after practicing the model throw so as to minimize the influence of the launch on the experimental results.
We investigated the three-dimensional effects of the finite plate by visualizing the fluid flow using a dye in a circulating open water channel as shown in Figure 3. The plate immersed in the water had a chord length of 40 mm and spanwise length of 180 mm. Revolutions of the plate were controlled by a motor to change the peripheral speed of the plate relative to the main flow velocity. The ratio of the peripheral speed of the plate to the main flow velocity is called the spin parameter S and is defined as
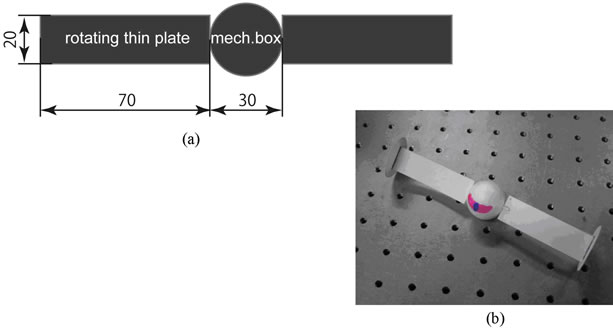
Figure 2. Test model. (a) Schematic with dimensions in mm; (b) photograph of test model with end plates on left and right extremities.
follows:
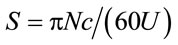 (1)
(1)
Here N represents the revolutions per minute of the rotating plate, c is the plate chord length, and U is the main stream velocity. The main stream velocity was 0.1 m/s in the water channel experiment. Based on the chord length and main stream velocity, the Reynolds number was 4 × 103. We visualized the flow near the wing tip by using a dye injected upstream of the rotating wing and recorded streak-line interactions by a high-speed camera. Vortex formation around the rotating wing and velocity fields were observed by PIV. Particles 100 mm in diameter were used to detect velocity fields.
3. Results and Discussion
3.1. Free-Flight Test
Figure 4 shows the relationship between the flying time and moment of inertia about the spanwise axis of the paper strips shown in Figure 1. The paper strips shown in Figure 1(b) have the same area but different moments of inertia. In this case, the strip with a smaller moment of inertia flies longer, as seen in Figure 4. Since the strip with the smaller moment of inertia rotates more easily, this result indicates that the rotation speed is responsible for long flight times.
On the other hand, the strips shown in Figure 1(a) have the same aspect ratio but different chord lengths at the center position. Although the moment of inertia of strip A7 is small, its flight time is short. Furthermore, the decreasing of chord length at the center caused the bending of wing easily from the observation. Since, the maximum bending stress increased with the decreasing of
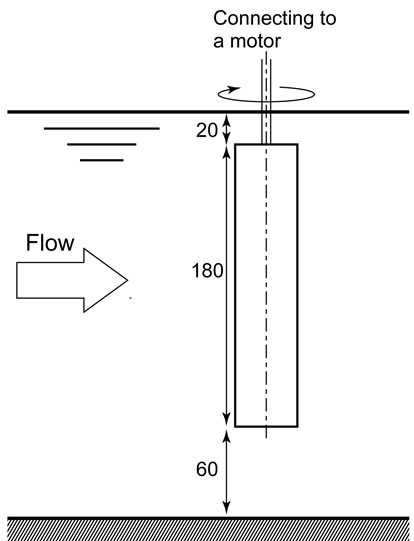
Figure 3. Experimental setup for dye visualization and water-tunnel PIV measurements. Dimensions are in mm.
chord length at the center. As a result, the rectangular paper has the longest flight time. Therefore, the suitable shape of plate for autorotation is the rectangular as the flier. For the model test, the rectangular wing was used.
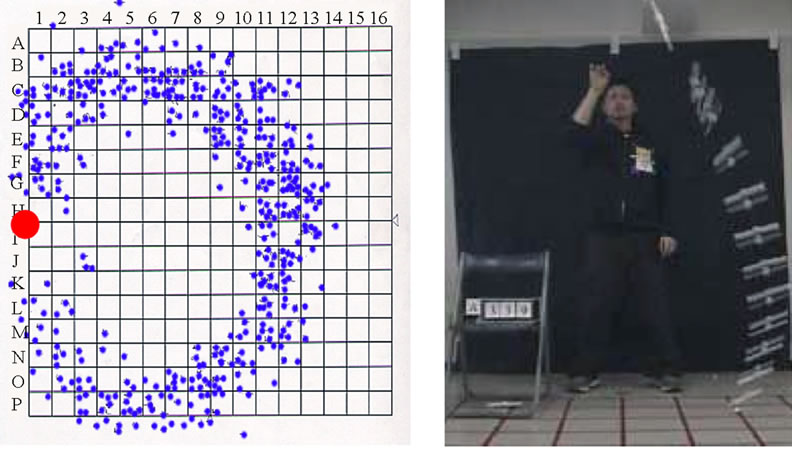
Figure 5 shows the distribution in landing position for the model plane without end plates that is shown in Figure 2. The flight locus of the model plane is always spiral in this case, as shown in the photograph in Figure 5. The model plane tilts just after being launched, and this tilt angle is unpredictable, making it difficult to predict the landing position. Thus, the landing positions are distributed around the circumference of a circular strip, as seen in Figure 5. The maximum distance between the launch and landing position is approximately 2.7 m. We consider the flight to be strongly influenced by small disturbances caused by a tip vortex.
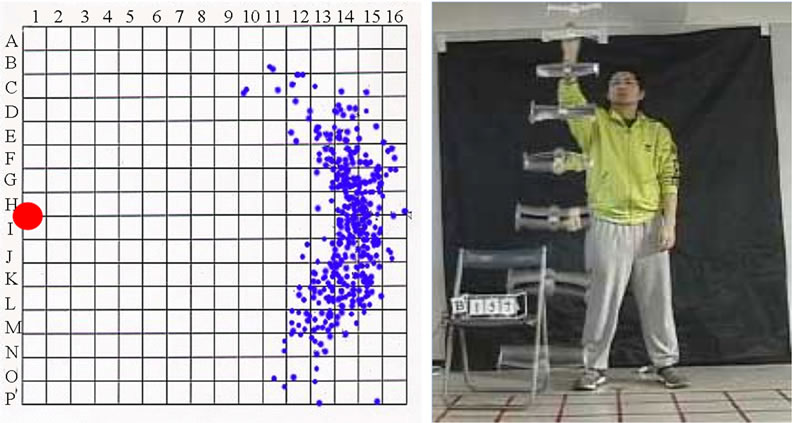
Then, we attached end plates at both tips of the plate, as shown in the photograph in Figure 2. The end plate of a fixed wing reduces the induced drag by preventing interaction between the flow along the upper and lower surfaces of the wing. The landing positions of the model plane with end plates are converged into a small area in front of the launch position, as shown in Figure 6. Thus, the model plane with end plates flies straight forward, as seen in the photograph in Figure 6.
Since the experimental conditions (except for the end plates and throwing manner) are similar to those in the previous experiment, the difference in flight paths is attributed to the effect of the end plates. This shows that the end plate is effective in stabilizing the flight of the model plane. Since the pressure distribution on the wing surface is influenced by lateral vortices generated from
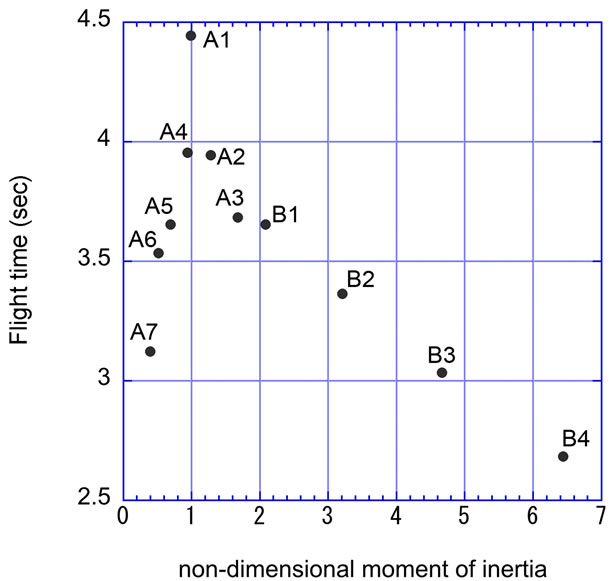
Figure 4. Flying time plotted versus moment of inertia of paper strips. Each label corresponds to those shown in Figure 1.
 (a) (b)
(a) (b)
Figure 5. Distribution in the landing position (a) and typical flight (b) path for model plane without end plates.
 (a) (b)
(a) (b)
Figure 6. Distribution in the landing position (a) and typical flight path (b) for model plane with end plates.
the edge of the rotating plate, the interactions between the tip of the vortex and lateral vortex affect aerodynamic forces, which in turn affect the flight of the model plane. Thus, the end plates cut the cross talk between the upper and lower surfaces of the wings. In fact, end plates are well known to reduce the induced drag. The use of end plates avoids the uncertainty caused by the three-dimensional deformation of the connected vortex at the wing edge, which facilitates stable flight.
3.2. Flow Visualization near Plate Tip
To observe the effects of the end plate, flows near the tip of the main plate were observed using a dye. Figure 7 compares the streak lines near the main plate tip for a plate with and without an end plate. The streak lines shown in Figure 7(a) (without end plate) are entangled behind the plate, which indicates that the flow behind a rotating plate is disturbed by the trailing vortex near the tip. A lateral vortex separated from the forward edge of the rotating plate is easily affected by this disturbance.
The distribution of the surface pressure induced by the separated vortices must be different at both tips. Thus, the lift forces on both tips are not balanced; thus, the model plane tilts if there are no end plates. In contrast, the streak lines near the tip of the plate with the end plate are laminar, as seen in Figure 7(b). This shows that the end plate is useful for stabilizing the lateral vortex structure behind the rotating plate. Thus, the model plane with the end plates has balanced lift forces, and thus, it flies straight, as seen in the photograph in Figure 6.
3.3. PIV Measurements near Rotating Plate
With PIV, we observed lateral vortices at the leading and trailing edges of the rotating plate. To investigate the temporal evolution of lateral vortices, we captured the flow field at phase steps of π/4, which was accomplished with a high-speed camera and a double-pulse-laser-light sheet that detected the flow field during the rotation of the plate in an open water channel. The flow fields were averaged at each phase. The temporal evolution of the
 (a) (b)
(a) (b)
Figure 7. Streak lines near the tip of a rotating plate (a) without an end plate and (b) with an end plate.
flow field in the middle section of the rotating plate (without the end plate) is shown in Figure 8 for S = 0.6 and 1.0. The velocity vectors and stream lines are visible in Figure 8 and show the formation of a lateral vortex behind the rotating plate. The vectors are color coded according to speed. Time progresses from the left panel to the right. The time interval between each figure corresponds to a π/4 phase step in one revolution cycle. The labels A and B at the plate edges identify the edges during a revolution. The edge moves backward, and the relative velocity of the edge with respect to the main flow velocity is small when S < 1. The B edge moves forward, and the relative velocity of the edge with respect to the main flow velocity is always large. The changes in circulation generated at the A and B edges are estimated over an angular range 0 < ωt < π by the following relationships:
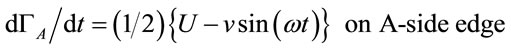 (2)
(2)
 (3)
(3)
Here ω is an angular speed, and v defined by 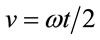 is the linear speed at the edge of the rotating plate. The term U ± v sin(ωt) represents the relative flow speed at each edge. From ωt = 0 to π, the change in the circulation of vortices shed from the A edge is smaller than that from the B edge. The change in the flow field during half a rotation is also shown in Figure 8 (the flow field is the same for the other half cycle). The flow field at S = 0.6 was obtained in a manner similar to that previously discussed for S = 1. The strong lateral vortex seen in the top-left panel of Figure 8 is shed from the B edge during the previous half turn. The strong vortex is located below the B edge and rotates counterclockwise (ccw). This vortex is regarded as a starting vortex of a wing that moves suddenly. As a result, the rotation of the plate deflects the mean flow downward, which generates lift.
is the linear speed at the edge of the rotating plate. The term U ± v sin(ωt) represents the relative flow speed at each edge. From ωt = 0 to π, the change in the circulation of vortices shed from the A edge is smaller than that from the B edge. The change in the flow field during half a rotation is also shown in Figure 8 (the flow field is the same for the other half cycle). The flow field at S = 0.6 was obtained in a manner similar to that previously discussed for S = 1. The strong lateral vortex seen in the top-left panel of Figure 8 is shed from the B edge during the previous half turn. The strong vortex is located below the B edge and rotates counterclockwise (ccw). This vortex is regarded as a starting vortex of a wing that moves suddenly. As a result, the rotation of the plate deflects the mean flow downward, which generates lift.
In contrast to the strong vortex, the weak lateral vortex is shed from the A edge and rotates in clockwise (cw). The weak vortex seen in the top-left panel of Figure 8 is shed from the A edge during the previous half turn and is located near the B edge at ωt = 0. Since the small vortex travels near the upper surface of the plate until it is shed from the A edge, we speculates that it affects the pressure on the upper surface of the plate while the plate rotates. The shedding frequency of these vortices is two times the rotation frequency. Mochizuki et al. (1987) analyzed aerodynamic characteristics with an impulsively rotated plate. They showed that the generation of lift force was caused twice in a rotating cycle with a plate rotated on a center of axis. Thus, the lift force is generated two times per rotation.
The change in flow patterns at S = 1.0 is shown in the bottom row of Figure 8. By comparing figures for S = 1.0 at a given phase with those for S = 0.6 at the same phase, we obtain the effects of the rotation speed on vortex formation. For S = 1.0, the peripheral velocity of the backward-moving edge (i.e., the A edge) of the plate is equal to the main stream velocity. Thus, the relative velocity between the main stream and the A edge is zero when the wing angle is 90˚. According to Equation (2), the circulation change is static at that time; thus, the supply of vorticity to the lateral vortex shed from the A edge is smaller than that in the case of S = 0.6. Thus, the shear layer is hard to roll up on side A. In contrast to this vortex, the vortex shed from the B edge is stronger than that in the case of S = 0.6 because of the higher relative velocity. The strong vortex forms slightly below the edge. This affects the surface pressure induced by the strong vortex. This makes the prediction of aerodynamic forces difficult, because the induced pressure results from mutual effects involving both the strength of the vortex and the distance from the vortex to the surface.
4. Conclusion
The influence of the shape of plate and the role of vortex dynamics were investigated, herein we propose using a rotating plate about its spanwise axis. We conducted numerous flight tests using a model plane to understand the factors influencing the stability of its flight. The rectangular plate with an aspect ratio of 7 was the suitable for the flight with an auto rotating. The difficulty of rotation was examined with an increasing of moment of inertia. In addition, to understand three-dimensional effects and

Figure 8. Time evolution of the flow field around the rotating wing without end plates in an open water channel. Velocity was measured by PIV. Lines represent stream lines. Color of a vector represents the magnitude of velocity. The passage of time is shown from left to right figures. Time interval of each figure is π/4 phase of a revolution cycle. Symbols A and B at edges of the plate distinguish the edges during the revolution in one cycle. (a) S = 0.6 and (b) S = 1.0.
the unsteadiness of the tip vortex, we observed the formation of vortices near the tip of the rotating plate by a real-time PIV system. The lateral vortex that separates from the forward and backward edges is found to be contaminated by the tip vortex. However, attaching end plates at the tips effectively prevents this contamination, and we demonstrated stable flight of the model plane with end plates attached. Vortices generated from the backward-rotating edge are weaker than those generated from the forward-rotating edge. However, the former move near the wing surface together with the plate; therefore, the induced surface pressure is larger.
REFERENCES
- R. Mittal, V. Seshadri and H. S. Udaykumar, “Flutter, Tumble and Vortex Induced Autorotation,” Theoretical and Computational Fluid Dynamics, Vol. 17, No. 3, 2004, pp. 1-6. doi:10.1007/s00162-003-0101-5
- S. A. Ansari, R. Zbikowski and K. Knowles, “Aerodynamic Modeling of Insect-Like Flapping Flight for Micro Air Vehicles,” Progress in Aerospace Science, Vol. 42, No. 2, 2006, pp. 129-172. doi:10.1016/j.paerosci.2006.07.001
- L. Mahadevan, W. S. Ryu and A. D. T. Samuel, “Tumbling Cards,” Physic of Fluid, Vol. 11, No. 1, 1999, pp. 1-3. doi:10.1063/1.869919
- K. Hirata, M. Hayakawa and J. Funaki, “On Tumbling of a Two-Dimensional Plate under Free Flight,” Journal of Fluid Science and Technology, Vol. 6, No. 2, 2011, pp. 177-191. doi:10.1299/jfst.6.177
- A. Andersen, U. Pesavento and Z. J. Wang, “Analysis of Transitions between Fluttering, Tumbling and Steady Descent of Falling Card,” Journal of Fluid Mechanics, Vol. 542, 2005, pp. 65-90. doi:10.1017/S002211200500594X
- U. Pesavento and Z. J. Wang, “Falling Paper: NavierStokes Solutions, Model of Fluid Forces, and Center of Mass Elevation,” Physical Review Letters, Vol. 93, No.14, 2004, Article ID: 144501. doi:10.1103/PhysRevLett.93.144501
- C. Jin and K. Xu, “Numerical Study of the Unsteady Aerodynamics of Freely Falling Plates,” Communications in Computational Physics, Vol. 3, No. 4, 2008, pp. 834- 851.

