World Journal of Mechanics
Vol.1 No.5(2011), Article ID:8160,14 pages DOI:10.4236/wjm.2011.15028
Modified Differential Transform Method (DTM) Simulation of Hydromagnetic Multi-Physical Flow Phenomena from a Rotating Disk
1Mechanical Engineering Department, Engineering Faculty of Bu-Ali Sina University, Hamedan, Iran
2Energy and Biomechanics Research, Aerospace Engineering, Department of Engineering and Mathematics, Sheaf Building, Sheffield Hallam University, Sheffield, UK
3Department of Mathematics, Narajole Raj College, West Bengal, India
E-mail: O.Beg@shu.ac.uk, g_swapan2002@yahoo.com
Received July 21, 2011; revised August 20, 2011; accepted September 14, 2011
Keywords: Differential transform method, Padé approximants, Thermal-diffusion, Heat transfer, Soret effect, Boundary-layers, Hydromagnetics, Slip, Dissipation, Electromagnetic processing of materials
ABSTRACT
A similarity solution for the steady hydromagnetic convective heat and mass transfer with slip flow from a spinning disk with viscous dissipation and Ohmic heating yields a system of non-linear, coupled, ordinary differential equations. These equations are analytically solved by applying a newly developed method namely the DTM-Padé technique which is a combination of the Differential Transform Method (DTM) and the Padé approximation. A full analytical solution is presented, as a benchmark for alternative numerical solutions. DTM-Padé is implemented without requiring linearization, discretization, or perturbation, and holds significant potential for solving strongly nonlinear differential equations which arise frequently in fluid dynamics. The regime studied is shown to be controlled by the slip parameter (g), magnetohydrodynamic body force parameter (M), Eckert (viscous heating) number (Ec), Schmidt number (Sc), Soret number (Sr), Dufour number (Du) and Prandtl number (Pr). The influence of selected parameters on the evolution of dimensionless velocity, temperature and concentration distributions is studied graphically. Increasing magnetic field (M) is found to significantly inhibit the radial (f) and tangential (g) velocities, but to accentuate the axial velocity field (h); furthermore temperature (q) and concentration (f) are both enhanced with increasing M. Increasing Soret number (Sr) acts to boost the dimensionless concentration (f). Temperatures are significantly elevated in the boundary layer regime with a rise in Eckert number (Ec). Excellent correlation between the DTM-Padé technique and numerical (shooting) solutions is achieved. The model has important applications in industrial energy systems, process mechanical engineering, electromagnetic materials processing and electro-conductive chemical transport processes.
1. Introduction
Hydromagnetic flow with heat and mass transfer from a rotating disk is a fundamental regime of interest in diverse branches engineering including magnetic materials processing [1], industrial energy conversion [2], magnetohydrodynamic tribological systems [3,4], rotating disk voltammetry in chemical synthesis [5] etc. Static magnetic fields are frequently implemented in solidification processing for metallic alloys wherein they can be employed strategically to regulate melt flow and solidify structures in the continuous casting of steels [6]. Electromagnetic processing can significantly improve the quality of products in numerous mechanical and chemical engineering technologies. In magnetohydrodynamic disk generators, high power density can be produced with low environmental issues, and such systems are increaseingly being employed in modern thermal power systems and incorporated into enhancing industrial energy management [7,8]. Such applications have stimulated considerable interest in the mechanical engineering research community in theoretically and numerically simulating rotating disk hydromagnetic flows in the presence of various supplementary phenomena including, magnetic induction, slip, viscous heating, thermal radiation etc. Intani et al. [9] used the finite element method to study the velocity and induced magnetic fields in a rotating hydromagnetic disk generator. Aboul-Hassan and Attia [10] investigated the effects of Hall currents on hydromagnetic rotating disk flow in the presence of an axial static uniform magnetic field using a shooting method. Turkyilmazoglu [11] studied the transient hydromagnetic convection flow from a porous spinning disk in the presence of uniform normal magnetic field, using a compact, unconditionally stable, implicit spectral numerical integration algorithm.
The above studies did not consider thermo-diffusion or diffuso-thermal effects. Thermodiffusion, also called thermal diffusion or the Soret effect corresponds to species differentiation developing in an initial homogeneous mixture subjected to a thermal gradient. On the other hand, the Soret effect has been also utilized for isotope separation and in mixture between gases with very light molecular weight, such as 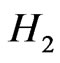 or
or  and of medium molecular weight, such as
and of medium molecular weight, such as 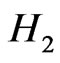 or air. In many studies the Dufour and Soret effects are neglected, on the basis that they are of a smaller order of magnitude than the effects described by Fourier’s (thermal conduction) and Fick’s (species diffusion) laws. However, in certain industrial processing operations, such phenomena may arise and infact exert an important role. Postelnicu [12] studied numerically the influence of a magnetic field on heat and mass transfer by natural convection from vertical surfaces in porous media considering Soret and Dufour effects. Bhargava et al. [13] used the finite element method to analyze the oscillatory reactive double-diffusive magnetohydrodynamic boundary layer flow with Soret and Dufour effects. Bég et al. [14] used shooting quadrature to simulate the influence of Soret and Dufour effects on natural convection hydromagnetic flow from a stretching sheet in porous media. Maleque and Sattar [15] have also studied MHD natural convection flow with mass transfer incorporating the influence of thermaldiffusion effects.
or air. In many studies the Dufour and Soret effects are neglected, on the basis that they are of a smaller order of magnitude than the effects described by Fourier’s (thermal conduction) and Fick’s (species diffusion) laws. However, in certain industrial processing operations, such phenomena may arise and infact exert an important role. Postelnicu [12] studied numerically the influence of a magnetic field on heat and mass transfer by natural convection from vertical surfaces in porous media considering Soret and Dufour effects. Bhargava et al. [13] used the finite element method to analyze the oscillatory reactive double-diffusive magnetohydrodynamic boundary layer flow with Soret and Dufour effects. Bég et al. [14] used shooting quadrature to simulate the influence of Soret and Dufour effects on natural convection hydromagnetic flow from a stretching sheet in porous media. Maleque and Sattar [15] have also studied MHD natural convection flow with mass transfer incorporating the influence of thermaldiffusion effects.
Dissipation effects may also contribute significantly to flow and heat/mass transfer characteristics in magnetohydrodynamic transport phenomena. These may be simulated as viscous dissipation and Joule heating (Ohmic dissipation). Attia [16] considered transpiration and Ohmic heating effects on rotating disk hydromagnetic flow with ionslip. Zueco et al. [17] used network simulation methodology to simulate the combined effects of viscous and Joule heating, thermophoresis and thermal conductivity variation on hydromagnetic convection boundary layers. Bég et al. [18] have studied viscous and Joule heating effects on transient magnetohydrodynamic plasma flow in a porous medium channel, using network simulation. Osalusi et al. [19] have employed shooting quadrature to analyze the combined Soret, Dufour, viscous and Ohmic heating effects on hydromagnetic slip flow from a spinning disk. Sibanda and Makinde [20] used a Newton-Raphson shooting method along with fourth-order Runge-Kutta integration algorithm to study the steady hydromagnetic convection from a spinning disk embedded in a porous medium with viscous and Ohmic dissipation, and additionally Hall currents. They showed that magnetic field inhibits the flow due to the opposing Lorentz force generated by the magnetic field and that both magnetic field and the Eckert number (dissipation parameter) enhance the heat transfer efficiency.
In the present study we consider a similar regime to that studied by Osalusi et al. [19], using a novel technique, the DTM-Padé method [21], which can be applied directly to nonlinear differential equations without requiring linearization, discretization and therefore, is not affected by errors associated with discretization. This technique therefore provides mechanical engineering researchers with a very robust benchmark for verifying purely numerical solutions. In this article we obtain approximate analytic solutions by the combination of the DTM and the Padé approximants for rotating hydromagnetic flow, heat and mass transfer from a spinning disk with Soret, Dufour, viscous and Joule heating effects.
Therefore, this paper has been organized as follows. In Section 2, the mathematical flow model is developed. In Sections 3 and 4 we elaborate the fundamentals of the DTM approach and the theory of Padé approximants, respectively. In Section 5, we extend the application of the DTM-Padé to construct the approximate solutions for the transformed, nonlinear, coupled, ordinary differential equations governing the rotating magnetohydrodynamic flow regime. In Section 6 the graphical results are presented with a detailed discussion. Conclusions are summarized in Section 7.
2. Mathematical Model
We consider the steady, hydromagnetic, incompressible Von Karman convective and slip flow due to a rotating disk in the presence of viscous dissipation and Ohmic heating with effects of thermo-diffusion (Soret effect) and diffusion-thermo (Dufour effect) effects on combined heat and mass transfer [19]. Figure 1 shows the physical model with coordinate system.
The disk rotates with constant angular velocity  and is placed at
and is placed at  where
where 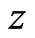 is the vertical axis in the cylindrical coordinates system with
is the vertical axis in the cylindrical coordinates system with  and
and  as the radial and tangential axes, respectively. The components of the flow velocity are
as the radial and tangential axes, respectively. The components of the flow velocity are 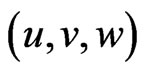 in the directions of increasing
in the directions of increasing 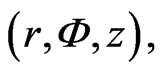 respectively, the pressure is
respectively, the pressure is  and the density of the fluid is
and the density of the fluid is 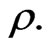
 and
and  are the fluid temperature and concentration, respectively, and the surface of the rotating disk is maintained at a uniform temperature
are the fluid temperature and concentration, respectively, and the surface of the rotating disk is maintained at a uniform temperature 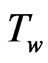 and uniform concentration
and uniform concentration  Far away from the surface, the free stream is sustained at a constant temperature
Far away from the surface, the free stream is sustained at a constant temperature  constant concentration
constant concentration  and at constant pressure
and at constant pressure  The fluid is assumed to be Newtonian, viscous and electricallyconducting. The external uniform magnetic field is applied perpendicular to the surface of the disk i.e. axially, and has a constant magnetic flux density
The fluid is assumed to be Newtonian, viscous and electricallyconducting. The external uniform magnetic field is applied perpendicular to the surface of the disk i.e. axially, and has a constant magnetic flux density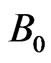 . Since small magnetic Reynolds number is assumed, magnetic induction effects are neglected. In addition, no electric field is assumed to exist and the Hall effect is negligible. The equations governing the motion of the hydromagnetic laminar flow of the homogeneous fluid take the following form
. Since small magnetic Reynolds number is assumed, magnetic induction effects are neglected. In addition, no electric field is assumed to exist and the Hall effect is negligible. The equations governing the motion of the hydromagnetic laminar flow of the homogeneous fluid take the following form
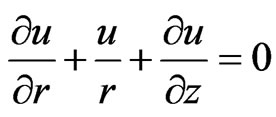 (1)
(1)
 (2)
(2)
 (3)
(3)
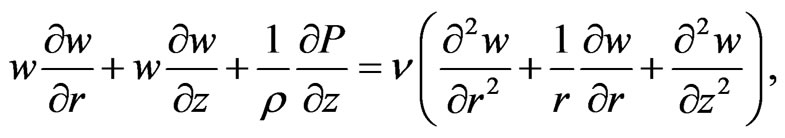 (4)
(4)
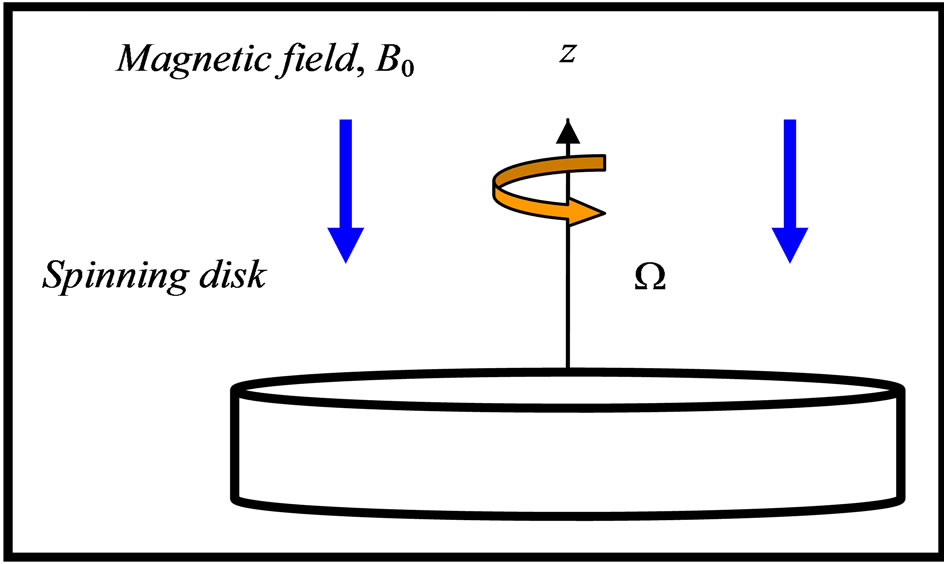
Figure 1. physical model with coordinate system.
 (5)
(5)
 (6)
(6)
where 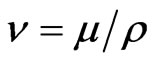 is the kinematic viscosity of the ambient fluid,
is the kinematic viscosity of the ambient fluid, 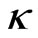 is the thermal conductivity of heat,
is the thermal conductivity of heat, 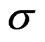 is the electrical conductivity,
is the electrical conductivity, 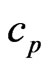 is the specific heat at constant pressure,
is the specific heat at constant pressure, 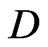 is the molecular diffusion coefficient,
is the molecular diffusion coefficient, 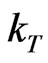 is the thermal-diffusion ratio,
is the thermal-diffusion ratio, 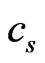 is the concentration susceptibility and
is the concentration susceptibility and  is the mean fluid temperature. The last term on the right-hand side of the energy equation (5) and diffusion equation (6) signifies the Dufour or diffusion-thermo effect and the Soret or thermodiffusion effect, respectively. The boundary conditions are introduced as follows [19]:
is the mean fluid temperature. The last term on the right-hand side of the energy equation (5) and diffusion equation (6) signifies the Dufour or diffusion-thermo effect and the Soret or thermodiffusion effect, respectively. The boundary conditions are introduced as follows [19]:
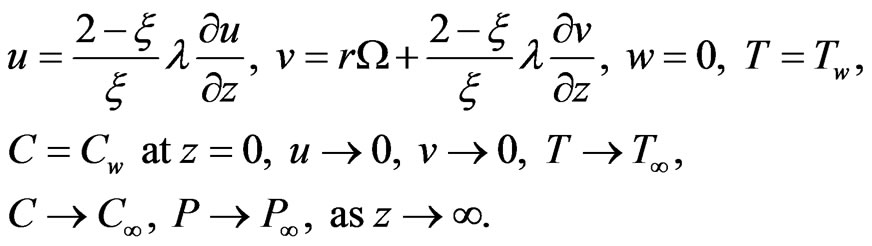 (7)
(7)
The transformed “similarity” nonlinear ordinary differential equations (9)-(13) are obtained by initially performing a non-dimensionalization [19] and subsequently by introducing a dimensionless normal distance from the disk, 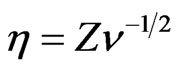 along with the von Karman transformations:
along with the von Karman transformations:
 (8)
(8)
Where 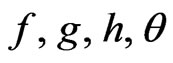 and
and 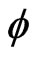 are non-dimensional functions of modified dimensionless vertical (axial) coordinate
are non-dimensional functions of modified dimensionless vertical (axial) coordinate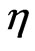 .
.
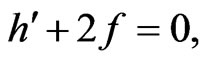 (9)
(9)
 (10)
(10)
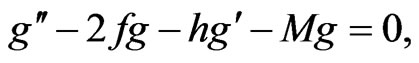 (11)
(11)
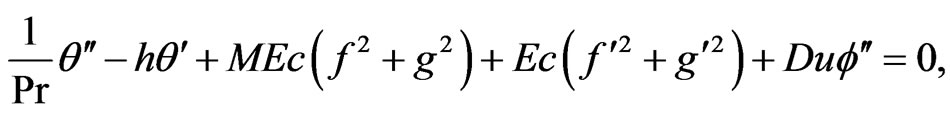 (12)
(12)
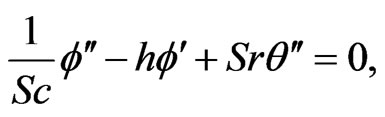 (13)
(13)
where  is the magnetic (hydromagnetic body force) parameter,
is the magnetic (hydromagnetic body force) parameter,  is the ordinary Prandtl number,
is the ordinary Prandtl number,  is the Eckert number,
is the Eckert number,  is the Du-four number,
is the Du-four number,  is the Schmidt number,
is the Schmidt number,  is the Soret number and the prime symbol denotes a derivative with respect to
is the Soret number and the prime symbol denotes a derivative with respect to 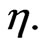 The transformed boundary conditions are given as:
The transformed boundary conditions are given as:
 (14)
(14)
 (15)
(15)
 (16)
(16)
where 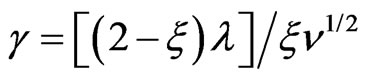 is the slip factor, The boundary conditions (14)-(16) imply that both the radial and tangential velocity components as well as temperature and concentration vanish sufficiently far away from the rotating disk, whereas the axial velocity component is anticipated to approach a (yet unknown) asymptotic limit for sufficiently large
is the slip factor, The boundary conditions (14)-(16) imply that both the radial and tangential velocity components as well as temperature and concentration vanish sufficiently far away from the rotating disk, whereas the axial velocity component is anticipated to approach a (yet unknown) asymptotic limit for sufficiently large  -values.
-values.
3. Differential Transform Method (DTM)
The concept of DTM was first introduced by Zhou [22] and employed to solve both linear and nonlinear initial value problems in electric circuit theory. In this method, we applied certain transformation rules. The governing differential equations and the boundary conditions of the system are transformed into a set of algebraic equations and the solution of these algebraic equations yields the desired solution of the problem. Also, DTM does not require “perturbation” parameters. The validity of DTM is independent of whether or not there exist small parameters in the considered equation. Therefore, as with other semi-analytical techniques such as the Homotopy Analysis Method [23,24] (HAM) and the Homotopy Perturbation Method (HPM) [25,26], DTM can overcome the foregoing restrictions and limitations of perturbation methods. Rashidi and Erfani [27] used DTM to solve Burgers’ and nonlinear heat transfer equations demonstrating very good correlation with HAM solutions. In recent years, DTM has been successfully employed to solve many types of nonlinear problems arising in diverse branches of applied physics and engineering sciences. These include stability problems in structural dynamics [28], Lane-Emden type differential equations in astrophysical fluid dynamics and thermionic current systems [29], rotating hydromagnetic flow stability [30], water wave hydrodynamics [31], the sine-Gordon equation which arise in differential geometry and studies of propagation of magnetic flux [32], soil-structure interaction problems in earthquake engineering [33], the regularized long wave (RLW) equation in plasma wave hydromagnetics [34], boundary layer theory in aerodynamics [35], elasto-dynamics [36] and unsteady, nonlinear thermal conduction modelling in mechanical engineering components [37]. All these successful applications have extensively verified the validity, effectiveness, and flexibility of DTM.
DTM constructs for differential equations an analytical solution in the form of a power series. Furthermore, power series are not useful for large values of , say
, say 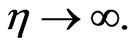 It is now well-known that the Padé approximants [38,39] have the advantage of manipulating the polynomial approximation into rational functions of polynomials. It is therefore essential to combination of the series solution, obtained by the DTM with the Padé approximant to provide an effective tool to handle boundary value problems at infinite domains. One of the first successful applications of DTM to boundary-layer flows was presented by Rashidi and Domairry [40] and Rashid [41]. Rashidi and Erfani [42] also demonstrated the applicability of the DTM approach for convection boundary layer flows over a flat plate with convective surface boundary conditions. The DTM approach has thusfar not received significant attention in rotating hydromagnetic fluid dynamics, and this is one of the objectives of the present paper. Prior to developing a DTM solution to the nonlinear rotating disk flow regime under consideration, we provide a summary of the fundamental concepts of DTM, as an aid to readers.
It is now well-known that the Padé approximants [38,39] have the advantage of manipulating the polynomial approximation into rational functions of polynomials. It is therefore essential to combination of the series solution, obtained by the DTM with the Padé approximant to provide an effective tool to handle boundary value problems at infinite domains. One of the first successful applications of DTM to boundary-layer flows was presented by Rashidi and Domairry [40] and Rashid [41]. Rashidi and Erfani [42] also demonstrated the applicability of the DTM approach for convection boundary layer flows over a flat plate with convective surface boundary conditions. The DTM approach has thusfar not received significant attention in rotating hydromagnetic fluid dynamics, and this is one of the objectives of the present paper. Prior to developing a DTM solution to the nonlinear rotating disk flow regime under consideration, we provide a summary of the fundamental concepts of DTM, as an aid to readers.
Consider a function 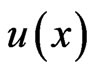 which is analytic in a domain
which is analytic in a domain  and let
and let 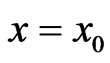 represent any point in the
represent any point in the 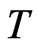 The function
The function 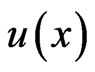 is then represented by a power series whose centre is located at
is then represented by a power series whose centre is located at  The differential transform of the function
The differential transform of the function 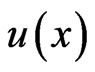 is given by:
is given by:
 (17)
(17)
where 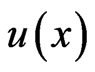 is the original function and
is the original function and 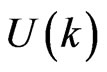 the transformed function. The inverse transformation is defined as follows
the transformed function. The inverse transformation is defined as follows
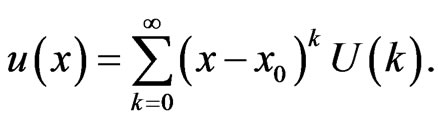 (18)
(18)
Combining Equations (17) and (18), we arrive at:
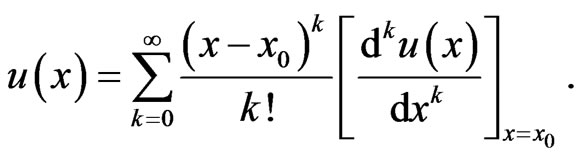 (19)
(19)
Considering Equation (19), it is apparent that the concept of the DTM is derived from Taylor series expansion. However, DTM does not evaluate the derivatives symbolically. In practical applications, the function  is expressed by a finite series and Equation (18) can be rewritten as follows
is expressed by a finite series and Equation (18) can be rewritten as follows
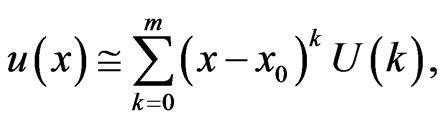 (20)
(20)
which implies that 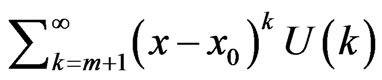 is negligibly small. Usually, the value of
is negligibly small. Usually, the value of 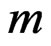 is decided by convergence of the series coefficients. We have documented operations for differential transformed functions about the point
is decided by convergence of the series coefficients. We have documented operations for differential transformed functions about the point  in Table 1 (see Appendix 1) and we assume that
in Table 1 (see Appendix 1) and we assume that 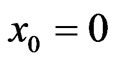 in the following sections.
in the following sections.
4. The Padé Approximants
Suppose that we are given a power series  representing a function
representing a function  so that
so that
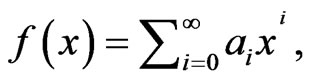 (21)
(21)
a Padé approximant is a rational fraction and the notation for such a Padé approximant is [38,39]:
 (22)
(22)
where 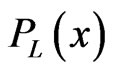 is a polynomial of degree at most
is a polynomial of degree at most 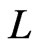 and
and  is a polynomial of degree at most
is a polynomial of degree at most 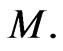 we have
we have
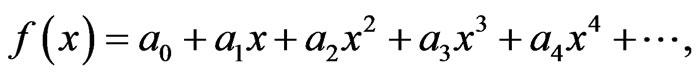 (23)
(23)
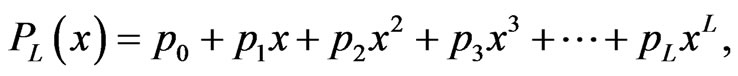 (24)
(24)
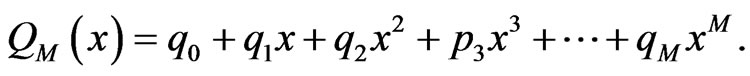 (25)
(25)
Inspection of Equation (22) reveals that there are  numerator coefficients and
numerator coefficients and 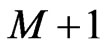 denominator coefficients. Since we can clearly multiply the numerator and denominator by a constant and leave
denominator coefficients. Since we can clearly multiply the numerator and denominator by a constant and leave  unchanged, we impose the normalization condition:
unchanged, we impose the normalization condition:
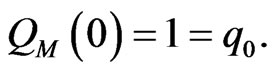 (26)
(26)
Therefore, there are  independent numerator coefficients and
independent numerator coefficients and 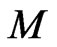 independent denominator coefficients, making
independent denominator coefficients, making  unknown coefficients in all. This number suggests that normally the
unknown coefficients in all. This number suggests that normally the 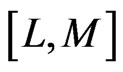 ought to fit the power series Equation (21) through the orders
ought to fit the power series Equation (21) through the orders 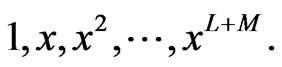 Using the recommendation provided in [38,39], we know that the
Using the recommendation provided in [38,39], we know that the  approximant is uniquely determined. In the notation of formal power series:
approximant is uniquely determined. In the notation of formal power series:
 (27)
(27)
By cross-multiplying Equation (27), we find that:
 (28)
(28)
These yield the following set of equations:
 (29)
(29)
and
 (30)
(30)
where 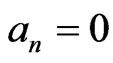 for
for 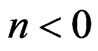 and
and  for
for  If Equations (29) and (30) are non-singular, then a direct solution is tangible:
If Equations (29) and (30) are non-singular, then a direct solution is tangible:
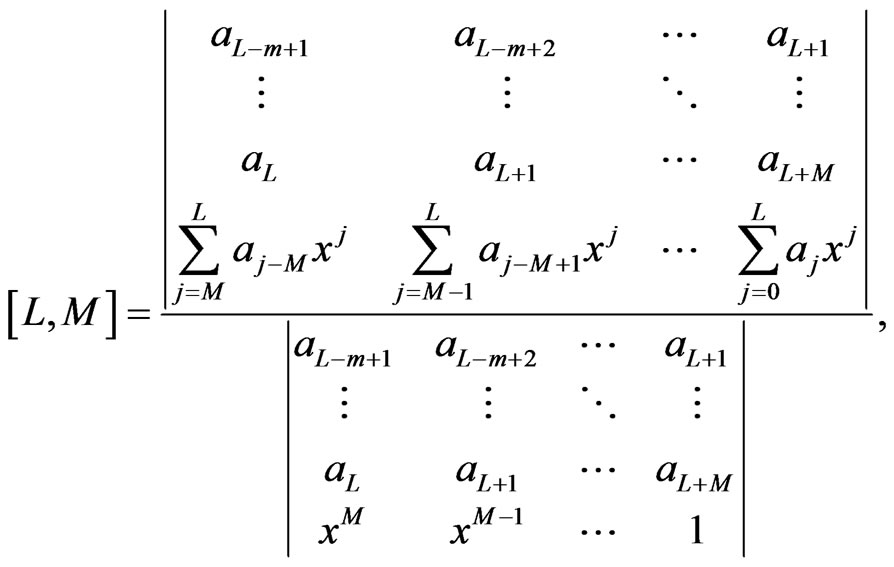 (31)
(31)
If the lower index on a sum exceeds the upper, the sum is replaced by zero. Alternate forms are:
 (32)
(32)
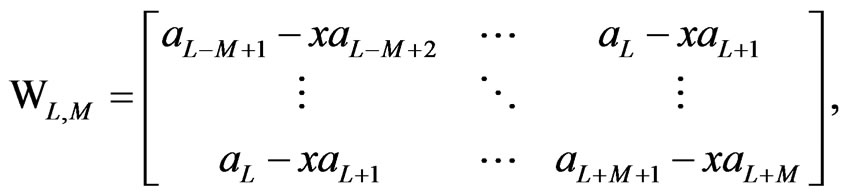 (33)
(33)
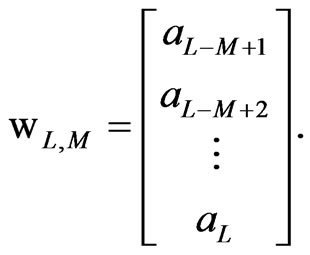 (34)
(34)
The construction of 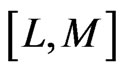 approximants involves only algebraic operations [38,39]. Each choice of
approximants involves only algebraic operations [38,39]. Each choice of  degree of the numerator and
degree of the numerator and 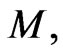 degree of the denominator, leads to an approximant. The major difficulty in applying this technique is how to direct the choice in order to obtain the best approximant. This requires a criterion which dictates the choice of approximation, depending on the shape of the solution. A criterion which has worked well here is the choice of
degree of the denominator, leads to an approximant. The major difficulty in applying this technique is how to direct the choice in order to obtain the best approximant. This requires a criterion which dictates the choice of approximation, depending on the shape of the solution. A criterion which has worked well here is the choice of 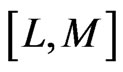 approximants such that
approximants such that  Using the symbolic computation software MATHEMATICA, we directly employ the command “Padé Approximant” about the point
Using the symbolic computation software MATHEMATICA, we directly employ the command “Padé Approximant” about the point 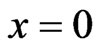 to generate the Padé approximant of
to generate the Padé approximant of  in the following sections.
in the following sections.
5. Analysis with DTM-Padé Simulation
Taking the one-dimensional differential transform, from Table 1 to Equations (9)-(13), the following transformations are obtained:
 (35)
(35)
 (36)
(36)
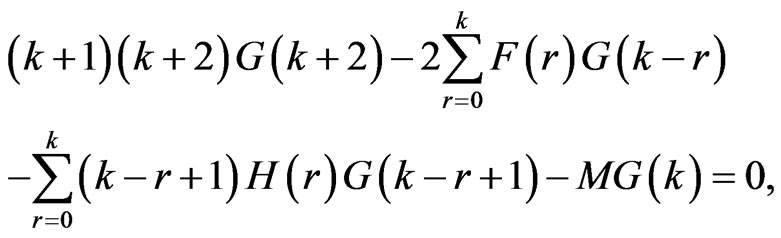 (37)
(37)
 (38)
(38)
 (39)
(39)
where 


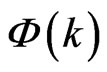 and
and  are the transformed functions of
are the transformed functions of 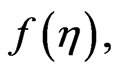


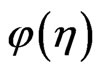 and
and 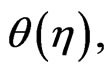 respectively and are given by:
respectively and are given by:
 (40)
(40)
 (41)
(41)
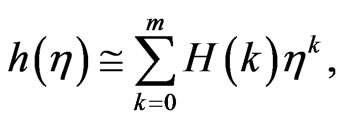 (42)
(42)
 (43)
(43)
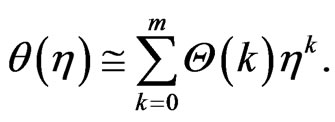 (44)
(44)
The differential transform of the boundary conditions Equations (14)-(16) are as follows:
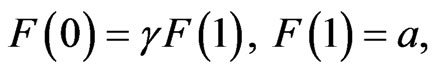 (45)
(45)
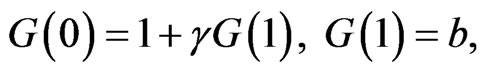 (46)
(46)
 (47)
(47)
 (48)
(48)
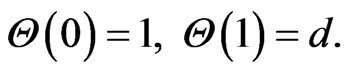 (49)
(49)
Substituting Equations (45)-(49) into Equations (35)- (39) and employing the recursive method we can calculate other values of 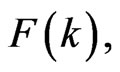


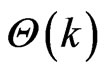 and
and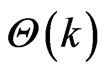 . Hence, substituting all
. Hence, substituting all 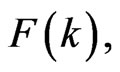
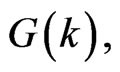

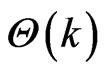 and
and 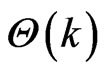 into Equations (40)-(44), we have series solutions as given below:
into Equations (40)-(44), we have series solutions as given below:
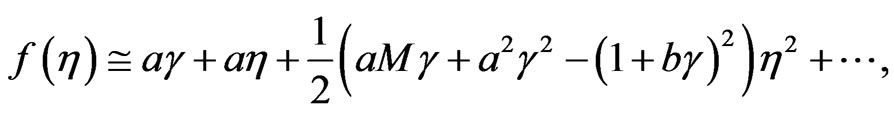 (50)
(50)
 (51)
(51)
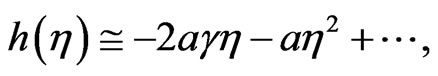 (52)
(52)
 (53)
(53)
 (54)
(54)
The best procedure for enlarging the convergence domain of the truncated series solution is to employ the Padé approximant where the polynomial approximation is converted into a ratio of two polynomials. Without using the Padé approximant, the analytical solution as obtained by DTM, cannot satisfy the boundary conditions at infinity. It is therefore essential to combine the series solution obtained by the DTM, with the Padé approximant, to provide an effective tool for handling boundary value problems in infinite domains. Hence, applying the Padé approximation to Equations (50)-(54) and using the asymptotic boundary conditions in Equation (16) at 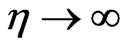 we can obtain
we can obtain 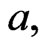
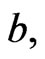
 and
and 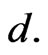 The number of terms required is determined by the convergence of the numerical values to the desired accuracy, since a higher order approximation produces greater accuracy.
The number of terms required is determined by the convergence of the numerical values to the desired accuracy, since a higher order approximation produces greater accuracy.
6. Results and Discussion
The flow regime is controlled by a number of thermophysical parameters: magnetohydrodynamic body force parameter (M), Soret number (Sr), Dufour number (Du), Eckert number (Ec), Prandtl number (Pr) and Schmidt number (Sc) and slip parameter (g). The first six of these parameters arise in the boundary layer equations (9) to (13); the last parameter (g) arises in the boundary conditions (14). This parameter is linked to the slip of particles on the disk surface. This arises when the mean free path (l) of fluid particles is of the same order as the characteristic dimension of the flow domain; the classical “noslip” wall boundary condition is then inadequate and a Knudsen number is invoked to simulate slip effects [44]; a slip factor is effectively employed to simulate the wall slip. Further details of slip effects are provided in [45]. In the present simulations, we adopt a Prandtl number (Pr) corresponding to air at 20 Celsius i.e. Pr = 0.71. At this Prandtl number, the diluting chemical species generally encountered in mechanical engineering operations posses a Schmidt number (Sc) in the range from 0.1 to 10. Sc = 0.22 corresponds to Hydrogen; Sc = 0.6 corresponds to water vapor (which represents a diffusing chemical species of most common interest in air) and Sc = 0.75 is an accurate representation of oxygen diffusing in air. We further note that larger values of Sc correspond to higher molecular weight gases appropriate values for Sc are, for methanol diffusing in air, Sc = 1.0, and for ethylbenzene in air (Sc = 2.0), as indicated by Gebhart and Pera [43]. Sc measures the relative effectiveness of momentum and mass transport by diffusion. In all our computations, Sc ¹ Pr, which physically implies that the thermal and species diffusion regions are of different extents, and therefore thermal and species boundary layer thicknesses will also be different. To verify the accuracy of the present DTMPadé computations, we have compared the DTM-Padé results with the results generated with a numerical shooting method, coupled with a Runge-Kutta integration scheme. Figures 2 and 3 show the radial velocity 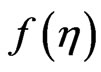 distributions obtained by the DTM-Padé approach utilizing the diagonal Padé approximation [10] in comparison with the numerical solutions. Figure 2 show the radial velocity for the case of slip factor
distributions obtained by the DTM-Padé approach utilizing the diagonal Padé approximation [10] in comparison with the numerical solutions. Figure 2 show the radial velocity for the case of slip factor
 and Figure 3 depicts the radial velocity for the case of magnetic interaction parameter,
and Figure 3 depicts the radial velocity for the case of magnetic interaction parameter, . Excellent agreement is demonstrated in both figures 2 and 3 between DTM-Padé and the numerical results. For analytical solution, the convergence analysis was performed and in Equations (40)- (44), the value of
. Excellent agreement is demonstrated in both figures 2 and 3 between DTM-Padé and the numerical results. For analytical solution, the convergence analysis was performed and in Equations (40)- (44), the value of 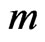 is selected equal to 20. The order of Padé approximation [L, M] [10] has sufficient accuracy; we further highlight that if the order of Padé approximation is increased, the accuracy of the solution increases. Figure 2 also shows that an enhancement in
is selected equal to 20. The order of Padé approximation [L, M] [10] has sufficient accuracy; we further highlight that if the order of Padé approximation is increased, the accuracy of the solution increases. Figure 2 also shows that an enhancement in
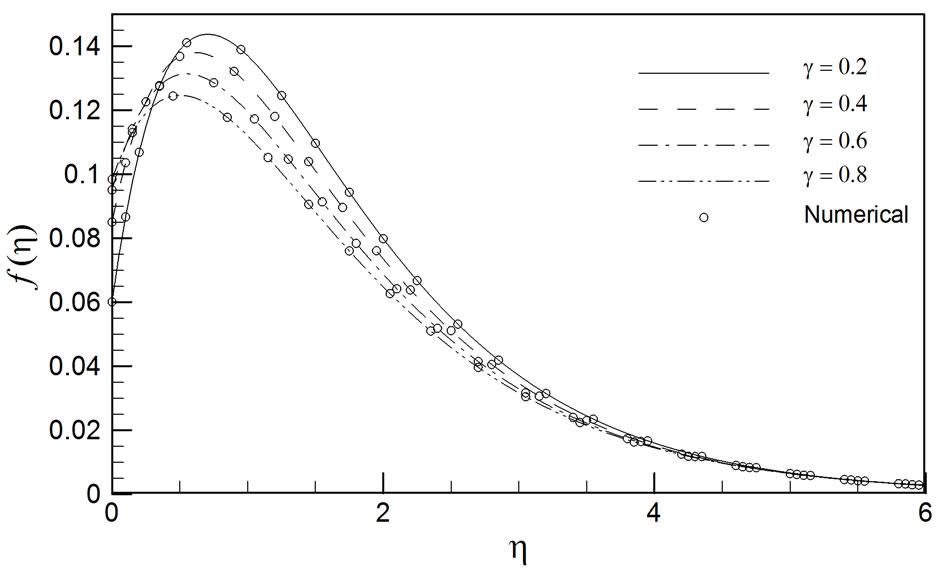
Figure 2. Analytical solutions for radial velocity, f(η) variation obtained by the DTM-Padé scheme in comparison with the numerical solutions (M = 0.2, Ec = 0.2, Du = 0.06, Sc = 0.2, Sr = 1, Pr = 0.71).
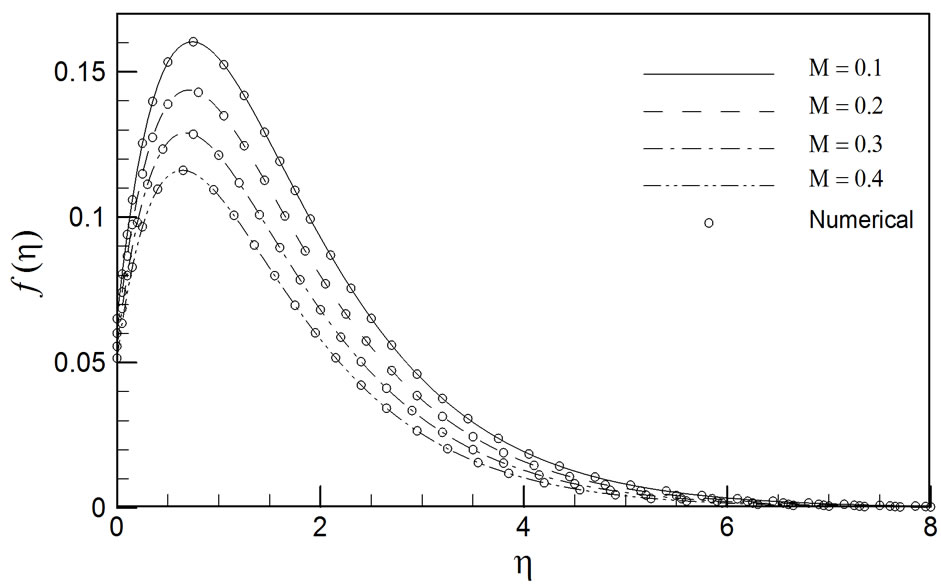
Figure 3. Analytical solutions for radial velocity, f(η) variation obtained by the DTM-Padé scheme in comparison with the numerical solutions (γ = 0.2, Ec = 0.2, Du = 0.06, Sc = 0.2, Sr = 1, Pr = 0.71).
wall slip factor serves to elevate the radial flow i.e. increase f(h) values close to the disk surface, but conversely decrease them further from the wall. The rotating disk regime acts much like a fan system drawing fluid axially inward from the surrounding medium towards the disk surface. Since no transpiration occurs at the disk surface i.e. it is solid (suction = injection = 0), therefore the incoming fluid is turned and discharges in the radial direction along the disk. The centrifugal force associated with the spinning disk motion causes the outward radial flow. Radial flow therefore grows from the disk surface as we proceed in an axial direction, peaking and then descending to zero far from the disk surface in the free stream. Increasing slip coefficient will serve to enhance the radial flow at the disk surface (h = 0) since g i.e. the slip parameter effect will be maximized here; further from the disk surface as we progress into the boundary layer regime, transverse to the disk the wall slip effect will be gradually diminished. An increase in magnetic parameter (M) also acts to strongly retard the radial flow development. In the transformed radial momentum equation (10), the magnetic field term arises in the Lorentizian hydromagnetic drag force, -Mf’; this linear body force term is clearly accentuated with an increase in M and therefore greater magnetic field will serve to inhibit the radial flow. This is of great benefit in magnetic materials processing operations, utilizing static transverse uniform magnetic field, since it allows a strong regulation of the flow field in the vicinity of the disk. Very similar results have also been computed by Osalusi et al. [19] who used shooting quadrature and more recently by Bég et al. [45], who employed Network Simulation Methodology (NSM) and neglected Soret and Dufour effects.
Figure 4 illustrates the effect of the Soret number (Sr) on the evolution of species (concentration) in the boundary layer regime. Sr signifies the effect of temperature gradients inducing substantial mass (species) diffusion effects. With a rise in Sr, there is a significant elevation in j values. A smooth decay in profiles is evident, from the disk surface to the free stream. Similar trends have been reported by Postelnicu [12], Bhargava et al. [13], Bég et al. [14] and Maleque and Sattar [15]. Osalusi et al. [19] also achieved similar results and we emphasize here that significant modifications in the concentration profiles are generally obtained when Du (i.e. Dufour number, which simulates the effects of concentration gradients on thermal energy flux in the regime), is non-zero. In the present case we have used Du = 0.06.
The effects of Schmidt number (Sc) on the temperature and concentration distributions in the regime are shown in figures 5 and 6, respectively. With increasing Sc there is a slight elevation in temperature (q) magnitudes; concentration (j) magnitudes are however very
Figure 4. Influence of Sr (Soret number) on the concentration (species) profiles (γ = 0.2, M = 0.2, Du = 0.06, Ec = 0.2, Sr = 1, Pr = 0.71).
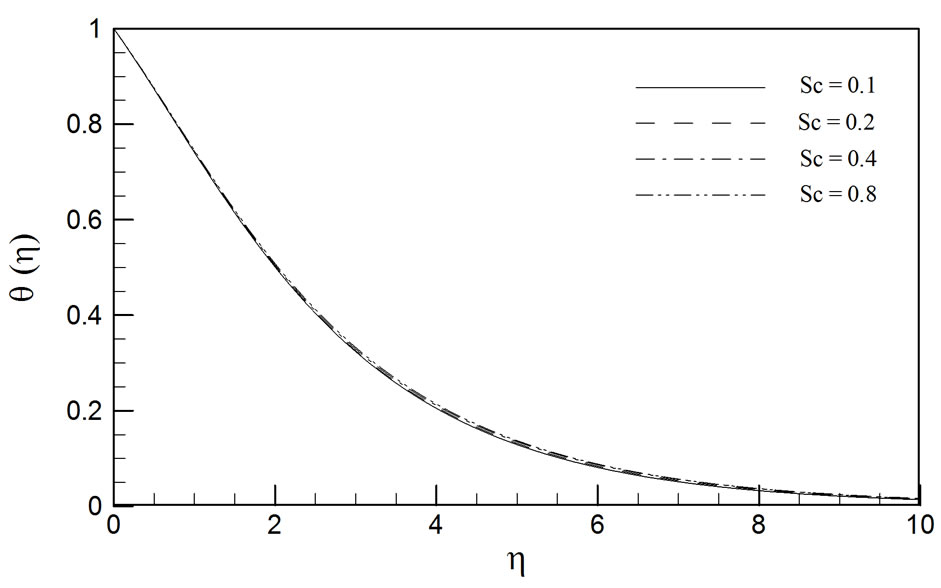
Figure 5. Influence of Sc (Schmidt number) on the temperature profiles (γ = 0.2, M = 0.2, Du = 0.06, Ec = 0.2, Sr = 1, Pr = 0.71).
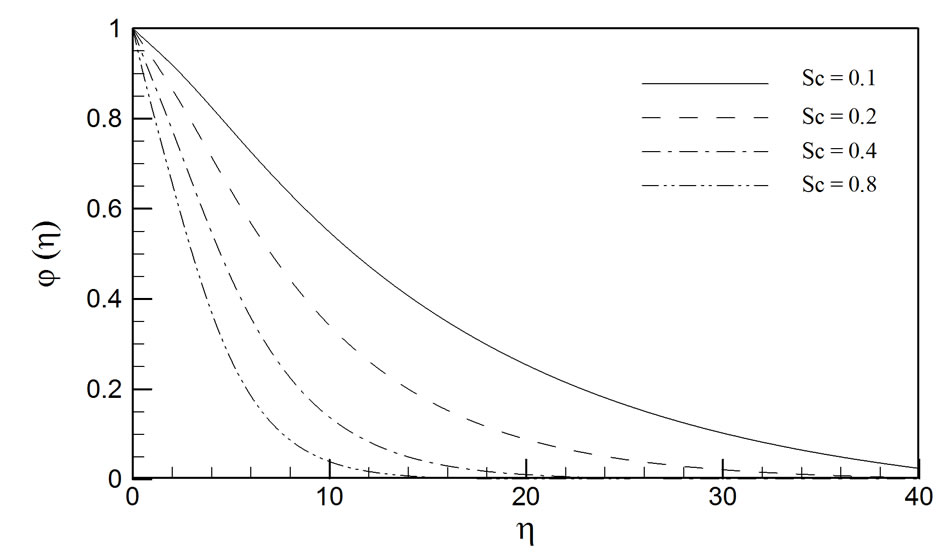
Figure 6. Influence of Sc (Schmidt number) on the concentration (species) profiles (γ = 0.2, M = 0.2, Du = 0.06, Ec = 0.2, Sr = 1, Pr = 0.71).
strongly decreased with increasing Sc. Schmidt number embodies the relative rate of momentum diffusion to species (mass) diffusion. For Sc = 1, both momentum and species diffuse at the same rate and the momentum and species (concentration) boundary layers on the rotating disk are of the same order of thickness. For Sc < 1, as considered in our DTM-Padé computations, species diffusivity will exceed the momentum diffusivity in the regime. As such concentrations will be progressively diminished through the boundary layer. In all cases, as shown in figure 6, the profiles follow a smooth decay from the disk surface to the edge of the boundary layer, indicating that the DTM-Padé computations have converged smoothly.
Figures 7 and 8 depict the response of the temperature (q) and concentration (j) functions, to various Eckert numbers (Ec). Ec represents the ratio of the kinetic energy of the flow to the boundary layer enthalpy difference as described by Schlichting [46]. Ec features in two terms in the transformed energy equation (12), viz the Joule heating (Ohmic magnetic dissipation) term, MEc (f’2 + g2), and the conventional viscous heating term Ec (f’2 + g2). Although Ec is used in high altitude rocket aero-thermodynamics (where the prescribed temperature difference is of the same order of magnitude as the absolute temperature in the free stream), in the context of low speed incompressible flows, as studied here, Ec signifies the difference between the total mechanical power input and the smaller amount of total power input which produces thermodynamically reversible effects, i.e. eleva-

Figure 7. Influence of Ec (Eckert number) on the temperature profiles (γ = 0.2, M = 0.2, Du = 0.06, Sc = 0.2, Sr = 1, Pr = 0.71).
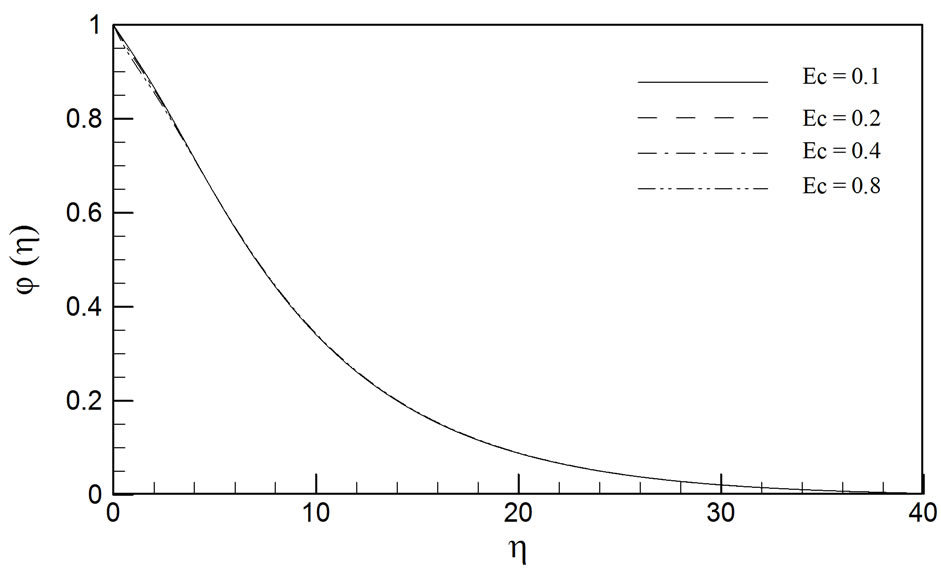
Figure 8. Influence of Ec (Eckert number) on the concentration profiles (γ = 0.2, M = 0.2, Du = 0.06, Sc = 0.2, Sr = 1, Pr = 0.71).
tions in kinetic and potential energy. This difference constitutes the energy dissipated as thermal energy by viscous effects, i.e. work done by the viscous fluid in overcoming internal friction, hence the term viscous heating. Positive values of Ec correspond to disk cooling, i.e. loss of heat from the disk surface to the fluid; negative values imply the reverse, i.e. disk heating wherein heat is received by the disk from the fluid. In this study we restrict attention to Ec > 0. A significant increase in temperature in the boundary layer is observed (figure 7) with an increase in Ec from 0.1 through 0.2, 0.4 to 0.8. As expected there is negligible alteration in the concentration profiles (figure 8) with a change in Ec.
Figures 9-13 illustrate the distributions of radial velocity (f), tangential velocity (g), axial velocity (h), temperature (q) and concentration (j) profiles with various slip parameters, . In all these plots, there is a weak magnetic field acting transverse to the disk (M = 0.2). Increasing g serves to elevate the radial velocity (at or near the disk surface), but strongly decelerates the tangential flow, both at the disk surface and through the boundary layer regime. The shear-driven flow (figure 10) in the tangential (azimuthal) direction, g, is progres-
. In all these plots, there is a weak magnetic field acting transverse to the disk (M = 0.2). Increasing g serves to elevate the radial velocity (at or near the disk surface), but strongly decelerates the tangential flow, both at the disk surface and through the boundary layer regime. The shear-driven flow (figure 10) in the tangential (azimuthal) direction, g, is progres-
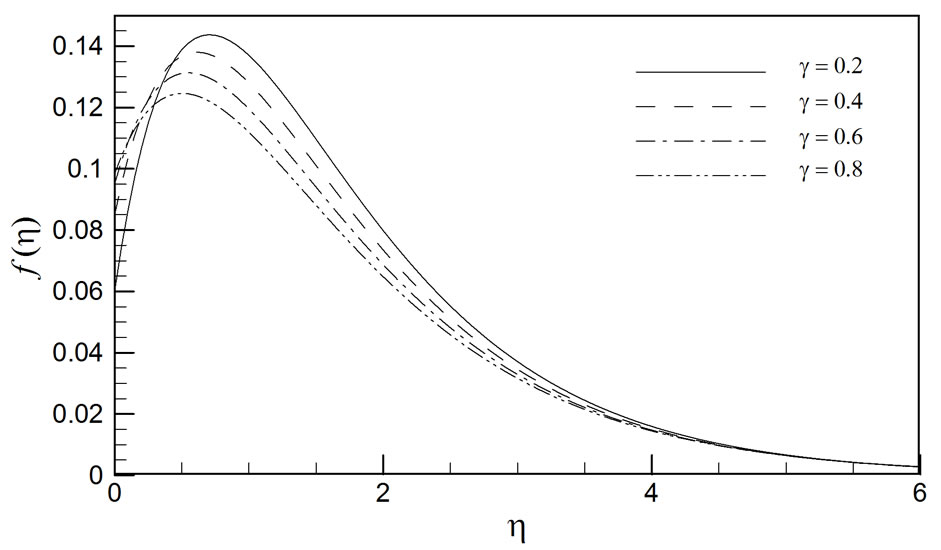
Figure 9. Influence of γ (slip parameter) on the radial velocity profiles (M = 0.2, Ec = 0.2, Du = 0.06, Sc = 0.2, Sr = 1, Pr = 0.71).
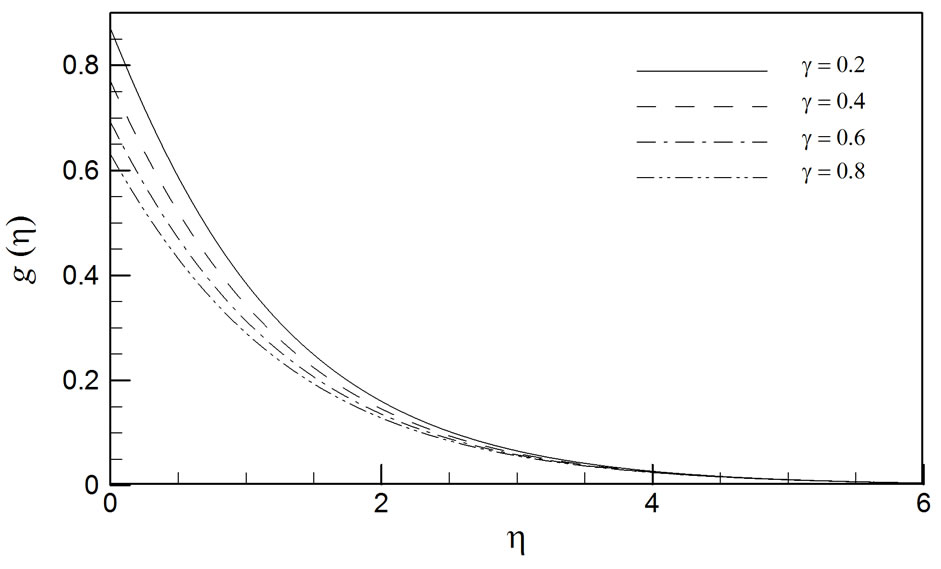
Figure 10. Influence of γ (slip parameter) on the tangential (azimuthal) velocity profiles (M = 0.2, Ec = 0.2, Du = 0.06, Sc = 0.2, Sr = 1, Pr = 0.71).

Figure 11. Influence of γ (slip parameter) on the axial velocity profiles (M = 0.2, Ec = 0.2, Du = 0.06, Sc = 0.2, Sr = 1, Pr = 0.71).

Figure 12. Influence of γ (slip parameter) on the temperature profiles (M = 0.2, Ec = 0.2, Du = 0.06, Sc = 0.2, Sr = 1, Pr = 0.71).

Figure 13. Influence of γ (slip parameter) on the concentration profiles, (M = 0.2, Ec = 0.2, Du = 0.06, Sc = 0.2, Sr = 1, Pr = 0.71).
sively retarded with increasing wall slip parameter. Flow reversal however is never generated anywhere in the boundary layer for the radial and tangential velocity profiles i.e. values are sustained as positive. Axial velocity, h, is observed in figure 11, to be consistently negative, irrespective of the value of the slip parameter. However with increasing g the axial flow is infact accelerated i.e. values of h become more positive. The radial outflow is balanced by an axial inflow towards the rotating disk i.e. the system acts as a fan drawing fluid in. As the radial flow is suppressed, the axial flow will compensate for this and will be accelerated. Both temperature (figure 12) and concentration (figure 13) are elevated by an increase in the wall slip parameter. These results computed with DTM-Padé approach again concur with the shooting computations of Osalusi et al. [19], and the network simulation solutions by Bég et al. [45], again testifying to the accuracy of the DTM-Padé analytical procedure.
Finally in figures 14-18, the effects of the magnetic parameter (M) on the radial velocity (f), tangential velocity (g), axial velocity (h), temperature (q) and concentration (j) profiles, are depicted. 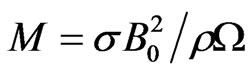 characterizes the relative influence of the hydromagnetic drag force to the rotational (Coriolis) body force in the regime. M > 1 implies that hydromagnetic drag is dominant and M < 1 implies that rotational hydrodynamic force is dominant. For the special case of M = 1, both magnetohydrodynamic body force and rotational body force will have the same order of magnitude. M features in the momentum conservation equations (10) and (11) and the heat conserva-
characterizes the relative influence of the hydromagnetic drag force to the rotational (Coriolis) body force in the regime. M > 1 implies that hydromagnetic drag is dominant and M < 1 implies that rotational hydrodynamic force is dominant. For the special case of M = 1, both magnetohydrodynamic body force and rotational body force will have the same order of magnitude. M features in the momentum conservation equations (10) and (11) and the heat conserva-

Figure 14. Influence of M (magnetic parameter) on the radial velocity profiles, (γ = 0.2, Ec = 0.2, Du = 0.06, Sc = 0.2, Sr = 1, Pr = 0.71).
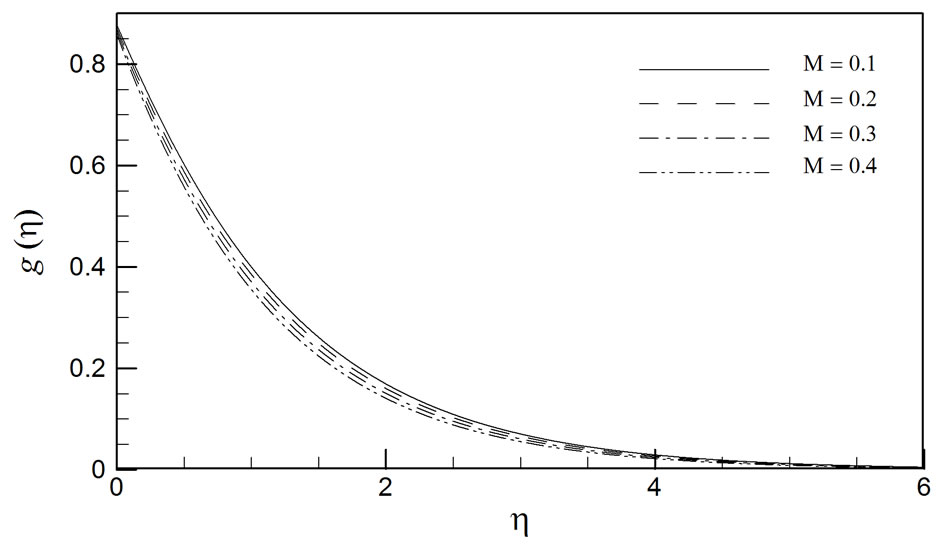
Figure 15. Influence of M (magnetic parameter) on the tangential velocity profiles, (γ = 0.2, Ec = 0.2, Du = 0.06, Sc = 0.2, Sr = 1, Pr = 0.71).
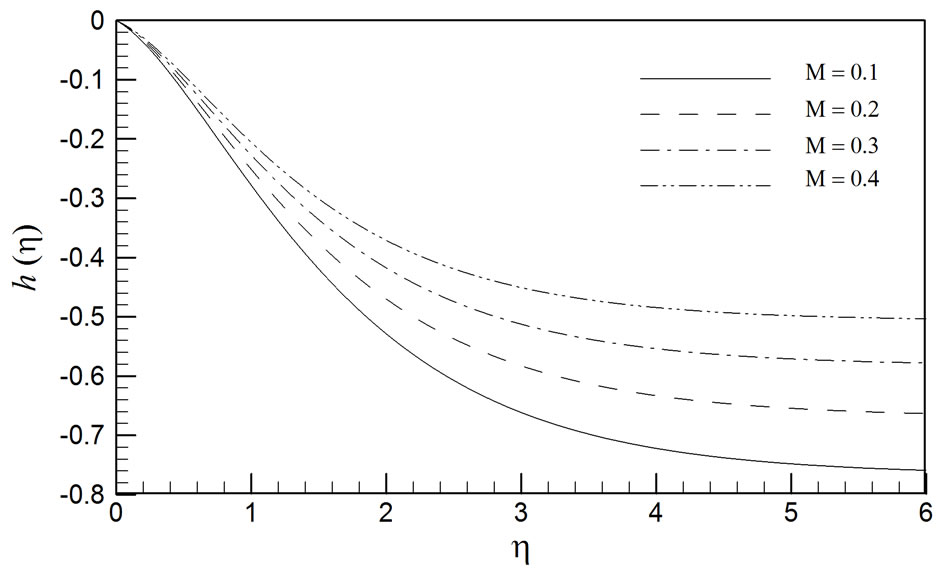
Figure 16. Influence of M (magnetic parameter) on the axial velocity profiles, (γ = 0.2, Ec = 0.2, Du = 0.06, Sc = 0.2, Sr = 1, Pr = 0.71).

Figure 17. Influence of M (magnetic parameter) on the temperature profiles, (γ = 0.2, Ec = 0.2, Du = 0.06, Sc = 0.2, Sr = 1, Pr = 0.71).

Figure 18. Influence of M (magnetic parameter) on the concentration profiles, (γ = 0.2, Ec = 0.2, Du = 0.06, Sc = 0.2, Sr = 1, Pr = 0.71).
tion (energy) equation (12). In equations (10) and (11), the Lorentzian magnetohydrodynamic drag terms, –Mf and –Mg, are linear. An increase in M will therefore elevate these hydromagnetic drag forces and will act to impede the radial (figure 14) and tangential (figure 15) velocities i.e. decelerate both the radial and azimuthal flow. Conversely since the applied magnetic field acts along the negative direction of the axis normal to the disk surface i.e. in the reverse h-direction (or z-direction), it will not exert a component in the axial direction (the Lorentian force acts only at right angles (i.e. transversely) to the direction of the applied magnetic field, B0). The destruction in radial and azimuthal (tangential) momentum is compensated for by a significant boost in axial momentum. In consistency with this, we observe in figure 16 that although h values are always negative (indicating flow reversal in the axial direction), they become increasingly positive with greater M values. Hence magnetic field serves to stifle axial backflow and accelerate the flow. This trend has significant potential in magnetohydrodynamic disk energy generators and also in chemical engineering operations involving transverse magnetic fields, since the flow can be retarded effectively in the radial and tangential directions, and simultaneously enhanced in the axial direction, with the imposition of a static transverse magnetic field. In figures 17 and 18 it is evident also that temperature and concentration are strongly elevated with an increase in magnetic parameter, M. With the action of radial and azimuthal Lorentzian hydromagnetic drag forces, extra work is required to drag the fluid against the action of the magnetic field. This supplementary work is dissipated as thermal energy which causes a heating of the boundary layer regime i.e. elevation in temperatures. This effect also induces greater species diffusion in the regime and elevates the concentration in the boundary layer regime adjacent to the rotating disk. In chemical materials mixing/processing operations, therefore a stronger magnetic field will enhance concentration distributions which may be required to alter the constitution of the final product.
7. Conclusions
In this paper, the DTM-Padé semi-analytical procedure has been employed to investigate combined heat and mass transfer of a steady MHD convective and slip flow due to a rotating disk with viscous dissipation, Ohmic heating, Soret and Dufour effects. The DTM technique combined with Padé approximants has been shown to be very accurate at solving the complex nonlinear differenttial equations describing the flow. DTM-Padé methodology therefore holds significant promise for nonlinear flow dynamics problems in process mechanical engineering. The method has been applied directly without requiring linearization, discretization, or perturbation. The obtained results demonstrate the reliability of the algorithm and encourage its application to other flow domains, such as non-Newtonian systems which are generally nonlinear. The results have also shown that with an increase in magnetic parameter (M), radial velocity is suppressed and tangential velocity is decreased, whereas axial velocity is elevated. Increasing Eckert number (Ec i.e. dissipation parameter) is found to elevate temperatures in the boundary layer but exerts a negligible effect on concentrations. Increasing Soret number (Sr) acts to enhance concentration distributions. With inscreasing wall slip parameter (g), radial velocity is shown to be accelerated near the disk surface and axial velocity is also elevated, whereas the tangential velocity is consistently decelerated. Furthermore there is a strong increase in temperature and concentration values in the boundary layer regime with increasing wall slip parameter. The current problem has been confined to steady flow. Future studies will examine transient rotating disk flows and also consider a variety of rheological flow and nanofluid models [47]; the results of these investigations utilizing the DTM-Padé will be communicated imminently. Extensive validation of the DTM-Padé seminumerical code developed by the authors is described also in [47].
8. Acknowledgements
The authors wish to express their gratitude to the reviewer for his useful comments which have helped to improve the present article.
REFERENCES
- P. O. Tsatsin and V. P. Beskachko, “The Influence of Magnetic Field on the Inertial Deposition of a Particle on a Rotating Disk,” 13th International Conference on Liquid and Amorphous Metals: Special Volume, Journal of Physics: Conference Series, Vol. 98, 2008, pp. 1-4.
- A. Arikoglu, I. Ozkol and G. Komurgoz, “Effect of Slip on Entropy Generation in a Single Rotating Disk in MHD Flow,” Applied Energy, Vol. 85, No. 12, 2008, pp. 1225- 1236. doi:10.1016/j.apenergy.2008.03.004
- E. A. Salem, M. F. Khalil and S. A. Hakim, “Thermohydrodynamic Lubrication of Rotating Magnetohydrodynamic Thrust Bearings,” Wear, Vol. 62, No. 2, 1980, pp. 337-348. doi:10.1016/0043-1648(80)90178-7
- J. Zueco and O. A. Bég, “Network Numerical Analysis of Hydromagnetic Squeeze Film Flow Dynamics between Two Parallel Rotating Disks with Induced Magnetic Field Effects,” Tribology International, Vol. 43, No. 3, 2010, pp. 532-543. doi:10.1016/j.triboint.2009.09.002
- G. Hinds, F. E. Spada, J. M. D. Coey, T. R. N. Mhíocháin and M. E. G. Lyons, “Magnetic Field Effects on Copper Electrolysis,” Journal of Physical Chemistry B, Vol. 105, No. 39, 2001, pp. 9487-9502. doi:10.1021/jp010581u
- R. Bessaih, P. Marty and M. Kadja, “Numerical Study of Disk Driven Rotating MHD Flow of a Liquid Metal in a Cylindrical Enclosure,” Acta Mechanica, Vol. 135, No. 3-4, 1999, pp. 153-167. doi:10.1007/BF01305749
- N. Harada, H. Yamasaki and S. Shioda, “High Enthalpy Extraction from a Helium-Driven Disk Magnetohy-drodynamic Generator,” American Institute of Aeronautics and Astronautics (AIAA) Journal of Propulsion and Power, Vol. 5, No. 3, 1989, pp. 353-357. doi:10.2514/3.23160
- A. Liberati and Y. Okuno, “Influence of Anode-Region Boundary-Layer Separation on Disk MHD-Generator Performance,” IEEE Transactions on Plasma Science, Vol. 35, No. 5, 2007, pp. 1588-1597. doi:10.1109/TPS.2007.904955
- P. Intani, T. Sasaki, T. Kikuchi and N. Harada, “Analysis of Disk AC MHD Generator Performance by Finite Element Method,” Journal of Plasma Fusion Research (Japan), Vol. 9, 2010, pp. 580-585.
- A. L. Aboul-Hassan and H. A. Attia, “Flow Due to a Rotating Disk with Hall Effect,” Physics Letters A, Vol. 228, No. 4-5, 1997, pp. 286-290. doi:10.1016/S0375-9601(97)00086-8
- M. Turkyilmazoglu, “Heat and Mass Transfer on the Unsteady Magnetohydrodynamic Flow Due to a Porous Rotating Disk Subject to a Uniform Outer Radial Flow,” American Society of Mechanical Engineers (ASME) Journal of Heat Transfer, Vol. 132, 2010, pp. 1-6.
- A. Postelnicu, “Influence of a Magnetic Field on Heat and Mass Transfer by Natural Convection from Vertical Surfaces in Porous Media Considering Soret and Dufour Effects,” International Journal of Heat and Mass Transfer, Vol. 47, 2004, pp. 1467-1472. doi:10.1016/j.ijheatmasstransfer.2003.09.017
- R. Bhargava, R. Sharma and O. A. Bég, “Oscillatory Chemically-Reacting MHD Free Convection Heat and Mass Transfer in a Porous Medium with Soret and Dufour Effects: Finite Element Modeling,” Inernational Journal of Applied Mathematics and Mechanics, Vol. 5, 2009, pp. 15-37.
- O. A. Bég, A. Y. Bakier and V. R. Prasad, “Numerical Study of Free Convection Magnetohydrodynamic Heat and Mass Transfer from a Stretching Surface to a Saturated Porous Medium with Soret and Dufour Effects,” Computational Materials Science, Vol. 46, No. 1, 2009, pp. 57-65. doi:10.1016/j.commatsci.2009.02.004
- K. A. Maleque and M. A. Sattar, “Similarity Solution of MHD Free-Convective and Mass Transfer Flow over an Vertical Porous Plate with Thermal Diffusion Effects,” Arabian Journal of Science Engineering, Vol. 1, 2002, pp. 44-55.
- H. A. Attia, “On the Effectivness of Ion Slip and Uniform Suction or Injection on Steady MHD Flow Due to a Rotating Disk with Heat Transfer and Ohmic Heating,” Chemical Engineering Communications, Vol. 194, No. 10, 2007, pp. 1396-1407. doi:10.1080/00986440701401545
- J. Zueco, O. A. Bég, H. S. Takhar and V. R. Prasad, “Thermophoretic Hydromagnetic Dissipative Heat and Mass Transfer with Lateral Mass Flux, Heat Source, Ohmic Heating and Thermal Conductivity Effects: Network Simulation Numerical Study,” Applied Thermal Engineering, Vol. 29, 2009, pp. 2808-2815. doi:10.1016/j.applthermaleng.2009.01.015
- O. A. Bég, J. Zueco and H. S. Takhar, “Unsteady Magnetohydrodynamic Hartmann-Couette Flow and Heat Transfer in a Darcian Channel with Hall Current, Ionslip, Viscous and Joule Heating Effects: Network Numerical Solutions,” Comunication Nonlinear Science Numerical Simulation, Vol. 14, No. 4, 2009, pp. 1082-1097. doi:10.1016/j.cnsns.2008.03.015
- E. Osalusi, J. Side and R. Harris, “Thermal-Diffusion and Diffusion-Thermo Effects on Combined Heat and Mass Transfer of a Steady MHD Convective and Slip Flow due to a Rotating Disk with Viscous Dissipation and Ohmic Heating,” International Communications in Heat and Mass Transfer, Vol. 35, 2008, pp. 908-915. doi:10.1016/j.icheatmasstransfer.2008.04.011
- P. Sibanda and O. D. Makinde, “On Steady MHD Flow and Heat Transfer Past a Rotating Disk in a Porous Medium with Ohmic Heating and Viscous Dissipation,” International Journal of Numerical Methods Heat Fluid Flow, Vol. 20, No. 3, 2010, pp. 269-285.
- M. M. Rashidi, M. Keimanesh, O. A. Bég and T. K. Hung, “Magnetohydrodynamic Biorheological Transport Phenomena in a Porous Medium: A Simulation of Magnetic Blood Flow Control and Filtration,” International Journal for Numerical Methods in Biomedical Engineering, Vol. 27, 2011, pp. 805-821. doi:10.1002/cnm.1420
- J. K. Zhou, “Differential Transformation and Its Applications for Electrical Circuits,” Huazhong University Press, Wuhan, 1986.
- M. M. Rashidi and S. Dinarvand, “Purely Analytic Approximate Solutions for Steady Three-Dimensional Problem of Condensation Film on Inclined Rotating Disk by Homotopy Analysis Method,” Nonlinear Analysis Real World Applications, Vol. 10, No. 4, 2009, pp. 2346-2356. doi:10.1016/j.nonrwa.2008.04.018
- A. Mehmood, A. Ali, H. S. Takhar, O. A. Bég, M. N. Islam and L. S. Wilson, “Unsteady Von Kármán Swirling Flow: Analytical Study Using the Homotopy Method,” International Journal of Applied Mathematics and Mechanics, Vol. 6, 2010, pp. 67-84.
- M. M. Rashidi, D. D. Ganji and S. Dinarvand, “Explicit Analytical Solutions of the Generalized Burger and Burger-Fisher Equations by Homotopy Perturbation Method,” Numerical Methods for Partial Differential Equations, Vol. 25, No. 2, 2009, pp. 409-417. doi:10.1002/num.20350
- A. Rajabi, D. D. Ganji and H. Taherian, “Application of Homotopy Perturbation Method in Nonlinear Heat Conduction and Convection Equations,” Physics Letters A, Vol. 360, No. 4-5, 2007, pp. 570-573. doi:10.1016/j.physleta.2006.08.079
- M. M. Rashidi and E. Erfani, “New Analytical Method for Solving Burgers’ and Nonlinear Heat Transfer Equations and Comparison with HAM,” Computer Physics Communications, Vol. 180, No. 9, 2009, pp. 1539-1544. doi:10.1016/j.cpc.2009.04.009
- C. K. Chen and S. H. Ho, “Applications of the Differential Transform to Eigenvalue Problems,” Applied Mathematics and Computation, Vol. 79, No. 2-3, 1996, pp. 173- 188. doi:10.1016/0096-3003(95)00253-7
- V. S. Erturk, “Differential Transformation Method for Solving Differential Equations of Lane-Emden Type,” Mathematical and Computational Applications, Vol. 12, 2007, pp. 135-139.
- V. S. Erturk, “Application of Differential Transformation Method to Linear Sixth-Order Boundary Value Problems,” Applied Mathematical Sciences, Vol. 1, 2007, pp. 51-58.
- M. M. Rashidi and E. Erfani, “Travelling Wave Solutions of WBK Shallow Water Equations by Differential Transform Method,” Advances in Theoretical and Applied Mechanics, Vol. 3, 2010, pp. 263-271.
- J. Biazar and F. Mohammadi, “Application of Differential Transform Method to the Sine-Gordon Equation,” International Journal of Nonlinear Science, Vol. 10, 2010, pp. 190-195.
- S. Catal, “Solution of Free Vibration Equations of Beams on Elastic Soil by Using Differential Transform Method,” Applied Mathematical Modelling, Vol. 32, No. 9, 2008, pp. 1744-1757. doi:10.1016/j.apm.2007.06.010
- Y. Keskin and G. Oturanc, “Numerical Solution of Regularized Long Wave Equation by Reduced Differential Transform Method,” Applied Mathematical Sciences, Vol. 4, 2010, pp. 1221-1231.
- L. T. Yu and C. K. Chen, “The Solution of the Blasius Equation by the Differential Transformation Method,” Mathematical and Computer Modelling, Vol. 28, No. 1, 1998, pp. 101-111. doi:10.1016/S0895-7177(98)00085-5
- S. H. Ho and C. K. Chen, “Free Transverse Vibration of an Axially Loaded Non-Uniform Spinning Twisted Timoshenko Beam Using Differential Transform,” International Journal of Mechanical Sciences, Vol. 48, 2006, pp. 1323-1331. doi:10.1016/j.ijmecsci.2006.05.002
- H. P. Chu and C. Y. Lo, “Application of the Hybrid Differential Transform-Finite Difference Method to Nonlinear Transient Heat Conduction Problems,” Numerical Heat Transfer, Part A, Vol. 53, No. 3, 2008, pp. 295-307. doi:10.1080/10407780701557931
- G. A. Baker and P. Graves-Morris, “Padé Approximants,” Encyclopedia of Mathematics and Its Application 13, Parts I and II, Addison-Wesley Publishing Company, New York, 1981.
- G. A. Baker, “Essential of Padé Approximants,” Academic Press, London, 1975.
- M. M. Rashidi and G. Domairry, “New Analytical Solution of the Three-Dimensional Navier-Stokes Equations,” Modern Physics Letters B, Vol. 23, No. 26, 2009, pp. 3147-3155. doi:10.1142/S0217984909021193
- M. M. Rashidi, “The Modified Differential Transform Method for Solving MHD Boundary-Layer Equations,” Computer Physics Communications, Vol. 180, No. 11, 2009, pp. 2210-2217. doi:10.1016/j.cpc.2009.06.029
- M. M. Rashidi and E. Erfani, “A Novel Analytical Solution of the Thermal Boundary-Layer over a Flat Plate with a Convective Surface Boundary Condition Using DTM-Padé,” International Conference on Applied Physics and Mathematics (ICAPM), Singapore, 2009.
- B. Gebhart and L. Pera, “The Nature of Vertical Natural Convection Flow from the Combined Buoyancy Effects on Thermal and Mass Diffusion,” International Journal of Heat and Mass Transfer, Vol. 14, No. 12, 1971, pp. 2025-2040. doi:10.1016/0017-9310(71)90026-3
- M. Gad-el-Hak, “The Fluid Mechanics of Microdevices: The Freeman Scholar Lecture,” ASME―Journal of Fluids Engineering, Vol. 121, No. 1, 1999, pp. 5-33. doi:10.1115/1.2822013
- O. A. Bég, J. Zueco and L. M. Lopez-Ochoa, “Network Numerical Analysis of Optically-Thick Hydromagnetic Slip Flow from a Porous Spinning Disk with Radiation Flux, Variable Thermophysical Properties, and Surface Injection Effects,” Chemical Engineering Communications, Vol. 198, No. 3, 2010, pp. 360-384. doi:10.1080/00986445.2010.512543
- H. Schlichting, “Boundary-Layer Theory,” 7th Edition, MacGraw-Hill, New York, 1979.
- M. M. Rashidi, O. Anwar Bég, M. Asadi and M. T. Rastegari, “DTM-Padé Modeling of Natural Convective Boundary Layer Flow of a Nanofluid Past a Vertical Surface,” International Journal of Thermal & Environmental Engineering, Vol. 4, 2012, pp. 13-24. (in press)
Appendix 1

Table 1. The fundamental operations for the one-dimensional Differential Transform Method (DTM).

