World Journal of Mechanics
Vol. 1 No. 3 (2011) , Article ID: 5770 , 5 pages DOI:10.4236/wjm.2011.13011
An Investigation into the Effect of Porous Medium on Performance of Heat Exchanger
1The member of scientific board of Islamic azad university (sofian branch)
2The member of scientific board of Islamic azad university (sofian branch)
E-mail: hadi_dehgan2001@yahoo.com, peiman-aliparast@tabrizu.ac.ir
Received February 19, 2011; revised April 22, 2011; accepted May 3, 2011
Keywords: Porous Medium, Forced Convection, Fluent, Heat Exchanger, Laminar Flow
ABSTRACT
In this paper, a detailed numerical investigation of two-dimensional laminar forced convection in a porous channel with inlet and outlet slot is presented. A uniform heat flux is applied on one wall of channel and another wall is isolated. The flow in the porous medium is modeled using the Brinkman-Forchheimer-extended Darcy model in which the inertia and boundary effects are taken into consideration and thermal dispersion effects are not included in the energy equation. Parametric studies are conducted to evaluate the effects of particle diameter, Reynolds number on the heat transfer and friction factor. Nusselt number and friction factor are developed for efficient design of a porous heat exchanger based on the present configuration. In order to solve this problem Fluent software was used.
1. Introduction
Recent advances in high-technology fields such as electronic system have lead to dramatic increases in heat flux levels, for thermal management of such systems, more efficient heat transfer enhancement techniques are being explored. There has been a growing interest in heat transfer enhancement using a porous medium and several studies have reported that the use of porous medium for heat transfer yields higher heat transfer performance than existing techniques such an pinned-fin array or twisted tape inserts. Hunt and Tien [1] experimentally studies forced convection through a fibrous medium and showed that with high permeability porous materials, heat transfer enhancement of up to four times higher than without the porous medium could be achieved mainly due to higher thermal dispersion effects. Kuzay [2] investigated heat transfer enhancement using metal-wool filled tubes. Hwang and Chao [3] conducted experiments and numerical simulation for the heat transfer behavior of sintered metallic materials. Hadim [4] considered discrete porous bands in a channel with discrete heat source on one wall. Vafai [5] considered discrete porous blocks on one wall of a rectangular channel. These studies demonstrated that with proper selections of governing parameters and different geometric structures of porous medium, could increase rate of heat transfer and reduced pressure drop. on the other hand, several studies concentrated on the physical properties of working fluids for heat transfer enhancement in the presence of porous media. Suzan and Vafai [6] who discussed heat transfer and pressure drop in a porous medium and fluid thermo physical properties as well as geometrical configurations. Chen and Hadim [7] described by the power-law model in a channel filled with packed spherical particles. Their results indicate that shear thinning fluid result in higher heat transfer and reduced pressure drop than Newtonian fluids in porous media. Leong and Jin [8] studied forced convection heat transfer in a channel with different configuration of graphite foams. Marcelo [9] defined laminar heat transfer in a porous channel simulated with a two-energy equation model.
In the present study, a porous parallel-plate channel containing a fluid-saturated sintered porous metal matrix that a uniform heat flux is applied on one of the walls and another wall of channel is isolated. To perform a detailed study of the hydrodynamic and heat transfer characteristics within porous channel, the numerical model for a steady-state, incompressible, and two-dimensional flow in metal porous channel is developed. The flow in the porous medium is modeled using the brinkman-forchheimerextended Darcy model that takes into account the boundary and inertia effects, thermal dispersion are neglected in the energy equation. Channeling effects near the walls are neglected in the present model and porosity is assumed to be constant. The numerical model is validated by comparing the present numerical results with the experimental data. Geometrical configuration of channel is shown in Figure 1.
2. Nomenclature
Cf = inertia coefficient
h = heat transfer coefficient
K = permeability of porous medium
Dp = particle diameter
Nu = nusselt number
k = thermal conductivity
Dh = hydraulic diameter
F = friction factor
T = temperature
P = pressure
q” = heat flux
u = fluid velocity along x-direction
v = transverse fluid velocity along the duct height
Greek symbols
µ = dynamics viscosity of the fluid
 = fluid density
= fluid density
 = porosity
= porosity
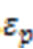 = performance parameter
= performance parameter
Subscripts
f = fluid
s = solid
w = wall
o = inlet
e = effective
3. Mathematical Formulation
A schematic configuration of the physical model of porous channel is illustrated in Figure 1. This configuration is based on the design of new pumped single-phase porous metal heat exchanger consisting of a porous matrix bonded between the heat exchanger faceplate and a subtract with coolant injection and removal ports. The

Figure 1. Schematic configuration of the physical model.
porous medium is composed of sintered metal particles such as aluminum spherical beads. Steady state, incompressible, and two-dimensional flow in a channel filled with a homogeneous and isotropic sintered porous metal and heated from the bottom wall is considered. Channeling effects near the walls are neglected in the present model and porosity is assumed to be constant. The thermo physical properties of fluid (water) and of the porous medium are assumed to be constant. Based on the physical model discussed above, the governing equation can be written as:
Continuity equation: considering a laminar, incompressible Newtonian fluid flow, the conservation equation of mass is derived as:
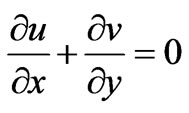 (1)
(1)
Momentum equation: the microscopic momentum equation are given by the navier-stokes equation:
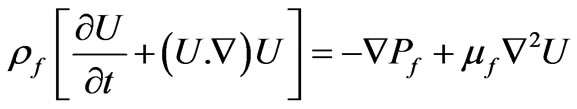 (2)
(2)
Similarly, integrating equation (2) with respect to a REV (representation volume) and the no-slip condition on the solid surface gives:
 (3)
(3)
For steady-state situations, dividing by 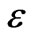 on both sides of Equation (3) leads to:
on both sides of Equation (3) leads to:
 (4)
(4)
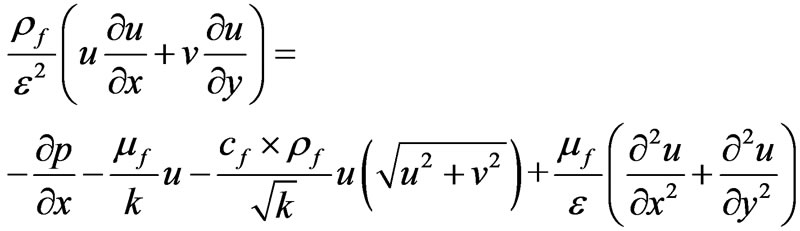 (5)
(5)
That in the momentum equation Darcy term, brinkman term and forchheimer term is calculated in respect with
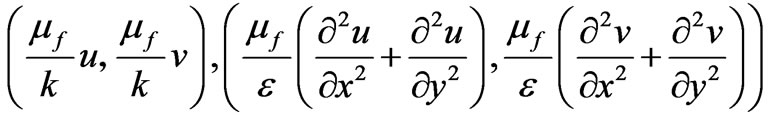
and 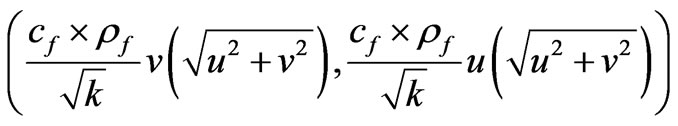
The permeability K and the inertia coefficient Cf are evaluated with using following empirical correlations:
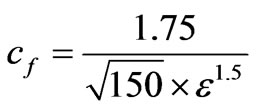 (6)
(6)
And
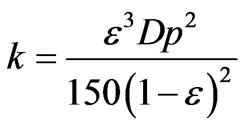 (7)
(7)
Because of local equilibrium between fluid and solid phases in porous media, we have:
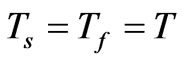
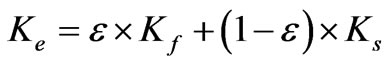
Ke is the effective thermal conductivity.
The boundary conditions for the configuration considered are as follows: no slip condition occurs on all the solid surface (top and bottom walls), the velocity v and temperature T of flow are uniform over the cross section of the inlet port. The dimensionless averaged pressure difference between the inlet and outlet ports is calculated in terms of the friction factor which is defined as:
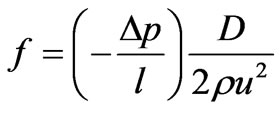
The local Nusselt number for the heated boundary is defined as:
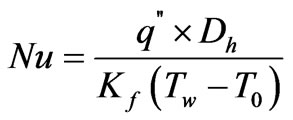
4. Numerical Procedure
The governing equation (1-5) with the associated boundary condition was solved numerically utilizing a control volume method. The momentum equation for velocity and pressure drop was solved first and the energy equation for temperature and heat transfer rate was then solved based on the corrected velocity results. After a staggered grid was arranged for the discretization process a second—order upwind was employed to model the interaction between the convection and the diffusion terms in governing equations. An iterative procedure based on the Simple algorithm was employed to deal with the linkage between pressure and velocity in the momentum equations, and temperature in the energy equation. In order to solve this problem with all considered boundary conditions was used. But because doesn’t include equations related to terms of brinkman and forchheimer ,we add up these equations using udf (user defined function) to fluent but before solving this problem using fluent, geometrical configuration are meshed with gambit software. Gambit is the preprocessing software for fluent used for creating and meshing 2-d model. The units are not important while creating the grid in gambit, but the simulation in fluent always requires the input parameters to be in S.I units. For 2-d geometers, the z-coordinate is assigned a default value of zero. Both structured and unstructured meshes are available in gambit. in the present study, structured meshing was employed. Boundary conditions types for inlet, outlet and channel walls were specified and the mesh-file is saved in a binary format for fluent to recognize. In Figure 2 the mesh is created by gambit, was shown.
5. Results and Discussion
To investigate the effects of particle diameter on heat transfer and pressure drop, the particle diameter Dp is selected. It is shown in Figures 3 and 4 that in the relatively small particle diameter region (Darcy regime), the length-averaged Nusselt number (Nu) and the pressure drop (fRe ) decrease sharply with increasing 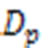 . For a large particle diameter (non-Darcy regime), the nusselt number and the pressure drop both decrease slowly as they approach their corresponding asymptotic values for the nonporous case. As would be expected, a higher heat
. For a large particle diameter (non-Darcy regime), the nusselt number and the pressure drop both decrease slowly as they approach their corresponding asymptotic values for the nonporous case. As would be expected, a higher heat
Figure 2. Schematic configuration of the physical model, mesh is created by gambit.
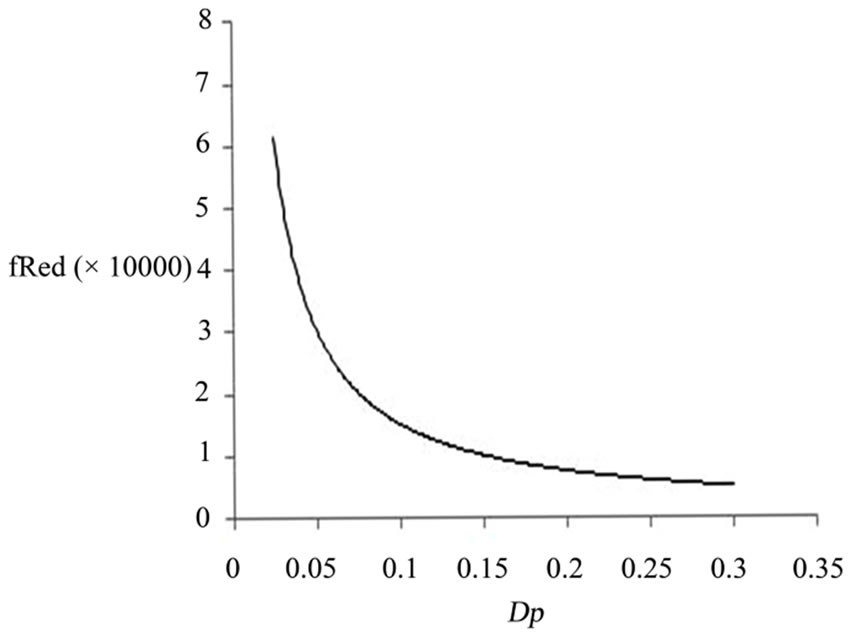
Figure 3. Effects of particle diameter on the dimensional pressure drop in the porous channel.
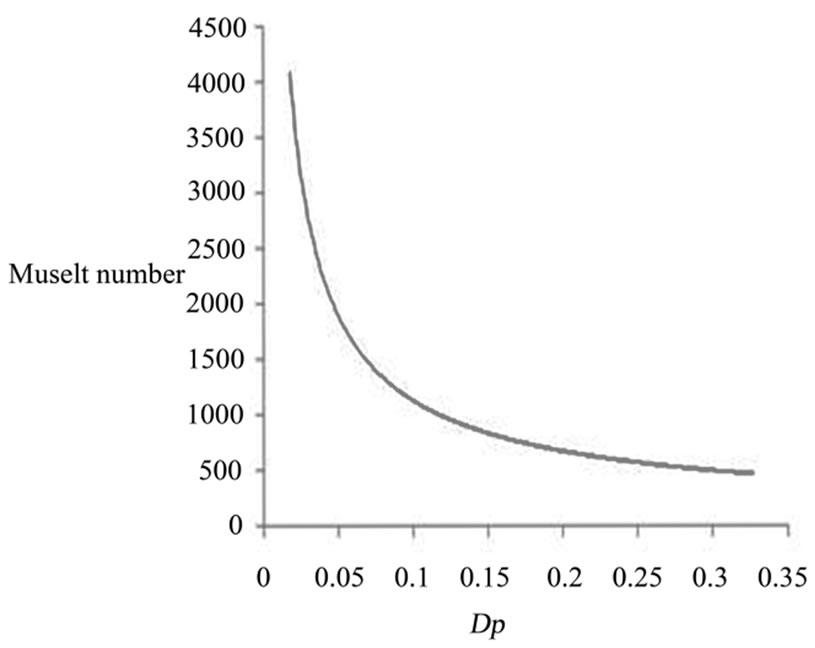
Figure 4. Effects of particle diameter on nusselt number in the porous channel.
transfer rate is achieved at a larger penalty in pressure drop. Although both the Nusselt number and pressure drop increase as the particle diameter decreases, the increasing rates of both parameters are different. For example, as dp decrease from 0.2 to 0.1, the pressure drop increase by 52% but the Nusselt number increase only by 30%. Thus a relatively larger penalty for pressure drop will occur when a smaller particle diameter is selected to enhance heat transfer.
The combined effects of the Reynolds number and the particle diameter on heat transfer are illustrated in Figure 5. As the Reynolds number is increased, the Nusselt number increases, and the porous medium with a smaller particle diameter generates a higher increase in heat transfer enhancement than one with a larger particle diameter. However, as the Reynolds number becomes smaller, the Nusselt number approaches an asymptotic value which is mainly dependent on the particle diameter. As the Reynolds is increased, the pressure drop in the
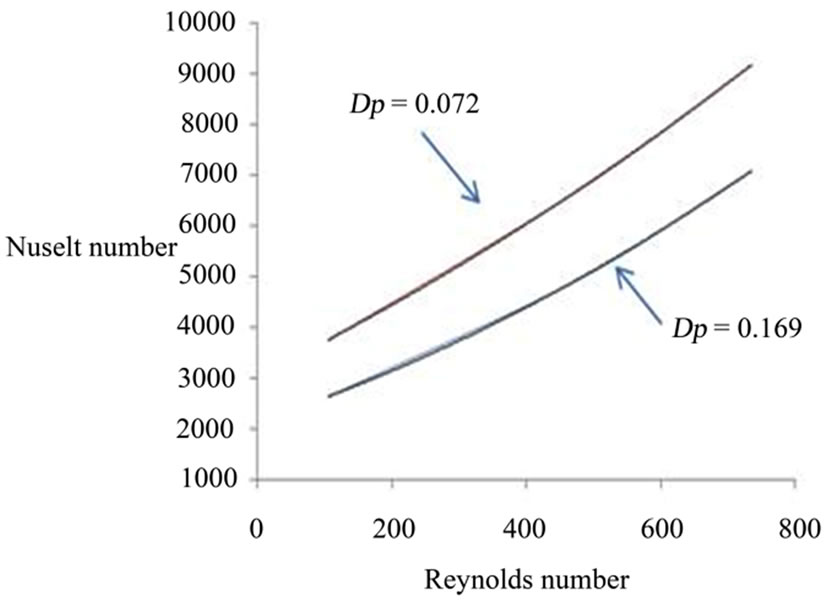
Figure 5. Effects of Reynolds number and particle diameter on the Nusselt number in porous channel.
channel is also increased as discussed earlier.
In the design of heat exchangers in which a porous medium is not present, a dimensionless parameter is usually used to evaluate the performance based on both the heat transfer enhancement and the associated pressure drop. This parameter is defined as:
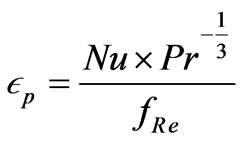
In the present study, a similar parameter is used to evaluate the performance of the porous channel heat exchanger .in Figure 6 and 7 the effects of Reynolds number and particle diameter on the heat exchanger performance parameter are illustrated. as the particle diameter decrease or as the Reynolds number increase , although the heat transfer enhancement increases, the performance parameter decreases since the increasing rate of the dimensionless pressure drop is much higher than that of the nusselt number is illustrated in Figure 8, for example
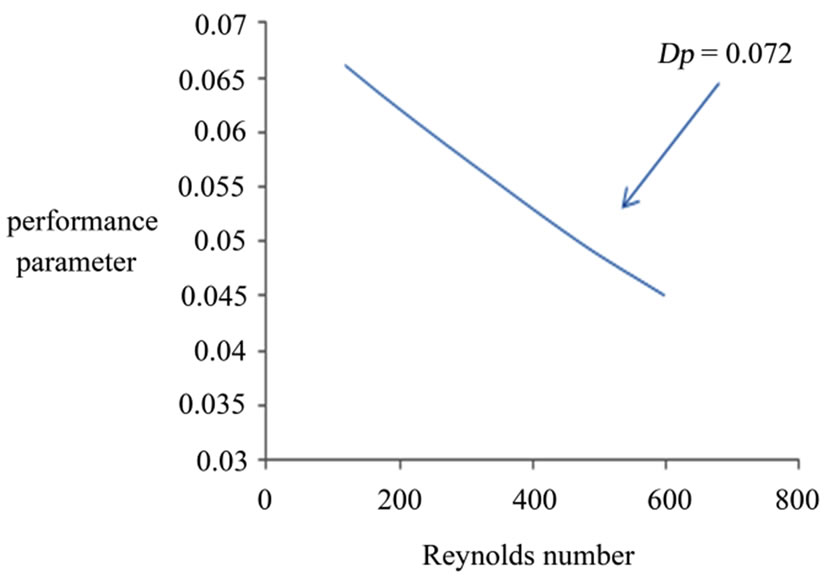
Figure 6. Effect of Reynolds number and particle diameter on performance parameter.

Figure 7. Effect of Reynolds number and particle diameter on performance parameter.
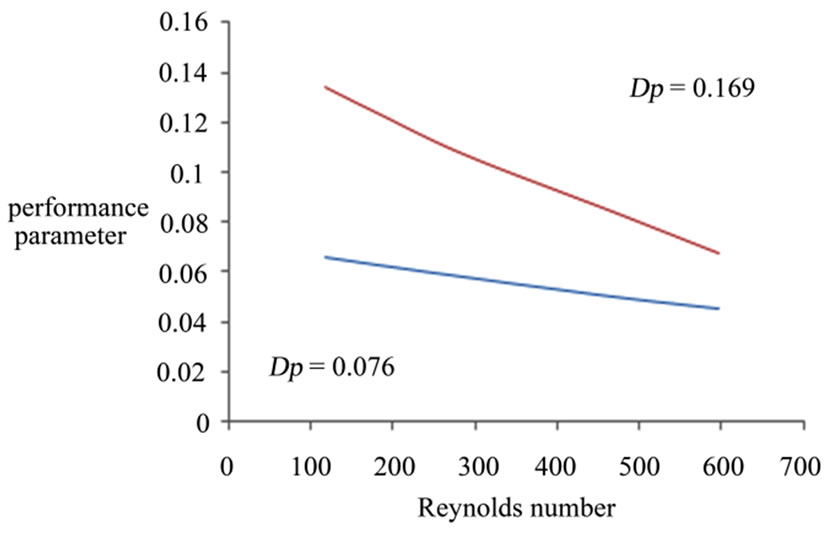
Figure 8. Compration of effect of renolds number and particle diameter on performance parameter.
as Re increases from 180 to 600, performance parameter decrease by 42% for Dp = 0.169, and by only 28% for Dp = 0.072
6. Conclusions
A numerical study of laminar forced convection in a two-dimensional porous channel with inlet and outlet ports was conducted. a smaller particle diameter can be used to achieve higher heat transfer enhancement , but a larger particle diameter leads to a more efficient performance based on heat transfer enhancement.
REFERENCES
- M. L. Hunt and C. L. Tien, “Effect of Thermal Dispersion on Forced Convection in Fibrous Media,” International Journal of Heat Mass Transfer, Vol. 31, No. 2, 1988, pp. 301-309. doi:10.1016/0017-9310(88)90013-0
- T. M. Kuzay, J. T. Collins and A. M. Khounsary, “Enhanced Heat Transfer with Metal-Wood-Filled Tubes,” Proceedings of ASME/JSEM Thermal Engineering Conference, 1991, pp. 451-459.
- G. J. Hwang and C. H. Chao, “Heat Transfer Measurement and Analysis for Sintered Porous Channels,” Journal of Heat Transfer, ASME Transactions, Vol. 116, No. 2, 1994, pp. 456-464. doi:10.1115/1.2911418
- A. Hadim, “Forced Convection in a Porous Channel with Localized Heat Sources,” Journal of Heat Transfer, ASME Transactions, Vol. 116, No. 2, 1994, pp. 465-472. doi:10.1115/1.2911419
- K. Vafai, “Analysis of Forced Convection Enhancement in a Channel Using Porous Block,” AIAA Journal of Thermophysics and Heat Transfer, Vol. 8, pp. 563-573.
- M. Sozen and K. Vafai, “Longitudinal Heat Dispersion in Porous Beds,” AIAA Journal of Heat Transfer, pp. 153-157.
- H. Chen and A. Hadim, “Numerical Study of Non-Darcy Forced Convection in a Packed Bed Saturated with Power –Law Fluid,” Journal of Porous Media, Vol. 1, No. 2, 1998, pp. 147-157.
- K. C. Leong, H. Y. Li, L. W. Jin and J. C. Chai, “Numerical and Experimental Study of Forced Convection in Graphite Foams,” Thermal Engineering, Vol. 30, No. 5, 2010, pp. 520-532. doi:10.1016/j.applthermaleng.2009.10.014
- M. B. Saito and M. J. S. de Lemos, ”Laminarheat Transfer in a Porous Channel Simulated with a Two-Energy Equation Model,” International Communications in Heat and Mass Transfer, Vol. 36, No. 10, 2009, pp. 1002- 1007. doi:10.1016/j.icheatmasstransfer.2009.07.008

