World Journal of Condensed Matter Physics
Vol.06 No.04(2016), Article ID:72088,6 pages
10.4236/wjcmp.2016.64028
On the Thermodynamics of a Two-Dimensional Electron Gas with Non-Parabolic Dispersion
G. Gulyamov1, B. T. Abdulazizov2
1Pedagogical Institute, Namangan, Uzbekistan
2Namangan State University, Namangan, Uzbekistan

Copyright © 2016 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY 4.0).
http://creativecommons.org/licenses/by/4.0/



Received: September 8, 2016; Accepted: November 14, 2016; Published: November 17, 2016
ABSTRACT
A thermodynamic density of states, electron density in the subband and the entropy of the gas as function of the temperature and the total two-dimensional electron density are studied. Semiconductor conduction band dispersion is described by the simplified Kane model. Numerical simulation shows that with an increase in the total electron concentration, thermodynamic density of states at low temperatures changes abruptly and smoothes jumps at high temperatures. This change manifests itself in the peculiar thermodynamic characteristics. The results are used to interpret existing experimental data.
Keywords:
Quantum Well, Two-Dimensional Electron Gas, Kane Model, Subbands Statistics, Entropy

1. Introduction
Recently, a large number of studies are devoted to the study of two-dimensional electron gas in a magnetic field [1] - [3] . Studying influences of other factors as anisotropy of the electron spectrum and conduction band nonparabolicity on the properties of two dimensional electron gas is also important [4] . The results of such studies play an important role for the understanding of the nature of the two-dimensional electron gas: subbands structure, electron statistics in subbands etc.
In work [5] , it analyzes density of states (DOS) of two-dimensional electron gas in a single quantum well (QW) on the base of narrow-gap semiconductors, InAs and InSb. It is shown that the nonparabolicity of conduction band leads to a noticeable change in the DOS of two-dimensional electron gas.
It is known [6] that most of the experimentally observed thermodynamic properties of the electron gas (such as entropy, heat capacity, etc.) are directly determined by the DOS system. Thus, the observed properties of two-dimensional electron gas in a narrow-gap material are primarily determined by the quantization of electron energy and nonparabolicity of conduction band.
This work is devoted to the calculation of the thermodynamic DOS, the concentration of electrons in the subband and the entropy of a gas as a function of total concentration and temperature with allowance for the nonparabolicity of conduction band. It is shown that with increasing total concentration of electrons, thermodynamic DOS changes abruptly, and this leads to a peculiar change in the subband’s concentration and entropy. The results are compared with experimental data on the basis of the electron gas in the quantum well heterostructures, InAs/AlSb.
2. Basic Equations
Consider a QW width L, concluded between the barriers of infinite height.
The energy is measured from the bottom of the bulk semiconductor. Dispersion law of electrons in the conduction band relies on nonparabolicity, and in the simplest case describe by two-band Kane model. In the effective mass approximation, the solution of the Schrödinger equation leads to the following dispersion
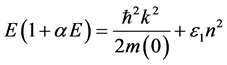 , (1)
, (1)
where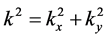 ,
, 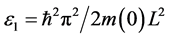 ,
,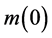 ―electron effective mass at the bottom of the conduction band (in a unit
―electron effective mass at the bottom of the conduction band (in a unit ),
),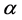 ―parameter nonparabolicity of conduction band.
―parameter nonparabolicity of conduction band.
The total concentration and the concentration of electrons in the subbands defined by the relations
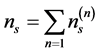 ,
, 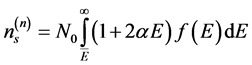 , (2)
, (2)
where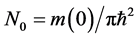 ,
,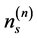 ―concentration n-th subband,
―concentration n-th subband,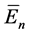 ―solution to Equation (1) in case
―solution to Equation (1) in case ,
,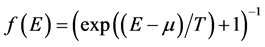 ―the Fermi-Dirac distribution function,
―the Fermi-Dirac distribution function, 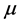 is a chemical potential of electron gas. Equation (2) determine the concentration of electrons in individual subbands
is a chemical potential of electron gas. Equation (2) determine the concentration of electrons in individual subbands 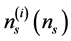 depending on the temperature T and the total concentration
depending on the temperature T and the total concentration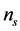 .
.
The thermodynamic DOS is defined as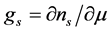 . Given that the
. Given that the 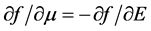 , integrating by parts we obtain the following expression
, integrating by parts we obtain the following expression

The thermodynamic potential 


3. Numerical Results and Discussions
With the help of the relations (2)-(5) can provide useful information about the behavior of the two-dimensional electron gas at varying temperatures and the total electron concentration. Calculations of the density of states and entropy are carried out by the example of InAs semiconductor. Used in the calculation of the band parameters of InAs semiconductor are shown in Table 1.
Since the total concentration





Figure 1 shows the dependence of the DOS 



The graph shows the temperature significantly influences the shape of 




Table 1. Band parameters of InAs.
Figure 1. DOS of electron gas as function of the total two-dimensional electron concentration in the InAs QW: L = 18 nm, T = 4.2, and 100 K, α = 0, 2.27.





Since the thermodynamic quantities―entropy, heat capacity, etc. is directly linked to the DOS, and then these values are also abrupt change.
Figure 2 shows the variation of the electron gas entropy as function of the total two- dimensional electron concentration at T = 70 K, L = 18 nm, in the InAs QW with (solid line) and without of conduction band nonparabolicity (dotted line).
The graph shows that the calculation of the thermodynamic quantities―nonparabo- licity effects are important. For example, at a concentration


Nature jumps in the concentration dependence of

The jump in the concentration dependence 

With the growth of the total concentration of the first miniband is filled first, the
Figure 2. The change of electron gas entropy as function of the total concentration in the InAs QW: L = 18 nm, T = 100 K, α = 0, 2.27.
Figure 3. Filling of i = 1, 2, 3 subbands, depending on the total two-dimensional electron concentration for InAs QW: T = 4.2 K, L = 15 and 18 nm. Symbols―experimental data [7] .
concentration continues to increase linearly until it begins filling the second miniband. When filling in the upper subband starts, a filling of the lower subband is slowing. In graphics appears a fracture. These fractures are caused by an abrupt increase in the DOS.
From Figure 3 it appears that the computed curve with L = 18 nm better coincides with the experimental data compared with L = 15 nm curve. In fact, used in this study model QW with V = ∞ overestimates the energy of the electron.
Our estimates show that if use a real value for the height of the potential barrier (say V ~ 1 eV) the calculated curve with L = 15 nm coincides better with the experimental data for comparison with L = 18 nm curve.
High temperatures and a wide QW leads to intensive filling of overlying subbands. Figure 4 shows the change in the electron density of the first five subband depending on the total two-dimensional concentration at T = 300 K, in InAs QW, L = 22 nm. In this case, the fractures observed at low temperatures (see Figure 3) are blurred due to the thermal broadening of quantum levels.
4. Conclusions
This paper, by using numerical simulation, studied the concentration of electrons in the subbands and the entropy of two-dimensional electron gas, depending on the temperature and the total two-dimensional electron density. To account for the conduction band nonparabolicity in the spectrum (1), a simple Kane model is used.
We have shown that an abrupt change in the DOS with increasing concentration (Figure 1) is shown in the example of the thermodynamic characteristics of the entropy (Figure 2). It was established that in the calculation of the thermodynamic quantities, the role of band nonparabolicity is important.
We also presented numerical results dependences of subbands concentration as
Figure 4. Filling of i = 1, 2, 3, 4, 5 subbands in the InAs QW, depending on the total two-dimen- sional electron concentration: T = 300 K, L = 22 nm.
function of total two-dimensional electron concentration (Figure 3). Stepped changes of the DOS are manifested in the form of fracture. These fractures can be seen clearly in calculated lines (Figure 3) and these lines explain the experimental data [7] . The number of filled subbands increases at the wide QW and high temperatures (Figure 4).
5. Funding
This work was supported by the Scientific and Technical program Republic of Uzbekistan (Grant F2-OT-O-15494).
Cite this paper
Gulyamov, G. and Abdulazizov, B.T. (2016) On the Thermo- dynamics of a Two-Dimensional Electron Gas with Non-Parabolic Dispersion. World Journal of Condensed Matter Physics, 6, 294-299. http://dx.doi.org/10.4236/wjcmp.2016.64028
References
- 1. Zawadzki, W. (1984) Thermodynamics of Two-Dimensional Electron Gas in a Magnetic Field. Springer Series in Solid-State Sciences. 53, 79-85.
http://dx.doi.org/10.1007/978-3-642-82311-4_9 - 2. Vagner, D. (2006) Thermodynamics of Two-Dimensional Electron on Landau Levels. HIT Journal of Science and Engineering A, 3, 102-152.
- 3. Ramos, A.C.A., Farias, G.A. and Almeida, N.S. (2011) Thermodynamics of a Quasi-two Dimensional Electron Gas: Effects of Magnetic Fields, Temperature and Finite Width. Physic E: Low-Dimensional Systems and Nanostructures, 43, 1878-1881.
- 4. Paitya, N. and Ghatak, K.P. (2013) Quantization and Carrier Mass. Reviews in Theoretical Science, 1, 1-141.
http://dx.doi.org/10.1166/rits.2013.1008 - 5. Gulyamov, G., Baymatov, P.J. and Abdulazizov, B.T. (2016) Effect of Temperature and Band Nonparabolicity on Density of States of Two Dimensional Electron Gas. Journal of Applied Mathematics and Physics, 4, 272-278.
http://www.scirp.org/journal/jamp - 6. Askerov, B.M. (1994) Electron Transport Phenomena in Semiconductors. World Scientific, Singapore, 412 p.
http://dx.doi.org/10.1142/1926 - 7. Aleshkin, V.Y., Gavrilenko, V.I., Ikonnikov, A.V., Sadofyev, Y.G., Bird, J.P., Jonhson, S.R. and Zhang, Y.-H. (2005) Cyclotron Resonance in Doped and Undoped InAs/AlSb Heterostructures with Quantum Wells. Semiconductors, 39, 62-66.
http://dx.doi.org/10.1134/1.1852647






