World Journal of Condensed Matter Physics
Vol.05 No.04(2015), Article ID:60981,14 pages
10.4236/wjcmp.2015.54027
Numerical Study of the Higgs Mode in the Heisenberg Antiferromagnet on the Square Lattice
Tomo Munehisa
Faculty of Engineering, University of Yamanashi, Kofu, Japan
Copyright © 2015 by author and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/
Received 27 August 2015; accepted 8 November 2015; published 11 November 2015
ABSTRACT
The Higgs mode is expected to exist in any system with the spontaneous symmetry breaking of the continuous symmetry. We make numerical study about the Higgs mode in the Heisenberg antiferromagnet on the square lattice by the exact diagonalisation approach. Since the Higgs mode can couple with a pair of the Nambu-Goldstone modes, we calculate the dynamical correlation of the two spin operators, employing the finite temperature Lanczos method. Because the lattice size is severely limited, we make a careful discussion on procedures of finding evidences for the Higgs mode by numerical works. By the discussed procedures, we present numerical results for the dynamical correlation at zero temperature. Then we obtain clear evidences for the Higgs mode of the spin-1/2 Heisenberg antiferromagnet on the square lattice.
Keywords:
Higgs Mode, Nambu-Goldstone Mode, Heisenberg Antiferromagnet, Dynamical Correlation, Finite Temperature Lanczos Method
1. Introduction
The spontaneous symmetry breaking (SSB) of the continuous symmetry has been one of the most important concepts and phenomena of the modern physics [1] [2] . It is well known that the SSB induces the massless particle or the gapless mode, which is called the Nambu-Goldstone (NG) particle or mode [3] [4] . In the particle physics for the SSB mechanism we need another particle called the Higgs particle [5] . Recently the Higgs particle has been observed and its property has been confirmed to agree with the prediction of the standard model [6] [7] . However the quest on the Higgs particle has not finished, because many researchers consider that it is not a fundamental object of the underlying Hamiltonian [8] . Therefore we need deep understanding on the Higgs particle. The study of the Higgs mode in the other fields gives some keys for the next stage of its study.
In the condensed matter physics the Higgs mode has been extensively studied recently [9] . One can find many experimental reports on the existence of the Higgs mode. The authors of [10] have showed this mode in a two-dimensional neutral superfluid close to a quantum phase transition. The study of [11] about the material of
, has demonstrated a massive excitation corresponding to longitudinal fluctuations of the magnetic moment. For theoretical discussions on this material, see [12] . Also the experiment in [13] for the BCS superconductor 
film has confirmed the appearance of the collective mode of the order parameter. One should note the experimental evidence for the observation of the superconducting Higgs mode in the charge density wave superconductor 
[14] .
On the other hand theoretical study has been active, especially using the sigma model and other effective models. Its purpose is to find experimental possibilities of observing the Higgs mode [15] - [17] . Another is to understand the role of the Higgs mode near the critical point of the quantum phase transition [18] - [20] .
In this work we would like to study the Higgs mode in the spin-1/2 Heisenberg antiferromagnet on the square lattice [21] . This system has been studied extensively by the spin wave theory [22] as well as by numerical methods such as the quantum Monte Carlo method [23] - [25] and the exact diagonalisation [26] . The spin wave theory is quite successful in describing experimental results on this system. Note that this theory contains the NG modes, but not the Higgs mode. This success of the theory is due to the experimental difficulty of observing the Higgs mode [9] . As a result there are few theoretical works about the Higgs mode in the antiferromagnet.
The first motivation of our study is to find directly the Higgs mode in the quantum antiferromagnet. In this system the Hamiltonian is clearly defined and we have many materials that realize it. Therefore the numerical evidence for the Higgs mode should stimulate researchers to study experimentally as well as theoretically for this new degree of freedom in the condensed matter physics. Another motivation is to investigate how the Higgs mode is induced from the fundamental Hamiltonian. In the particle physics the Higgs particle is the object to constitute the Hamiltonian. By contrast, in the condensed matter physics the Higgs mode is not an object of the Hamiltonian, but the collective mode induced from it. Therefore we should be able to calculate the gap energy and other properties of the Higgs mode without any assumption. For this purpose the Hamiltonian of the Heisenberg antiferromagnet on the two-dimensional lattice is the most suitable because one can investigate it by various methods.
In our study on the Heisenberg antiferromagnet, the most important purpose is to find evidences for the Higgs mode on the finite lattice by the reliable method of the numerical calculations at zero temperature. Also we would like to clarify differences between the Higgs modes in the SU(2) symmetry and those in the U(1) symmetry through the study of the XXZ model [27] .
Since the Higgs mode is an excited state, we calculate the dynamical spin correlation. Here we employ the finite temperature Lanczos method [28] , which is the reliable diagonalisation approach.
In the next section after a brief description of the Higgs mode, we discuss procedures of finding evidences for it in our calculation. Here we emphasize that the Higgs mode is the excited mode and it couples with a pair of the NG-modes. Therefore the Higgs mode should be a resonance in the dynamical correlation of two spin operators. On the infinitely large lattice we can easily judge signals for the resonance. On the finite lattice, however, the numerical study for the resonance is a non-trivial task, because we calculate not continuous, but discrete energy eigen values. By taking this discreteness into account, we suggest four procedures to find the evidences. Numerical results are presented in Section 3. This section is divided to four subsections. In each subsection, we show the evidence for Higgs mode by using each suggested procedure. The final section is devoted to a summary and discussion for future researches.
2. Higgs Mode
The spin-1/2 Heisenberg antiferromagnet on the square lattice is given by
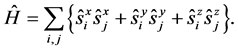(1)
Here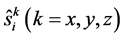
, is a spin operator on a site i and the sum runs over pairs of the neighbor sites on the square lattice. 
is a diagonal matrix, i.e. each state is represented by
, where 
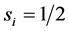or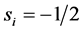
. N is a total number of sites. Since we make an exact diagonalisation by this representation, we can
obtain eigen values of the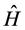 
for a fixed value of a total
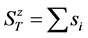, where 
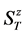is an integer if N is an even
number. For each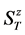 
the lowest energy state is denoted by
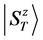. Note that
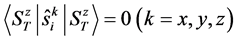, be-
cause the symmetry is not broken on a finite lattice system. In our representation the evidence of the SSB is given by the non-zero value of 
for a finite value of
, where 
is introduced by
(2)
Here we denote a location by 
and
.
From the field theory on the SSB [2] [29] , for the ground state 
we have
(3)
Here 
is the charge, 
is the 0-th component of the current of the continuous symmetry
and 
is the field operator. From the discussion in [2] on (3) we know that there exists a field operator of the NG boson
, which appears in 
and
. If we neglect the higher order products of field operators, we have
(4)
(5)
Here f is the decay constant and Z is the renormalization factor. If we apply the above discussion to the Heisenberg antiferromagnet on the square lattice, we have the following correspondence, as discussed in [29] .
Using the annihilation operator 
and the creation operator 
for the NG mode of the wave vector
, we obtain the correspondences,
(6)
(7)
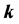
Here 
and 
is the energy of the NG mode with the wave vector
. For another NG mode, we use 
as another current and use 
as the field operator. By the annihilation operator 
and
the creation operator 
for another NG mode of the wave vector
, we have the followings,
(8)
(9)
In the sigma model of the SSB, we have an interaction between the two NG modes and the Higgs mode. In order to obtain a state of the two NG modes, we apply two spin operators of 
to the lowest energy state
. Therefore this application leads us to calculate the dynamical correlation [30] of the two spin operators at zero temperature in order to find the signal for the Higgs mode,
(10)
Here
, 
is the energy eigen value of the state
, 
and
. Since the energy eigen value is discrete on the finite lattice, the delta-function is not well defined. For the definition of the delta-function on this lattice, we use a following function,
with the infinitely small
. Therefore we have a definition for the dynamical correlation on the finite size lattice
(11)
We make 
to be zero after we take the large size limit. Let us consider a simple case of
. In this case we can use a simpler notation for the dynamical correlation,
(12)
If only one resonance state exists as the Higgs mode in the large size limit, we have
(13)
Here
, which does not depend on the wave vector
, is the energy of the Higgs mode, and 
is the width of the resonance. On a finite lattice, however, the Hamiltonian has the discrete eigen values only. For a finite lattice size N, we have
(14)
Here we assume that
. If the limit in (13) exists,
will decrease with the larger N. Based on these considerations
about the Higgs mode on the finite lattice, we propose following four procedures to obtain numerical evidences on the existence of the Higgs mode.
(A) Since we generate the state with the pair of the NG modes from the ground state, which is 
on the finite lattice, we should see peaks in the correlation
. When 
is sufficiently small, we can observe a peak which corresponds with each eigen value. If there are several peaks of
, in a narrow region of
, an observation of these peaks is the basic evidence for the Higgs mode. In following three procedures, we make 
a moderate value in order to examine clusters that are made by several eigen states.
(B) On a lattice of the finite size N we have the lowest energy state 
for each value of
. In the SSB its energy 
agrees with 
for the fixed value of
, when N becomes large, and we could not distinguish between states for 
on the infinitely large lattice. In addition we suppose that a physical quantity depends on 
for the finite N, and the dependence can be expressed by a smooth function of
. For an example, the energy 
is given by
Therefore the Higgs mode must exist on each
, and properties of the Higgs mode should be smooth functions of
. If we observe this existence and these functions in our calculation, this observation is an evidence for the Higgs mode.
(C) On the square lattice, there is the NG mode at 
near 
[29] . Therefore we will find peaks in
as well as peaks in 
when the wave vector 
is near (0,0). If the shape
of the peak in 
is the same as that in
, this observation is also an evidence for the Higgs mode.
(D) We will consider the XXZ model [27] , which has the U(1) symmetry only,
(15)
where
. In this Hamiltonian the conserved current is only
. From the discussion on the correspondence between the current and the field operator of the NG boson, we should find the NG mode at k near (0,0), whereas the excitation at k near T cannot be the NG mode. As a result the peak in 
is not the Higgs mode A numerical evidence for this argument is a clear difference between the peaks of 
in the Heisenberg antiferromagnet and those in the XXZ model.
In the next section we will show the above four evidences through numerical calculations of the dynamical correlation.
3. Numerical Results
In this section we present numerical results of our calculations about the Higgs mode in the Heisenberg antiferromagnet on the finite square lattice. Before presenting results shown in subsections, we describe three steps in calculations of
. The first step is to obtain the eigen state 
with the lowest energy eigen value for each 
by the exact diagonalisation [26] . As the second step, we operate 
to 
in order to make the state that includes the two NG modes of the wave vectors 
and
. Since the state 
contains the contribution of
, we reduce its component from
. Then we obtain the irreducible state,
(16)
Since the magnitude of the 
strongly depends on the lattice size and the wave vector, we will normalize the correlation in order to make a clear comparison among them for the various lattices and the various wave vectors. Therefore we examine the correlation,
(17)
where C is determined for the correlation to satisfy a following normalization,
(18)
The third step of the calculation is to apply the finite temperature Lanczos method [28] [31] [32] by adopting 
as the initial state. Then following the usual Lanczos method, we generate the Lanczos states. The number of these states is fixed to 50, because we see no change in the results when this number is larger than 50. By these Lanczos states we diagonalise the Hamiltonian so that we obtain 
for any value of
.
3.1. Results of the Dynamical Correlation
In this subsection we examine several peaks of the dynamical correlation in the narrow energy region in order to obtain the evidence by the first procedure (A) discussed in the Section 2. First we show results of the dynamical correlation 
for 
on the lattices of N = 20, 26, 32 and 36. The edge vector
are (4,2), (5,1), (4,4) and (6,0) for N = 20, 26, 32 and 36, respectively. Here we impose the 
rotational symmetry to the Hamiltonian. Therefore another edge vector 
is given by
. Note that these edge vectors are defined uniquely for a given lattice size N except for accidental cases. Here
is the non-zero wave vector of the lowest magnitude on the each lattice. They are
, 
, 
and 
for N = 20, 26, 32 and 36, respectively.
Figure 1 shows the dynamical correlation 
versus 
with the
. Here 
is fixed
to be sufficiently small in order that each peak corresponds to a single energy eigen state. By the procedure (A) of finding several peaks in the narrow energy region, we can obtain the first evidence for the Higgs mode.
We suppose that the Higgs mode appears as a resonance on the infinitely large lattice. On the finite lattice,
Figure 1. The dynamical correlation of two spin operators 
with
. The lattice sizes are N = 20, 26, 32 and 36. We calculate them for the wave vector 
whose magnitude is non-zero and the smallest on each lattice.
this resonance consists of the several energy eigen states. We would like to investigate the resonance which survives in the large N limit. For this purpose we make several peaks in Figure 1 to merge to one broad peak by using the larger
. Therefore this 
must be larger than the energy difference between the peaks which form the resonance. On the other hand 
has to be smaller than the width of the resonance because, if we use the large
, the observed width becomes 
and irrelevant to the width of the Higgs mode.
By taking both conditions into account, we determine
. In following calculations we use this value. In Figure 2 of
, whose 
and the wave vector are the same as those in Figure 1 except for the value of
, we find the broad peaks. We can see that the cluster of peaks in Figure 1 merges to the single broad peak, which can be understood as the resonance. Such broad peak is found on all lattices. Although the energy at which we see the broad peak depends on the lattice size, this dependence is small.
Here we make a comment on the sharp peak whose energy
, which is isolated from the broad peak. As seen in Figure 1, this peak is given by a single energy eigen value. Therefore we conclude that this peak is irrelevant to the resonance. This conclusion is supported by vanishing of this peak in
, which will be shown in the next subsection.
3.2. Results for Total Spin S > 0
As discussed in the previous section, if the broad peaks found in Figure 2 are relevant to the Higgs mode, one should see similar peaks in the dynamical correlation of 
with other values of
. Figure 3 gives us the correlation on the N = 36 lattice with
. The clear broad peaks are found in 
for any
. Here note that the 
location, the height and the broadness of the peak change smoothly when 
increases.
In order to make quantitative discussion, we introduce definitions for the location of the peak and its broadness. First we find the 
where 
is maximal. Next we determine two values of
, at which
the value of 
is half of
. These two values are denoted as 
and 
. Here the central energy 
of a peak and the width 
are defined by
(19)
Figure 2. The dynamical correlation of two spin operators 
with
. The conditions are the same as those in Figure 1, except for the value of
.
Figure 3. The dynamical correlation of two spin operators 
with the wave vector 
on the lattice of N = 36. The values of 
are 0, 1, ∙∙∙, 6 and 7. In the figure 
is denoted by S.
(20)
For a concrete example, see Figure 4. Note that 
agrees with the resonance energy and 
agrees with its width, if 
is a simple form of the Breit-Wigner resonance.
In Figure 5 we plot 
and 
for 
on N = 26, 32 and 36 lattices. We find that 
depends on
, i.e. 
decreases with larger
. It seems that 
is the linear function of
. If we make the least square fit on each lattice, we obtain the errors of the fit, which are 0.058, 0.062 and 0.064 for N = 26, 32 and 36, respectively. These errors show that the linear function is acceptable for us. Also as dependences on the lattice size N, 
decreases weakly with larger N.
Figure 4. An example for the central energy 
and the width
. A black horizontal line denotes
. At
, whose location is expressed by the red dashed line, 
is maximal. The blue vertical lines show the locations of 
and
, where the horizontal dashed line is a half of the maximum value. The red solid line gives us
. The width 
is obtained by the energy distance between the blue dashed line and the red solid line.
Figure 5. The central energy 
(
) and the width 
(
) of the broad peaks in the dynamical correlation of two spin operators. 
and 
are defined by (19) and (20) in Subsection 3.2. Results are shown for the correlation on the lattices of the size N = 26, 32 and 36. Lines are obtained by making the least square fit.
Next we will discuss the width 
of the broad peak. 
is smaller with larger
, and approaches to
. If 
agrees with
, we understand that the peak is formed by a single eigen state. Also from this figure we observe that the width depend weakly on
. This dependence shows that we see the same resonance. By making the least square fit for
, we plot the fitted lines in the figure. The errors of the fit are 0.064, 0.054 and 0.087 for N = 26, 32 and 36, respectively. These errors are worse than those of
.
Summarizing this subsection we conclude that the observation in the state for 
is the second evidence for the Higgs mode, as discussed in the Section 2.
3.3. Two Kinds of the NG Modes
The SSB of the SU(2) symmetry of the Heisenberg antiferromagnet on the square lattice implies two kinds of the NG modes, as discussed in the previous section. One is the excited state of the small wave vector 
in
. Another is the excited state of the wave vector 
in
. From the discussion by the sigma model for the SSB, we have one Higgs mode which has the same interaction with any kind of the NG modes. Therefore in the dynamical correlation 
we should find the same resonance peak as that in 
for the small wave vector
. Since we calculate the correlation on the small lattice, the magnitude of the wave vector in our study is not so small. From the previous study [21] we can assume that the excited states with 
are candidates for the NG modes. On the N = 36 lattice, which is the maximal lattice in our calculation, the wave vector 
has the magnitude of 1.047, and the wave vector
has the magnitude of 1.481. Therefore on the N = 36 lattice we calculate the dynamical correlation on the excited states of the wave vectors 
and
, as well as 
and
. In addition this is calculated for the wave vectors of 
and 
on the N = 32 lattice. Here note that the wave vector 
has the magnitude of 1.111.
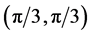
In Figure 6 we show 
with the above wave vectors. The first noticeable observation is the excellent agreement between peaks of the wave vector 
and
. On the peaks with the smallest wave vector 
and
, the agreement is not perfect due to the dip in the peak with
. As we will discuss in the summary, we suppose that the dip is artificial by the lattice symmetry. In order to confirm that this disagreement is accidental, we calculate 
with 
and the wave vector 
and
. These results are included in Figure 6, where we find the agreement between
Figure 6. The dynamical correlation of two spin operators 
with the wave vectors of 
and 
on the lattices N = 32 and 36. In the figure the expression of N = 36 is dropped. The results denoted by S =1 are the correlations with
, while other results are calculated with
. The expressions of k1, k2 and k3 show the wave vector
, 
, and
. T is used for
.
these peaks. Also the result on the N = 32 lattice shows the similar agreement between peaks of the correlation with the wave vector 
and
. These agreements can be explained by a fact that the Higgs mode couples to two kinds of the NG modes and it couples at the same strength to them. Therefore this observation is the strong evidence for the Higgs mode in the SU(2) symmetry.
3.4. Results about the XXZ Model
In this subsection we will carefully examine the broad peaks in 
and 
of the XXZ model.
As discussed in the previous subsection, the agreement between the peaks in these correlations reflects the symmetry of SU(2). If the symmetry of the model is U(1), we should not expect agreements between these peaks. Therefore we would like to study the correlation in the XXZ model which has only the U(1) symmetry. The Hamiltonian of the XXZ model is given by (15) in the Section 2. Since in this model the conserved charge is
, the 0-th component of conserved current corresponds with
. By this consideration, the NG mode appears in 
with the small wave vector 
and we can expect the broad peak by the Higgs mode in
. On the contrary the peak in 
is irrelevant to the Higgs mode.
In Figure 7 we show 
and 
about models of l = 0.1, 0.2, 0.3, 0.5, 0.8 and 1 (Heisenberg model). Here the lattice size N is 36 and the wave vector 
is
. As is expected, these peaks of 
and 
begin to separate from each other when l deceases from 1. The central energy 
of the broad peaks for the wave vector 
decreases when l deceases. Also the width 
becomes smaller. On the other hand the central energy 
for the wave vector 
increases and the width 
does not change clearly. We show the central energy of the broad peaks on the lattices of N = 26, 32 and 36 in Figure 8. From results in Figure 7 and Figure 8, we obtain the fourth evidence for the Higgs mode by the separated peaks in 
and 
in the XXZ model.
Figure 7. The dynamical correlation of two spin operators 
on the N = 36 lattice with the wave vectors 
and 
of the Heisenberg antiferromagnet and the XXZ models. The solid lines are results for
, whereas the dashed lines are for
. Also the value of l of the XXZ model is denoted by the value inside the expression XXZ(l).
Figure 8. The central energy 
of the broad peaks of the XXZ model for N = 26, 32 and 36. The symbol (
) is used for 
of the wave vector 
whose magnitude is the smallest on each lattice. Also we plot 
for 
by the symbol (
).
4. Summary and Discussion
In this work we have presented the numerical evidences for the Higgs mode of the spin-1/2 Heisenberg antiferromagnet on the square lattice, using the exact diagonalisation method and the finite temperature Lanczos method. Since the Higgs mode is the resonance which couples with the two Nambu-Goldstone (NG) modes, we calculate the dynamical correlation of the two spin operators with various wave vectors at zero temperature. For the dynamical correlation we have to calculate the inverse of the Hamiltonian operator. Since our calculations are carried out on the finite lattice, we need the smearing parameter 
to avoid the singular behavior of the inverse operator.
In this work we suggest four procedures (A)-(D) to find the Higgs mode in the calculation of the dynamical correlation. Using the first procedure (A) about peaks in the correlation with the small value of
, we observe many peaks in the narrow energy region, which gives us the first evidence for the Higgs mode. By calculations with the moderate value of
, we have found broad peaks on the lattices of various sizes. The second procedure (B) is suggested by a fact that the property of a state with any value of 
should agree with that of the state
, because the spontaneous breaking of the continuous symmetry requires the degenerated states. Although this agreement is obtained on the infinitely large lattice, the property on a state with non-zero value of 
on the finite lattice should be the smooth function of
. The study on the lattices of N = 26, 32 and 36 has shown that the central energy of the broad peaks is the linear function of
. This is the second evidence for the Higgs mode. By noticing that the SU(2) symmetry is broken by the O(3) scalar model, i.e. we have only one Higgs mode as well as two kinds of the NG modes, we suggest the third procedure (C). The Hamiltonian has the SU(2) symmetry so that we have the NG mode of the wave vector 
as well as those of 
for the small 
and
. Since these NG modes interact with the same Higgs mode, we should find the same broad peaks in the dynamical correlation with 
as those with
. The calculations of 
with 
and 
with 
on the lattice of N = 36 have given us the strong support for the same broad peaks. Also we find the same peaks in the calculations of 
with 
on the lattice of N = 32. These results give us the third evidence for the Higgs mode. By the observation of these same broad peaks, we suggest the fourth procedure (D), which makes a comparison between the Higgs modes of the SU(2) and the U(1) symmetry. For this purpose we study XXZ model which has only U(1) symmetry. In this model the excited mode of the wave vector 
for small 
and 
is the NG mode, while the mode of 
is not. Therefore the excited mode of the wave vector 
does not interact with the Higgs mode. Our study about the various XXZ models has showed that the broad peak in the correlation with 
is separated from the peaks with
. This observation has given us the fourth evidence. By these evidences we can confirm the existence of the Higgs mode in the Heisenberg antiferromagnet on the square lattice.
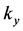
Now we comment on the dip that is seen in the broad peak of the correlation of N = 36, 
and
. The similar dip is found in the peak of N = 26, 
and
. We suppose that these dips are accidental because we do not see the dip for
. Also on the small lattices we do not see the dip, as shown in Figure 9. This figure gives us results of N = 18, 20, 25a and 25b for
, where the edge vectors are (3,3), (4,2), (4,3) and (5,0). Here we assume the symmetry of 
rotation. Also we can see the dependence of peaks on the edge vector, if we make a comparison between results of the edge vector (4,3) for 25a and that of the edge vector (5,0) for 25b.
Since we have calculated the central energy 
of the broad peak on many lattices, we discuss 
on the infinitely large lattice. When we assume that
(21)
we obtain 
for
, while we obtain 
for 
Although the estimated error is not small, one should note that this is clearly non-zero, and they give the same value. Using the same analysis for the width, we obtain 
for 
and 
for
. The width for 
does not agree with that for
, but it is clear that they are larger than
. This implies that we obtain the finite width on the infinitely large lattice.
Finally we would like to discuss about further study of the Higgs mode. If the broad peak is the resonance of the Higgs mode, we should find the same peak that has the same central energy 
and the same width 
for any pair of the NG modes of the wave vectors 
and
. In the present work we employ the exact diagonalisation approach, by which the size of the lattice is severely limited. As a result the wave vector is not small enough even for the N = 36 lattice, and we cannot find the same peak in the dynamical correlation with more than two kinds of the wave vectors. Therefore it is quite important to find the same peak for various wave vectors on larger lattices.
Figure 9. The dynamical correlation of two spin operators 
on the small lattices of N = 18, 20, 25a and 25b. The magnitude of the wave vector 
is the smallest for each lattice. The edge vector for N = 25a is (4,3), while it for N = 25b is (5,0). The lattice size is 25 for both edge vectors. The wave vectors for N = 18, 20, 25a and 25b are
, 
, 
and
, respectively.
In this work our calculations are made at the zero temperature. The extensive study at the finite temperature is an important subject because the experiments are performed at the finite temperature. Also the Higgs mode in two dimensional systems near a quantum critical point has been a subject of debate [15] - [20] . Our approach to the Higgs mode is useful to study models with the quantum phase transition.
Acknowledgements
M. T. thanks Dr. Yasuko Munehisa for every encouragement on his study.
Cite this paper
Tomo Munehisa, (2015) Numerical Study of the Higgs Mode in the Heisenberg Antiferromagnet on the Square Lattice. World Journal of Condensed Matter Physics,05,261-274. doi: 10.4236/wjcmp.2015.54027
References
- 1. Anderson, P.W. (1984) Basic Notions of Condensed Matter Physics. Benjamin/Cummings, Menlo Park.
- 2. Weinberg, S. (1995) The Quantum Theory of Fields. Vol. 2, Cambridge University Press, Cambridge.
http://dx.doi.org/10.1017/CBO9781139644167 - 3. Goldstone, J. (1961) Field Theories with Superconductor Solutions. Nuovo Cimento, 9, 154-164.
http://dx.doi.org/10.1007/BF02812722 - 4. Nambu, Y. (1960) Axial Vector Current Conservation in Weak Interactions. Physical Review Letters, 4, 380-382.
http://dx.doi.org/10.1103/PhysRevLett.4.380 - 5. Higgs, P.W. (1964) Broken Symmetries, Massive Particles and the Gauge Fields. Physics Letters, 12, 132-133.
http://dx.doi.org/10.1016/0031-9163(64)91136-9 - 6. Aad, G., et al. (2012) Observation of a New Particle in the Search for the Standard Model Higgs Boson with the ATLAS Detector at the LHC. Physics Letters B, 716, 1-29.
http://dx.doi.org/10.1016/j.physletb.2012.08.020 - 7. Charchyan, S., et al. (2012) Observation of a New Boson at a Mass of 125 GeV with the CMS Experiment at the LHC. Physics Letters B, 716, 30-61.
http://dx.doi.org/10.1016/j.physletb.2012.08.021 - 8. Hill, C.T. and Simmons, E. (2003) Strong Dynamics and Electroweak Symmetry Breaking. Physics Reports, 381, 235-402.
http://dx.doi.org/10.1016/S0370-1573(03)00140-6 - 9. Pekker, D. and Varma, C.M. (2015) Amplitude/Higgs Modes in Condensed Matter Physics. Annual Review of Condensed Matter Physics, 6, 269-297.
http://dx.doi.org/10.1146/annurev-conmatphys-031214-014350 - 10. Endres, M., Fukuhara, T., Pekker, D., Cheneau, M., Schaub, P., Gross, C. and Demler, E. (2012) The “Higgs” Amplitude Mode at the Two-Dimensional Superfluid/Mott Insulator Transition. Nature, 487, 454-459.
http://dx.doi.org/10.1038/nature11255 - 11. Ruegg, C., Normand, B., Matsumoto, M., Furrer, A., McMorrow, D.F., Kramer, K.W., Gudel, H.-U., Gvasaliya, S.N., Mutka, H. and Boehm, M. (2008) Quantum Magnets under Pressure: Controlling Elementary Excitations in TlCuCl3. Physical Review Letters, 100, Article ID: 205701.
http://dx.doi.org/10.1103/physrevlett.100.205701 - 12. Matsumoto, M., Normand, B., Rice, T.M. and Sigrist, M. (2004) Field- and Pressure-Induced Magnetic Quantum Phase Transitions in TlCuCl3. Physical Review B, 69, Article ID: 054423.
http://dx.doi.org/10.1103/PhysRevB.69.054423 - 13. Matsunaga, R., Hamada, Y., Makise, K., Uzawa, Y., Terai, H., Wang, Z. and Shimano, R. (2013) Higgs Amplitude Mode in the BCS Superconductors Nb1-xTixN Induced by Terahertz Pulse Excitation. Physical Review Letters, 111, Article ID: 057002.
http://dx.doi.org/10.1103/PhysRevLett.111.057002 - 14. Measson, M.-A., Gallais, Y., Cazayous, M., Clair, B., Rodiere, P., Cario, L. and Sacuto, A. (2014) Amplitude Higgs mode in the 2H-NbSe2 Superconductor. Physical Review B, 89, Article ID: 060503.
http://dx.doi.org/10.1103/PhysRevB.89.060503 - 15. Podolsky, D., Auerbach, A. and Arovas, D. (2011) Visibility of the Amplitude (Higgs) Mode in Condensed Matter. Physical Review B, 84, Article ID: 174522.
http://dx.doi.org/10.1103/physrevb.84.174522 - 16. Barlas, Y. and Varma, C.M. (2013) Amplitude or Higgs Modes in D-Wave Superconductors. Physical Review B, 87, Article ID: 054503.
http://dx.doi.org/10.1103/physrevb.87.054503 - 17. Tsuchiya, S., Ganesh, R. and Nikuni, T. (2013) Higgs Mode in a Superfluid of Dirac Fermions. Physical Review B, 88, Article ID: 014527.
http://dx.doi.org/10.1103/physrevb.88.014527 - 18. Gazit, S., Podolsky, D., Auerbach, A. and Arovas, D. (2013) Dynamics and Conductivity near Quantum Criticality. Physical Review B, 88, Article ID: 235108.
http://dx.doi.org/10.1103/physrevb.88.235108 - 19. Rancon, A. and Dupuis, N. (2014) Higgs Amplitude Mode in the Vicinity of a (2 + 1)-Dimensional Quantum Critical Point. Physical Review B, 89, Article ID: 180501.
http://dx.doi.org/10.1103/PhysRevB.89.180501 - 20. Gazit, S., Podolsky, D. and Auerbach, A. (2013) Fate of the Higgs Mode near Quantum Criticality. Physical Review Letters, 110, Article ID: 140401.
http://dx.doi.org/10.1103/physrevlett.110.140401 - 21. Richter, J., Schulenburg, J. and Honecker, A. (2004) Quantum Magnetism. In: Schollwock, U., Richter, J., Farnell, D.J.J. and Bishop, R.F., Eds., Lecture Note in Physics, Volume 645, Springer-Verlag, Berlin Heidelberg, 85-153.
- 22. Auerbach. A. (1994) Interacting Electrons and Quantum Magnetism. Springer-Verlag, Berlin Heidelberg.
http://dx.doi.org/10.1007/978-1-4612-0869-3 - 23. Hatano, N. and Suzuki, M. (1993) Quantum Monte Carlo Methods in Condensed Matter Physics. World Scientific, Singapore, 13-47.
- 24. De Raedt, H. and von der Linden, W. (1995) The Monte Carlo Method in Condensed Matter Physics. Springer-Verlag, Berlin Heidelberg, 249-284.
- 25. Munehisa, T. and Munehisa, Y. (2003) A New Approach to Stochastic State Selections in Quantum Spin Systems. Journal of the Physical Society of Japan, 72, 2759-2765.
http://dx.doi.org/10.1143/JPSJ.72.2759 - 26. Nishimori, H. and Nakanishi, H. (1988) Ground State of Quantum Spin Systems on the Triangular Lattice. Journal of the Physical Society of Japan, 57, 626-638. http://dx.doi.org/10.1143/JPSJ.57.626
- 27. Sandvik, A. and Hamer, C. (1999) Ground-State Parameters, Finite-Size Scaling, and Low-Temperature Properties of the Two-Dimensional S = 1/2 XY Model. Physical Review B, 60, 6588-6592.
http://dx.doi.org/10.1103/PhysRevB.60.6588 - 28. Jaklic, J. and Prelpvsek, P. (1994) Lanczos Method for the Calculation of Finite-Temperature Quantities in Correlated Systems. Physical Review B, 49, 5065-5068.
http://dx.doi.org/10.1103/PhysRevB.49.5065 - 29. Neuberger, H. and Zimman, T. (1989) Finite-Size Effects in Heisenberg Antiferromagnets. Physical Review B, 39, 2608-2618.
http://dx.doi.org/10.1103/PhysRevB.39.2608 - 30. Long, M.W., Prelovsek, P., El Shawish, S., Karadamoglou, J. and Zotos, X. (2003) Finite-Temperature Dynamical Correlation Using the Microcanonical Ensemble and the Lanczos Algorithm. Physical Review B, 68, Article ID: 235106.
http://dx.doi.org/10.1103/physrevb.68.235106 - 31. Jaklic, J. and Prelpvsek, P. (2000) Finite-Temperature Properties of Doped Antiferromagnets. Advance Physics, 49, 1- 92.
http://dx.doi.org/10.1080/000187300243381 - 32. Munehisa, T. (2014) An Improved Finite Temperature Lanczos Method and Its Application to the Spin-1/2 Heisenberg Model on the Kagome Lattice. World Journal of Condensed Matter Physics, 4, 134-140.
http://dx.doi.org/10.4236/wjcmp.2014.43018