World Journal of Condensed Matter Physics
Vol.05 No.03(2015), Article ID:58444,10 pages
10.4236/wjcmp.2015.53014
Transport Characteristics of Charge Carriers in Normal State Superconductor YBa2Cu3O7−d
Vilius Palenskis
Physics Faculty, Vilnius University, Vilnius, Lithuania
Email: vilius.palenskis@ff.vu.lt
Copyright © 2015 by author and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 27 May 2015; accepted 27 July 2015; published 30 July 2015
ABSTRACT
The general expressions based on the Fermi distribution of the free charge carriers are applied for estimation of the transport characteristics in superconductors at the temperature well above the superconducting phase transition temperature TC. The Hall-effect experimental results in the normal state of the superconductor YBa2Cu3O7−d are not finally explained. On the ground of the randomly moving charge carriers, the transport characteristics of the randomly moving charge carriers for both single type and two types of the charge carriers are presented. The particular attention has been pointed to the Hall-effect measurement results of the high-TC superconductor YBa2Cu3O7−d. It is at the first time derived the Hall coefficient expression for two type of highly degenerate charge carriers (electrons and holes) on the ground of the randomly moving charge carriers at the Fermi surface. It is shown that the Hall coefficient and other transport characteristics are determined by the ratio between the electron-like and hole-like densities of states at the Fermi surface.
Keywords:
Randomly Moving Charge Carrier Density, Electrical Conductivity, Two-Band Model, Hall Coefficient, Hall Mobility, Drift Mobility, Density of States

1. Introduction
In all cuprates whose doping has been optimized for maximum superconducting transition temperature TC, the resistivity
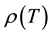 well above TC is quite accurately linear in T as for ordinary metals. So, the resistivity is proportional to
well above TC is quite accurately linear in T as for ordinary metals. So, the resistivity is proportional to
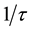 (here t is the average electron scattering time). In metal the Hall coefficient is independent on temperature which is considered that mobile carrier density is constant and equal to the valence electron density. As it is presented in [1] -[3] , the conductivity is determined by the effective density of randomly moving charge carriers neff. For metals, normal state superconductors and other materials with degenerate electron gas the effective density of randomly moving charge carriers is determined by the density of states
(here t is the average electron scattering time). In metal the Hall coefficient is independent on temperature which is considered that mobile carrier density is constant and equal to the valence electron density. As it is presented in [1] -[3] , the conductivity is determined by the effective density of randomly moving charge carriers neff. For metals, normal state superconductors and other materials with degenerate electron gas the effective density of randomly moving charge carriers is determined by the density of states
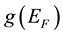 at the Fermi energy EF:
at the Fermi energy EF:
 (here k is the Boltzmann constant, and T is the absolute temperature). The density of states
(here k is the Boltzmann constant, and T is the absolute temperature). The density of states
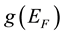 is obtained from the experimental results of the electron heat capacity measurements. For multivalent metals and superconductors in the normal state with the composite density of states, the Hall coefficient does determine neither the total density of free electrons, nor the effective density of randomly moving charge carriers.
is obtained from the experimental results of the electron heat capacity measurements. For multivalent metals and superconductors in the normal state with the composite density of states, the Hall coefficient does determine neither the total density of free electrons, nor the effective density of randomly moving charge carriers.
How to understand the temperature dependences of both resistivity
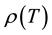 and Hall coefficient
and Hall coefficient
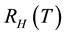 of YBa2Cu3O7 (YBCO) in terms of a unified physical picture is still an open question. In almost all works the explanation of the resistivity
of YBa2Cu3O7 (YBCO) in terms of a unified physical picture is still an open question. In almost all works the explanation of the resistivity
 in ab plane is based upon a 2D single-band model for holes. The nearly linear T dependence of
in ab plane is based upon a 2D single-band model for holes. The nearly linear T dependence of
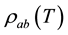 is obtained by assuming the free density of charge carriers to be constant and deducing the approximate relation
is obtained by assuming the free density of charge carriers to be constant and deducing the approximate relation
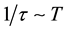 from electron-phonon interaction. In YBCO there is also an appreciable anisotropy of conductivity within ab plane, as one will expect because of the mobile holes on the chains. For YBCO optimized for maximum TC the resistivity
from electron-phonon interaction. In YBCO there is also an appreciable anisotropy of conductivity within ab plane, as one will expect because of the mobile holes on the chains. For YBCO optimized for maximum TC the resistivity
 in a direction is about double of
in a direction is about double of
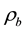 in b direction, and they have the same temperature dependences [4] . The ratio
in b direction, and they have the same temperature dependences [4] . The ratio
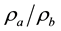 value is about 2.2 and is independent on temperature; it indicates that the Cu-O chains contribute about 60% of the current when the electric field is parallel to them, with the rest of the current being contributed by the Cu-O planes. The electrical resistivity in the c direction is high, as it is expected from the localization in the c direction of the most electron states in the planes. It is believed that they are tunneling from one layer to the next in the c direction [5] . On the other hand, the measurement of the Hall coefficient for a single-crystal YBCO shows that for magnetic field parallel to c axis and for the direct current in ab plane RH is proportional to 1/T, and the charge carriers are holes with
value is about 2.2 and is independent on temperature; it indicates that the Cu-O chains contribute about 60% of the current when the electric field is parallel to them, with the rest of the current being contributed by the Cu-O planes. The electrical resistivity in the c direction is high, as it is expected from the localization in the c direction of the most electron states in the planes. It is believed that they are tunneling from one layer to the next in the c direction [5] . On the other hand, the measurement of the Hall coefficient for a single-crystal YBCO shows that for magnetic field parallel to c axis and for the direct current in ab plane RH is proportional to 1/T, and the charge carriers are holes with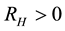 .
.
A study is usually starting from a single parabolic band picture, but there is a problem on explanation of temperature dependences of both conductivity and Hall coefficient: the former implying that
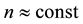 with
with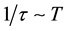 , and another implying that
, and another implying that


and

are not longer hold. As it is shown in [1] -[3] , these formulas are valid neither for usual metals, nor for materials with degenerate electron gas, because the electrons with the energy well below the Fermi level can’t change their energy E either through scattering or due to external fields as all these states are occupied; the Fermi distribution function leads to
2. The Basic Transport Characteristics for Degenerate Materials with One Type of Randomly Moving Charge Carriers
The effective density of randomly moving electrons neff can be presented as [1] -[3]

This relation is valid in all cases. In the case of high degree of degeneracy, the effective density of randomly moving electrons can be expressed as

where geff(EF) is the total density of states at
For degenerate materials with one type of randomly moving charge carriers such general expressions can be presented [2] [3] :
for conductivity:

for drift mobility (Figure 1):

for Hall mobility (Figure 2):

for Hall coefficient:

for plasma frequency:
Figure 1. Drift mobility (absolute value) for single type of charge carrier dependence on temperature in YBa2Cu3O7 (calculation quantities are taken from Table 1).
Figure 2. Hall mobility (absolute value) for single type of charge carrier dependence on temperature in YBa2Cu3O7 (calculation quantities are taken from Table 1).
Table 1. Charge carrier transport parameters of superconductor YBa2Cu3O7 in the normal state.
Note: The mark * note that the same absolute values are for the randomly moving electrons and holes.

where






As shown in [6] [7] , the average electron scattering time at the Fermi surface at linear resistivity dependence on temperature T range in highly degenerate materials is equal:

where


So, the drift mobility in highly degenerate materials can be ten or hundred times larger than Hall mobility. Equation (9) shows that plasma frequency for highly degenerate materials directly does not depend on the effective mass of charge carriers.
On the ground of both the resistivity r [8] and the electron heat capacity coefficient γ [9] measurement results for high quality superconductor YBa2Cu3O7 in Table 1 there are presented its charge carrier transport parameters in the normal state evaluated on the base of randomly moving charge carrier theory (near each parameter there are cited the equation according to which the mentioned value was calculated). There also has been considered that quasiparticles electrons and holes randomly are moving independently.
It is worth here to point that the randomly moving charge carrier density neff in high degenerate materials is not constant, but is proportional to temperature T. At linear resistivity dependence on temperature range


3. The Basic Transport Characteristics for Degenerate Materials with Two Type of Randomly Moving Charge Carriers and Its Applications to Superconductor YBa2Cu3O7−d
It is pointed out that the electron-phonon scattering, not the phonon-assisted electron hopping, is highly likely responsible for in ab plane transport of the high-TC YBCO [8] . It is considered that the linear T dependence of the in-plane resistivity


The ab plane Hall coefficient of YBa2Cu3O7−d has the following characteristics [10] -[12] : a) the sign of the Hall coefficient RH is positive, i.e. hole-like; b) RH is very sensitive to the oxygen content and increases rapidly with increasing oxygen deficiency d; c) RH is strongly temperature dependent, that means this is a multiband system; for a well oxygenate samples (TC is over 90 K) the temperature dependence is such that the quantity




Usually in literature using a two-band model, the conductivity and the Hall coefficient are expressed in terms of the densities of both electrons ne and holes nh and their mobilities me and mh [11] [13] -[16] :
Figure 3. Illustration of density of states







In these relations on the ground that the average scattering time is defined by scattering time on the Fermi surface:



with
In [8] , it is proposed that the key quantity is not RH, but the Hall angle which at weak magnetic field


Thus, the relaxation time tH which determines



As it was mentioned earlier, Equation (13) was derived on the misconstruction base that drift and Hall mobilities for degenerate materials coincide. Let us define the Hall coefficient on the ground of the effective density of randomly moving charge carriers for two types of charge carriers: holes and electrons. The general expressions for conductivity and Hall coefficient can be presented as [18] [19] :


There the relation



In degenerate materials the effective densities of randomly moving charge carriers and their absolute values of drift and Hall mobilities can be presented in the following way [1] -[3] :




where ge(EF) and gh(EF) are electron-like and hole-like effective densities of states at the Fermi surface, respectively; vF and tF are the velocity and the average scattering time of charge carriers at the Fermi surface, respectively. Accounting Equations (21)-(24), Equations (19) and (20) can be presented in such a form:


or in simplified form (by using Equation (8)):

where




Thus, one can present Equation (27) in such simplified form:

where

The quantity η plays the role of compensation of voltages caused by holes and electrons in Hall effect measurement in degenerate material, and the quantity


It was interesting to find such electron-like and hole-like densities of states dependences on temperature in such a way that they could cause the Hall coefficient RH2 proportionality to



From Equations (7), (18) and (28) the effective expression of Hall mobility for two types of randomly moving charge carriers (holes and electrons) can be presented in the following form:

where


In the case of randomly moving electron and hole quasiparticles, the expressions for Hall coefficient (Equation (28)) and for Hall mobility (Equation (30)), and considering that conductivity dependence on temperature
Figure 4. The hole-like and electron-like densities of states dependence on temperature for superconductor YBa2Cu3O7−d, which cause the Hall coefficient RH2 ~ 1/T.
Figure 5. The compensation degree factor dependence on temperature for superconductor YBa2Cu3O7−d.
Figure 6. Hall coefficient 1/RH2 dependence on temperature in the normal state temperature range for YBa2Cu3O7−d.
Figure 7. The Hall mobility mH2 value dependence on temperature for randomly moving holes and electrons in YBa2Cu3O7−d with the densities of states presented in Figure 4.
are only due to


As pointed in [5] , that near optimum doping rising the temperature has a similar effect, possibly by releasing carriers from localized states or by increasing the effective hole doping in the CuO2 layers, or by changing the effective band structure, i.e. changing the effective density of electron-like and hole-like states. In [21] , it is pointed that due to displacement of oxygen atoms in chains there can be changes of density of states in-plane and in chain states.
So, when the hole-like and electron-like densities of states are close to one other then the small changes of these densities with temperature can produce the drastic changes in temperature dependence of Hall coefficient RH2 and Hall mobility mH2 in the case of two types of charge carriers: electrons and holes.
4. Conclusion
This work tries to attract attention to interpretation of transport properties of superconductor YBa2Cu3O7−d in temperature range well over the transition temperature TC. On the base of the density of randomly moving charge carriers and their drift and Hall mobilities, the general expressions for Hall coefficient and Hall mobility for two types of charge carriers―holes and electrons were derived. Considering that Hall coefficient RH1 for degenerate material with single type of charge carriers is completely defined, from the measurement of Hall coefficient RH2 in degenerate material with electrons and holes it possible to determine the compensation degree factor 1/η, and the part of electron-like and hole-like densities of states at the Fermi surface, and they changes with temperature. When the hole-like and electron-like densities of states are close to other ones, the small changes of these densities with temperature can produce the drastic changes in temperature of Hall coefficient RH2 and Hall mobility mH2. It is shown that scattering time tF always has its usual dependence on temperature: tF ~ 1/T.
Acknowledgements
This study was partially funded by European Social Fund under Global Grant measure No. VP1-3.1-ŠMM-07- 03-040.
Cite this paper
ViliusPalenskis, (2015) Transport Characteristics of Charge Carriers in Normal State Superconductor YBa2Cu3O7-δ. World Journal of Condensed Matter Physics,05,118-128. doi: 10.4236/wjcmp.2015.53014
References
- 1. Palenskis, V. (2013) Drift Mobility, Diffusion Coefficient of Randomly Moving Charge Carriers in Metals and Other Materials with Degenerate Electron Gas. World Journal of Condensed. Matter Physics, 3, 73-81. http://dx.doi:104236/wjcmp.2013.31013
- 2. Palenskis, V. (2014) The Effective Density of Randomly Moving Electrons and Related Characteristics of Materials with Degenerate Electron Gas. AIP Advances, 4, 047119-1(9).
http://dx.doi.org/10.1063/1.4871757 - 3. Palenskis, V. (2013) A Novel View to Free Electron Theory. Materials with Degenerate Electron Gas. LAP LAMBERT Academic Publishing, Saarbrücken.
- 4. Friedman, T.A., Rabin, M.W., Giapintzakis, J., Rice, J.P. and Ginsberg, D.M. (1990) Direct Measurement of the Anisotropy of the Resistivity in the a-b Plane of Twin-Free, Single-Crystal, Superconducting YBa2Cu3O7-δ. Physical Review B, 42, 6217-6221. http://dx.doi.org/10.1103/PhysRevB.42.6217
- 5. Waldram, J.R. (1996) Superconductivity of Metals and Cuprates, Chapter 14: Normal-State Transport Properties in the Cuprates. Institute of Physics Publishing, Ltd., London.
- 6. Devillers, M.A.C. (1984) Lifetime of Electrons in Metals at Room Temperature. Solid State Communications, 49, 1019-1022. http://dx.doi.org/10.1016/0038-1098(84)90413-7
- 7. Lemberger, T.R. and Coffey, L. (1988) Effects of Inelastic Electron Scattering on Properties of High-Temperature Superconductors. Physical Review B, 38, 7058-7060.
http://dx.doi.org/10.1103/PhysRevB.38.7058 - 8. Andersen, P.W. (1997) The Theory of Superconductivity in the High-TC Cuprates. Chapter 3. Normal State Properties in the High-TC Superconductors: Evidence for Non-Fermi Liquid States. Princeton Series in Physics, Princeton University Press, Princeton.
- 9. Volovik, G.E. (1989) Nonzero State Density in Superconductors with High Transition Temperature. Journal of Experimental and Theoretical Physics Letters, 49, 790-792.
- 10. Xing, D.Y., Liu, M. and Ting, C.S. (1988) Out-off-Plane Transport Mechanism in the High-TC Oxide Y-Ba-Cu-O. Physical Review B, 38, 11992-11995. http://dx.doi.org/10.1103/PhysRevB.38.11992
- 11. Dresselhaus, M.S. (2001) Solid State Physics, Part IV: Superconducting Properties of Solids. 6.732, Fall.
- 12. Lu, Y., Zhao, B.R., Yuan, C.W., Zhang, Y.Z., Wang, H.S., Shi, Y.H., Xu, P. and Li, L. (1989) The Hall Coefficient of YBa2Cu3O7-x Thin Films with (100) Orientation. Zeitschrift für Physik B Condensed Matter, 74, 283-287. http://dx.doi.org/10.1007/BF01307874
- 13. Eagles, D.M. (1989) Concentrations and Mobilities of Holes and Electrons in a Crystal of a 90K Oxide Superconductor from Analysis of ab-Plane Resistivity and Hall Data. Solid State Communications, 69, 229-234. http://dx.doi.org/10.1016/0038-1098(89)90840-5
- 14. Xing, D.Y., Liu, M. and Ting, C.S. (1988) Out-off-Plane Transport Mechanism in the High-TC Oxide Y-Ba-Cu-O. Physical Review B, 38, 11992-11995. http://dx.doi.org/10.1103/PhysRevB.38.11992
- 15. Xing, D.Y. and Ting, C.S. (1988) Two-Band Model for Anisotropic Hall Effect in High-TC Y-Ba-Cu-O. Physical Review B, 38, 5134-5137. http://dx.doi.org/10.1103/PhysRevB.38.5134
- 16. Ginsberg, D.M. (Ed.) (1992) Physical Properties of High Temperature Superconductors. World Scientific Publishing Co., Singapure.
- 17. Hikita, M. and Suzuki, M. (1989) Magnetoresistance and Thermodynamic Fluctuations in Single-Crystal YBa2Cu3Oy. Physical Review B, 39, 4756-4759. http://dx.doi.org/10.1103/PhysRevB.39.4756
- 18. Ziman, J.M. (1972) Principles of the Theory of Solids. Cambridge University Press, Cambridge.
http://dx.doi.org/10.1017/CBO9781139644075 - 19. Markiewicz, R.S. (1988) Simple Model for the Hall Effect in YBa2Cu3O7-δ. Physical Review B, 38, 5010-5011. http://dx.doi.org/10.1103/PhysRevB.38.5010
- 20. Foro, L., Raki, M., Henry, J.Y. and Ayache, C. (1989) Hall Effect and Thermoelectric Power of an YBa2Cu3O6.8 Single Crystal. Solid State Communications, 69, 1097-1101.
http://dx.doi.org/10.1016/0038-1098(89)90493-6 - 21. Anisimov, V.I., Korotin, M.A. and Afanasyev, I.V. (1988) Influence of Displacement of Chain Oxygen Atoms on the Electronic Structure of YBa2Cu3Oy. The Physics of Metals and Metallography, 66, 161-193.









