Received 20 August 2014; revised 21 September 2014; accepted 2 October 2014

ABSTRACT

The ground-state energy and its derivate of the acoustic polaron in free-standing slab are calculated by using the Huybrechts-like variational approach. The criteria for presence of the self- trapping transition of the acoustic polaron in free-standing slabs are determined qualitatively. The critical coupling constant for the discontinuous transition from a quasi-free state to a trapped state of the acoustic polaron in free-standing slabs tends to shift toward the weaker electron- phonon coupling with the increasing cutoff wave-vector. Detailed numerical results confirm that the self-trapping transition of holes is expected to occur in the free-standing slabs of wide-band- gap semi-conductors.

Keywords:

free-standing slabs, acoustic polaron, self-trapping

1. Introduction

The electron mobility is important because it is a parameter which associates microscopic electron motion with macroscopic phenomena such as current-voltage characteristics. The mobility will be changed markedly if electron state transforms from the quasi-free to the self-trapped. Moreover, many physical properties of photoelectric material are also influenced by the electron state. The self-trapping of an electron is due to its interaction with acoustic phonons. The polaron problem had also gained interest in explaining the high- superconductors and describing the impurities of lithium atoms in Bose-Einstein ultracold quantum gases condensate of sodium atoms. Therefore the problems of acoustic polaron had been maintained interest of many scientists in the past decades [1] -[17] .

Various calculations for the ground-state energy of the acoustic polaron as a function of the e-p coupling strength have led to a discontinuous transition from a quasi-free state to a trapped state [4] - [10] . One had known that the e-p coupling effects will be substantially enhanced in confined structure, such as quasi two-dimensional (Q2D) system, so that the self-trapping transition would be easier to realize. It is meaningful to judge the possibility of the self-trapping of electron in free-standing slab systems.

It is determined in our previous works [8] that the self-trapping of the electrons in AlN as well as the holes in AlN and GaN is expected to be observed in 2D system. As a Q2D structure, the slab can be realized for most of the wide-band-gap semiconductors. Therefore the criterion for the presence of the self-trapping of electron in free-standing slab systems is desired.

In this work, a new Hamiltonian describing the deformation potential interaction between the electron and the acoustic phonon in free-standing slab systems will be derived. The self-trapping transition of the Q2D acoustic polaron will be discussed.

2. The e-LA-p Interaction Hamitonian

The interaction between the electron and the longitudinal acoustic phonon (e-LA-p) in free-standing slab is given by [13]

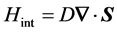(1)

where is the deformation potential constant, and 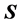is the displacement vector of the acoustic phonon.

In the free-standing slab, the displacements can be taken as the form:

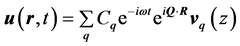(2)

where 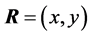and are in-plane position and phonon wave vectors, respectively, , 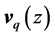represents the 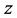-dependence of the normal mode, and 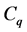is a constant. 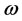is the phonon frequency. For mixed pressure shear vertical (MPSV) modes 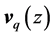can be written as [13]

(3)

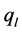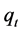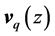
where and are z-components of the longitudinal and transverse phonon wave vectors. Here the constant are arbitrary as long as the does not diverge at, and the and satisfy the following relation:

(4)

The at interface of the slab must satisfy normalization integral

(5)

Inserting Equations (3) and (4) into (5), one can obtain the following relation

(6)

where, are Lame constants, is the mass density of the slab crystal, is the thickness of free- standing slab.

Inserting Equations (6), (3) and (2) into (1), the e-LA-p coupling Hamiltonian is then written as

(7)

Here the e-p coupling function has the following form:

(8)

Then the e-LA-p system Hamiltonian in the free-standing slab is written as

(9)

where denotes the kinetic energy of the electron. The acoustic phonon contribution is given by

.

3. The Ground-State Energy

In this section, a Huybrechts-like variational approach [18] is to be used to calculate the ground-state energy of the acoustic polaron in free-standing slab.

Firstly we carry out a unitary transformation

(10)

where a is a variational parameter and will tend to 0 in the strong coupling limit and 1 in the weak coupling limit. Therefore, the Hamiltonian turns into

(11)

Then let us introduce the linear combination operators of the position and momentum of the electron by the following relations

(12a)

And

(12b)

where and are respectively the creation and annihilation operator and. is another variational parameter.

Inserting (12a) and (12b) into (11) and performing the second unitary transformation

(13)

The Hamiltonian finally becomes the following form:

(14)

Here we have omitted the multi-phonon processes, which contribute less to the polaronic energy.

The displacement amplitude in the second unitary transformation is determined as

(15)

by the diagonalization of the vital important part of.

The ground-state energy can be calculated by averaging Hamiltonian (14) over the zero-phonon state of the acoustic polaron, for which we have

(16)

By some standard treatments, the variational energy of the polaronic ground-state can be obtained as follows

(17)

The e-LA-p coupling constant is given by

(18)

In Equation (18) the variational parameters and will be determined by numerically minimizing the energy in the following section.

4. Results and discussions

The variational calculations for the ground-state energies of the acoustic polaron in free-standing slabs are numerically performed for different thickness of the slab and cutoff wave vector, by using Equation (17). To compare with the previous results [6] [8] [9] , we have also expressed the energy in units of and the phonon vector in units of in the calculations.

As can be seen in Figure 1(a), in case of the thickness of the slab is 0.1 and the cutoff wave vector is 30, the ground-state energy appears a knee with respect to at, where the derivative of the ground-state energy has a discontinuous point, which is called “phase transition” critical point, where the polar on state transforms from the quasi-free to the self-trapped. When and 120, the critical points are at and 0.0061, respectively, where one can find knees in the ground-state energies, and discontinuous points in the derivatives with respect to in Figure 1(b) and Figure 1(c). It is obviously that the critical point shifts toward the weaker e-p coupling with the increasing cutoff wave-vector. Figure 2 exhibits the results of ground-state energies and derivatives of the acoustic polarons in free-standing slabs for. One can find in Figure 2 that the critical coupling constants are around 0.060, 0.031 and 0.014, for, 60 and 120, respectively. It is also found that the position of the critical point is sensitive to the cutoff wave-vector and shifts also toward the direction of smaller e-p coupling with the increasing cutoff wave-vector. The character of the critical coupling constant varying with the cutoff wave-vector is consistent with the previous papers [6] [7] [9] .

It is worth noting the critical values of the e-p coupling constant increase with the increasing thickness of the slab. For example, when the cutoff wave-vector equals to 60, the critical coupling constant, , is around 0.0124 for the radius is 0.1 (Figure 1), where as, when the radius is 20 (Figure 2). Which we thought the e-p coupling strength weakened with the increasing thickness of slab.

The had been used as a criterion for the self-trapping transition qualitatively. It is obviously that the for different values of cutoff wave-vectors almost tend to a given value of 0.75, when the thickness of slab is 0.1. Similarly result had also been obtained in the slabs with radius of 20. The products of are all close to 1.8. Therefore, can also be used as a qualitative criterion for the presence of the self-trapping transition of the acoustic polaron in slabs. Acoustic polaron in free-standing slab systems can be self-trapped if is larger than the.

Now we use the criterion of the to judge the possibility of self-trapping transition for the acoustic polaron in real free-standing slab materials. First we consider the semiconductors of GaN and AlN. In our previous work, it was indicated that the holes in GaN and both the electrons and holes in AlN are expected to have the self-trapping transition in 2D systems [8] . In present work, even (0.24 for GaN and 0.57 for AlN) can get the same order of magnitude as (0.75), the self-trapping transition is still difficult to be observed. Which we thought the e-p coupling strength in slab is weaker than that in 2D system for the weakening of confined dimension in the vertical plane direction.

Holes have larger effective masses than electrons and must be easier to be self-trapped. For GaN, which has the light and heavy-hole masses 0.37 and 0.39 [8] respectively, the corresponding product and 1.01 are both large enough to have self-trapping transition in slab systems for the thickness is 0.1. Similarly the light-hole mass in AlN is 0.47 [8] and the product is smaller than the critical value in 3D system

but larger than that in slab. Therefore the light-hole in AlN can be self-trapped only in the slab with. However the heavy-hole mass in AlN is 0.73 [8] and the product is sufficiently lager to have self-trapping in the slab with sufficient thickness of 20.

5. Summary

The critical coupling constant for the self-trapping transition of the acoustic polarons in free-standing slab systems is determined by calculating the ground-state energies and the derivates of the acoustic polaron. The value of the criterion of the acoustic polaron in slab systems is smaller than that in 3D system. Nevertheless, the value for slab is over that in 2D system [8] . Therefore, the self-trapping transition of the acoustic polaron in slab is a little more difficult to be realized than that in 2D system. It is still worth someone’s attentions, for which the transition of the acoustic polaron in slab is easier to be realized than that in 3D system.

Acknowledgements

This work is supported under Grant No. 11147159 from the National Natural Science Foundation of China.

References