World Journal of Condensed Matter Physics
Vol.4 No.3(2014), Article
ID:48804,6
pages
DOI:10.4236/wjcmp.2014.43015
The Coexistence of Super Conductivity and Spin Density Wave (SDW) in SmO1−xFxFeAs
Dagne Atnafu, Poran Singh
Department of Physics, Addis Ababa University, Addis Ababa, Ethiopia
Email: dagneatnafu2@yahoo.com, psinghgbpub@yahoo.com
Copyright © 2014 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 22 April 2014; revised 1 June 2014; accepted 28 June 2014
ABSTRACT
The coexistence of superconductivity and spin density wave in SmO1−xFxFeAs is theoretically studied using the model Hamiltonian which contains BCS type superconductivity and spin density wave terms. Employing green function formalism, the expression for the spin density wave order parameter (M) and expression for spin density wave transition temperature TSDW is obtained. The interplay between the superconductivity and spin density wave is examined in these parameters and the coexistence of the two states is established in the order parameter range of 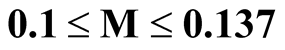 meV which is seen to be in broad experimental agreement.
meV which is seen to be in broad experimental agreement.
Keywords:Coexistence, Superconducting Order Parameter, Spin Density Wave Order Parameter and Green Function

1. Introduction
The discovery superconductivity with a transition temperature of 26 K in LaO1−xFxFeAs system [1] has generated tremendous interest in the scientific community. Shortly after this discovery, several groups reported an increase of Tc values by replacing La with smaller-size rare-earth ions (Tc = 41 K in CeO1−xFxFeAs [2] , Tc = 52 K in NdO1−xFxFeAs [3] , Tc = 52 K in PrO1−xFxFeAs [4] [5] and the substitution of La with Sm, Tc was found to be 55 K in SmO1−xFxFeAs [6] [7] .
Besides a relative high Tc, the system displays many interesting properties. First, they promise interesting physics that stem from the coexistence of superconductivity and magnetism. Second, they provide a much wider variety of compounds for research and, with their multi-band electronic structure; they offer the hope of finally discovering the mechanism of high temperature superconductivity and finding the way to increase Tc [8] .
The parent compounds of these materials are itinerant spin density wave magnetic order or anti ferromagnetic order [9] [10] . Superconductivity emerges when doping a magnetic mother compound with electron or holes and thereby suppressing the magnetic order [9] [11] . The proximity of the superconductivity state to the spin density wave phase in the phase diagram implies that the interplay between the magnetism and superconductivity might play an important role in understanding the pairing mechanism and other physical properties of the iron-based superconductors. It is generally believed that the magnetic couplings between the itinerant electrons and/or between the itinerant electron and local spin are essential to both spin density wave instability and superconductivity.
The Muon spin rotation study on the newly discovered iron pnictide superconductor found that magnetism and superconductivity coexist in the long rang doping in SmO1−xFxFeAs (0.1 ≤ x ≤ 0.13) [12] .
In the present work we study theoretical coexistence of superconductivity and spin density wave in SmO1−xFxFeAs. The model of the Hamiltonian used in describing the system incorporate two competing physical processes involving the electron hole like pairing and electron-electron pairing. The results of our work clearly show that over certain order parameter range superconductivity and spin density wave are established.
2. Formulation of the Problem
The model of the Hamiltonian for coexistence spin density wave and superconductivity in our compound can be describe as
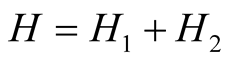 (1)
(1)
where , the first term of
, the first term of 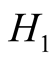 represent single particle energies of the conduction and the second term BCS type electron-electron pairing;
represent single particle energies of the conduction and the second term BCS type electron-electron pairing;  is spin density wave Hamiltonian term;
is spin density wave Hamiltonian term; 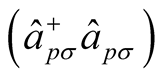 are the creation (annihilation) operators of an electron having the wave number
are the creation (annihilation) operators of an electron having the wave number 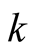 and spin
and spin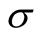 .
.
 is superconducting order parameter;
is superconducting order parameter; 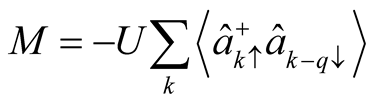 is the spin density wave order parameters.
is the spin density wave order parameters.
The double-time temperature dependent retarded Green function is given by (Zubarev) [13]
 (2)
(2)
where  is abbreviated notation for the corresponding the Green’s function and
is abbreviated notation for the corresponding the Green’s function and  indicates the average over a grand canonical ensemble for the operators.
indicates the average over a grand canonical ensemble for the operators.  is Heaviside step function,
is Heaviside step function, 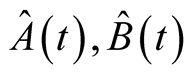 are operators in Heisenberg picture.
are operators in Heisenberg picture.
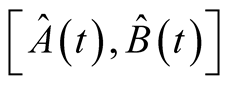 is a commutator or anticommutator.
is a commutator or anticommutator.
To find the equation of motion for the Green’s function, differentiating equation (2) with respect to time and, we get
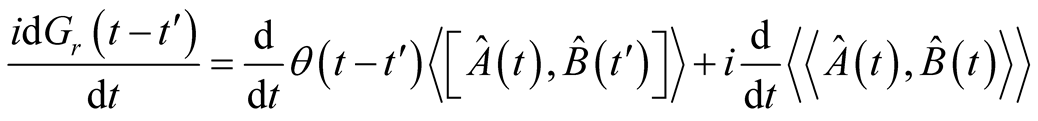 (3)
(3)
The relation between Heaviside step function 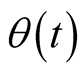 and Dirac delta function δ is given by
and Dirac delta function δ is given by
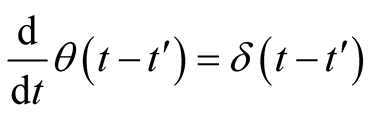 (4)
(4)
The equation of motion expresses as,
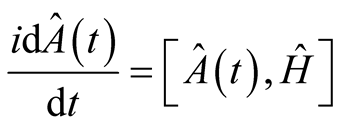 (5)
(5)
Based on the relation between Heaviside step function  and Dirac delta function
and Dirac delta function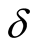 , equation (3) can be written as
, equation (3) can be written as
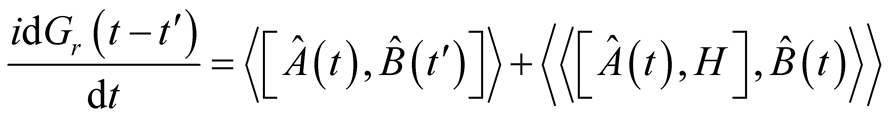 (6)
(6)
The Fourier transformation of 
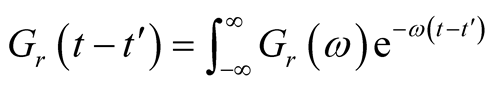 (7)
(7)
Considering delta function, the derivative of equation (7) become
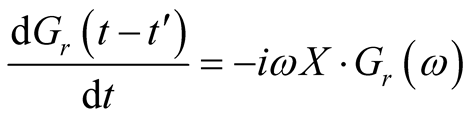 (8)
(8)
Comparing equation (6) and (8), we get
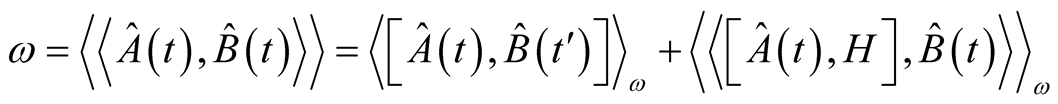 (9)
(9)
2.1. Dependence of SDW (M) on the Superconductivity Critical Temperature (Tc)
The equation of motion for the correlation  can be written as;
can be written as;
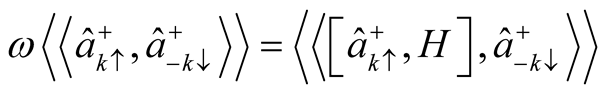 (10)
(10)
Solving the commentator in equation (10), we get
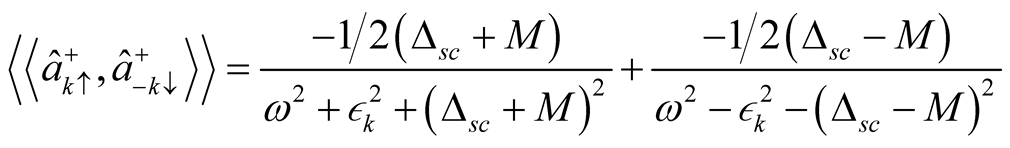 (11)
(11)
Using the expression  and Matsubara’s frequency, we have
and Matsubara’s frequency, we have
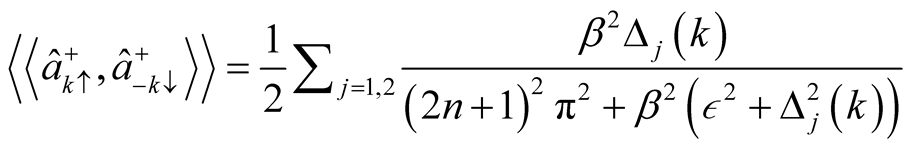 (12)
(12)
Thus, the superconductivity order parameter 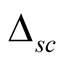 can be expressed as follows
can be expressed as follows
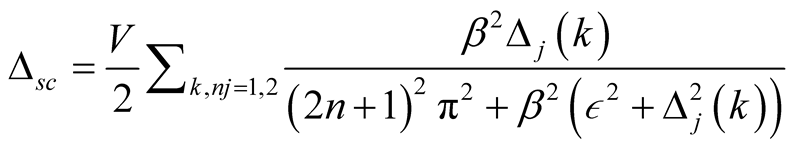 (13)
(13)
Let us employ the following equality relation below to solve the superconductivity order parameter
 (14)
(14)
Using the above equality relation, the superconducting order parameter can be expressed as
 (15)
(15)
Converting the summation over 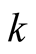 values into an integral by introducing the density of state
values into an integral by introducing the density of state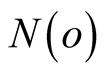 , we can write superconducting order parameter as
, we can write superconducting order parameter as
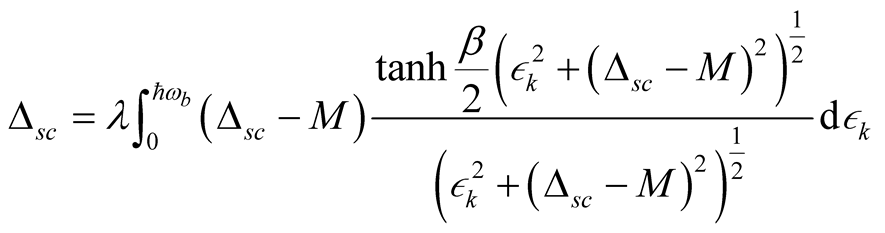 (16)
(16)
After rearranging equation (16), we get
 (17)
(17)
We consider the case, when , then the SDW can be expressed as
, then the SDW can be expressed as
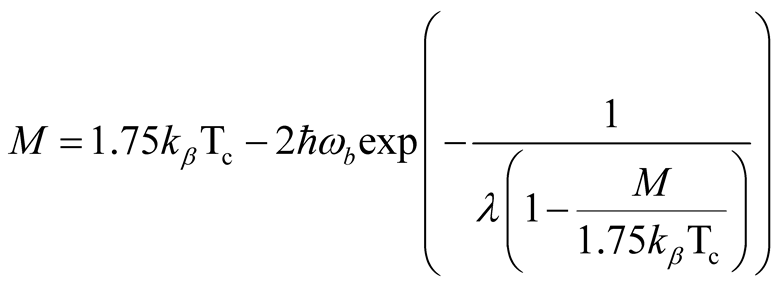 (18)
(18)
2.2. Dependence of SDW (M) on the SDW Transition Temperature (TSDW)
The equation of motion for the correlation  to express the order parameter of SDW can be described as:
to express the order parameter of SDW can be described as:
 (19)
(19)
Evaluating the commutation in equation (19), we obtain
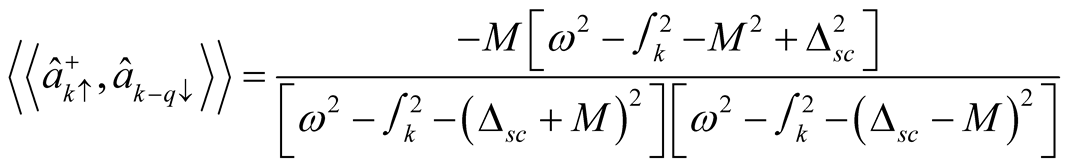 (20)
(20)
Using the expression  and Matsubara’s frequency, we get
and Matsubara’s frequency, we get
 (21)
(21)
Thus, the SDW order parameter is given by
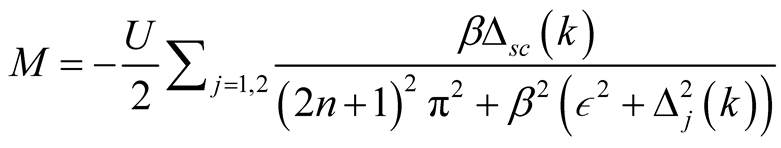 , (22)
, (22)
Using the equality relation in equation (14), the SDW order parameter can be expressed as
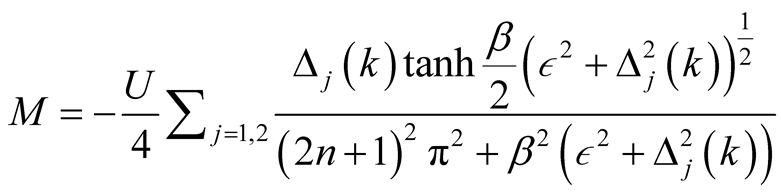 (23)
(23)
Changing of the summation into an integral by introducing the density of state , we obtained the expression for SDW order parameter as
, we obtained the expression for SDW order parameter as
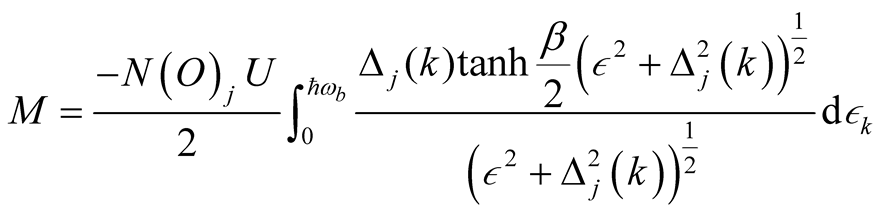 (24)
(24)
After simplifying the above equation, we obtained
 (25)
(25)

Figure 1. The Tc and TSDW vs. magnetic order parameter.
where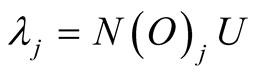 .
.
For very small value of  the second term of the RHS of equation (25) goes to zero. Thus, for
the second term of the RHS of equation (25) goes to zero. Thus, for  SDW transition temperature can be written as
SDW transition temperature can be written as
 (26)
(26)
3. Result and Discussion
Using the model of the Hamiltonian and green function formalism we obtained two important results expressed by Equations (18) and (26). We examined the effect of magnetic order parameter (M) on superconducting transition temperature (Tc) and magnetic order parameter (M) on spin density wave transition temperature (TSDW) in SmO1−xFxFeAs by using the results. Based on equation (18), we plotted the phase diagram of Tc versus M which shows that as the magnetic order parameter (M) increases the superconducting transition temperature (Tc) decreases. The phase diagram of magnetic ordering temperature (TSDW) versus magnetic ordering (M) is also plotted based on the equation (26). As we observed from this graph the magnetic transition temperature increases as the magnetic order parameter increases. Finally when phase diagram of Tc versus M and the phase diagram of TSDW versus M are merged an intersecting region in some range of order parameter is found as indicated in Figure 1.
4. Conclusion
Superconductivity and magnetism are antagonistic to each other. However, Muon spin rotation experiment has shown that these two stats coexist in SmO1−xFxFeAs. We are motivated by this experiment and use a model of Hamiltonian and employ green function formalism. We have got mathematical expressions for the order parameters. The intersection region we found under the superconducting critical temperature and SDW transition temperature vs. magnetic order parameter by using these results confirms that these two exclusive phenomena can coexist together in some range of magnetic order as demonstrated in Figure 1. Our theoretical predictions are in broad agreement with experimental finding.
References
- Kamihara, Y., Watanabe, T., Hirano, M. and Hosono, H. (2008) Iron-Based Layered Superconductor La[O1-xFx] FeAs (x = 0.05 0.12) with Tc = 26 K. Journal of the American Chemical Society, 130, 3296-3297.
- Chen, G.F., Li, Z., Wu, D., Li, G., Hu, W.Z., Dong, J., Zheng, P., Luo, J.L. and Wang, N.L. (2008) Superconductivity at 41°K and Its Competition with Spin-Density-Wave Instability in Layered CeO1-xFxFeAs. Physical Review Letters, 100, Article ID: 247002. http://dx.doi.org/10.1103/PhysRevLett.100.247002
- Takuji, N. (2014) Perturbation Theory of High-Tc Superconductivity in Iron Pnictides. Journal of the Physical Society of Japan. arXiv:0811.2462v1
- Zhang, H.-J., Xu, G., Dai, X. and Fang, Z. (2009) Enhanced Orbital Degeneracy in Momentum Space for LaOFeAs. Chinese Physics Letters, 26, Article ID: 017401. http://dx.doi.org/10.1088/0256-307X/26/1/017401
- Che, R.C., Wang, L., Chen, Z., Ma, C., Liang, C.Y., Lu, J.B., Shi, H.L., Yang, H.X. and Li, J.Q. (2008) Superconductivity in (La1-xCex)(O0.9F0.1)FeAs and La1-xPbx)OFeAs. EPL, 83, Article ID: 66005. www.epljournal.org
- Ren, Z.A., Lu, W., Yang, J., Yi, W., Shen, X.L., Li, Z.C., Che, G.C., Dong, X.L., Sun, L.L., Zhou, F. and Zhao, Z.X. (2008) Superconductivity at 55 K in Iron-Based F-Doped Layered Quaternary Compound Sm[O1-xFx]FeAs. Chinese Physics Letters, 25, 2215.
- Kenji, I., Yusuke, N. and Hideo H. (2009) To What Extent Iron-Pnictide New Superconductors Have Been Clarified. Journal of the Physical Society of Japan, 78, Article ID: 062001. http://dx.doi.org/10.1143/JPSJ.78.062001
- Kordyuk, A.A. (2012) Iron-Based Superconductors: Magnetism, Superconductivity, and Electronic Structure. Low Temperature Physics, 38, 1119-1134.
- Chubukov, A.V., Efremov, D.V. and Eremin, I. (2008) Magnetism, Superconductivity, and Pairing Symmetry in IronBased Superconductors. Physical Review B, 78, Article ID: 134512. http://dx.doi.org/10.1103/PhysRevB.78.134512
- Vorontsov, A.B., Vavilov, M.G. and Chubukov, A.V. (2010) Superconductivity and Spin-Density Waves in Multiband Metals. Physical Review B, 81, Article ID: 174538. http://dx.doi.org/10.1103/PhysRevB.81.174538
- Izyumov, Yu.A. and Kurmaev, E.Z. (2010) High-Tc Superconductors Based on FeAs Compounds. Springer-Verlag, Berlin Heidelberg.
- Drew, A.J., Niedermayer, Ch., Baker, P.J., Pratt, F.L., Blundell, S.J., Lancaster, T., Liu, R.H., Wu, G., Chen, X.H., Watanabe, I., Malik, V.K., Dubroka, A., Rossle, M., Kim, K.W., Baines, C. and Bernhard, C. (2009) Coexistence of Static Magnetism and Superconductivity in SmFeAsO1-xFx as Revealed by Muon Spin Rotation. Nature Materials, 8, 310-314. http://dx.doi.org/10.1038/nmat2396
- Zubarev, D.N. (1960) Double-Time Green Functions in Statistical Physics. Soviet Physics Uspekhi, 71, 71-116.

