World Journal of Condensed Matter Physics
Vol.4 No.1(2014), Article ID:42726,7 pages DOI:10.4236/wjcmp.2014.41002
Magnetometry and Hyperthermia Study of Magnetic Fluid Preparation UNIMAG
![]()
1Andronikashvili Institute of Physics, Ivane Javakhishvili Tbilisi State University, Tbilisi, Georgia; 2ATT Ltd., Scientific Laboratory “Magnetic Fluids in Medicine and Biology”, Tbilisi, Georgia; 3Natishvili Institute of Morphology, Ivane Javakhishvili Tbilisi State University, Tbilisi, Georgia; 4Ivane Javakhishvili Tbilisi State University, Tbilisi, Georgia.
Email: *mgrigor@rocketmail.com
Copyright © 2014 Grigor I. Mamniashvili et al. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited. In accordance of the Creative Commons Attribution License all Copyrights © 2014 are reserved for SCIRP and the owner of the intellectual property Grigor I. Mamniashvili et al. All Copyright © 2014 are guarded by law and by SCIRP as a guardian.
Received December 12th, 2013; revised January 14th, 2014; accepted January 26th, 2014
KEYWORDS
Magnetic Nanoparticles; Suspension; Hyperthermia; Magnetometry; NMR
ABSTRACT
We investigated the hyperthermal and magnetic properties of the stable magnetic suspension of magnetite nanoparticles. With this purpose in mind, we designed a low-frequency oscillator, 300 W, 300 KHz. A sample of the magnetic suspension was placed in the induction coil and heated up to 55˚C for 30 minutes. Based on the results of measurements of transverse susceptibility, we can infer that the suspension was superparamagnetic at room temperature and transformed into the magnetic state at nitrogen temperature. Comparing the obtained experimental results with the literature data, we assessed the mean size of nanoparticles, which made up about 10 nm. Computer simulation assessment on the basis of magnetization curve gives close results.
1. Introduction
As is known, the normal human body temperature is 37˚C. However, healthy cells can preserve their viability at the temperature of up to 42˚C. The fact is that the cancer cells are heated stronger than healthy ones and die prior to healthy cells, because they remove heat less effectively, which results in their overheating. Cancer treatment by hyperthermia consists in increasing artificially the temperature in the tumor up to 42˚C - 45˚C, which results in the death of carcinogenic cells. This approach allows one to destroy the tumor, at the same time minimizing the damage to healthy tissue and thus limiting the negative side effects of treatment by hyperthermia.
Currently, hyperthermia is often used in combination with radiotherapy and chemotherapy, as the hyperthermia effect on cancer cells makes them less stable with respect to chemical and radiation therapies. Hyperthermia effects may be applied both to a separate tumor localized on the surface or in the depth of the human body and the whole body.
Previously, for local hyperthermia, microwave, laser and ultrasound radiation were used. With a large tumor development throughout patient’s body, the whole body is exposed to elevated temperatures up to 45˚C in a special thermal camera.
Local hyperthermia can effectively heat the tumor. However, it is necessary to provide the conditions when the adjacent healthy tissues are not exposed to elevated temperatures over 42˚C, which may cause damage. This indicates the need for precise control of the local temperature of the body for the hyperthermia treatment process. The effectiveness of hyperthermia is affected by the ability of microwave, laser and ultrasound radiation of penetrating efficiently into body tissues; otherwise, it would be difficult to expose to the treatment deeply located tumors, for example, in the brain or pelvis of a patient.
The possibility of cancer treatment by local hyperthermia has led to the development of devices for the local heating of tumors without affecting significantly the surrounding healthy tissues. One of the most promising directions associated with the use of magnetic materials for hyperthermia was proposed by Gilchrist et al. in 1957 [1].
The ferroand ferrimagnetic nanoparticles used for implantation possessed a magnetic moment even in the absence of a magnetic field. By using the alternating magnetic field, one can change the magnetic moment direction both due to the physical rotation of magnetic nanoparticles overcoming the force of friction or viscosity of the environment, and due to the reorientation of the magnetic moment, using the energy of the magnetic field. This energy then dissipates in the heat energy [2]. Just, this energy is used to destroy cancer tissues during hyperthermia.
The dissipation of magnetic energy occurs when the magnetic nanoparticles return into equilibrium with their physical rotation overcoming the force of viscosity due to the reorientation of the magnetic moment only. This explains the existence of two, Brownian and Neel, mechanisms of dissipation of magnetic energy, respectively [3]. Among them, the Neel relaxation is more effective to heat the tumor.
In papers [3,4], the processes of heating using magnetic nanoparticles were described in detail. As known [5], the magnetic nanoparticles 10 nm or less in size exhibit superparamagnetic properties. As temperature decreases below the Curie or Neel points of ferroand ferromagnetic transitions, the transition from the paramagnetic state to magnetically ordered ferromagnetic or ferrimagnetic states occurs in magnetic materials. If the linear dimensions of the particles of these materials are within 1 - 10 nm, their preferred directions of magnetization would change chaotically at the temperature below the Curie and Neel points and above so-called blocking temperature TB because of the thermal fluctuation like change the magnetic moment directions in paramagnets under the influence of thermal motion. It must be born in mind that the superparamagnetic particle is in a singledomain state, as domain walls are energetically unfavorable for such small particles. As a result, the system of superparamagnetic particles behaves in the magnetic field and at temperature changes like paramagnetic gas of N atoms, where N is the number of single-domain superparamagnetic particles, each of which has a magnetic moment M. For this system, the magnetization varies by the Curie law in weak magnetic fields and by the Langevin formula in the range of magnetic saturation.
The magnetization of superparamagnets is much higher than conventional paramagnetic magnetization. For the chaotic changes in the spatial orientation of the magnetic moment of nanoparticles, it is necessary that the energy of thermal motion kT (k is the Boltzmann constant, T— temperature) was greater than the energy of magnetic anisotropy of particles KV (where K is the anisotropy constant, V is the particle volume).
When the temperature drops below the blocking temperature TB, specific for each material and particle dimensions, the change of the magnetization direction of particles ceases to be chaotic, and the particles behave as usual coarse-grain magnets. Examples of these superparamagnetic particles are small particles of Co, Fe, Ni and some iron oxides such as magnetite, Fe3O4, etc. Because the magnetic moments of superparamagnetic particles have random orientations under the influence of thermal fluctuations of the environment, they do not have the resultant magnetic moment in the absence of an external magnetic field. In contrast to the conventional magnetic particles, they do not aggregate after removal of the external magnetic field [6]. The aggregation of magnetic particles can hamper their removal from the body after application. Therefore, the superparamagnetic particles have great advantages as agents for the treatment of cancer by hyperthermia. Such particles are readily absorbed by cancer cells 10 - 100 μm in diameter. This improves significantly the effectiveness of hyperthermia when applied to cancer cells. The superparamagnetic nanoparticles can also efficiently overcome the blood-brain barrier, which is essential for the treatment of brain tumors [7]. Furthermore, the nanoparticles may be coupled with viruses (20 - 450 nm), proteins (5 - 50 nm) and genes (length of 10 - 100 nm) [3].
Hyperthermia of cancer using a magnetic fluid is carried out by direct administration of the liquid containing magnetic nanoparticles to the tumor.
When exposed to a low-frequency alternating magnetic field, the nanoparticles generate heat that destroys the tumor. Unlike the laser, microwave and ultrasound hyperthermia, this procedure is minimally invasive. Thus, there is no undue heating of healthy tissues, as only the magnetic nanoparticles absorb the energy of the magnetic field.
Magnetic fluids are typically stable colloid systems in aqueous solutions and other biocompatible solvents [8].
Innovation Bio-Medical Technologies Inc. (IBMT), Canada, used clinically magnetite nanoparticles for identification and surgical removal of sentinel lymph nodes (the lymph nodes that breast cancer first metastasizes to). A preparation of magnetite nanoparticles under the trade name of Unimag was used as a visual contrast agent for breast cancer in Georgia [9-12]. Magnetic fluid preparation Unimag represents a stable 2.5% suspension of magnetite nanoparticles. Active components of preparation Unimag are magnetite (Fe3O4) nanoparticles obtained by sedimentation of the solution of the salts of 2- and 3- valent iron, which are 5 - 10 nm in size and have a spherical form [13-15].
The objective of this work is to determine if the Unimag magnetite nanoparticles can be heated by using the alternating magnetic field with the aim of destroying the lymph nodes without invasive surgery.
To implement this aim, the magnetic properties of Unimag were studied by using the precise resonance method for measurement of transverse susceptibility of the suspension, as well as the vibrating sample magnetometer (VSM) technique. These methods in combination with literature data make it possible to evaluate the mean size of nanoparticles.
To determinate the hyperthermia properties of Unimag preparation, we designed a low-frequency generator (with RF power of 300 W and resonance frequency of 300 KHz).
2. Experimental Results and Discussion
2.1. Measurement of Transverse Susceptibility by Using the LC-Generator
The circuit based on the LC-resonance generator (Figure 1) was used for the measurement of transverse susceptibility of magnetic fluids.
The ampoule containing the magnetic fluid was placed into the induction coil of the LC-generator. The variations of its resonance frequency were measured at the variations in the external magnetic field HDC, which was perpendicular to the coil field HRF.
The standard representation of the frequency of acceptor oscillations looks like
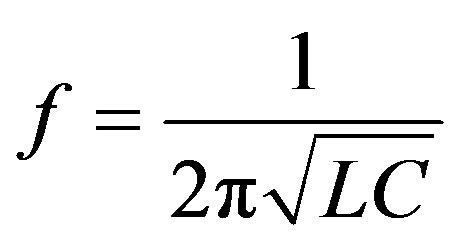 , (1)
, (1)
where L is the coil inductance, and C is the capacitor capacity.
Placement of the sample into the induction coil changed the inductance value by ΔL. If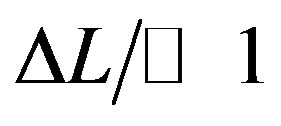 , by differenciating Equation (1), we get
, by differenciating Equation (1), we get
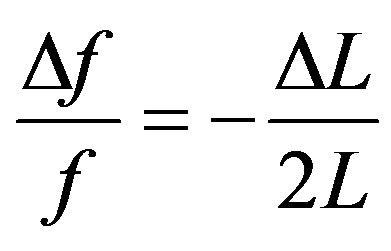
The inductance variations are connected with the changes in material properties. In the case of the magnet, the inductance variation is proportional to the variation in the real part of complex susceptibility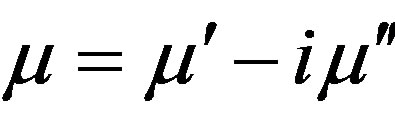 . Hence, it turned out that ΔL ~
. Hence, it turned out that ΔL ~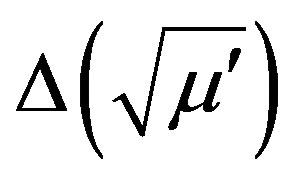 and
and
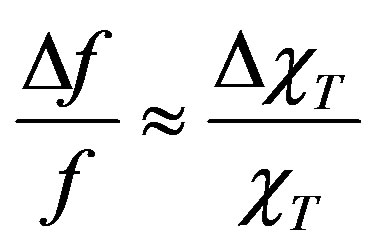
It is very important that this device was successfully used for investigation of the fields of magnetic anisotropy HK of superparamagnetic nanoparticles in the test sample. To this effect, the sample was placed into the induction coil of the LC-generator for measurement of

Figure 1. LC-generator circuit.
transverse susceptibility χT at the variation in the external static field. In this device, the oscillating magnetic field of fixed amplitude (~5 Oe, 10 MHz) is applied perpendicularly to the external field. The resonance frequency shift at variations in the external field or temperature characterizes the variation in the transverse susceptibility χT of the sample. The typical dependence of χT on the external magnetic field shows the peaks that are determined by the distribution of anisotropic fields HK of nanoparticles (Figure 2, curve 1). The changes in the positions of these peaks depending on the magnetic field and temperature allow better understanding of the fundamental properties of this system.
Figure 2 shows the ∆cT/cT (%) ratio dependence on magnetic field H taken from work [16] for Fe3O4 magnetite powder with the mean grain size of ~6 nm at the temperature higher (1) and lower (2) than the blocking temperature when the powder becomes magnetic (T = 300 K and 10 K, respectively). In work [16], similarly to our device, the LC-generator based on the CMOS oscillator circuit was used.
In Figures 3(a) and (b) are shown the results of measurements of the LC-generator frequency with the Unimag sample depending on the external field at its variations from zero to 1.4 T (tesla) (14 kOe) and inversely, T = 300 K (a) and T = 77 K (b).
It is evident that the Figure 3(a) corresponds to the superparamagnetic state of the sample (without hysteresis), while the Figure 3(b) corresponds to the magnetic one. At the same time, from Figure 3(b) it is seen that the value of the field of magnetic anisotropy for the Unimag sample should be of the order of 600 Oe. Hence, we can infer that, in our case, the mean grain size is somewhat larger than in the magnetite sample [16] and is apparently close to 10 nm.
The magnetometry measurements of Unimag suspension were performed by using VSM (Cryogenic Limited, UK) allowing one to carry out the measurements over the temperature range 1.7 - 293 K and at magnetic fields up to 5 T.
Figure 4 shows the results of hysteresis curve measurements at room temperature confirming the superparamagnetic behavior of the suspension at this temperature, which is in agreement with the measurements by the RF resonance method.

Figure 2. Typical dependence of the transverse susceptibility (χT) on the external magnetic field.
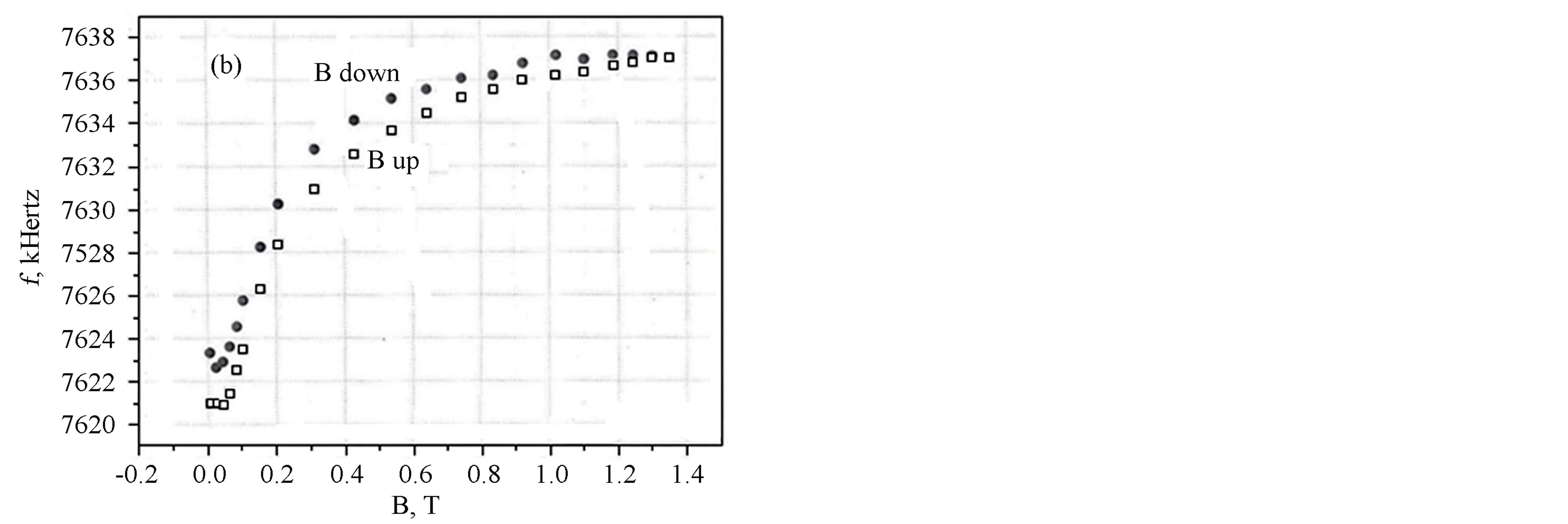
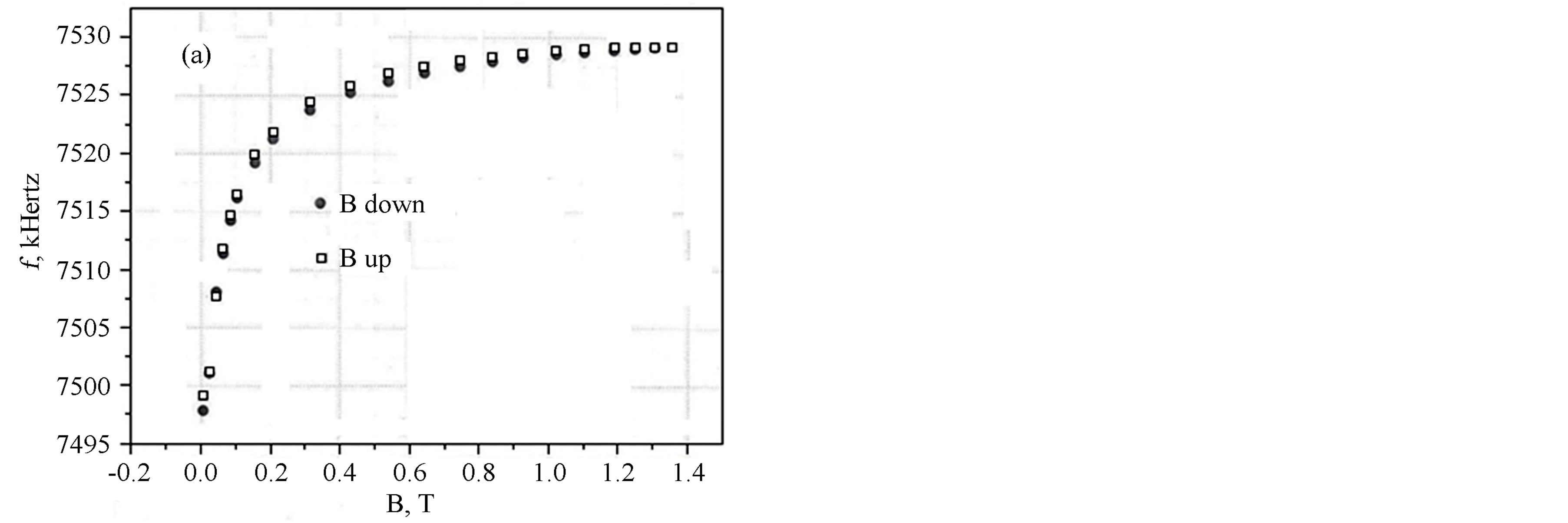
Figure 3. LC generator frequency with the “Unimag” sample dependence on the external magnetic field at room temperature (a), and at liquid nitrogen temperature (b).
2.2. Hyperthermia Experiment
The suspension poured into a test tube 15 cm long where an alcoholic thermometer was placed was used for the experiment. This system was placed into a remote inductor. The outer diameter of the induction coil was d = 45 mm, and its height was h = 50 mm; the coil was wound from a copper tube 5 mm thick. The time dependence of temperature t˚C = f(T) was taken in the optimal mode of the resonance inductor.
For performing the hyperthermia experiments with small biological objects, we used above mentioned low-
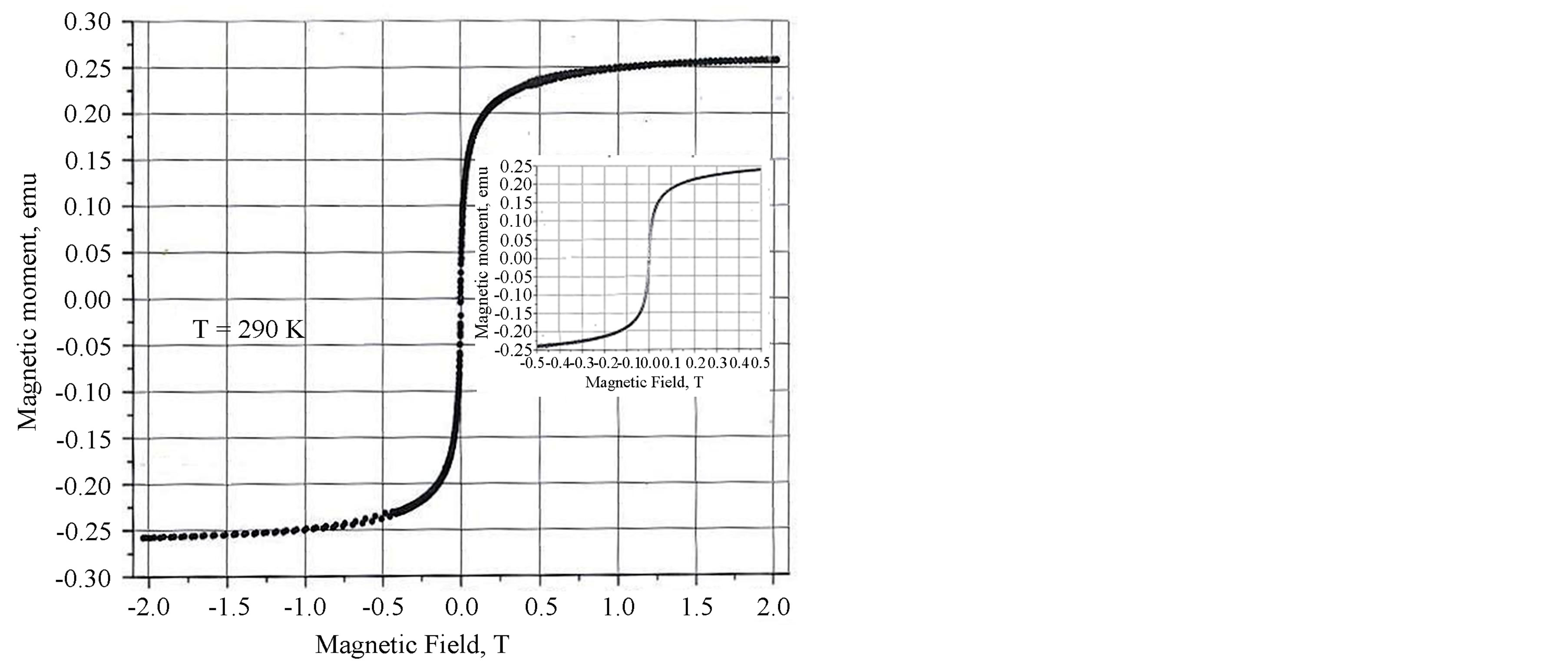
Figure 4. Magnetization curve for “Unimag” preparation.
frequency (LF) generator which allowed us to increase the suspension temperature up to 55˚C (Figure 5).
2.3. Estimation of the Magnetic Nanoparticle Distribution on the Basis of the Magnetization Curve
The estimation of the size distribution of magnetic nanoparticles (MNP) by their magnetic properties has become a popular subject during recent years. For instance, in [17, 18] the sizes of MNP were studied by small-angle neutron scattering, in [19]—by thermomagnetic measurements, and in [20]—by magnetic susceptibility, while in [21,22] the size distribution of magnetic nanoparticles was studied by using modified magnetization curves.
We present the construction of the size distribution of MNP by their magnetization curves using the Tikhonov regularization method for ill-posed equations for magnetization [23-27]. The magnetization curve was obtained from a water-based Fe3O4 MNP sample (preparation Unimag).
Agglomeration and sedimentation of MNP during magnetic measurements has an adverse impact on the size distribution assessment. Physical vibration prevents aggregation and sedimentation during the experiment or makes them insignificant. Therefore, for the magnetization measurements, a vibrating sample magnetometer (VSM) was used. The VSM is effective due to the continuous sample vibration during the experiment, and the obtained NMR magnetization curve does not require further adjustment. The experimental magnetization curves are shown in Figure 4.
We used the method of determination of the MNP sizes from magnetic measurements. By comparing the modified Langevin curve with the observed magnetization curve, we obtained the size-distribution function of MNPs and determined the average particle size. A similar method

Figure 5. Temperature change in the suspension placed in the output resonator of the LF generator, measured with an alcohol thermometer.
was first used for small ferromagnetic particles in [28].
The magnetization curve is the result of simultaneous action of the magnetic field and the thermal motion. For a multiple-sized system of non-interacting particles, the mean magnetization could be expressed in the following way [29-32]
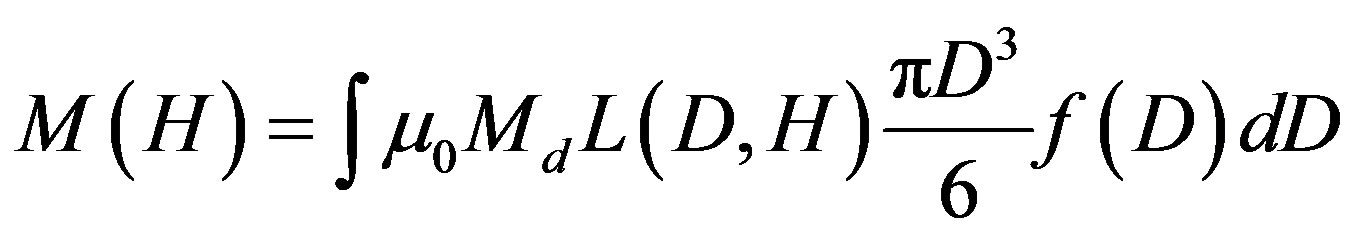
where L is the Langevin function; D is the mean diameter of MNPs; f is the function of particle size distribution; Md is the saturation magnetization; H is the magnetization field value.
As it obvious, in the MNP model, the mathematical expression of magnetization is the function of particle size distribution.
The degree of MNP magnetization affects significantly the particle size distribution f(D).
Berkov [30,31] discretized the equation and obtained a numerical matrix. If the particle diameter D and magnetic field H are discrete values, the magnetization equation will take the form [30,31].
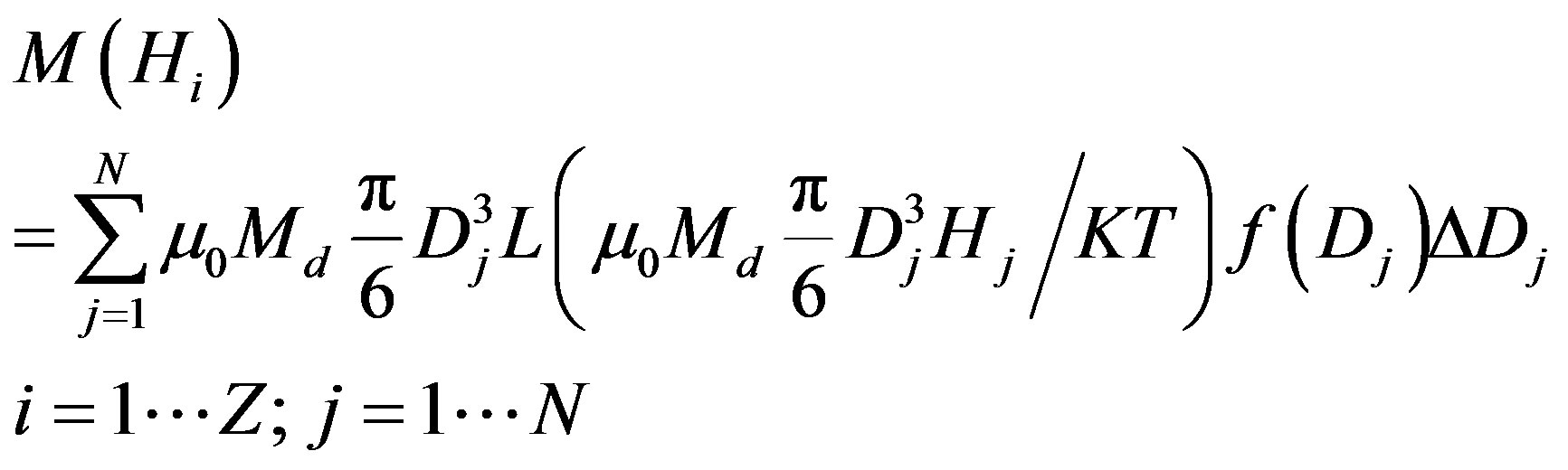 where N is the designation of the number of sampling points for particle diameters and Z is the sampling step for the magnetization field Hi. The magnetic moment matrix could be rewritten in the following way
where N is the designation of the number of sampling points for particle diameters and Z is the sampling step for the magnetization field Hi. The magnetic moment matrix could be rewritten in the following way
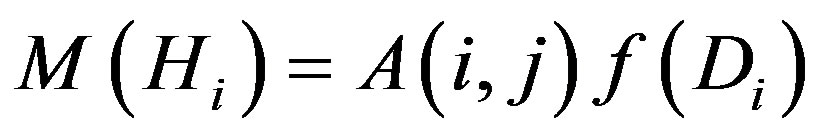
where
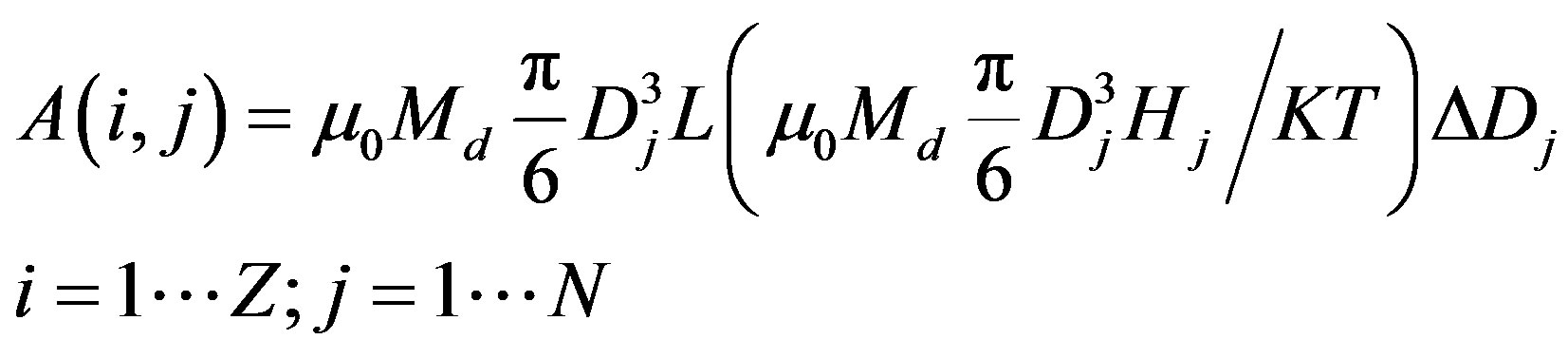
where A(i, j) could be determined from the MNP magnetization by the Langevin formula, M(i) corresponds to the magnetization curve and f(j) is the function of the particle size distribution. The details of sampling and its influence on the ill-posed matrix equation and also the discussion of particle size and magnetization ranges, used in the analysis, are described in [22]. All terms of Equation (1) are non-negative. As a function of particle size distribution f(j) is a single unknown term, the evaluations of particle size distribution could be reduced to the solution of the non-negative matrix equation.
System of Equations (2) is ill-posed. This means that the errors of matrix coefficients and free terms or the rounding errors in the calculation could strongly distort the solution. It is necessary to regularize the original problem. The regularization in mathematics and information means the introduction of additional information for solving the problem. The simple form of integral equation regularization was developed by A. N. Tikhonov [23-26]. The approximate solution should be defined so that it is stable under small changes of the original information.
The solution to the matrix equation is complicated by artificial oscillations [20,30,31] that always appear in the solutions of ill-posed matrix equations. The use of the Tikhonov regularization method made it possible to overcome these oscillations and to obtain sufficiently accurate and stable solutions. The essence of the method is as follows.
The resulting system of equations could be written in a simplified form:
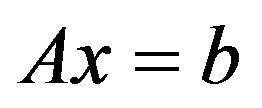 (2)
(2)
If the system is ill-posed, the rounding errors of calculation could also strongly distort the solution. It is necessary to regularize the initial problem. To this effect, instead of the considered initial problem, let us consider the following one:
 (3)
(3)
where АТ is the transposed matrix; Е is the identity matrix; a is the positive parameter;  is the symmetric matrix. For the concrete values of a, it is solved by the square root method. If a = 0, system of Equation (3) coincides with ill-posed system. At large values of a, regularized system (3) is well-posed, but the solution хa will not be close to the solution sought-for. It is obvious that the best would be the lowest value of a, at which conditioning of the system is still satisfactory, which is checked by visual monitoring and verification of the residual
is the symmetric matrix. For the concrete values of a, it is solved by the square root method. If a = 0, system of Equation (3) coincides with ill-posed system. At large values of a, regularized system (3) is well-posed, but the solution хa will not be close to the solution sought-for. It is obvious that the best would be the lowest value of a, at which conditioning of the system is still satisfactory, which is checked by visual monitoring and verification of the residual .
.
Figure 6 shows the obtained function of MNP size distribution.
From Figure 6 it is evident that there are two peaks with mean diameters about 6.7 and 9.8 nm. It should be noted that the given distribution differs from the log-
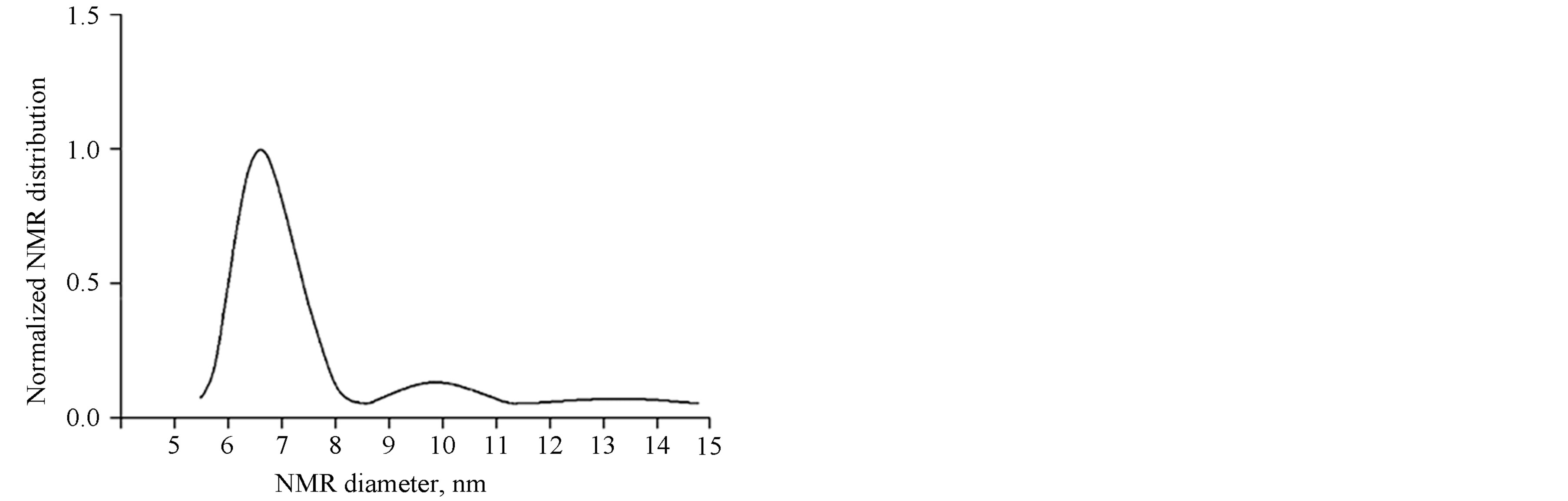
Figure 6. Size distribution of MNP solutions obtained by using the Tikhonov regularization method for colloid preparation Unimag.
normal one which is the characteristic of MNP. It can be assumed that the cause of it is a small primary aggregation of dispersible particles. The left peak corresponds to the separate NMP, while the right one can be caused by clusters. By the evaluation of the area under peaks, one can define the fractions of magnetic particles of each type. The second-type particles make up less than 10%. Hence it follows that separate nanoparticles play the main role in the magnetization curve formation.
The investigations are under way for MNPs of different materials.
3. Conclusion
In this work, hyperthermia and magnetic measurements on preparation Unimag were performed. It is shown that, by using the home made simple low-frequency generator, with 300 W power and 300 kHz frequency, it is possible to heat the fluid up to 55˚C for 30 minutes. The measurements of fluid magnetic properties verified that, at room temperature, the magnetite nanoparticles in the suspension were in the superparamagnetic state and their mean size was about 10 nm. The computer simulation results on the mean magnetic nanoparticle size based on the magnetization curve are close to the experimental data.
REFERENCES
- R. K. Gilchrist, R. Medal, W. D. Shorey, R. C. Hanselman, J. C. Parrott and C. B. Taylor, “Selective Inductive Heating of Lymph Nodes,” Annals of Surgery, Vol. 146, No. 4, 1957, pp. 596-606. http://dx.doi.org/10.1097/00000658-195710000-00007
- R. Hergt, W. Andra, C. G. D’Ambly, I. Hilger, W. A. Kaiser, U. Richter and H.-G. Schmidt, “Physical Limits of Hyperthermia Using Magnetite Fine Particles,” IEEE Transactions on Magnetics, Vol. 34, No. 5, 1998, pp. 3745-3754. http://dx.doi.org/10.1109/20.718537
- Q. A. Pankhurst, J. Connolly, S. K. Jones and J. Dobson, “Applications of Magnetic Nanoparticles in Biomedicine,” Journal of Physics D: Applied Physics, Vol. 36, No. 13, 2003, pp. R167-R181. http://dx.doi.org/10.1088/0022-3727/36/13/201
- Q. A. Pankhurst, N. T. K. Thanh, S. K. Jones and J. Dobson, “Progress in Applications of Magnetic Nanoparticles in Biomedicine,” Journal of Physics D: Applied Physics, Vol. 42, No. 22, 2009, 15 p.
- G. C. Papaefthymiou, “Nanoparticle Magnetism,” Nano Today, Vol. 4, No. 5, 2009, pp. 438-447. http://dx.doi.org/10.1016/j.nantod.2009.08.006
- C. C. Berry and A. S. G. Curtis, “Functionalisation of Magnetic Nanoparticles for Applications in Biomedicine,” Journal of Physics D: Applied Physics, Vol. 36, No. 13, 2003, pp. R198-R206. http://dx.doi.org/10.1088/0022-3727/36/13/203
- J. M. Koziara, P. R. Lockman and R. J. Mumper, “In Situ Blood-Brain Barrier Transport of Nanoparticles,” Pharmaceutical Research, Vol. 20, No. 11, 2003, pp. 1772- 1778. http://dx.doi.org/10.1023/B:PHAM.0000003374.58641.62
- P. Tartaj, M. del Puerto Morales, S. Veintemillas-Verdaguer, T. González-Carreño and C. J. Serna, “The Preparation of Magnetic Nanoparticles for Applications in Biomedicine,” Journal of Physics D: Applied Physics, Vol. 36, No. 13, 2003, pp. R182-R197. http://dx.doi.org/10.1088/0022-3727/36/13/202
- R. Lutidze, B. Tkeshelashvili, G. Burkadze and B. V. Surguladze, “The Echo-Contrasting Ability of the Medical Magnetic Fluid Unimag and Its Peculiarities During the Elimination from the Body in an Experiment,” Georgian Medical News, Vol. 152, No. 11, 2007, pp. 60-63.
- B. Surguladze, Z. Zautashvili, G. Burkadze, Sh. Gelashvili, N. Gribanov and T. Tskitishvili, “New Method of Sentinel Lymph Node Detection in Malignant Tumors by Using the Preparation Unimag,” Proceedings of the 6th International Conference on Scientific and Clinical Applications of Magnetic Carriers, 2006 (Poster presentation). http://www.magneticmicrosphere.com/meetings/meet2006/posters.php
- B. Surguladze, R. Zhorzoliani and T. Tskitishvili, “Novel Method of Sentinel Lymph Node Detection in Malignant Tumors Using Preparation UNIMAG,” Magnetic Fluids in Medicine and Biology, ATT Ltd., Georgia, Breast Cancer Research, 2007, p. 15. http://dx.doi.org/10.1186/bcr1721
- B. Surguladze, A. Baghishvili, T. Tskitishvili and N. Gribanov, “Ultrasound Imaging of Sentinel Lymph Nodes in the Patients with Breast Cancer by Using the Preparation Unimag,” Proceedings of the 7th International Conference on Scientific and Clinical Applications of Magnetic Carriers, 2008, (Oral Presentation). http://www.magneticmicrosphere.com/meetings/meet2008/index.php
- W. C. Elmore, “The Magnetization of Ferromagnetic Colloids,” Physical Reviews, Vol. 54, No. 12, 1938, pp. 1092- 1095. http://dx.doi.org/10.1103/PhysRev.54.1092
- N. M. Gribanov, E. E. Bibik, O. V. Buzunov and V. N. Naumov, “Physicochemical Regularities of Obtaining of Highly Dispersed Magnetite by the Method of Chemical Condensation,” Journal of Magnetism and Magnetic Materials, Vol. 85, No. 1-3, 1990, pp. 7-10. http://dx.doi.org/10.1016/0304-8853(90)90005-B
- B. E. Kashevsky, V. E. Agabekov, S. B. Kashevsky, K. A. Kekalo, E. Yu. Manina, I. V. Prokhorov and V. S. Ulashchik, “Study of Cobalt Ferrite Nanosuspensions for LowFrequency Ferromagnetic Hyperthermia,” Particuology, Vol. 6, No. 5, 2008, pp. 322-333. http://dx.doi.org/10.1016/j.partic.2008.07.001
- A. L. Figueroa, J. Bartolomé, J. M. García del Pozo, A. Arauzo, E. Guerrero, P. Téllez, F. Bartolomé and L. M. García, “Low-Temperature Radio-Frequency Transverse Susceptibility Measurements Using a CMOS Oscillator Circuit,” Journal of Magnetism and Magnetic Materials, Vol. 324, No. 17, 2012, pp. 2669-2675. http://dx.doi.org/10.1016/j.jmmm.2012.03.058
- V. I. Petrenko, V. L. Aksenov, M. V. Avdeev, L. A. Bulavin, L. Rosta, L. Vekas, V. M. Garamus and R. Willumeit, “Analysis of the Structure of Aqueous Ferrofluids by the Small-Angle Neutron Scattering Method,” Physics of the Solid State, Vol. 52, No. 5, 2010, pp. 974-978. http://dx.doi.org/10.1134/S1063783410050185
- M. V. Avdeev, V. L. Aksenov and A. V. Feoktystov, “On Determination of ‘Atomic’ and ‘Magnetic’ Sizes of Nanoparticles in Ferrofuids by Means of Small-angle Neutron Scattering,” Communication of the Joint Institute for Nuclear Research, Dubna, 2011.
- R. S. DiPietro, H. G. Johnson, S. P. Bennett, T. J. Nummy, L. H. Lewis and D. Heiman, “Determining the Magnetic Nanoparticle Size Distributions from Thermomagnetic Measurements,” Applied Physics Letters, Vol. 96, No. 22, 2010, 3 p.
- K. Enpuku, T. Tanaka, Y. Tamai, F. Dang, N. Enomoto, J. Hojo, H. Kanzaki and N. Usuki, ”Size Distribution of Magnetic Marker Estimated from AC Susceptibility in Solution for Biosensor Application,” Japanese Journal of Applied Physics, Vol. 47, No. 10, 2008, pp. 7859-7865. http://dx.doi.org/10.1143/JJAP.47.7859
- W. Liu, M. Zhou and L. Kong, “Estimation of the Size Distribution of Magnetic Nanoparticles Using Modified Magnetization Curves,” Measurement Science and Technology, Vol. 20, No. 12, 2009, pp. 125802-125809. http://dx.doi.org/10.1088/0957-0233/20/12/125802
- M. Zhou, W. Liu and L. Kong, “Estimation of Magnetic Nano-Particles Size Distribution Using Their Magnetization Curve,” Proceedings of the 5th International Symposium on Instrumentation Science and Technology, 2009, pp. 71334M1-71334M7.
- A. N. Tikhonov, “Solution of Incorrectly Formulated Problems and the Regularization Method,” Soviet Mathematics Doklady, Vol. 4, No. 4, 1963, pp. 1035-1038.
- A. N. Tikhonov, “Regularization of Incorrectly Posed Problems,” Soviet Mathematics Doklady, Vol. 4, No. 6, 1963, pp. 1624-1627.
- А. N. Tikhonov and V. Y. Arsenin, “Solutions of Ill-Posed Problems,” Wiley, New York, 1977.
- A. N. Tikhonov, A. V. Goncharsky, V. V. Stepanov and A. G. Yagola, “Numerical Methods for the Solution of IllPosed Problems,” Academic Publishers, Kluwer, 1995. http://dx.doi.org/10.1007/978-94-015-8480-7
- N. S. Bakhvalov, N. P. Jidkov and G. М. Kobelkov, “Numerical methods,” Nauka, Moscow, 1987.
- G. P. Bean and I. S. Jacobs, “Magnetic Granulometry and Super Paramagnetism,” Journal of Applied Physics, Vol. 7, No. 12, 1956, pp. 1448-1452. http://dx.doi.org/10.1063/1.1722287
- R. E. Rosensweig, “Ferrohydrodynamic,” Cambridge University Press, Cambridge, 1985.
- E. Romanus, D. V. Berkov, S. Prass, C. Gross, W. Weitschies and P. Weber, “Determination of Energy Barrier Distributions of Magnetic Nanoparticles by Temperature Dependent Magnetorelaxometry,” Nanotechnology, Vol. 14, No. 12, 2003, pp. 1251-1254. http://dx.doi.org/10.1088/0957-4484/14/12/003
- G. F. Berkov, P. Görnert, N. Buske, C. Gansau, J. Mueller, M. Giersig, W. Neumann and D. Su, “New Method for the Determination of the Particle Magnetic Moment Distribution in a Ferrofluid,” Journal of Physics D: Applied Physics, Vol. 33, No. 4, 2000, pp. 331-337. http://dx.doi.org/10.1088/0022-3727/33/4/303
- V. D. Goya, T. S. Berquo, F. C. Fonseca and M. P. Morales, “Static and Dynamic Magnetic Properties of Spherical Magnetite Nanoparticles,” Journal of Applied Physics, Vol. 94, No. 5, 2003, pp. 3520-3528. http://dx.doi.org/10.1063/1.1599959
NOTES
*Corresponding author.

