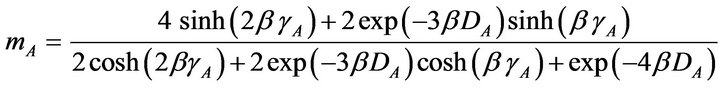World Journal of Condensed Matter Physics
Vol.3 No.2(2013), Article ID:31665,8 pages DOI:10.4236/wjcmp.2013.32018
Magnetic Properties of a Mixed-Spin-3/2 and Spin-2 Ising Ferrimagnetic System in an Applied Longitudinal Magnetic Field
![]()
Department of Physics, Faculty of Science, Almergeb University, Zliten, Libya.
Email: dr_fathiomar@yahoo.com
Copyright © 2013 Fathi Abubrig. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Received December 27th, 2012; revised February 26th, 2013; accepted March 18th, 2013
Keywords: Mixed-Spin; Ising; Susceptibility
ABSTRACT
The magnetic properties of a mixed Ising ferrimagnetic system consisting of spin-3/2 and spin-2 with different single ion anisotropies and under the effect of an applied longitudinal magnetic field are investigated within the mean-field theory based on Bogoliubov inequality for the Gibbs free energy. The ground-state phase diagram is constructed. The thermal behaviours of magnetizations and magnetic susceptibilities are examined in detail. Finally, we find some interesting phenomena in these quantities, due to applied longitudinal magnetic field.
1. Introduction
Recently, there have been many theoretical studies of mixed-spin Ising ferrimagnetic systems. These systems have been of interest because they have less translational symmetry than their single-spin counterparts, since they consist of two interpenetrating unequivalent sublattices. For this reason, They are studied not only for purely theoretical interest but also because they have been proposed as possible models to describe a certain type of ferrimagnetic systems such as molecular-based magnetic materials [1-3] which are of current interest. Moreover, the increasing interest in these systems is mainly related to the potential technological applications of these systems in the area of thermomagnetic recording [4,5]. Therefore, the synthesis of new ferrimagnetic material is an active field in material science.
One of these models to be studied was the mixed-spin Ising system consisting of spin-1/2 and spin-S (S > 1/2) in uniaxial crystal field. The model for different values of S (S > 1/2) has been investigated by exact on honeycomb lattice [6-8], as well as on Bethe lattice [9,10], mean-field approximation [11], effective-field theory with correlations [12-16], cluster variational theory [10], renormalization-group technique [17] and Monte-Carlo simulation [18-20]. On the other hand, ferromagnetic and ferrimagnetic systems subjected to longitudinal magnetic fields have been investigated for many years [21-23]. The results assured that the longitudinal magnetic field has strong effects on the magnetic properties of these systems. Subsequently, the attention has been devoted to mixed-spin systems in a longitudinal field theoretically. The magnetic properties of the mixed spin-1/2 and spin-1 Ising ferromagnetic system with a crystal-field interaction in the presence of a longitudinal magnetic field by using the cluster variational method was investigated by Ekiz and Keskin [24]. Wei et al. [25] studied the magnetic properties of a mixed spin-1/2 and spin-3/2 Ising model in a longitudinal magnetic field within the framework of EFT with correlations. They examined the thermal behaviours of the magnetizations, susceptibilities and phase diagrams in detail. The magnetic properties of a mixed spin-1/2 and spin-3/2 Ising system in a longitudinal magnetic field on a Bethe lattice were studied by using the recursion relation scheme [26]. The thermodynamic and magnetic properties of a mixed Ising system on a triangular array in the presence of longitudinal magnetic field were investigated by Aouzi et al by using EFT with correlations [27]. Jiang and Bai also studied the influences of an external longitudinal magnetic field on the magnetic properties of mixed spin-1/2 and spin-3/2 Ising ferromagnetic or ferrimagnetic bilayer system [28]. The Magnetic properties of an anti-ferromagnetic and ferrimagnetic mixed spin-1/2 and spin-5/2 Ising model in the longitudinal magnetic field and the Magnetic Properties of a Mixed Spin-3/2 and Spin-2 Ising Ferrimagnetic System within the Effective-field Theory are studied by Bayram Deviren et al by using the effective-field theory with correlations [29,30] and the results show that the longitudinal magnetic field plays an important role in the magnetic properties of the mixed spin Ising systems.
In this paper, our aim is to investigate the magnetic properties of the mixed spin-3/2 and spin-2 Ising system in the presence of longitudinal magnetic field within the framework of the mean-field theory based on Bogoliubov inequality for the Gibbs free energy. The outline of this work is as follows. In Section 2, we define the model and present the mean-field theory based on Bogoliubov inequality for the Gibbs free energy for the mixed-spin system with the applied longitudinal magnetic field. In Section 3, we discuss the temperature dependences of the sublattice and total magnetizations and sublattice and total susceptibilities for selected values of single-ion anisotropies. Finally, In Section 4 we present our conclusions.
2. Formulation of the Model and Its Mean-Field Solution
We consider a mixed spin-3/2 and spin-2 Ising model consisting of two sublattices A and B, which are arranged alternately. In this system, the sites of sublattice A are occupied by spin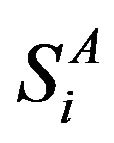 , which take spin values ±3/2 and ±1/2, while those of the sublattice B are occupied by spins
, which take spin values ±3/2 and ±1/2, while those of the sublattice B are occupied by spins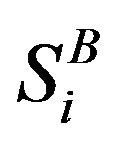 , which take spin values ±2, ±1 and 0. The Hamiltonian of the system is given by
, which take spin values ±2, ±1 and 0. The Hamiltonian of the system is given by
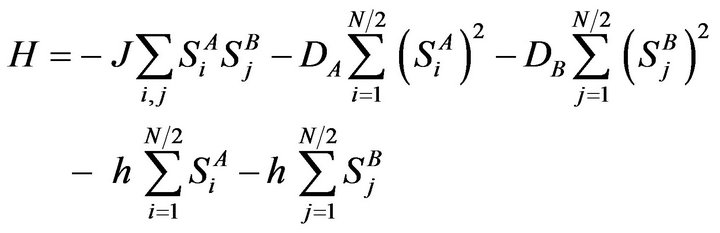 (1)
(1)
where 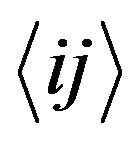 indicates a summation over all pairs of nearest-neighboring sites and the first summation is carried out only over nearest neighbour pairs of spins on different sublattices and J (J < 0) is the nearest-neighbour exchange parameter, DA is the crystal field interaction constant of spin-2 ions and DB is that of spin-3/2 ions. h is the external magnetic field acting on the lat tice.
indicates a summation over all pairs of nearest-neighboring sites and the first summation is carried out only over nearest neighbour pairs of spins on different sublattices and J (J < 0) is the nearest-neighbour exchange parameter, DA is the crystal field interaction constant of spin-2 ions and DB is that of spin-3/2 ions. h is the external magnetic field acting on the lat tice.
In order to treat the model approximately we employ a variational method based on the Bogoliubov inequality for the Gibbs free energy which is given by the inequality,  , where
, where  is the true free energy of the model described by the Hamiltonian (1) and
is the true free energy of the model described by the Hamiltonian (1) and  is given by the relation
is given by the relation
 (2)
(2)
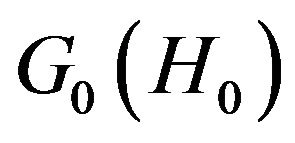 is the average free energy of a trial Hamiltonian
is the average free energy of a trial Hamiltonian  and
and 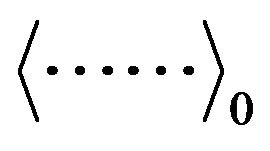 denotes a thermal average over the ensemble defined by
denotes a thermal average over the ensemble defined by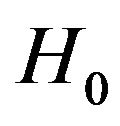 .
.
As the conventional procedure, the trial Hamiltonian is assumed to be in the form
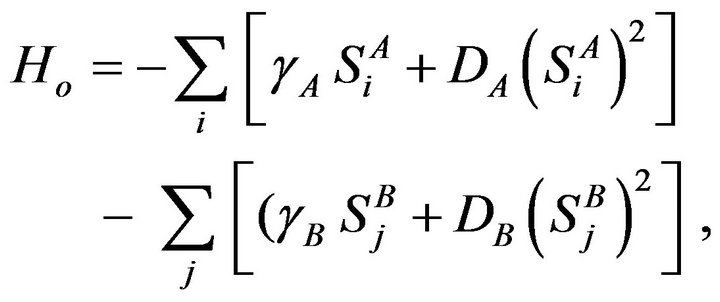 (3)
(3)
where  and
and  are the two variational parameters related to the molecular fields acting on the two different sublattices, respectively.
are the two variational parameters related to the molecular fields acting on the two different sublattices, respectively.
By evaluating Equation (2), it is easy to obtain the expression of the free energy per site in MFA
 (4)
(4)
where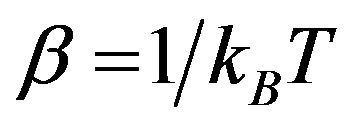 , N is the total number of sites of the lattice and z is the number of the nearest neighbors of every ion in the lattice. mA and mB are the sublattice magnetizations per site which are defined by Equations (5) and (6) below:
, N is the total number of sites of the lattice and z is the number of the nearest neighbors of every ion in the lattice. mA and mB are the sublattice magnetizations per site which are defined by Equations (5) and (6) below:
Now, by minimizing the free energy in Equation (4) with respect to 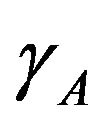 and
and , we obtain
, we obtain
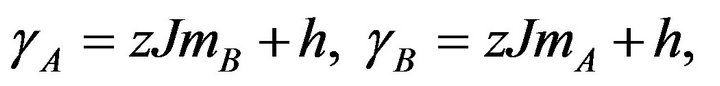 (7)
(7)
The mean field properties of the present system are then given by Equations (5)-(7). As the set of Equations (5)-(7) have in general several solutions for the pair, the
|
|
pair chosen is that which minimizes the free energy. given in Equation (5). We are here interested in studying the thermal variation of the sublattice magnetizations and the averaged total magnetization per site which defined as
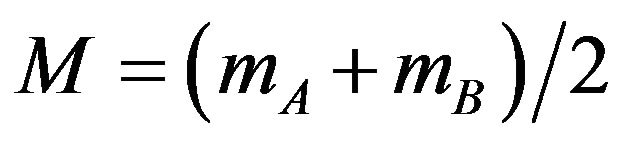 . (8)
. (8)
On the other hand, the sublattice initial susceptibilities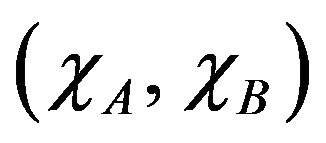 are defined by
are defined by
 .
.
From which the total initial susceptibility per site is given by
 . (9)
. (9)
3. Results and Discussions
3.1. Phase Diagrams
We begin with the ground-state structure of the system. At zero temperature, we find four phases with different values of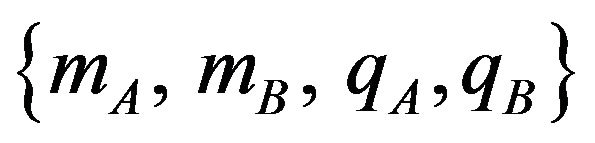 , namely the ordered ferrimagnetic phases
, namely the ordered ferrimagnetic phases
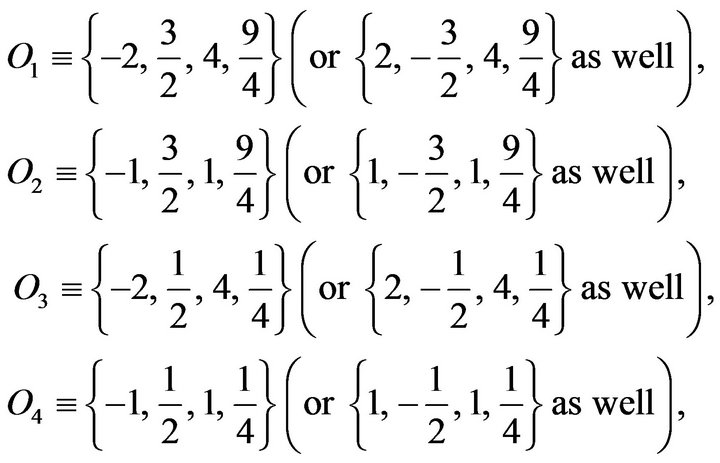
and disordered phases

where the parameters qA and qB are defined by:
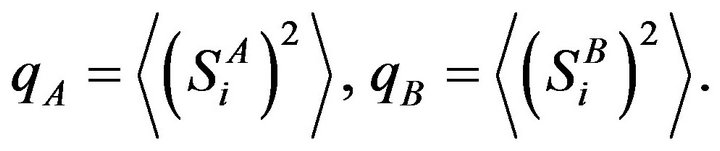
From Hamiltonian (1) and by comparing the groundstate energies of the different phases, the ground-state phase diagram can be determined, and is shown in Figure 1.
3.2. Sublattice Magnetizations mA and mB
In this subsection, let us at first examine the temperature dependence of the sublattice magnetizations mA and mB for the system. The results are depicted in Figure 2 with
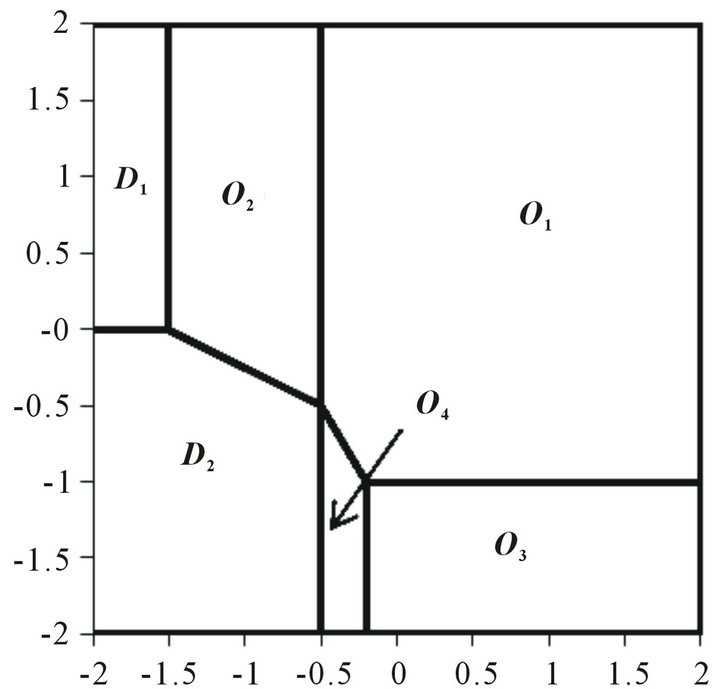
Figure 1. Ground-state phase diagram of the mixed spin-3/2 and spin-2 Ising ferrimagnetic system with the coordination number z and different single-ion anisotropies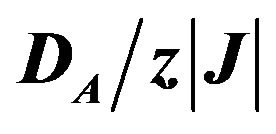 and
and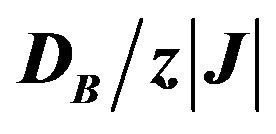 . The four phases: ordered O1, O2, O3, O4 and disordered D1, D2 are separated by first-order transition lines.
. The four phases: ordered O1, O2, O3, O4 and disordered D1, D2 are separated by first-order transition lines.

Figure 2. Thermal variation of the sublattice magnetizations mA, mB for the mixed-spin Ising ferrimagnet with the coordination number z, when the value of  is changed for fixed
is changed for fixed .
.
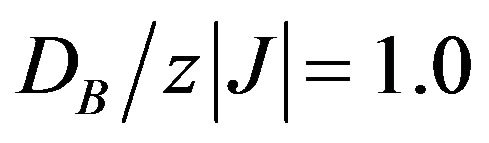 , and selected values of
, and selected values of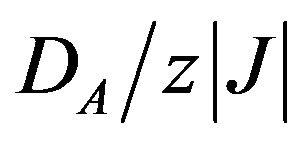 . Notice that the selection of
. Notice that the selection of 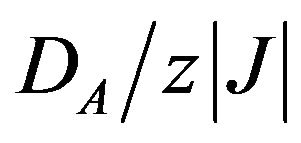 corresponds to the crossover from the O1 to the O2 phase (see the ground state phase diagram Figure 1), therefore the ground state is always ordered. When
corresponds to the crossover from the O1 to the O2 phase (see the ground state phase diagram Figure 1), therefore the ground state is always ordered. When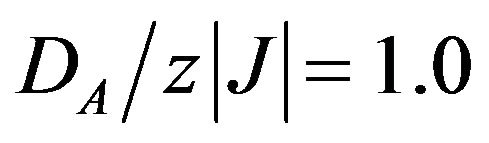 , the sublattice magnetizations mA and mB have standard characteristic convex shape. When
, the sublattice magnetizations mA and mB have standard characteristic convex shape. When 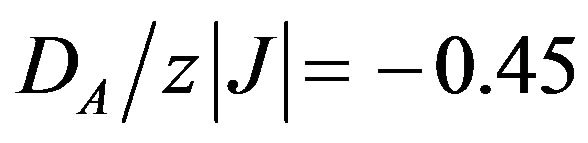 (slightly above the boundary between the phase O1 and the phase O3 in the ground state-phase diagram, where
(slightly above the boundary between the phase O1 and the phase O3 in the ground state-phase diagram, where ) the sublattice magnetization mA may exhibit a rather rapid decrease from its saturation value mA = 2.0 with the increase of temperature from T = 0 K to a certain temperature T. When
) the sublattice magnetization mA may exhibit a rather rapid decrease from its saturation value mA = 2.0 with the increase of temperature from T = 0 K to a certain temperature T. When  (at the boundary between the ordered phase O1 and the ordered phase O2 in the ground state phase-diagram), the saturation value of mA is 1.5, which indicates that the half of the spins on the sublattice A are equal to +2 (or −2 as well) and the other half are equal to +1 (or −1 as well). Note that this mixed state persists as long as
(at the boundary between the ordered phase O1 and the ordered phase O2 in the ground state phase-diagram), the saturation value of mA is 1.5, which indicates that the half of the spins on the sublattice A are equal to +2 (or −2 as well) and the other half are equal to +1 (or −1 as well). Note that this mixed state persists as long as 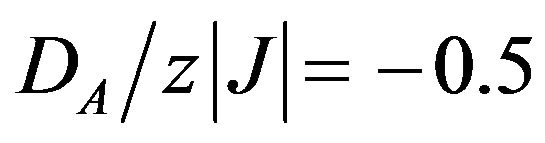 and
and . When
. When 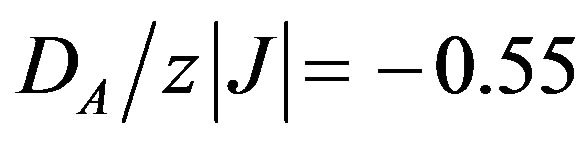 the ground state phase is O2 phase, with mA = 1.0 at T = 0 K. However, in this case the thermal variation of mA exhibits an interesting feature which is the initial rise of mA with the increase of temperature before decreasing to zero value at the critical point Tc.
the ground state phase is O2 phase, with mA = 1.0 at T = 0 K. However, in this case the thermal variation of mA exhibits an interesting feature which is the initial rise of mA with the increase of temperature before decreasing to zero value at the critical point Tc.
As shown in Figure 2, for 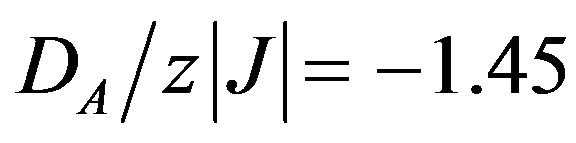 (slightly below the boundary between the ordered phase O2 and the disordered phase D1 in the ground state
(slightly below the boundary between the ordered phase O2 and the disordered phase D1 in the ground state ), the sublattice magnetization mA exhibits a rapid decrease before it decreases normally by increasing the value of
), the sublattice magnetization mA exhibits a rapid decrease before it decreases normally by increasing the value of 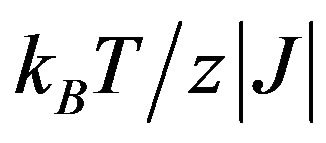 to the critical point Tc. In this case, a large magnetization jump is observed at the critical point, indicating a first-order transition. On the other hand, for all values of
to the critical point Tc. In this case, a large magnetization jump is observed at the critical point, indicating a first-order transition. On the other hand, for all values of 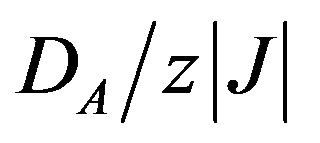 the sublattice magnetization mB decreases normally by increasing the value of
the sublattice magnetization mB decreases normally by increasing the value of 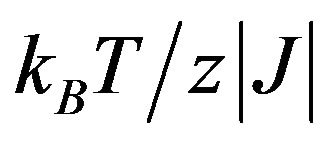 to the critical point Tc, even though it is coupled to mA. The previous results for sublattice magnetization are similar to those observed in the Mixed Spin-3/2 and Spin-2 Ising Ferrimagnetic System within the Effective- field Theory [30] and in the mixed-spin-1 and spin-3/2 Ising ferrimagnetic system [31-33].
to the critical point Tc, even though it is coupled to mA. The previous results for sublattice magnetization are similar to those observed in the Mixed Spin-3/2 and Spin-2 Ising Ferrimagnetic System within the Effective- field Theory [30] and in the mixed-spin-1 and spin-3/2 Ising ferrimagnetic system [31-33].
Figure 3 shows the sublattice magnetization curves as a function of temperature for several values of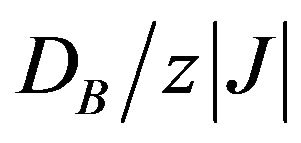 , when
, when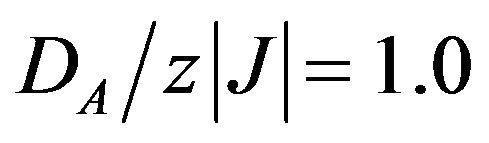 . In this case, the selection of
. In this case, the selection of 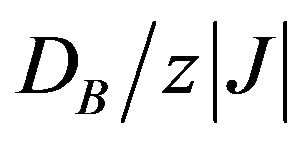 corresponds to the crossover from the O1 to the O3 phase. When
corresponds to the crossover from the O1 to the O3 phase. When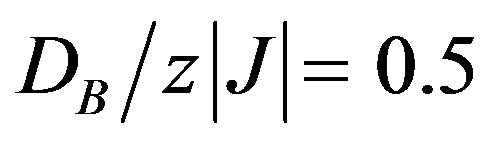 , the sublattice magnetization mA may show normal behaviour. When
, the sublattice magnetization mA may show normal behaviour. When 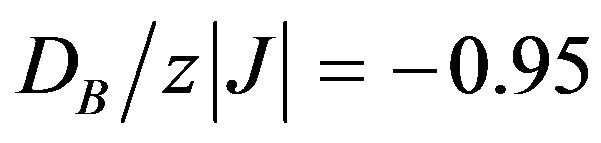 (slightly above the boundary between the ordered phase O1 and the ordered phase O2, where
(slightly above the boundary between the ordered phase O1 and the ordered phase O2, where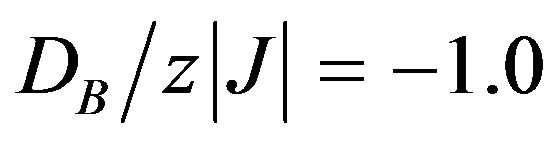 ) the magnetization curve mB may exhibit a rather rapid decrease from its saturation value (mB = −3/2) at T = 0 K, while for the value of
) the magnetization curve mB may exhibit a rather rapid decrease from its saturation value (mB = −3/2) at T = 0 K, while for the value of 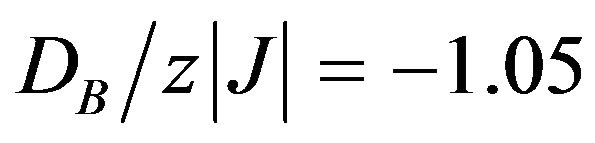 (slightly below that boundary), there is a rapid increase of mB from the saturation value (mB = −3/2) with the increase in T. When the value of
(slightly below that boundary), there is a rapid increase of mB from the saturation value (mB = −3/2) with the increase in T. When the value of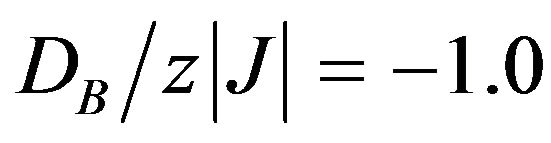 , the saturation value of the sublattice magnetization mB at T = 0 K is (mB = −1.0). It indicates that at this point, the spin configuration of
, the saturation value of the sublattice magnetization mB at T = 0 K is (mB = −1.0). It indicates that at this point, the spin configuration of  in the ground state consists of the mixed state; half of the spins on the sublattice B are equal to −3/2 (or +3/2 as well) and the other half are equal to −1/2 (or +1/2 as well). It is also seen from Figure 3 that when
in the ground state consists of the mixed state; half of the spins on the sublattice B are equal to −3/2 (or +3/2 as well) and the other half are equal to −1/2 (or +1/2 as well). It is also seen from Figure 3 that when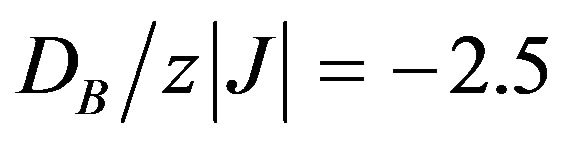 , the sublattice magnetization mB decreases normally from its saturation value (mB = −1/2) to vanish at the critical tem-
, the sublattice magnetization mB decreases normally from its saturation value (mB = −1/2) to vanish at the critical tem-
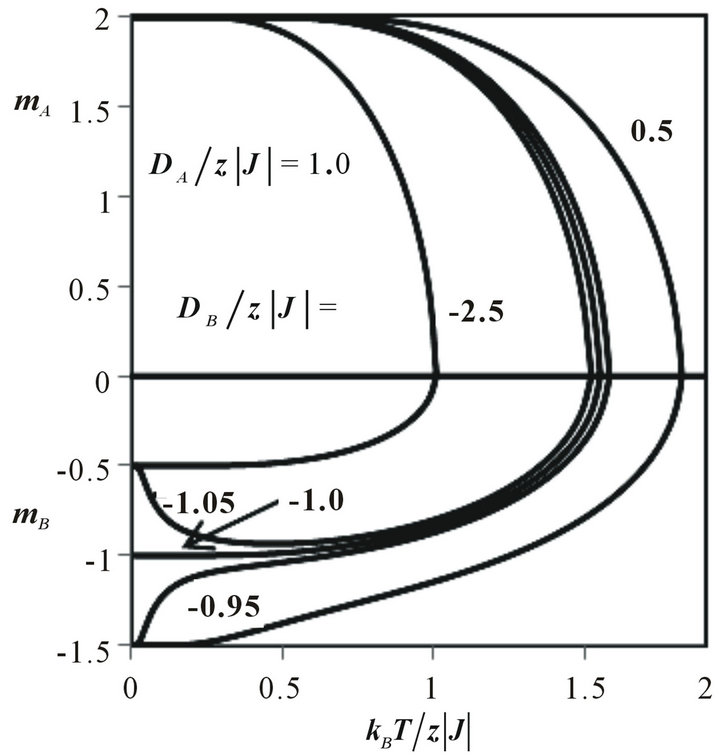
Figure 3. Thermal variation of the sublattice magnetizations mA, mB for the mixed-spin Ising ferrimagnet with the coordination number z, when the value of 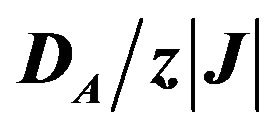 is changed for fixed
is changed for fixed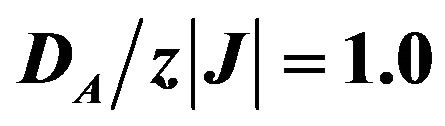 .
.
perature Tc.
On the other hand, for all the values of 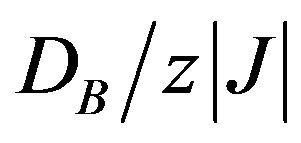 the sublattice magnetization mA may show normal behaviour, even though it is coupled to mB.
the sublattice magnetization mA may show normal behaviour, even though it is coupled to mB.
3.3. Susceptibility
In Figure 4, the temperature dependences of the initial susceptibilities (total and sublattices) of the system are shown for  and
and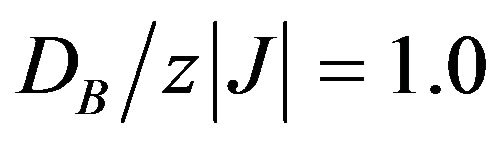 . We can see clearly that the total susceptibility
. We can see clearly that the total susceptibility  increases slowly by increasing temperature. When the temperature approaches Tc, the total susceptibility
increases slowly by increasing temperature. When the temperature approaches Tc, the total susceptibility increases very rapidly and goes to infinity at the critical temperature Tc. Moreover, one can observe that in the vicinity of Tc, the sublattice susceptibility
increases very rapidly and goes to infinity at the critical temperature Tc. Moreover, one can observe that in the vicinity of Tc, the sublattice susceptibility 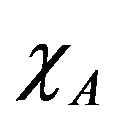 rapidly increases for
rapidly increases for 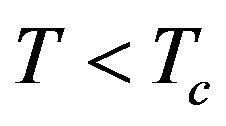 and goes to
and goes to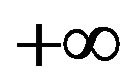 at
at 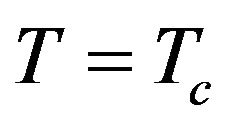 and rapidly decreases for
and rapidly decreases for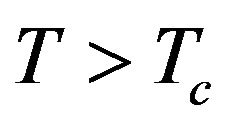 . On the other hand, the sublattice susceptibility
. On the other hand, the sublattice susceptibility 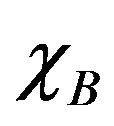 rapidly decreases for
rapidly decreases for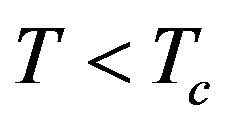 , goes to
, goes to 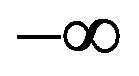 at
at  and rapidly increases for
and rapidly increases for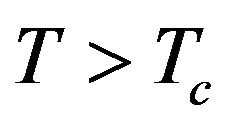 . In Figure 5, the total initial magnetic susceptibilities
. In Figure 5, the total initial magnetic susceptibilities are depicted for the system, with
are depicted for the system, with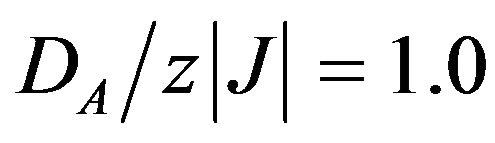 , when the value of
, when the value of 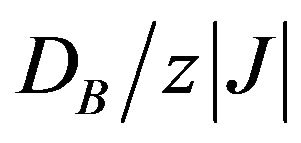 is changed. As is seen from this figure, the total susceptibility diverges at the critical temperature and the point of singularity shifts to lower temperature, upon decreasing the value of
is changed. As is seen from this figure, the total susceptibility diverges at the critical temperature and the point of singularity shifts to lower temperature, upon decreasing the value of . Now, besides the infinite values of
. Now, besides the infinite values of 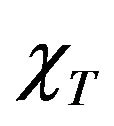 at,
at, 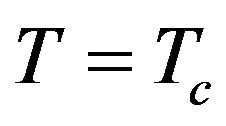 the total susceptibility at low temperatures exhibits a sharp maximum in the low-temperature region (when
the total susceptibility at low temperatures exhibits a sharp maximum in the low-temperature region (when 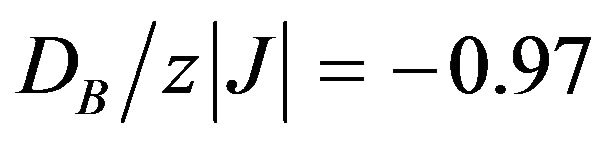 ) and a broad maximum (when
) and a broad maximum (when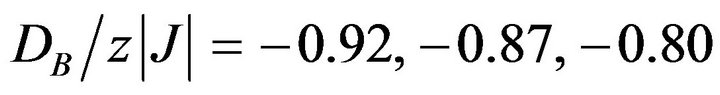 ). Particularly, It is seen from Figure 5 that the largest broad maximum appears
). Particularly, It is seen from Figure 5 that the largest broad maximum appears

Figure 4. Initial susceptibilities (total and sublattices) versus temperature for the mixed spin-3/2 and spin-2 Ising ferrimagnetic system with coordination number z, when 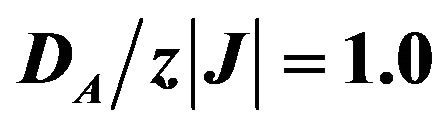 and
and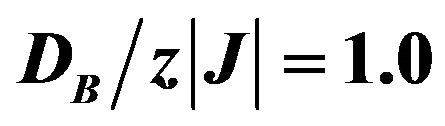 .
.

Figure 5. Thermal variations of the total initial susceptibility for the mixed spin-3/2 and spin-2 Ising ferrimagnetic system with the coordination number z, for several values of when the value of
when the value of .
.
for  and with the increase of
and with the increase of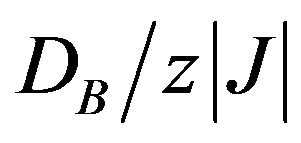 , its magnitude gradually decreases, and disappears when
, its magnitude gradually decreases, and disappears when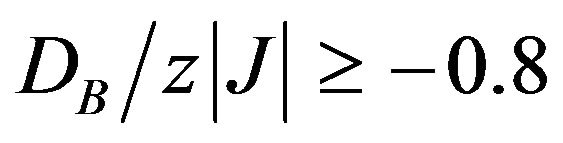 .
.
In Figure 6, temperature dependences of total and sublattice susceptibilities are presented for constant values of and
and . It is easy to see from this figure that the variation of the total susceptibility at low-temperature region originates from the behaviour of the
. It is easy to see from this figure that the variation of the total susceptibility at low-temperature region originates from the behaviour of the  sublattice susceptibility. It is also seen that the
sublattice susceptibility. It is also seen that the 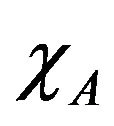 sublattice susceptibility exhibits the usual temperature dependence in the vicinity of Tc, while the sublattice susceptibility
sublattice susceptibility exhibits the usual temperature dependence in the vicinity of Tc, while the sublattice susceptibility  takes negative values. We notice that the existence of the sharp maxima (sharp peak) in the magnetic susceptibility was found by Na
takes negative values. We notice that the existence of the sharp maxima (sharp peak) in the magnetic susceptibility was found by Na
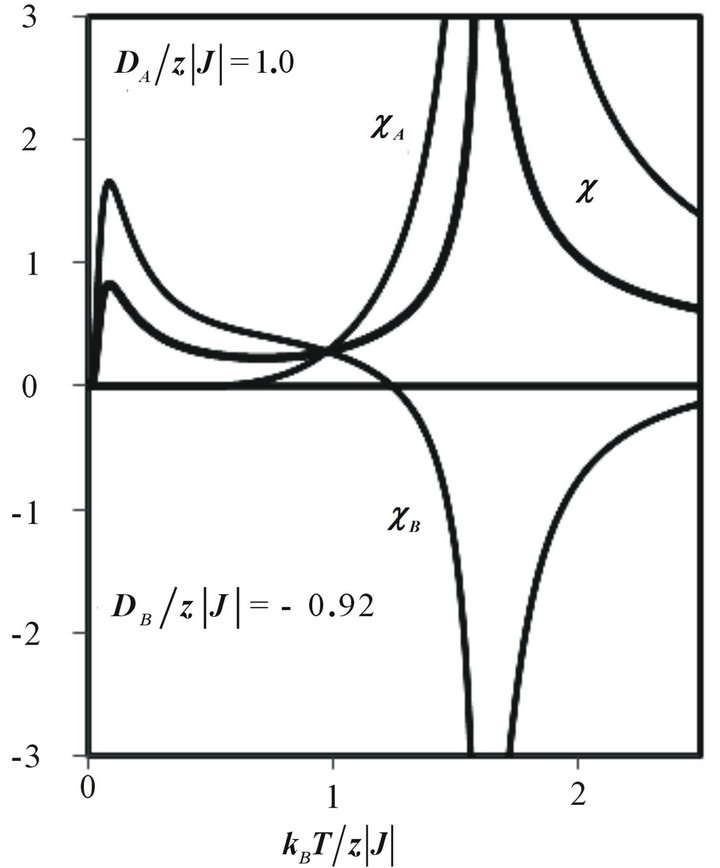
Figure 6. Initial susceptibilities (total and sublattices) versus temperature for the mixed spin-2 and spin-3/2 Ising ferrimagnet with coordination number z, when 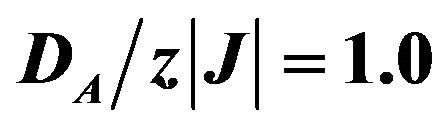 and
and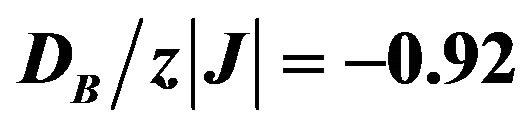 .
.
kamura and Tucker for the mixed spin-1 and spin-3/2 Ising ferrimagnet by using Monte Carlo simulation [34]. Moreover, the sharp and broad maxima can be observed in the mixed ferro-ferrimagnetic ternary alloy in reference [35].
In Figure 7, we present the temperature dependence of the total susceptibility for the system with 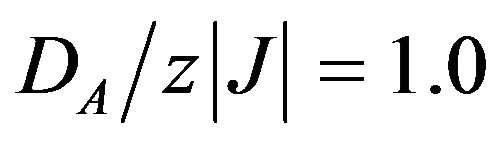 and
and 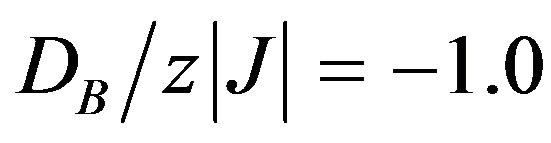 (in the boundary between the phase O1 and the phase O2, in the groundstate phase diagram (Figure 1)). In this case, the total susceptibility exhibits two divergences: one at T = 0 K indicating a first-order phase transition and another at
(in the boundary between the phase O1 and the phase O2, in the groundstate phase diagram (Figure 1)). In this case, the total susceptibility exhibits two divergences: one at T = 0 K indicating a first-order phase transition and another at , indicating a second-order phase transition. We notice that these effects can be observed for ferro-ferrimagnetic ternary alloy [35], site-diluted [36], bond-diluted [37], and site-bond-correlated Ising model [38].
, indicating a second-order phase transition. We notice that these effects can be observed for ferro-ferrimagnetic ternary alloy [35], site-diluted [36], bond-diluted [37], and site-bond-correlated Ising model [38].
In Figure 8, we show the thermal variation of the initial susceptibilities (total and sublattices). For the system with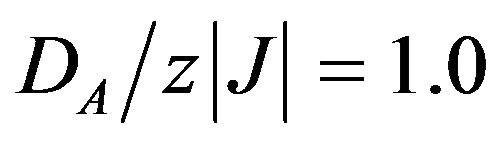 and
and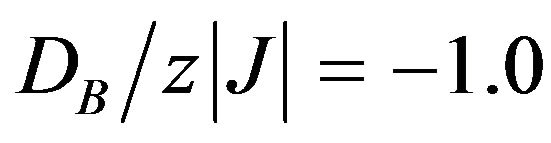 . It is seen from this figure that the divergence of the total susceptibility at zero temperature originates from the divergence of the sublattice susceptibility
. It is seen from this figure that the divergence of the total susceptibility at zero temperature originates from the divergence of the sublattice susceptibility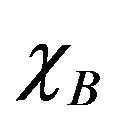 .
.
Now, in order to explain the appearance of the broad maximum in the susceptibility of the sublattice B in low-temperature region (Figure 6), we consider the temperature dependence of the sublattice magnetizations mA and mB (as shown in Figure 9) for the system with and
and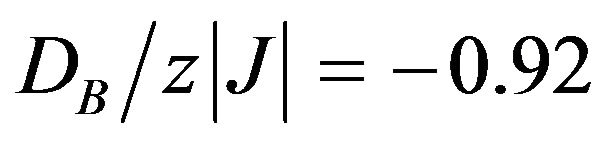 , when h = 0(solid lines) and when h ≠ 0 (dashed lines). In this figure, it is seen that there is a rapid decrease in mB from its saturation value (mB = −3/2) with the increase in T and it is clear that at any point of temperature in this region,
, when h = 0(solid lines) and when h ≠ 0 (dashed lines). In this figure, it is seen that there is a rapid decrease in mB from its saturation value (mB = −3/2) with the increase in T and it is clear that at any point of temperature in this region,
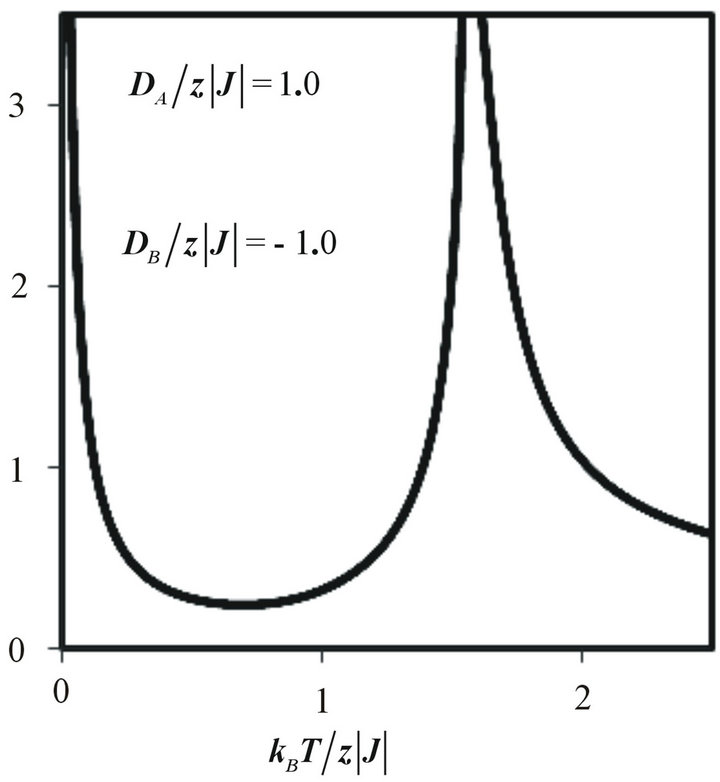
Figure 7. Thermal variations of the total initial susceptibility for the mixed spin-2 and spin-3/2 Ising ferrimagnet with the coordination number z, when the value of and the value of
and the value of .
.
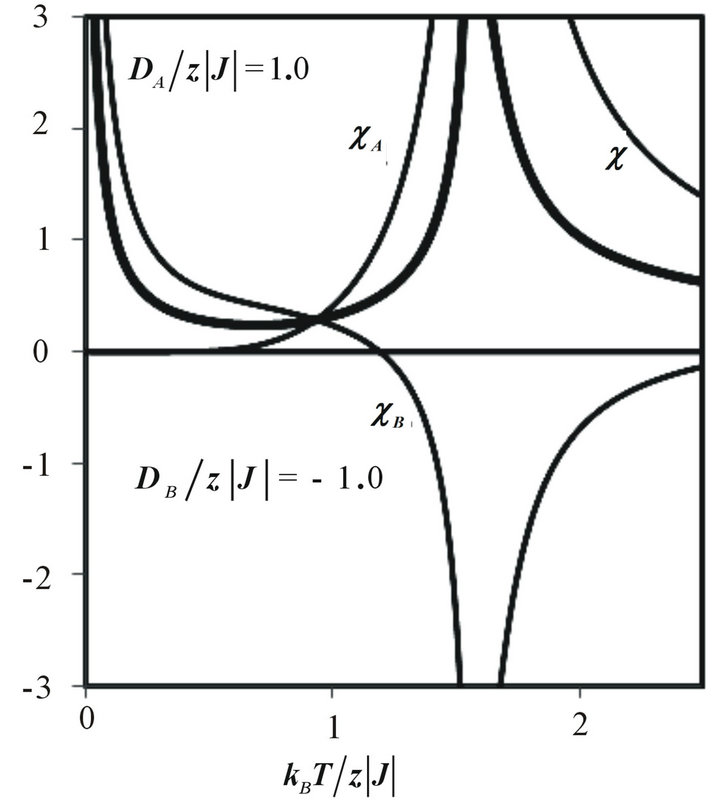
Figure 8. Initial susceptibilities (total and sublattices) versus temperature for the mixed spin-2 and spin-3/2 Ising ferrimagnet with coordination number z, when 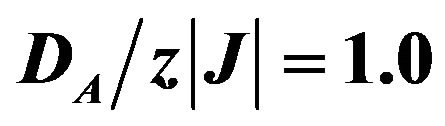 and
and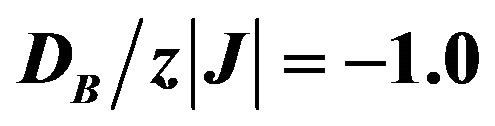 .
.
there is a jump in mB from a certain value, when h ≠ 0 to a lower value, when h = 0 resulting in the broad maximum of .
.
To explain the physical scenario for the appearance of the divergence of the susceptibility of the sublattice B at zero temperature (Figure 8), we consider the temperature dependence of the sublattice magnetizations mA and mB (as shown in Figure 10) for the system with  and
and , when h = 0 (solid lines) and when h ≠ 0 (dashed lines). In this figure, there is a mixed-spin state on the sublattice B in the ground state, for
, when h = 0 (solid lines) and when h ≠ 0 (dashed lines). In this figure, there is a mixed-spin state on the sublattice B in the ground state, for 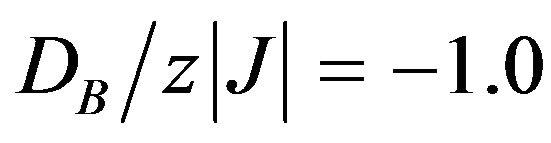 and h = 0, consisting from the
and h = 0, consisting from the  and
and 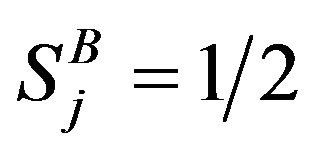 with equal probabilities.
with equal probabilities.

Figure 9. Thermal variation of the sublattice magnetizations mA, mB for the mixed-spin Ising ferrimagnet with the coordination number z. when the value of 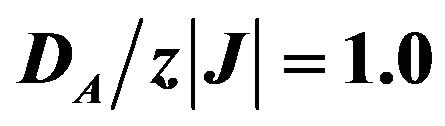 and
and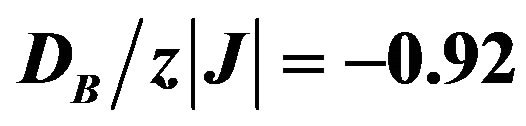 . The solid lines represent the sublattice magnetizations without an external magnetic field effect on the system (h = 0.0), while the dashed lines represent the sublattice magnetizations under the effect of an external magnetic field (h = 0.05).
. The solid lines represent the sublattice magnetizations without an external magnetic field effect on the system (h = 0.0), while the dashed lines represent the sublattice magnetizations under the effect of an external magnetic field (h = 0.05).

Figure 10. Thermal variation of the sublattice magnetizations mA, mB for the mixed-spin Ising ferrimagnet with the coordination number z. when the value of  and
and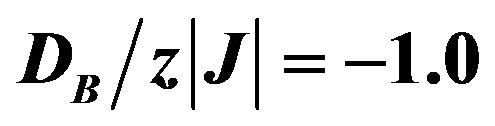 . The solid lines represent the sublattice magnetizations without an external magnetic field effect on the system (h = 0.0), while the dashed lines represent the sublattice magnetizations under the effect of an external magnetic field (h = 0.05).
. The solid lines represent the sublattice magnetizations without an external magnetic field effect on the system (h = 0.0), while the dashed lines represent the sublattice magnetizations under the effect of an external magnetic field (h = 0.05).
However, at h ≠ 0 the 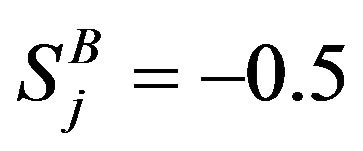 is suddenly favored resulting in a divergence of the
is suddenly favored resulting in a divergence of the 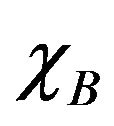 sublattice susceptibility at T = 0 K.
sublattice susceptibility at T = 0 K.
4. Conclusions
In this paper, we have studied the magnetic properties of a ferrimagnetic mixed spin-3/2 and spin-2 Ising system with different single ion anisotropies in a longitudinal magnetic field by using the meanfield theory based on Bogoliubov inequality for the Gibbs free energy.
The ground state phase diagram of the model was constructed in 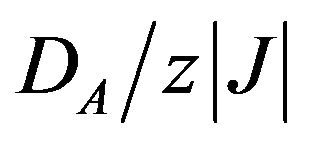 and
and 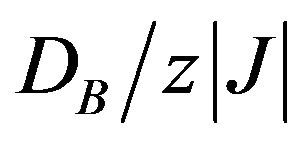 plane. In this phase diagram, we have found four ordered phases and two disordered phases separated by first order lines. We also have investigated the thermal variations of the sublattice magnetizations for selected values of
plane. In this phase diagram, we have found four ordered phases and two disordered phases separated by first order lines. We also have investigated the thermal variations of the sublattice magnetizations for selected values of 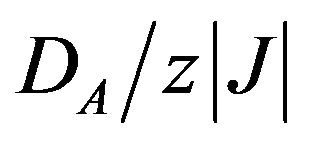 and
and 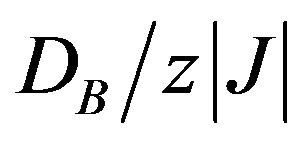 and we have found some interesting results in the sublattice magnetization curves we have found that the sublattice magnetizations may exhibit a rather rapid decrease from their saturation values with the increase of temperature from T = 0 K to a certain temperature T. The initial susceptibilities (total and sublattices) of the system are considered for selected values of
and we have found some interesting results in the sublattice magnetization curves we have found that the sublattice magnetizations may exhibit a rather rapid decrease from their saturation values with the increase of temperature from T = 0 K to a certain temperature T. The initial susceptibilities (total and sublattices) of the system are considered for selected values of 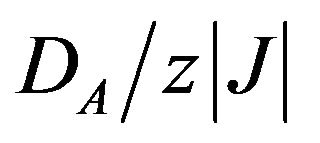 and
and  and The temperature dependences of the initial susceptibilities (total and sublattices) of the system are considered for selected values of
and The temperature dependences of the initial susceptibilities (total and sublattices) of the system are considered for selected values of 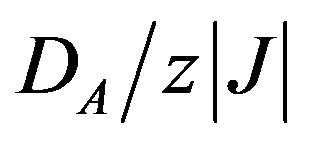 and
and 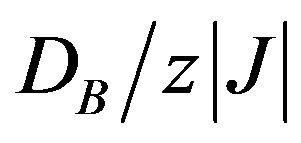 and we have found that besides the infinite values of
and we have found that besides the infinite values of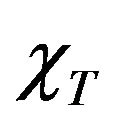 at
at 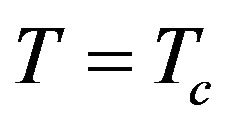 the total susceptibility at low temperatures may exhibits a sharp maximum or broad maximum in the low-temperature region (when
the total susceptibility at low temperatures may exhibits a sharp maximum or broad maximum in the low-temperature region (when 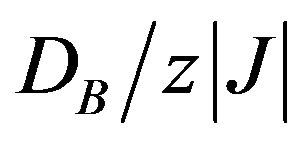 approaches the boundary between the phases in the ground state phase diagram). We have also found that the susceptibility (in the boundary between the phases in the ground state phase diagram) may exhibit two divergences: one at T = 0 K indicating a first-order phase transition and another at
approaches the boundary between the phases in the ground state phase diagram). We have also found that the susceptibility (in the boundary between the phases in the ground state phase diagram) may exhibit two divergences: one at T = 0 K indicating a first-order phase transition and another at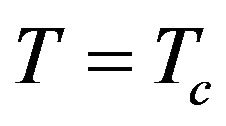 , indicating a second-order phase transition.
, indicating a second-order phase transition.
REFERENCES
- O. Khan, “Molecular Magnetism,” VCH Publishers, New York, 1993.
- T. Kaneyoshi and Y. Nakamura, “A Theoretical Investigation for Low-Dimensional Molecular-based Magnetic Materials,” Journal of Physics: Condensed Matter, Vol. 10, No. 13, 1998, p. 3003. doi:10.1088/0953-8984/10/13/017
- T. Kaneyoshi, Y. Nakamura and S. Shin, “A Diluted Mixed Spin-2 and Spin-5/2 Ferrimagnetic Ising System; a Study of a Molecular-Based Magnet,” Journal of Physics, Condensed Matter, Vol. 10, No. 31, 1998, p. 7025. doi:10.1088/0953-8984/10/31/018
- M. Mansuripur, “Magnetization Reversal, Coercivity, and the Process of Thermomagnetic Recording in Thin Films of Amorphous Rare Earth Transition Metal Alloys,” Journal of Applied Physics, Vol. 61, No. 4, 1987, pp. 1580-1587. doi:10.1063/1.338094
- F. Tanaka, S. Tanaka and N. Imamura, “Magneto-Optical Recording Characteristics of TbFeCo Media by Magnetic Field Modulation Method,” Japan Journal of Applied Physics, Vol. 26, 1987, pp. 231-235. doi:10.1143/JJAP.26.231
- L. L. Goncaloves, ‘‘Uniaxial Anisotropy Effects in the Ising Model: An Exactly Soluble Model,” Physica Scripta, Vol. 32, No. 3, 1985, p. 248. doi:10.1088/0031-8949/32/3/012
- L. L. Goncaloves, “Uniaxial Anisotropy Effects in the Ising Model: An Exactly Soluble Model,” Physica Scripta, Vol. 33, No. 2, 1986, p. 192. doi:10.1088/0031-8949/33/2/018
- A. Dakhama and N. Benayad, “On the Existence of Compensation Temperature in 2d Mixed-Spin Ising Ferrimagnets: An Exactly Solvable Model,” Journal of Magnetism and Magnetic Materials, Vol. 213, No. 1-2, 2000, pp. 117-125. doi:10.1016/S0304-8853(99)00606-X
- N. R. da Silva and S. R. Salinas, “Mixed-Spin Ising Model on Beth Lattice,” Physical Review, Vol. 44, No. 2, 1991, pp. 852-855. doi:10.1103/PhysRevB.44.852
- J. W. Tucker, “The Ferrimagnetic Mixed Spin-1/2 and Spin-1 Sing System,” Journal of Magnetism and Magnetic Materials, Vol. 195, No. 3, 1999, pp. 733-740. doi:10.1016/S0304-8853(99)00302-9
- T. Kaneyoshi and J. C. Chen, “Mean-Field Analysis of a Ferrimagnetic Mixed Spin System,” Journal of Magnetism and Magnetic Materials, Vol. 98, No. 1-2, 1991, pp. 201-204. doi:10.1016/0304-8853(91)90444-F
- T. Kaneyoshi, “Curie Temperatures and Tricritical Points in Mixed Ising Ferromagnetic Systems,” The Physical Society of Japan, Vol. 56, 1987, pp. 2675-2680. doi:10.1143/JPSJ.56.2675
- T. Kaneyoshi, “Phase Transition of the Mixed Spin System with a Random Crystal Field,” Physica A, Vol. 153, No. 3, 1988, pp. 556-566. doi:10.1016/0378-4371(88)90240-3
- T. Kaneyoshi, M. Jascur and P. Tomczak, “The Ferrimagnetic Mixed Spin-1/2 and Spin-3/2 Ising System,” Journal of Physics: Condensed Matter, Vol. 4, No. 49, 1992, pp. L653-L658. doi:10.1088/0953-8984/4/49/002
- T. Kaneyoshi, “Tricritical Behavior of a Mixed Spin-1/2 and Spin-2 Ising System,” Physica A, Vol. 205, No. 4, 1994, pp. 677-686. doi:10.1016/0378-4371(94)90229-1
- A. Bobak and M. Jurcisin, “Discussion of Critical Behaviour in a Mixed-Spin Ising Model,” Physica A, Vol. 240, No. 3-4, 1997, pp. 647-656. doi:10.1016/S0378-4371(97)00044-7
- S. G. A. Quadros and S. R. Salinas, “RenormalizationGroup Calculations for a Mixed-Spin Ising Model,” Physica A: Statistical Mechanics and Its Applications, Vol. 206, No. 3-4, 1994, pp. 479-496.
- G.-M. Zhang and C.-Z. Yang, “Monte Carlo Study of the Two-Dimensional Quadratic Ising Ferromagnet with Spins S=1/2 and S=1 and with Crystal-Field Interactions,” Physical Review B, Vol. 48, No. 13, 1993, pp. 9452-9455. doi:10.1103/PhysRevB.48.9452
- G. M. Buendia and M. A. Novotny, “Numerical Study of a Mixed Ising Ferrimagnetic System,” Journal of Physics: Condensed Matter, Vol. 9, No. 27, 1997, pp. 5951-5964. doi:10.1088/0953-8984/9/27/021
- G. M. Buendia and J. A. Liendo, “Monte Carlo Simulation of a Mixed Spin-1/2 and Spin-3/2 Ising Ferrimagnetic System,” Journal of Physics: Condensed Matter, Vol. 9, No. 25, 1997, pp. 5439-5448. doi:10.1088/0953-8984/9/25/011
- M. Doerr, S. Kramp, M. Loewenhaupt, M. Rotter, R. Kratz, H. Krug, D. Eckert, H. Siegel and P. Verges, “Anomalous Magnetic Behaviour of NdCu2 in High Magnetic Fields,” Physica B: Condensed Matter, Vol. 294- 295, 2001, pp. 164-167. doi:10.1016/S0921-4526(00)00633-5
- K. Koyama, H. Fujii, T. Goto, H. Fukuda and Y. Janssen, “Magnetic Phase Transitions of Ce2Fe17 under High Pressures and High Magnetic Fields,” Physica B: Condensed Matter, Vol. 294-295, 2001, pp. 168-171. doi:10.1016/S0921-4526(00)00634-7
- F. Albertini, F. Bolzoni, A. Paoluzi, L. Pareti and E. Zannoni, “Magnetic-Field Induced First-Order Transitions in the Intermetallic Compound Pr2Fe17,” Condensed Matter, Vol. 294-295, 2001, pp. 172-176. doi:10.1016/S0921-4526(00)00635-9
- C. Ekiz and M. Keskin, “Magnetic Properties Of The Mixed Spin-1/2 and Spin-1 Ising Ferromagnetic System,” Physica A, Vol. 317, No. 3-4, 2003, pp. 517-534. doi:10.1016/S0378-4371(02)01356-0
- G.-Z. Wei, Y.-Q. Liang, Q. Zhang and Z.-H. Xin, “Magnetic Properties of Mixed-Spin Ising Systems in a Longitudinal Magnetic Field,” Journal of Magnetism and Magnetic Materials, Vol. 271, No. 2-3, 2004, pp. 246-253. doi:10.1016/j.jmmm.2003.09.043
- C. Ekiz, “Mixed Spin-1/2 and Spin-3/2 Ising System in a Longitudinal Magnetic Field,” Journal of Magnetism and Magnetic Materials, Vol. 293, No. 3, 2005, pp. 913-923. doi:10.1016/j.jmmm.2004.12.012
- M. Aouzi, M. El Hafidi and E. M. Sakhaf, “Thermodynamic and Magnetic Properties of a Mixed Ising System on a Triangular Array in Presence of Longitudinal Field,” Physica A, Vol. 345, No. 3-4, 2005, pp. 575-590.
- W. Jiang and B.-D. Bai, “Hysteresis Loops and Susceptibility of Ferromagnetic or Ferrimagnetic Bilayer System,” Physica Status Solidi (b), Vol. 243, No. 12, 2006, pp. 2892-2900. doi:10.1002/pssb.200541244
- B. Deviren, M. Keskinb and O. Cankob, “Magnetic Properties of an Anti-Ferromagnetic and Ferrimagnetic Mixed Spin-1/2 and Spin-5/2 Ising Model in the Longitudinal Magnetic Field within the Effective-Field Approximation,” Physica A, Vol. 388, No. 9, 2009, pp. 1835-1848. doi:10.1016/j.physa.2009.01.032
- B. Deviren, E. Kantar and M. Keskin, “Magnetic Properties of a Mixed Spin-3/2 and Spin-2 Ising Ferrimagnetic System within the Effective-Field Theory,” Journal of the Korean Physical Society, Vol. 56, No. 6, 2010, pp. 1738- 1747. doi:10.3938/jkps.56.1738
- O. F. Abubrig, D. Horvath, A. Bobak and M. Jascur, “Mean-Field Solution of the Mixed Spin-1 and Spin-3/2 Ising System with Different Single-Ion Anisotropies,” Physica A, Vol. 296, No. 3-4, 2001, pp. 437-450.
- A. Bobak, O. F. Abubrig and D. Horvath, “An Effective-Field Study of the Mixed Spin-1 and Spin-3/2 Ising Ferrimagnetic System,” Journal of Magnetism and Magnetic Materials, Vol. 246, No. 1-2, 2002, pp. 177-183. doi:10.1016/S0304-8853(02)00048-3
- C. Ekiz, “The Possibility of Two Compensation Points in a Ferrimagnetic Mixed Spin-1 and Spin-3/2 Ising System Using Bethe Lattice Approach,” Journal of Magnetism and Magnetic Materials, Vol. 307, No. 1, 2006, pp. 139- 147. doi:10.1016/j.jmmm.2006.03.059
- Y. Nakamura and J. W. Tucker, “Monte Carlo Study of a Mixed Spin-1 and Spin-3/2 Ising Ferromagnet,” IEEE Transactions on Magnetics, Vol. 38, No. 5, 2002, pp. 2406-2408. doi:10.1109/TMAG.2002.803598
- A. Bobak, O. F. Abubrig and D. Horvath, “Magnetic Properties of a Mixed Ferro-Ferrimagnetic Ternary Alloy,” Physica A, Vol. 312, No. 1-2, 2002, pp. 187-207. doi:10.1016/S0378-4371(02)00864-6
- T. Kaneyoshi, I. Tamura and R. Honmura, “Dilute Ising Ferromagnet: Its Physical Proprties,” Physical Review B, Vol. 29, No. 5, 1984, pp. 2769-2776. doi:10.1103/PhysRevB.29.2769
- A. Bobak and M. Jascur, “Correlated Effective-Field Theory of the Site-Diluted Ising Model,” Journal of Magnetism and Magnetic Materials, Vol. 136, No. 1-2. 1994, pp. 105-117. doi:10.1016/0304-8853(94)90454-5
- A. A. da Silva and F. G. Brady Moreira, “Thermodynamic Properties and Phase Transitions of the Site-BondCorrelated Ising Model,” Physical Review B, Vol. 40, No. 16, 1989, pp. 10986-10991. doi:10.1103/PhysRevB.40.10986