ABSTRACT

The dissipative part of the linear magnetic dynamic susceptibility of dipolar spin glasses is considered. Due to the transition of the system (at enough high concentration of the magnetic dipoles) from a paramagnetic phase to magnetic dipolar one, an anomalous temperature dependence of the dissipative part of the magnetic susceptibility is found. Our results are in qualitative agreement with experiments performed on the dipolar-coupled Ising magnet LiHo_xY_1-xF₄.

1. Introduction

Dipolar interactions are always present in paramagnets and paraelectrics systems. During the last years, dilute magnetic dipolar systems have been the subject of many studies addressing, in particular, the question of whether or not a spin glass like phase exists in these systems [1-7]. Examples include disordered magnetic materials, diluted ferromagnetic materials [7]. The dipole-dipole interaction have a similar behaviour of the RKKY interaction that fall off as 1/r³ so, one might expect the existence of a spin glass phase transition with a low freezing temperature. The most studied example of such models is the dilute, insulating, dipolar-coupled Ising magnetic LiHo_xY_1-xF₄ (non magnetic Y for magnetic Ho) which presents a freezing temperature Tg = 0.13 K for x = 0.167 [3].

The model hamiltonian has the form:

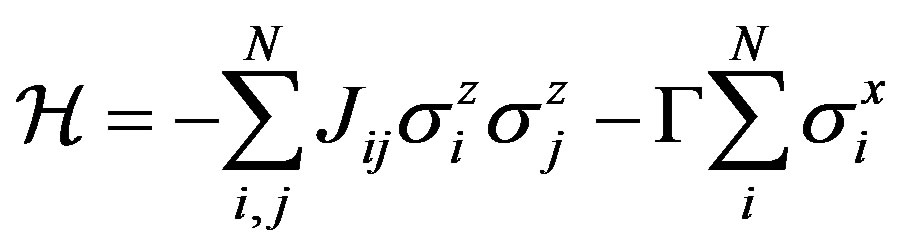
where the J_ij are random longitudinal dipole-dipole couplings, Γ is the transverse field and the’s are Pauli spin matrices. Due to the long range nature of the dipoledipole interaction many interesting and non trivial low-temperatures properties are expected. Recently, the possibility of a spin glass phase transition in a randomly dilute classical Ising dipoles has been questioned on the basis of a Wang-Landau Monte Carlo simulation [5] and experiments employing a µSQUID magnetometer [6]. The results obtained lead the authors to the conclusion that LiHo_0.167Y_0.833F₄ is not a spin glass. On the contrarya very recent experimental paper [7] prove the existence of a spin glass transition for x = 0.167 and 0.198. The problem remain open. Finally we note that the some kind of questions arise when we investigate dipolar pseudo spin glasses model with electric impurity dipolar centers in crystals or the role of the strong interactions between the elastic tunneling defects like the two-level system (TLS) in glass [8-14]. In this paper the magnetic dynamical susceptibility of dipolar spin glass in a transverse field is theoretically considered. The main result is an anomalous temperature dependence of the dissipative part of the magnetic susceptibility due to the transition of the system from paramagnetic phase to magnetic dipolar glass one.

2. The Model Hamiltonian

Let us consider an ensemble of the interacting, between each other, magnetic dipoles distributed homogeneously and randomly over lattice sites. We consider the dominant magnetic interaction as dipolar and strong interaction between magnetic dipoles and lattice vibrations. The hamiltonian of the N two-level magnetic dipolar impurities in the crystal is:

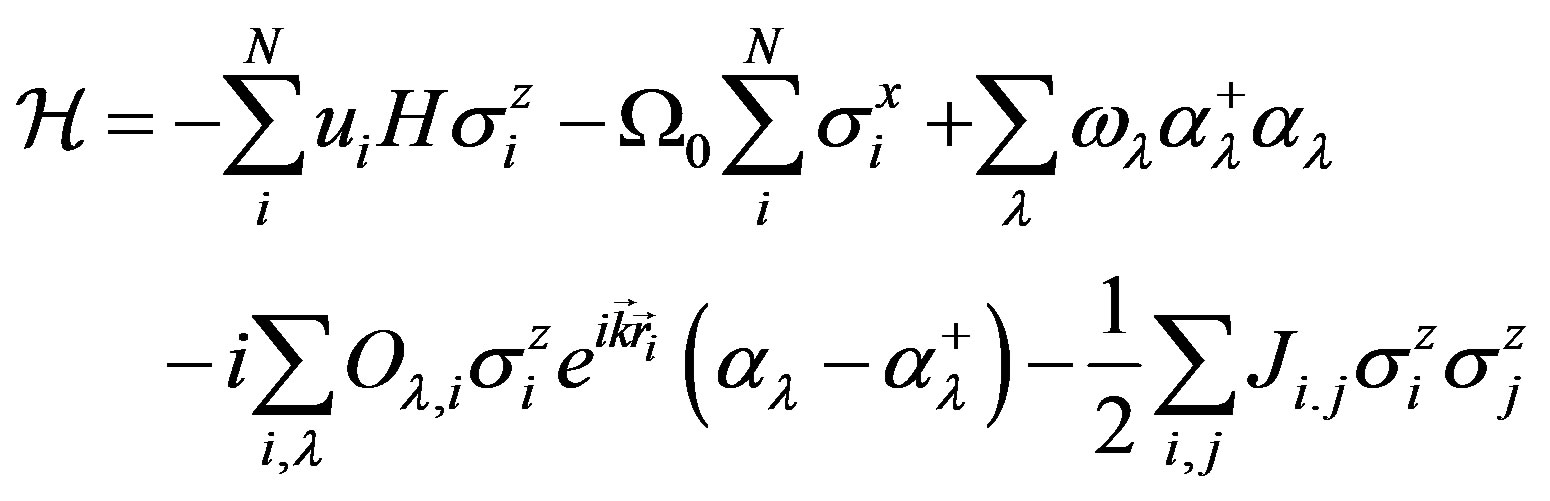(1)

In Equation (1), 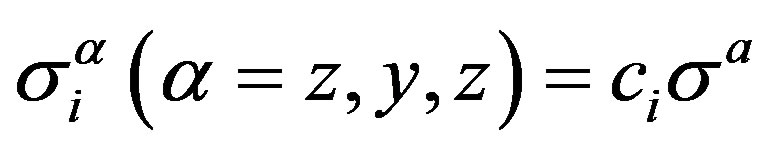with c_i = 1 if the site is occupied by dipole, c_i = 0 if not. σ^a are the Pauli spin operators. Index λ covers branch of phonon spectrum and wave vector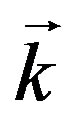. The first term in Equation (1) describes the dipole interaction with an external dc magnetic field H, μ is the value of the magnetic dipole moment, μ = gμB (g is the Landè factor, μB is the magneton of Bohr). The second term represents the tunneling of the dipole, Ω₀ is the nonrenormalized tunneling parameter. The third term describes the lattice vibrations, ω_λ is the phonon frequency and 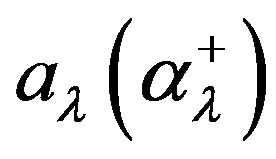are the phononannihilation (creation) operators. Finally, the fourth and fifth terms represents dipole-lattice and dipole-dipole interaction with coupling constants O_λi and 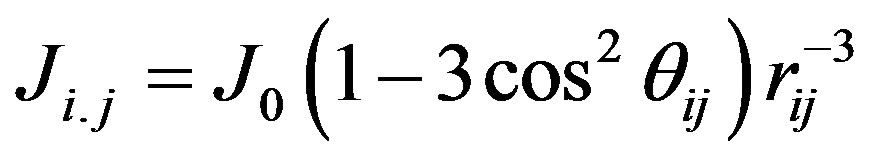, respectively. Note the longrange character of ~ 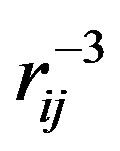where r_ij is the interspin distance, 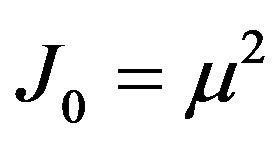and θ_λi is the angle formed by the Ising axis and the vector connecting the spin. The angular dependence of J_i,j means that it can change sign. The spin-phonon interaction is regulated by some mechanism [15,16]. In magnetic substances the main role is played by the modulation of the exchange interaction due to lattice vibrations. These latter may also give modulation of magnetic field produced on a given spin due to the surrounding spins. This is the Valler’s mechanism namely, the modulation of the dipolar spin-spin interaction due to lattice vibrations. This represents the mechanism relevant for us. For paramagnetic systems becomes relevant the Van-Fleck’s mechanism, i.e. the modulation, due to lattice vibration of the crystal electric field on spin site. Sented by an interaction of the dipolar magnetic system with an ac magnetic external field. It is written as:

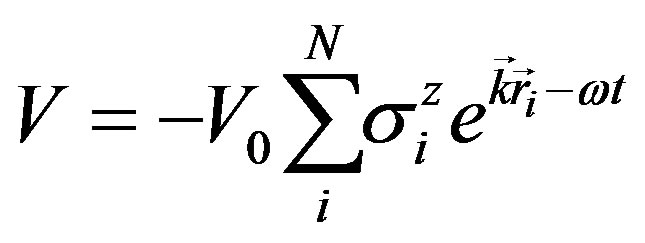(2)

where V₀ = μh, h is the amplitude of the ac magnetic field with momentum 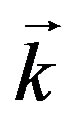and angular frequency ω. To take into account the fourth term in (1) exactly, one must perform a canonical unitary transformation of hamiltonian (1) of the form:

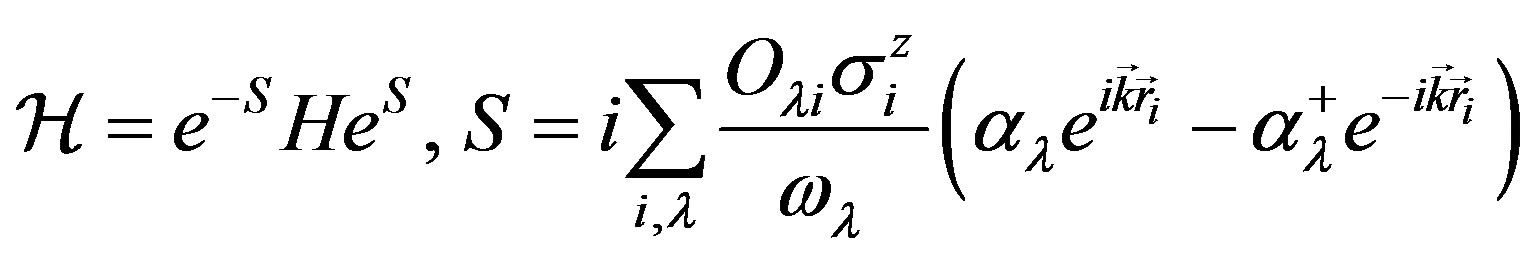(3)

In this way the term with the dipole lattice coupling disappears. After the transformation (3) we get instead of (1) the following Hamiltonian,

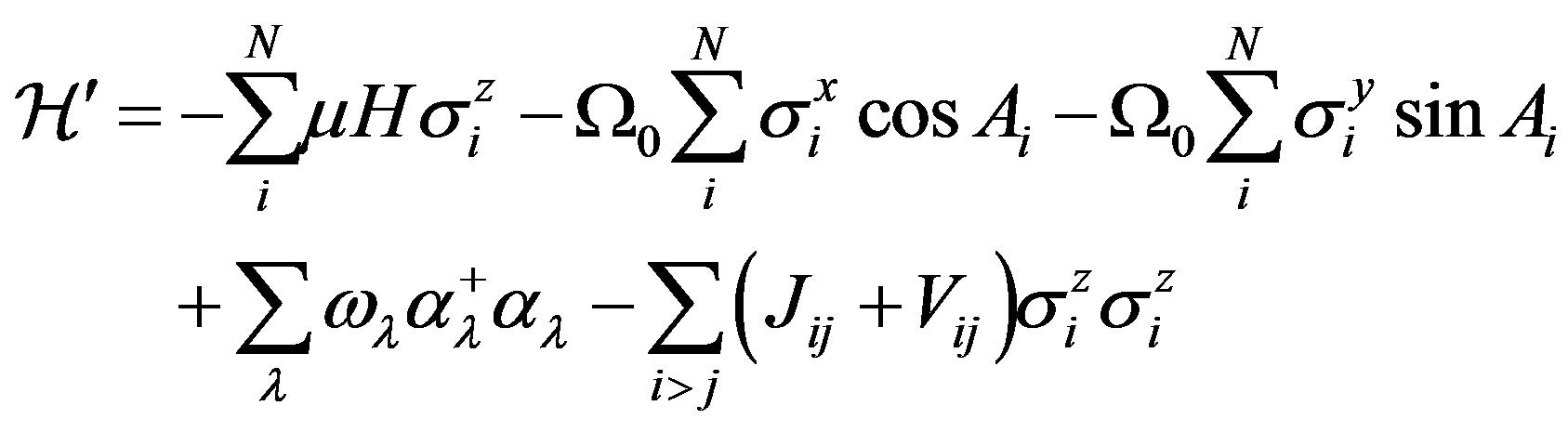(4)

where,

with

V_ij represents the indirect (through the phonon field) interaction between dipole impurities. Diagonalizing the linear (over 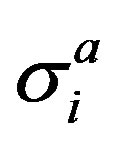operators) part of the hamiltonian 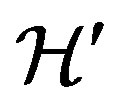by transformation to the new operators [8-11],

(5)

we obtain the system hamiltonian of the form,

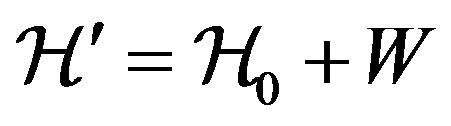
with,

(6)

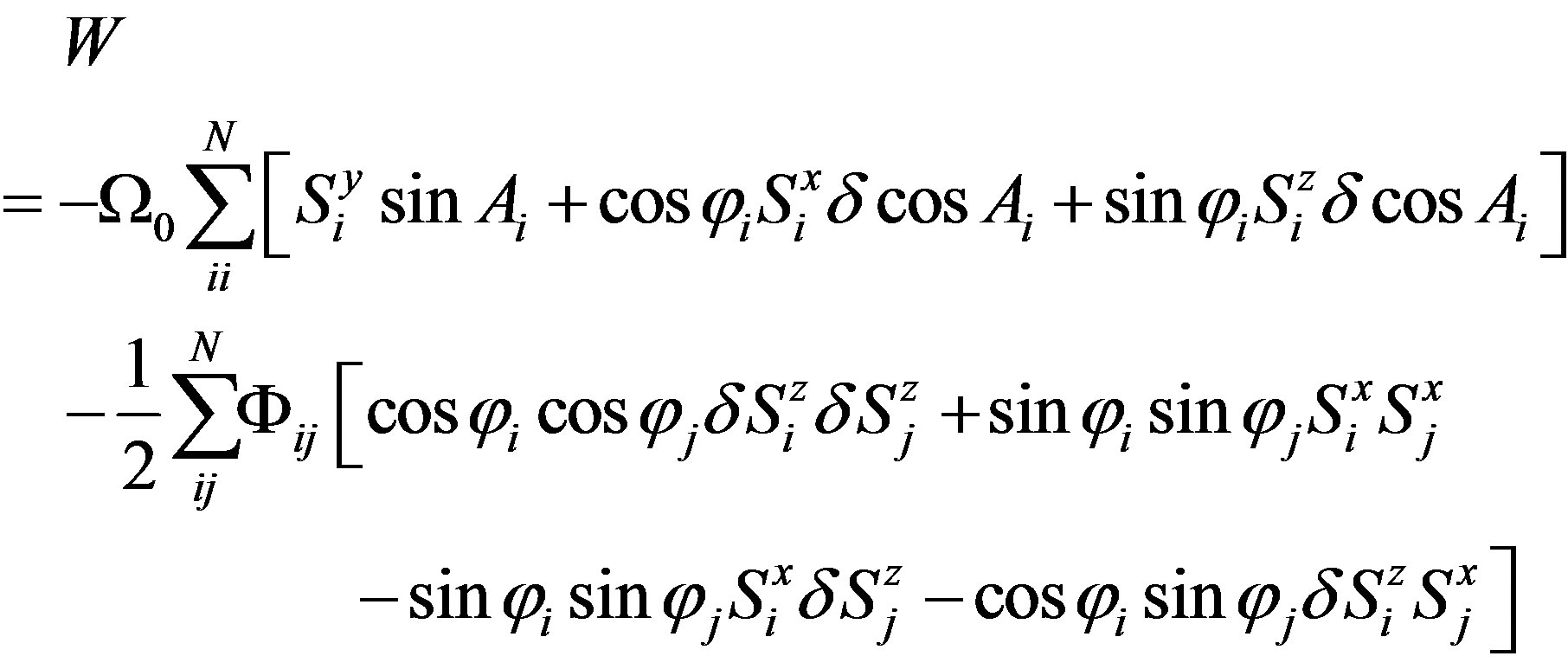(7)

with 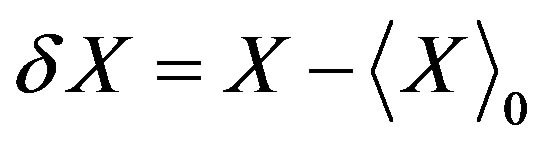where means the thermal average with the Hamiltonian.

In Equation (5), 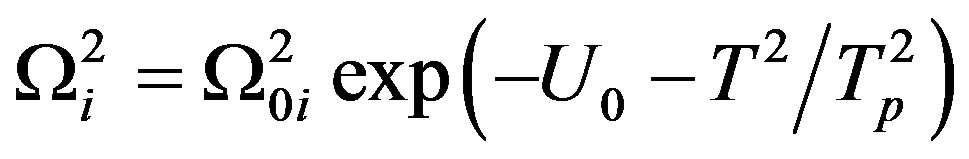is the (strong dipole-dipole coupling) tunneling parameter, 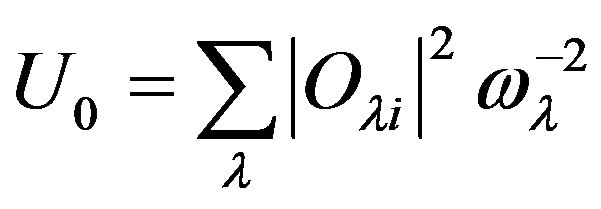, T_p is the characteristic temperature above which the multiphonon relaxation process becomes important [17] and 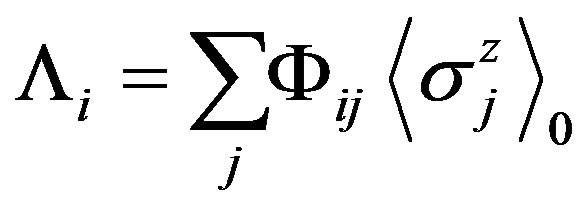represents the internal “molecular” random field which is due to other j^th dipoles and it is a random function of the site i. Here we consider only z-component of this field. The distribution function 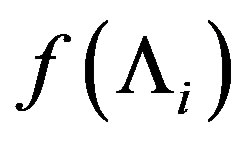of random mean fields Λ_i was considered in papers [8,9,18]. We note that the introduction of the random field Λ_i with some distribution function 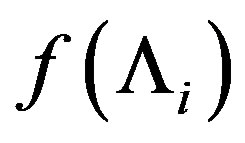allows the many-particle problem to lead to one particle unperturbed random hamiltonian and the perturbation W. For random system like spin glass the equivalence of the configurational average to the average over random molecular fields with distribution function, is usually used [8,9,18]. Klein et al. [18] consider a self-consistent mean random field approximation in spin glass theory which leads to sharp phase transition in the Sherrington-Kirkpatrick theory if the coordination number. In ref. [8,9] we derived the non linear integral equation for distribution function f(Λ) of the form,

where the function D(x) includes f(Λ) and dipole-dipole interaction parameter. Sometimes it is impossible to derive general analytical expression for the distribution function and enough to analyze the properties of f(Λ) by its moments [18]. The expression for moments [8,9,18] include the parameters,

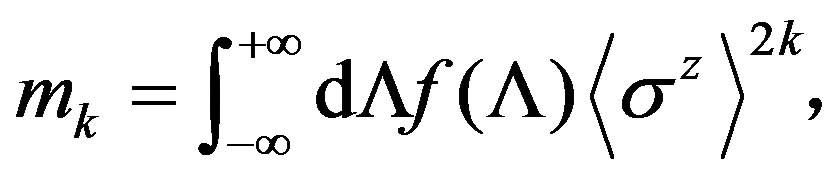
(k is integer).

These parameters depend on the temperature and they are the order parameters describing the phase transition into ordered spin glass phase from paramagnetic phase.

3. Dynamic Magnetic Susceptibility

Using the linear response theory [19] we derive longitudinal, dissipative component of the linear dynamic magnetic susceptibility averaged over configurations of the impurity magnetic dipoles of the following form,

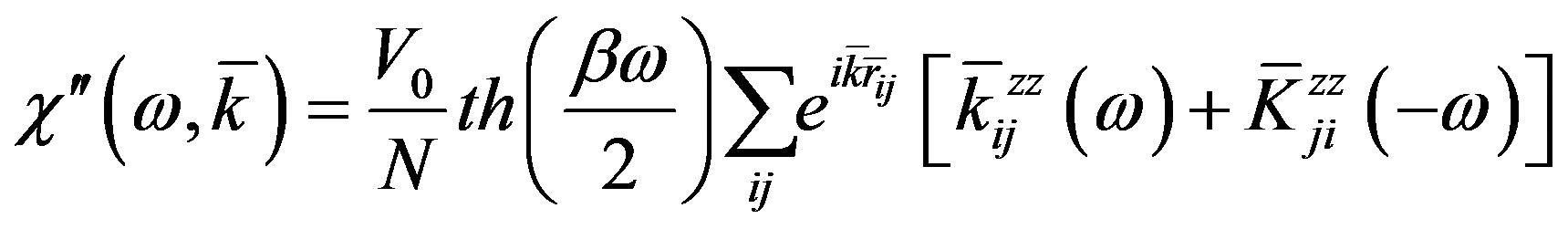(8)

where,

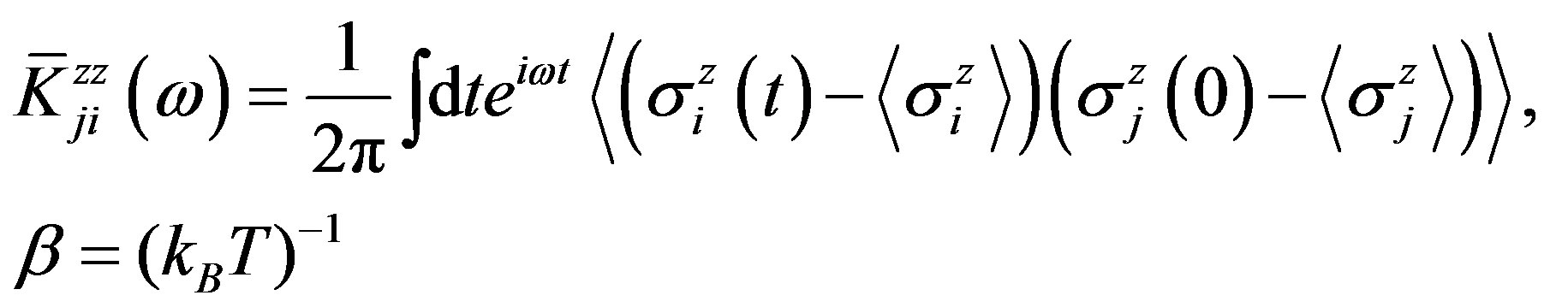
In Equation (8) the angular brackets means thermal average with the Hamiltonian, means the configurational averaging; k_B is the Boltzmann constant and T is the temperature of the system.

In order to calculate the correlation function (8) we use the temperature Green function of the form,

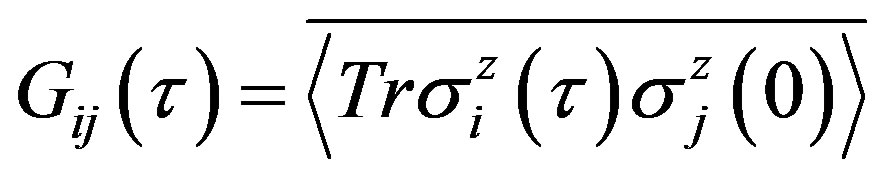(9)

where τ = it with.

Then the dissipative part of the susceptibility (8) may be represented as,

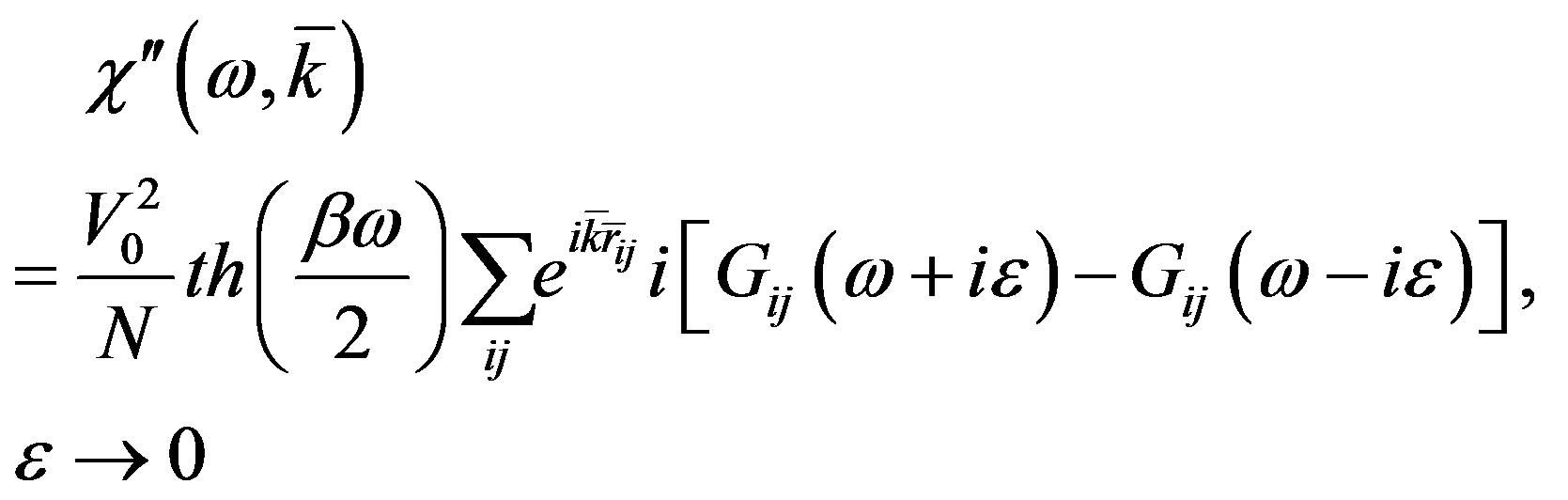(10)

This expression results from the spectral representation for the Fourier components of the Green function (9) which are analytically continued an all complex plane. The calculation of 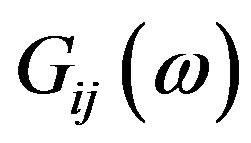is performed using diagrammatic technics developed in ref. [9-11]. The perturbation analysis is based on two small parameters: the inverse radius of the magnetic dipole-dipole interaction and the ratio.

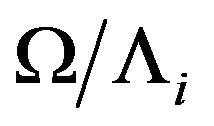As a result of our calculation we find the following expression for longitudinal, dissipative component of the dynamical magnetic susceptibility,

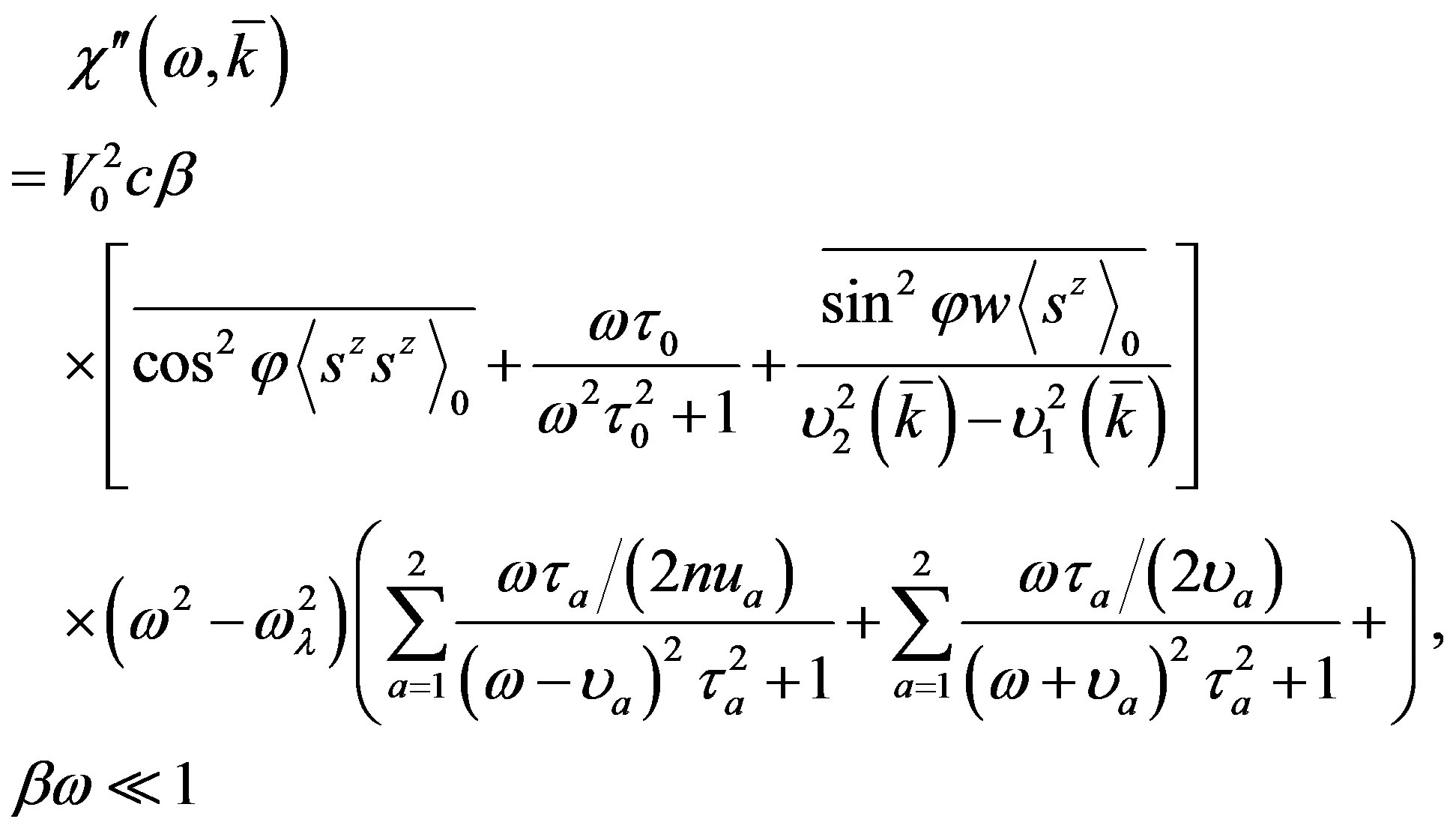(11)

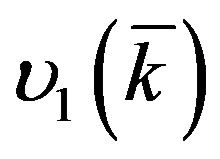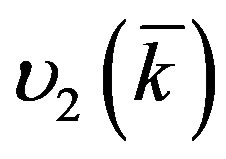where and are the frequencies of two branches (a = 1, 2) of the coupled collective dipolephonons excitations, c is the concentrations of the magnetic impurities.

In the long wave approximation the coupled dipolephonons excitations are given by the following expression describing two branches of these collective excitations (for details see ref. [11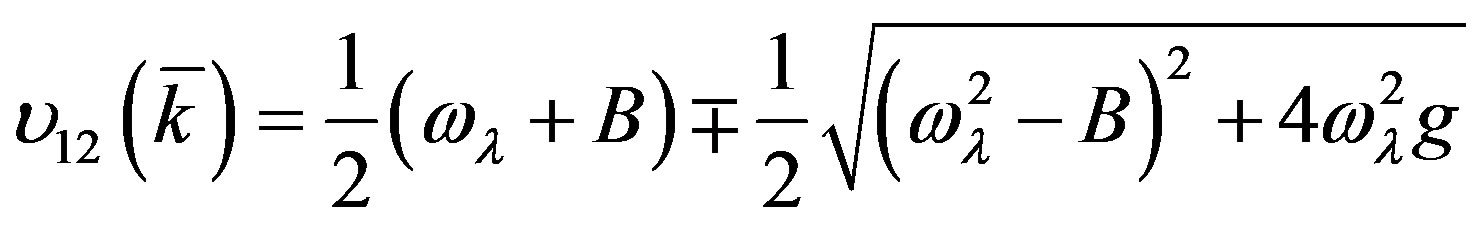,12]):

(12)

where,

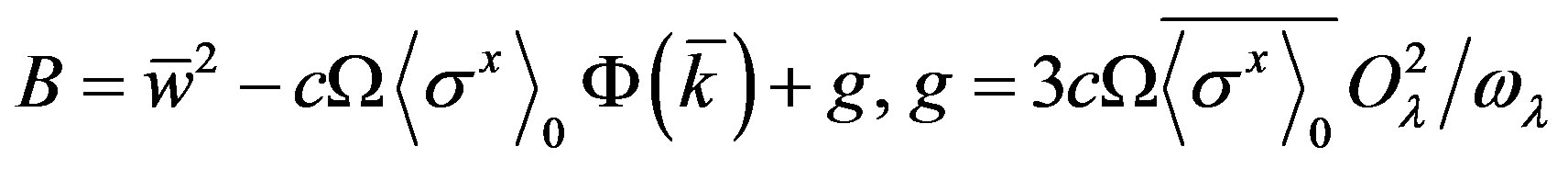(13)

is the Fourier transform of the general (direct and indirect) dipole-dipole interaction. We see from (12) that one of these models, namely υ₁ may be soft. The spectrum of Equation (12) is approximately linear over k as in usual spin glasses. This spectrum is anisotropic due to the anisotropy of the dipole-dipole interaction. The collective excitations are extended [11,12]. When the temperature goes to the spin glass phase transition temperature T_g then.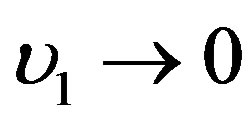

The times τ₀ and τ_a are determined in Equation (11) as following,

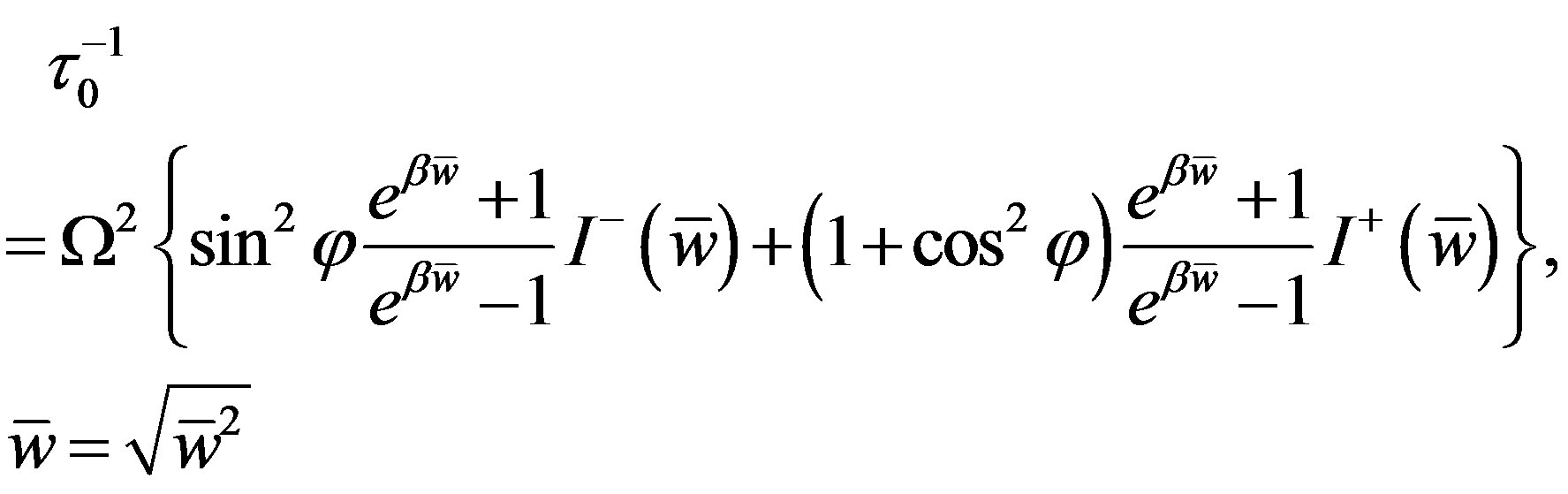(14)

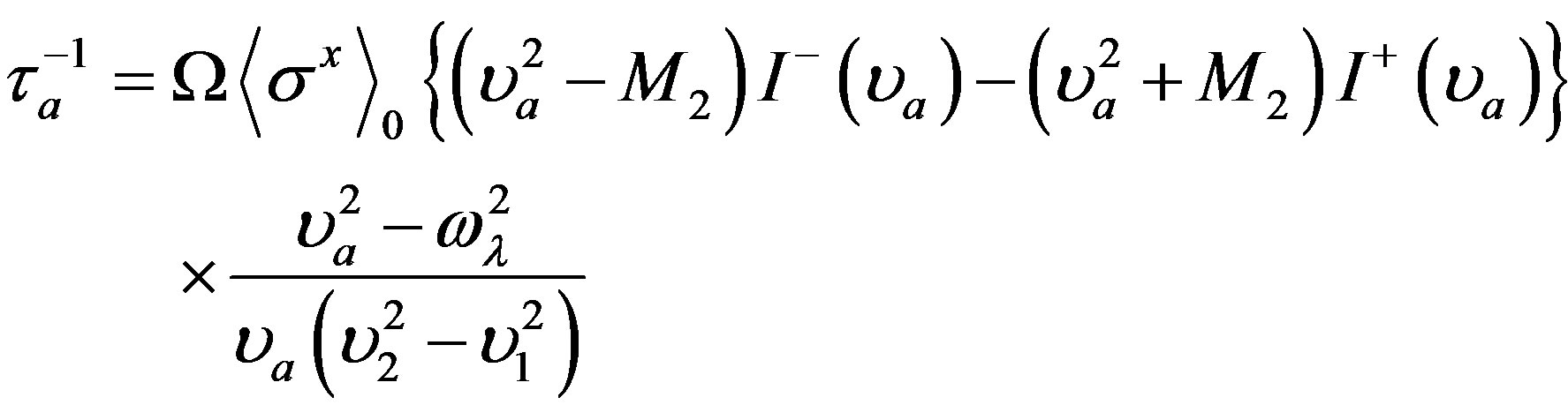(15)

where M₂ is the second moment of the distribution function of molecular fields, are the spectral functions of super-propagators, for which the simple asymptotic expressions are obtained in [9,11].

4. Discussion of the Results

From expression (11) we see that the magnetic dynamic susceptibility contains two contributions, 1) Relaxational which is proportional to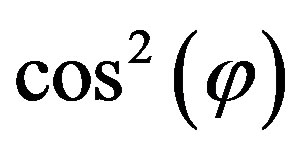; and 2) Resonance proportional to.

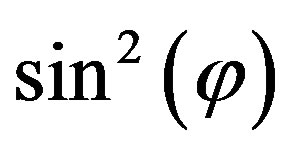If Ω < Λ, the relaxational absorption dominates (as in spin glass phase); on the contrary, the resonance absorption will be dominant is Ω >Λ.

The relaxation time τ₀ determines the width of the dissipative line at the spin glass phase,

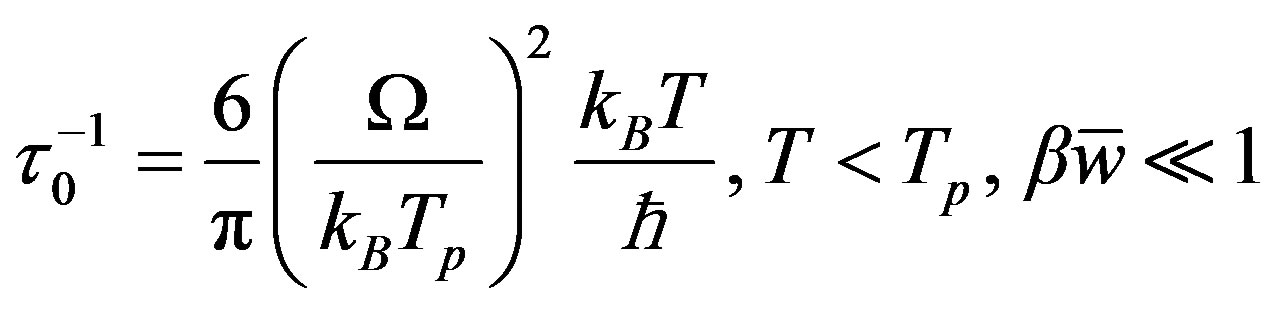
When the temperature grows, the relaxation rate increases exponentially,

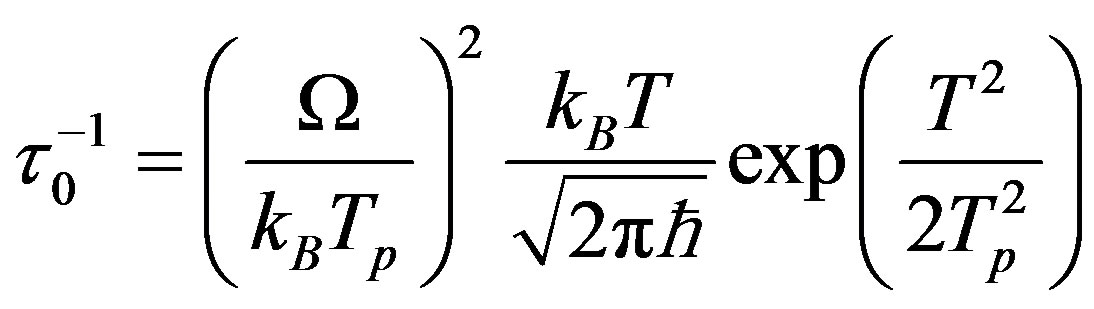(16)

The times τ_a (a = 1, 2) determine the life times of the coupled dipole-phonon collective excitations. The mode a = 1 is soft and due to the critical temperature dependence of the 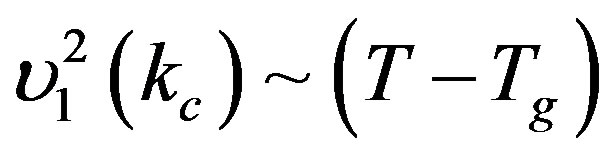we have the following asymptotic expression for (at) in low field regime,

(17)

where 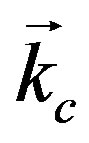is the wave vector of the condensation of the mode a = 1.

The resonant part of the magnetic susceptibility at 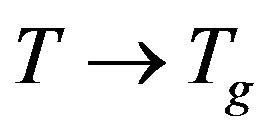results as,

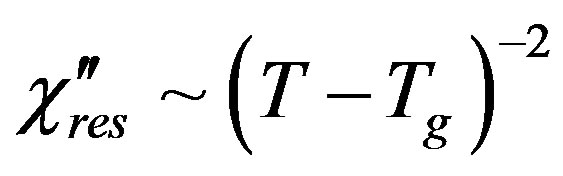
In the strong external field, the critical temperature dependence of the damping rate 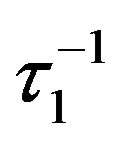is smoothed down 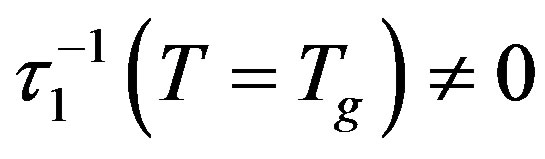giving the disappearance of the divergence of 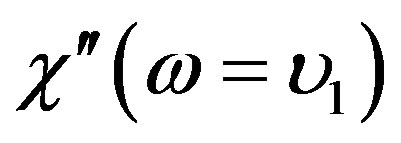as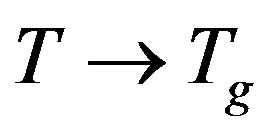. We note that the expression (15), for the resonance line width does not contain the contributions characteristic of the diluted system. These latter will be present to higher orders in our perturbation scheme.

The inhomogeneous width of the energy level in small field is determined only by width of the distribution function of molecular field which is proportional to the order parameter of the spin glass phase [8,18]. In paramagnetic phase m = 0, and, near Tg (spin glass phase) is.

Consider now the width of the absorption line due to the scattering of the collective excitations on the vacant sites of the lattice (in these sites the impurity dipoles are absent). This contribution 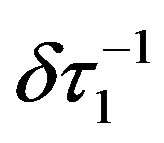is proportional to the concentration of the vacant sites 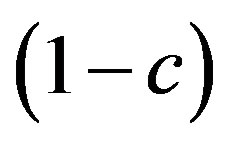and in a small external field at the transition from paramagnetic to spin glass phase. 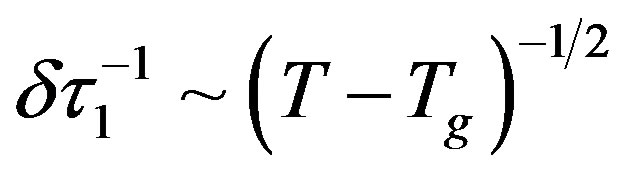Then the width of the absorption line will be proportional to at 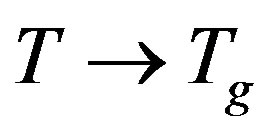giving a decreasing behaviour of the susceptibility proportional to 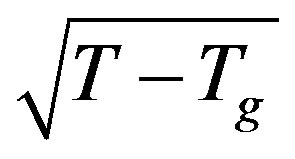at the frequency of the a.c. external field ω = υ₁. Due to the smoothing of the mode a = 1 at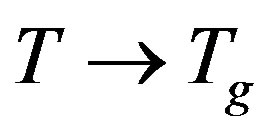, the resonance line width is constricted leading to an anomalous absorption increasing. When the dipole concentration grows this anomalous absorption also increases.

Measurements made at low temperature (helium temperature and below) of the linear dynamic magnetic susceptibility for systems with different values of the dipole concentration and at different temperatures give the possibility to observe these interesting anomalies. Many interesting properties observed for the dilute dipolar-coupled Ising magnetic LiHo_xY_1-xF₄ [3,7] are related , at least qualitatively, to our results, namely:

1) the growth of 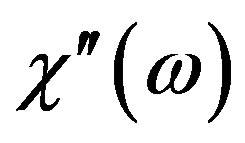approaching the transition temperature;

2) the concentration dependence of the linear susceptibility and;

3) the transverse field dependence of the susceptibility.

When we change the dipole impurity concentration, the effects of rejuvenation and memory may be observed by direct change in the spin-spin interaction (bond perturbation). In this paper we have also considered the effect of the magnetic dipole-phonon interaction on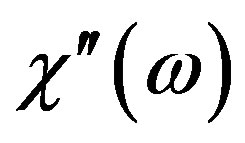. In the papers [9,11-13] we took into account the electric dipole-dipole interaction, direct and indirect (trough phonon field) considering other phenomena and for these disordered systems the role of the dipole-phonon interaction is more important.

Finally some years ago we have calculated the static and dynamic non linear magnetic susceptibility χ₃ for Ising spin glass model, revealing its divergence [20,21]. Measurement made on LiHo_xY_1-xF₄ system have confirmed such results [3,7].

REFERENCES