World Journal of Condensed Matter Physics
Vol.2 No.4(2012), Article ID:24404,6 pages DOI:10.4236/wjcmp.2012.24029
Magnetization of Nano-Size Subsystem in a Two-Dimensional Ising Square Lattice
![]()
1College of Science, Guangxi University for Nationalities, Nanning, China; 2Guangxi Key Laboratory of Hybrid Computational and IC Design Analysis, Nanning, China; 3College of Chemistry and Biological Engineering, Changsha University of Science and Technology, Changsha, China; 4College of Chemistry and Chemical Engineering, Central South University, Changsha, China.
Email: hlm66225@sohu.com
Received April 12th, 2012; revised May 19th, 2012; accepted June 2nd, 2012
Keywords: Magnetization; Ising Square Lattice; Nano-Size Subsystem
ABSTRACT
A two-dimensional Ising square lattice is modeled as a nano-size block array to study by Monte Carlo simulation the magnetic thermal stability of nano-structure magnetic media for data storage, thereon in the blocks J1 > 0 is assigned for the interaction of a pair of nearest-neighbor spins, while 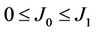 for that in regions between the blocks and
for that in regions between the blocks and 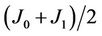 for the nearest-neighbor pairs with one in the block and the other one out of but near-most the block. We show that the magnetic thermal stability of the block accrues with the increase of J1 and with the decrease of J1 − J0 for a given J1, but contrarily, the anchoring ability for the initial magnetic orientation in nano-size block trails off as J1 − J0 diminish. This phenomena and size dependence of such anchoring ability are discussed in detail.
for the nearest-neighbor pairs with one in the block and the other one out of but near-most the block. We show that the magnetic thermal stability of the block accrues with the increase of J1 and with the decrease of J1 − J0 for a given J1, but contrarily, the anchoring ability for the initial magnetic orientation in nano-size block trails off as J1 − J0 diminish. This phenomena and size dependence of such anchoring ability are discussed in detail.
1. Introduction
Recently magnetic microstructure and nano-structure related to high-density magnetic recording, such as magnetic nanowires, chains, rings, planar arrays of magnetic nanoparticles and magnetic nano-structure thin film [1-3], is a topic of active research in material science. Practically, such microstructures are often imprinted on patterned substrate materials using lithography or beset in alloyed materials [4-6], which for practical applications are often imprinted using lithography on patterned substrate materials or doped with nanoparticles into alloyed ones [4-6]. That sophisticated techniques continue to be used to fabricate and characterize magnetic nano-structures assures the appearance of high density magnetic recording devices hereafter. Now, grains, as small as 7 - 8 nm, are used to store data at high signal-to-noise ratio (SNR) [7]. In the future, even smaller grains will be needed to store data at much higher areal densities. However, with the decreasing in size the particles will lose thermal stability, reaching the so called superparamagnetic limit, i.e., the magnetic orientation of particle at some size point no longer acts as magnetic bit due to thermal fluctuations [8,9]. Therefore the thermal stability in magnetic media for high density magnetic recording is still an open question.
In general, magnetic materials for data storage are composed of tiny but isolated magnetic nanocrystalline grains, but for magnetic nano-structure materials and nanoparticle materials, dipolar interactions between particles are unavoidable becoming relevant when increasing the packing density of the particles. This means that bit relevant is not a piddling issue in magnetic media for high density magnetic recording and the thermal stability of nanoparticle/unite of nano-structure materials must be considered in all of the system rather than as an isolator. Recently, a model of a two dimensional monodispersed array of single domain magnetic nanoparticles arranged in a square lattice was thus investigated to simulate thermal stability of magnetic media [10]. In that model each nanoparticle is a unite of the nano-structure material and is modeled as a giant magnetic moment, possessing saturated magnetism, that is, the magnetic moment interactions between particles and thermal fluctuation work only on the magnetic orientation, not changing the magnetic quantity of nanoparticle. Indeed, a nanoparticle is a cluster consisting of decades or hundreds of atoms/ions whose magnetic orientation ensemble is responsible for magnetization of nanoparticle. With the increase of temperature its magnetization will die away, reaching the superparamagnetic limit. Furthermore, the particles must further close up when continuing to heighten the density of magnetic recording, consequently here the interaction between particles is not taken as that of giant magnetic moments. Alike in bulk crystal, the interaction between two particles comes from the nearest-neighbor spin-spin interaction of atoms/ions respectively in their outer layers. If consider the influence of the atoms of substrate materials the correlation of two particles, based on the view of nearest-neighbor interaction, results from the interaction of their outer atoms with the atoms of substrate materials insulating them.
The Ising model has an enormous impact on modern physics in general and statistical physics, as well as in condensed matter physics for understanding the magnetism of materials [11,12]. In this paper, we provide a two-dimensional Ising square lattice which is modeled as a nano-size block array to study the magnetic thermal stability of nano-structure unite in magnetic media for data storage. As schematically delineated in Figure 1, in the blocks J1 > 0 is assigned for the interaction of a pair of nearest-neighbor spins, while 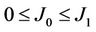 for that in regions between the blocks and
for that in regions between the blocks and  for the nearest-neighbor pairs with one in the block and the other one out of but near-most the block. Here J1 > 0 stipulates that the material in blocks/nanoparticles (acting as nanobits) is ferromagnetic, and
for the nearest-neighbor pairs with one in the block and the other one out of but near-most the block. Here J1 > 0 stipulates that the material in blocks/nanoparticles (acting as nanobits) is ferromagnetic, and 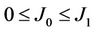 stands for the magnetic nature of media separating the particles from each other or for the interaction of nearest-neighbor spins in grain boundaries when they being close very much. For a binary Ag-Ni alloy, commonly the pairwise potential between different species of Ag and Ni atoms is assumed to be a mathematical or geometrical average function of the monoatomic potential [13,14]. Analogously we hence take the interaction of the nearest-neighbor pairs with one in the block and the other one out of but near-most the block as
stands for the magnetic nature of media separating the particles from each other or for the interaction of nearest-neighbor spins in grain boundaries when they being close very much. For a binary Ag-Ni alloy, commonly the pairwise potential between different species of Ag and Ni atoms is assumed to be a mathematical or geometrical average function of the monoatomic potential [13,14]. Analogously we hence take the interaction of the nearest-neighbor pairs with one in the block and the other one out of but near-most the block as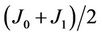 .
.
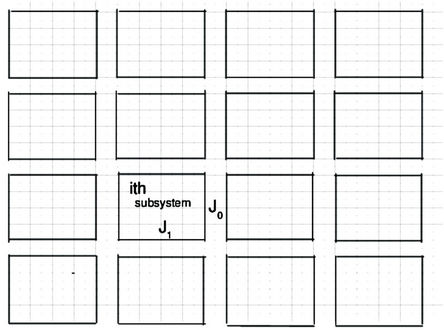
Figure 1. Schematic description of the Ising lattice model which is partitioned into blocks with each coated by patterned substrate material.
The Hamiltonian of our model is written as
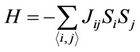 , (1)
, (1)
where Jij is the energy of spin-spin interaction which takes the values of J1,J0 and , respectively corresponding to the above three types of nearestneighbor spin pairs. The spins can only be in one of two states, either spin-up, Si = +1, or spin-down, Si = −1. The notation
, respectively corresponding to the above three types of nearestneighbor spin pairs. The spins can only be in one of two states, either spin-up, Si = +1, or spin-down, Si = −1. The notation 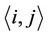 restricts the sum to run over all nearestneighbor pairs. It is noted that periodic boundary condition is implemented in this model. This Hamiltonian does not contain any information about its temporal evolution. Nevertheless, one can obtain good estimates for the average value of an observable quantity such as magnetization, susceptibility, free energy and specific heat by applying Metropolis Monte Carlo (MMC) simulation.
restricts the sum to run over all nearestneighbor pairs. It is noted that periodic boundary condition is implemented in this model. This Hamiltonian does not contain any information about its temporal evolution. Nevertheless, one can obtain good estimates for the average value of an observable quantity such as magnetization, susceptibility, free energy and specific heat by applying Metropolis Monte Carlo (MMC) simulation.
2. Methods
MMC has been used extensively in the researches of Ising models [15], which are described by a simple recipe: 1) Choose an initial state; 2) choose a site i; 3) calculate the energy change ∆E which results if the spin at site i is overturned; 4) generate a random number r such that ; 5) if
; 5) if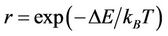 , flip the spin; 6) go to the next site and go to (III). For convenience in this paper, all energy scales are in units of the Boltzmann constant, which is set to kB = 1. Focusing on the magnetization of subsystem, we first investigate a Ising model which is of the size of 56 × 56 and partitioned into 4 × 4 blocks. These blocks are segregated from each other by patterned substrate material with the thickness of 4 sites and possess the size of 10 × 10. The cases of the model with other size will be discussed at the end of this paper. As an example, the block locating on the second row and second column, named as particle A in the following for convenience, is considered in the cases of J1 = 4.0 and
, flip the spin; 6) go to the next site and go to (III). For convenience in this paper, all energy scales are in units of the Boltzmann constant, which is set to kB = 1. Focusing on the magnetization of subsystem, we first investigate a Ising model which is of the size of 56 × 56 and partitioned into 4 × 4 blocks. These blocks are segregated from each other by patterned substrate material with the thickness of 4 sites and possess the size of 10 × 10. The cases of the model with other size will be discussed at the end of this paper. As an example, the block locating on the second row and second column, named as particle A in the following for convenience, is considered in the cases of J1 = 4.0 and . It is well-known that for ferromagnetic bulk material, i.e., Jij > 0, there is a phase transition from a disordered (paramagnetic) high-temperature phase to an ordered (ferromagnetic) low-temperature phase, and a continuous but abrupt pick-up of the average magnetization per spin can be anticipated at a temperature TC. In zero external field, the measured average magnetization would always be zero even for T < TC, since a finite system which is necessarily performed to emulate the bulk material remains ergodic even for T < TC. To surmount this puzzle, one of the simplest ways of emulating a system confined to a particular phase is to consider the average absolute magnetization per spin [11]. We found that when J1 ≥ 4.0 the time scaled by 105 MMC steps is long enough for system relaxing towards its equilibrium from an arbitrary initial state, during which the global spin inversion of the equilibrium state has not been observed. Therefore the average magnetization is still an observable quantity measured in the above time when J1 ≥ 4.0. Furthermore it is a necessarily quantity to character nanoparticle in the case of nanoparticle acting as nanobit. As mentioned above, we note that here the simulation results of the average magnetization, in terms of symmetry breaking, are suitable for bulk material consisting of the interacting nanoparticles. Under the same initial condition where Si takes the value randomly from +1 and −1, for the system at an arbitrary temperature T we perform MMC 105 steps and sample the microscopic states after 5 × 104 steps with the interval of 100 steps to obtain the average magnetization and susceptibility of particle A.
. It is well-known that for ferromagnetic bulk material, i.e., Jij > 0, there is a phase transition from a disordered (paramagnetic) high-temperature phase to an ordered (ferromagnetic) low-temperature phase, and a continuous but abrupt pick-up of the average magnetization per spin can be anticipated at a temperature TC. In zero external field, the measured average magnetization would always be zero even for T < TC, since a finite system which is necessarily performed to emulate the bulk material remains ergodic even for T < TC. To surmount this puzzle, one of the simplest ways of emulating a system confined to a particular phase is to consider the average absolute magnetization per spin [11]. We found that when J1 ≥ 4.0 the time scaled by 105 MMC steps is long enough for system relaxing towards its equilibrium from an arbitrary initial state, during which the global spin inversion of the equilibrium state has not been observed. Therefore the average magnetization is still an observable quantity measured in the above time when J1 ≥ 4.0. Furthermore it is a necessarily quantity to character nanoparticle in the case of nanoparticle acting as nanobit. As mentioned above, we note that here the simulation results of the average magnetization, in terms of symmetry breaking, are suitable for bulk material consisting of the interacting nanoparticles. Under the same initial condition where Si takes the value randomly from +1 and −1, for the system at an arbitrary temperature T we perform MMC 105 steps and sample the microscopic states after 5 × 104 steps with the interval of 100 steps to obtain the average magnetization and susceptibility of particle A.
3. Result and Discussion
We denote the absolute value of average magnetization per spin as 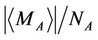 and susceptibility per spin of particle A as χA. In the cases of J0 = 0.0, 1.5, 3.0, 4.0, the functions of the absolute value of average magnetization per spin and susceptibility per spin of particle A with respective to temperature T are plotted together in Figure 2. It is found from Figure 2 that there exists a disordered (paramagnetic) high-temperature phase and an ordered (ferromagnetic) low-temperature phase. This can be interpreted by the free energy of particle A,
and susceptibility per spin of particle A as χA. In the cases of J0 = 0.0, 1.5, 3.0, 4.0, the functions of the absolute value of average magnetization per spin and susceptibility per spin of particle A with respective to temperature T are plotted together in Figure 2. It is found from Figure 2 that there exists a disordered (paramagnetic) high-temperature phase and an ordered (ferromagnetic) low-temperature phase. This can be interpreted by the free energy of particle A, 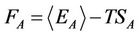 , where SA is its entropy. At relatively high temperatures, the case of
, where SA is its entropy. At relatively high temperatures, the case of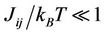 , the term TSA dominates so that the free energy FA is minimized by maximizing the entropy, corresponding to paramagnetic phase where the spins orientate randomly; while at relatively low temperatures, the case of
, the term TSA dominates so that the free energy FA is minimized by maximizing the entropy, corresponding to paramagnetic phase where the spins orientate randomly; while at relatively low temperatures, the case of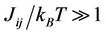 , the interaction energy
, the interaction energy 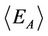 dominates so that the free energy is minimized by minimizing the energy, corresponding to ferromagnetic phase where the spins orienttate to the same direction; and when the thermal energy TSA and the interaction energy
dominates so that the free energy is minimized by minimizing the energy, corresponding to ferromagnetic phase where the spins orienttate to the same direction; and when the thermal energy TSA and the interaction energy 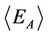 are comparable, i.e., when T ≈ TC, phase transition between ferromagnetic phase and paramagnetic phase occurs. Theoretically, as T approaches the critical temperature TC, the susceptibility per spin χ diverges. Therefore the temperature corresponding to the peak value of the function of χ versus T can be roughly taken as the value of TC. It is well known that the susceptibility per spin χ can be obtained from the variance of the magnetization of system, formulated as follow [11],
are comparable, i.e., when T ≈ TC, phase transition between ferromagnetic phase and paramagnetic phase occurs. Theoretically, as T approaches the critical temperature TC, the susceptibility per spin χ diverges. Therefore the temperature corresponding to the peak value of the function of χ versus T can be roughly taken as the value of TC. It is well known that the susceptibility per spin χ can be obtained from the variance of the magnetization of system, formulated as follow [11],
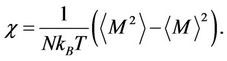 (2)
(2)
So as shown in Figure 2(b), that TC increases with the decreasing of J1 – J0 illuminates that the temperature variance range for the particle (nanobit) in ferromagnetic phase becomes larger and larger as J1 – J0 decreases,

Figure 2. The functions of the absolute value of average magnetization per spin 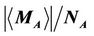 and susceptibility per spin χA of particle A vs. temperature T, in the cases of J1 = 4.0 and J0 = 0.0, 1.5, 3.0, 4.0, respectively, where NA is the number of sites in particle A, and the increment of T is 0.5.
and susceptibility per spin χA of particle A vs. temperature T, in the cases of J1 = 4.0 and J0 = 0.0, 1.5, 3.0, 4.0, respectively, where NA is the number of sites in particle A, and the increment of T is 0.5.
meaning that the magnetic thermal stability of the particle accrues when J1 – J0 trails off.
What is related closely to the susceptibility is spin-spin correlation function defined as
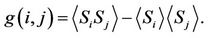 (3)
(3)
Based on Equation (3) the susceptibility χ can be written as
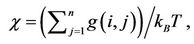
which is the analogue in percolation describing how site-site correlation function is related to the average cluster size or to the average correlation length [11]. It is known that for an infinite system, in the low temperature phase the correlation length increases with increasing of the temperature and diverges as the temperature approaches the critical temperature TC; while for a finite system the correlation length reaches its peak value at the critical temperature TC. To explore block-block correlation, we define the correlation of total spins of particle A with those of its four nearest-neighbor particles as
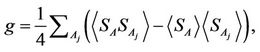
where Aj = 1, 2, 3, 4 stand for the left, the right, the down, the up particles, respectively. Figure 3 shows that the correlation of total spins of particle A with those of its four nearest-neighbor particles is a function of J0. Comparing Figure 3 with Figure 2(b), one can see that at temperature T = 9.0, g(J0 = 3.0) > g(J0 = 1.5) > g(J0 = 0.0) accords with χA(J0 = 3.0) > χA(J0 = 1.5) > χA(J0 = 0.0), as well as g(J0 = 4.0) versus χA(J0 = 4.0). It accounts for that the magnetic thermal stability of the particle A having

Figure 3. The plot for the mean value of the correlation function g in the fluctuation of total spins of particle A and those of its four nearest-neighbor particles (blocks) vs. J0 at temperature T = 9.0, where J1 = 4.0.
relationship with J0 indicates the relevance of the particle A with the other particles, bridged by substrate material.
Further to understand magnetic thermal stability of the block, the fluctuation in magnetization of particle A,

with respect to temperature T are plotted on Figure 4. Here, D1 describes the relative deviation of magnetization MA to its average value. Figure 4 shows that with increasing of temperature T the fluctuation of magnetization MA becomes severe and particle A will lose its magnetization when it is in paramagnetic phase; further more, D1 augments in the range of 0.05 ≤ D1 ≤ 0.20 as 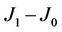 reduces for a given J1 or increases with the increasing of J1. Thus one may conclude that in fluctuation criterion of D1 ≤ D1C, e.g., D1 ≤ 0.1, particles acting as nanobits can be used to storage data at higher temperature when
reduces for a given J1 or increases with the increasing of J1. Thus one may conclude that in fluctuation criterion of D1 ≤ D1C, e.g., D1 ≤ 0.1, particles acting as nanobits can be used to storage data at higher temperature when 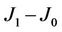 is smaller than that when
is smaller than that when  is large in the case of J1 being fixed.
is large in the case of J1 being fixed.
However, in the magnetic media for data storage, what must be kept and be ensured not fluctuating intensity with the change of temperature T are particles’ initial magnetic states. After the finish of the writing information on magnetic media, i.e., with the applied field being switched off, the information bit has been recorded by the reversed spins Si in particle and is represented by its total magnetization MA with an orientation (say up or down). The fluctuation of magnetization D1 does not contain any information about the initial magnetic state of particle. Therefore instead of D1, we compute the fluctuation of magnetization D2, which defined as
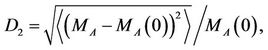
where MA(0) is the initial total magnetization of particle

Figure 4. The functions of the fluctuation in magnetization of particle A, D1, with respect to temperature T in the cases of (J1, J0): (4.0, 0.0) , (4.0, 1.0) , (4.0, 1.5) , (4.0, 3.0), (4.0, 4.0) and (6.0, 1.0).
A. D2 describes the relative deviation of magnetization MA to its initial total magnetization. Note that here we initialize the system with Si(0) = 1 if site in particle A, otherwise Si(0) = –1. D2 = 0 means that MA = MA(0), while D2 = 2.0 means that MA = −MA(0). Thus Figure 5 shows that in the cases of  being large, say (J1, J0): (4.0, 0), (4, 1), (4, 1.5) and (6, 1), the initial magnetic state of particle A can be kept down when it is in feromagnetic phase, but the initial magnetic state will be lost with the spin in particle A Si = –1 ≠ Si(0) = 1 in the case of
being large, say (J1, J0): (4.0, 0), (4, 1), (4, 1.5) and (6, 1), the initial magnetic state of particle A can be kept down when it is in feromagnetic phase, but the initial magnetic state will be lost with the spin in particle A Si = –1 ≠ Si(0) = 1 in the case of 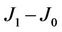 being small, e.g., (J1, J0): (4, 3) and (4, 4). For clarity, sixteen microstates of the system being in equilibrium states evolving from the initial state mentioned above are shown in Figure 6, corresponding respectively to different J1 and J0 at temperature T = 2, 4, 6, 12. It is consistent with Figure 5. Up to now we thus conclude that the magnetic thermal stability of the block accrues with the increase of J1 and with the decrease of
being small, e.g., (J1, J0): (4, 3) and (4, 4). For clarity, sixteen microstates of the system being in equilibrium states evolving from the initial state mentioned above are shown in Figure 6, corresponding respectively to different J1 and J0 at temperature T = 2, 4, 6, 12. It is consistent with Figure 5. Up to now we thus conclude that the magnetic thermal stability of the block accrues with the increase of J1 and with the decrease of 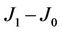 for a given J1, but contrarily, the ability for the initial magnetic orientation kept in nano-size block, named as anchoring ability of initial magnetization, trails off as
for a given J1, but contrarily, the ability for the initial magnetic orientation kept in nano-size block, named as anchoring ability of initial magnetization, trails off as 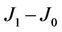 diminishes.
diminishes.
The above discussions are based on the two dimensional Ising square lattice with size 56 × 56, in which the blocks with size 10 × 10 are segregated from each other by patterned substrate material with the thickness of 4 sites. With the decreasing of particle size the thermal fluctuations induce random flipping of the magnetic moment with time so that nanoparticles lose their stable magnetic order and become superparamagnetic. V. Skumryev and coworkers [16] had studied the systems where ferromagnetic cobalt nanoparticles of about 4 nm in diameter that are embedded in either a paramagnetic or an antiferromagnetic matrix. They found that the cobalt cores lose their magnetic moment at temperature being
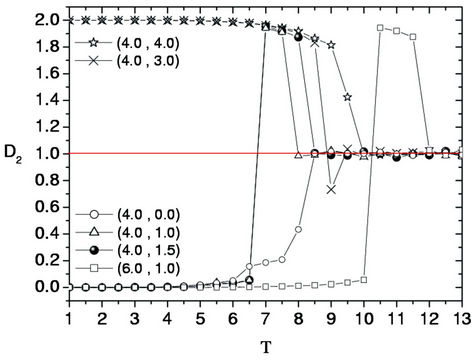
Figure 5. The functions of the fluctuation in magnetization of particle A, D2, with respect to temperature T in the cases of (J1, J0): (4.0, 0.0), (4.0, 1.0), (4.0, 1.5), (4.0, 3.0), (4.0, 4.0) and (6.0, 1.0), respectively.

Figure 6. Sixteen microstates characterizing the system in equilibrium states for temperature T = 2, 4, 6, 12 from left to right and for (J1, J0): (4.0, 3.0), (6.0, 1.0), (4.0, 1.0), (4.0, 0.1) from bottom to top, respectively. Sites containing upspins are white while sites containing down-spins are gray.
10 K in the first system but remain ferromagnetic up to about 290 K in the second. Similarly here for paramagnetic substrate material, we investigate theoretically the size dependence of temperature T0 based on the criterion D1 ≥ 0.1, i.e., D1 ≥ 0.1 if temperature T ≥ T0. For this purpose, the two-dimensional Ising square lattices are set to be 200 × 200, which are partitioned by the blocks with size of 6 × 6, 16 × 16, 21 × 21, 36 × 36 and 46 × 46, respectively, segregated from each other by patterned substrate material with the thickness of 4 sites. From Figure 7 one can deduces 1) that for a given value of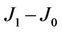 , T0 increases with increasing the particle’s size NA and will reach its saturated value; 2) that for a given NA, T0 becomes large as
, T0 increases with increasing the particle’s size NA and will reach its saturated value; 2) that for a given NA, T0 becomes large as 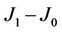 decreases if NA is smaller and such change is not distinct anymore if NA is larger. This
decreases if NA is smaller and such change is not distinct anymore if NA is larger. This

Figure 7. The size dependence of T0 larger than which when temperature T is, D1 ≥ 0.1 corresponding respectively to different values of J1 − J0. The size of lattices are 200 × 200, thereon the size of blocks are NA × NA with NA = 6, 16, 21, 36 and 46, respectively, segregated from each other by patterned substrate material with the thickness of 4 sites. Also, periodic boundary condition is implemented. The temperature increment for searching T0 is 0.2.
may be explained as following. Reckon the sites in patterned substrate material coating the particle as its shell, with the increasing of the size of particle, the surface sites (shell’s sites) to core sites (particle’s sites) ratio decreases and the effects induced by surface become weak, that is, the properties of particle are dominated by itself, thereby it behaves like bulk material disregard of the patterned substrate material and can be considered as a isolated bulk system.
4. Conclusions
Based on the pair interaction of nearest neighbor spins in a two-dimensional Ising square lattice, we have investigated the thermal stability of magnetization of ferromagnetic nano-size subsystems separated by paramagnetic substrate material. The interaction for spins in subsystem is denoted as J1 while that for spins in substrate material is J0. It has been found that the magnetic thermal stability of the nano-subsystem accrues with the increase of J1 and with the decrease of 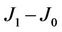 for a given J1, but contrarily, the anchoring ability for the initial magnetic orientation in nano-size subsystem trails off as
for a given J1, but contrarily, the anchoring ability for the initial magnetic orientation in nano-size subsystem trails off as 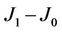 diminishes. In addition, with increasing the subsystem’s size its magnetization behaves like that of bulk material, disregard of the patterned substrate material and being able to considered as a isolated bulk system. These results can be used to understand high-density magnetic nanoparticle material for data storage and superparamagnetic limit. Also, it may proposed some ways to enhance the storage density of recording magnetic media by reducing the size of particle: 1) Increasing the spin interaction in ferromagnetic nanoparticle, i.e., increasing
diminishes. In addition, with increasing the subsystem’s size its magnetization behaves like that of bulk material, disregard of the patterned substrate material and being able to considered as a isolated bulk system. These results can be used to understand high-density magnetic nanoparticle material for data storage and superparamagnetic limit. Also, it may proposed some ways to enhance the storage density of recording magnetic media by reducing the size of particle: 1) Increasing the spin interaction in ferromagnetic nanoparticle, i.e., increasing ; 2) For a fixed spin interaction in ferromagnetic nanoparticle, selecting suitable J0 to make nanoparticle meeting both thermal fluctuation criterions D1 and D2 is more available than that coating nanoparticle by nonmagnetic substrate material (i.e., the case of J0 = 0), for in the former case the nanoparticle can keep its initial magnetization state at a higher temperature.
; 2) For a fixed spin interaction in ferromagnetic nanoparticle, selecting suitable J0 to make nanoparticle meeting both thermal fluctuation criterions D1 and D2 is more available than that coating nanoparticle by nonmagnetic substrate material (i.e., the case of J0 = 0), for in the former case the nanoparticle can keep its initial magnetization state at a higher temperature.
The authors acknowledge the finance supports from the Department of Education of Guangxi (200911MS78), the Ministry of Education Science and Technology Key Project under Grant 210164 and Grants (HCIC201103) of Guangxi Key Laboratory of Hybrid Computational and IC Design Analysis Open fund, National Natural Science Foundation of China (Grant No. 21171174), and Hunan Provincial Science and Technology Projects (Grant No. 2011 GK3115).
REFERENCES
- E. Rafal, T. Kasama, A. Wei, S. L. Tripp, M. J. Hytch, E. Snoeck, R. J. Harrison and A. Putnis, “Off-Axis Electron Holography of Magnetic Nanowirse and Chains, Rings, and Planar Arrays of Magnetic Nanoparticles,” Microscopy Research and Technique, Vol. 64, No. 5-6, 2004, pp. 390-402.
- D. F. Wang, A. Takahashi, Y. Matsumoto, K. M. Itoh, Y. Yamamoto, T. Ono and M. Esash, “Magnetic Mesa Structures Fabricated Reactive Ion Etching with CO/NH3/Xe Plasma Chemistry for an All-Silicon Quantum Computer,” Nanotechnology, Vol. 16, No. 6, 2005, pp. 990- 994. doi:10.1088/0957-4484/16/6/062
- R. F. Service, “Is the Terabit Within Reach?” Science, Vol. 314, No. 5807, 2006, pp. 1868-1870. doi:10.1126/science.314.5807.1868
- R. Sbiaa and S. N. Piramanayagam, “Patterned Media towards Nano-Bit Magnetic Recording: Fabrication and Challenges,” Recent Patents on Nanotechnology, Vol. 1, No. 1, 2007, pp. 29-40. doi:10.2174/187221007779814754
- F. Golmar, M. Villafuerte, A. M. Navarro, C. E. R. Torres, J. Barzola-Quiquia, P. Esquinazi and S. P. Heluani, ZnO:Co Diluted Magnetic Semiconductor or Hybrid Nanostructure for Spintronics,” Journal of Materials Science , Vol. 45, No. 22, 2010, pp. 6174-6178.
- Q. Jie, J. Zhou, X. Shi, I. K. Dimitrov and Q. Li, “Strong Impact of Grain Boundaries on the Thermoelectric Properties of Non-Equilibrium Synthesized p-Type Ce1.05Fe4Sb12.04 Filled Skutterudites with Nanostructure,” arXiv: 1006.5715v1, 2010.
- G. Choe, B. R. Acharya, K. E. Johnson and K. J. Lee, “Transition and DC Noise Characteristics of Longitudinal Oriented Media,” IEEE Transactions on Magnetics, Vol. 39, No. 5, 2003, pp. 2264-2266. doi:10.1109/TMAG.2003.816266
- J. L. García-Palacios and F. J. Lázaro, “Langevin Dynamics Dynamics Study of the Dynamical Properties of Small Magnetic Particles,” Physical Review B, Vol. 58, No. 22, 1998, pp. 14937-14958. doi:10.1103/PhysRevB.58.14937
- W. T. Coffey, D. S. F. Crothers, J. L. Dormann, Yu. P. Kalmykov, E. C. Kennedy and W. Wernsdorfer, “Thermally Activated Relaxation Time of a Single Domain Ferromagnetic Particle Subjected to a Uniform Field at an Oblique Angle to the Easy Axis: Comparison with Experimental Observations,” Physical Review Letters, Vol. 80, No. 25, 1998, pp. 5655-5658. doi:10.1103/PhysRevLett.80.5655
- D. A. Stariolo and O. V. Billoni, “Dipolar Interactions and Thermal Stability of Two-Dimensional Nanoparticle Arrays,” Journal of Physics D: Applied Physics, Vol. 41, 2008, 7 p.
- K. Christensen and N. R. Moloney, “Complexity and Criticality,” Imperial College Press, London, 2005. doi:10.1142/p365
- K. binde and W. Kob, “Glassy Materials and Disordered Solids: An Introduction to Their Statistical Mechanics,” World Scientific Publishing Co., Singapore City, 2005.
- M. S. Daw and M. I. Baskes, “Semiempirical, Quantum Mechanical Calculation of Hydrogen Embrittlement in Metals,” Physical Review Letters, Vol. 50, No. 17, 1983, pp. 1285-1288. doi:10.1103/PhysRevLett.50.1285
- S. M. Foiles, “Calculation of the Surface Segregation of Ni-Cu Alloys with the Use of the Embedded-Atom Method,” Physical Review B, Vol. 32, No. 12, 1985, pp. 7685- 7693. doi:10.1103/PhysRevB.32.7685
- D. K. Landau and K. Binder, “A Guide to Monte Carlo Simulations in Statistical Physics,” World Scientific Publishing Co., Singapore, 2000.
- V. Skumryev, S. Stoyanov, Y. Zhang, G. Hadjipanayis, D. Givord and J. Nogués, “Beating the Superparamagnetic Limit with Exchange Bias,” Nature, Vol. 423, 2003, pp. 850-853. doi:10.1038/nature01687

