World Journal of Condensed Matter Physics
Vol.1 No.3(2011), Article ID:6928,7 pages DOI:10.4236/wjcmp.2011.13011
Ab Initio Calculations of Optical Properties of TlBr and TlCl Radiation Detectors
![]()
Department of Physics, United Arab Emirates University, Al-Ain, United Arab Emirates.
Email: amranen@yahoo.com, amrane@gmail.com
Received March 8th, 2011; revised May 2nd, 2011; accepted May 15th, 2011.
Keywords: Plane Wave Method, Dielectric Function, Reflectivity, Refractive Index, Coefficient of Absorption
ABSTRACT
We report on ab initio calculations of the optical properties of TlBr and TlCl binary semiconductor compounds using the self-consistent scalar relativistic full potential linear augmented plane wave band method (FP-LAPW) within the local density approximation (LDA) including the generalized gradient approximation (GGA). The accurate calculations of linear optical function (refractive index, reflectance, coefficient of absorption, and both imaginary and real dielectric function) is performed in the photon energy range up to 20 eV. The predicted optical constants agree well with the available experimental data.
1. Introduction
Thallium halides (TlCl and TlBr) are technologically very important materials having many applications as radiation detectors and as new optical fibre crystals. Thallium chloride and thallium bromide both, crystallize in the cubic CsCl structure. This structure, with a coordination number of eight, represents the most stable dense configuration for ionic crystals [1-3].
Most of the heavy-metal halides crystallize into anisotropic or layered structures. On the other hand the crystal structure of TIC1 and T1Br is simple; the space lattice is simple cubic (CsCI type). The simple lattice structure would reduce the complexity of electronic structure usually encountered in anisotropic materials and allow us a simple analysis of the optical spectra. Optical properties of TIC1 and T1Br have been studied by many workers in the absorption edge [4] and in the VUV region [5,6]. A remarkable property of thallium halide crystals is their high dielectric permittivity. The static values are 30 and 32 for the cubic TlBr and TlCl [7-9].
Thallium halogenides TlX (X—Cl, Br, I) are also widely used in optical engineering due to their high transparence in a wide range of wavelengths and high radiation resistance. They are promising for fabricating fiber-optical waveguides [10]. However, the electronic structures of these materials are poorly understood. For TlCl, the transmission spectra of films in the range 3 - 6 eV [11], the characteristic electron loss spectra [12], and theoretical dispersions of four valence and four conduction bands are known [13,14]. In addition, the energies of interband transitions are determined for TlCl in a narrow energy range (3 - 6 eV) only for X and R points and a middle point of the ΓM direction [14].
In this study, we have investigated the optical properties by means of first-principles density-functional total-energy calculation using the all-electron full potential linear augmented plane-wave method (FPLAPW).
2. Calculations
Scalar relativistic calculations have been performed using the wien2k code [15,16]. For the exchange correlation potential, we have used the local density approximation (LDA) with a parameterization of Ceperly-Adler data [17]. The new Full Potential Augmented Plane Wave method of the density functional theory is applied [18,19]. Several improvements to solve the energy dependence of the basis set were tried but the first really successful one was the linearization scheme introduced by Andersen [20] leading to the linearized augmented plane wave (LAPW) method. In LAPW, the energy dependence of each radial wave function inside the atomic sphere is linearized by taking a linear combination of a solution u at a fixed linearization energy and its energy derivative 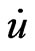 computed at the same energy.
computed at the same energy.
 (1)
(1)
where  = r – rα is the position inside sphere α with polar coordinates
= r – rα is the position inside sphere α with polar coordinates 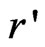 and r, k is a wave vector in the irreducible Brillouin zone, K is a reciprocal lattice vector and
and r, k is a wave vector in the irreducible Brillouin zone, K is a reciprocal lattice vector and 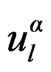 is the numerical solution to the radial Schrodinger equation at the energy ε. The coefficients
is the numerical solution to the radial Schrodinger equation at the energy ε. The coefficients  are chosen such that the atomic functions for all L components match (in value) the PW with K at the Muffin tin sphere boundary. The KS orbitals are expressed as a linear combinations of APWs
are chosen such that the atomic functions for all L components match (in value) the PW with K at the Muffin tin sphere boundary. The KS orbitals are expressed as a linear combinations of APWs . In 1991 Singh [21] introduced the concept of local orbitals (LOs) which allow an efficient treatment of the semi-core states. An LO is constructed by the LAPW radial functions u and
. In 1991 Singh [21] introduced the concept of local orbitals (LOs) which allow an efficient treatment of the semi-core states. An LO is constructed by the LAPW radial functions u and  at one energy ε1 in the valence band region and a third radial function at ε2 (see Equation (2)).
at one energy ε1 in the valence band region and a third radial function at ε2 (see Equation (2)).
Recently, an alternative approach was proposed by Sjöstedt et al [22], namely the APLW+ lo (local orbital) method. Here the augmentation is similar to the original APW scheme but each radial wavefunction is computed at fixed linearization energy to avoid the non-linear eigenvalue problem. The missing variational freedom of the radial wavefunctions can be recovered by adding another type of local orbitals (termed in lower case to distinguish them from LO) containing u and 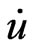 term:
term:
 (3)
(3)
It was demonstrated that this new scheme converges faster than LAPW. The APW + lo scheme has been implemented in the wien2k code version [23].
However, in the calculations reported here, we chose the muffin tin radii for Tl, Br and Cl to be 2.5 a.u. The expansion of the spherical region is developed up to lmax = 10 for both compounds, while in the interstitial region we have used 372 plane waves for TlBr and 331 for TlCl. Furthermore, we have used the energy cut-off of RMT·Kmax = 8 and the maximal reciprocal vector equal to 10 for both compounds.
The integrals over the Brillouin zone are performed using the Monkorst-pack special k-points approach [24]. Since calculations of the optical properties require a denser k-matrix, we have used 1000 k-points in the irreducible Brillouin zone for integration in reciprocal space.
Optical properties of a solid are usually described in terms of the complex dielectric function 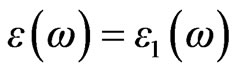 +
+ 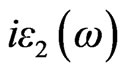 The dielectric function is determined mainly by the transition between the valence and conduction bands according to perturbation theory; the imaginary part of the dielectric function in the long wavelength limit has been obtained directly from the electronic structure calculation, using the joint density of states (DOS) and the optical matrix elements. It is expressed as Equation (4), where m is the mass and e the electrical charge of the electron,
The dielectric function is determined mainly by the transition between the valence and conduction bands according to perturbation theory; the imaginary part of the dielectric function in the long wavelength limit has been obtained directly from the electronic structure calculation, using the joint density of states (DOS) and the optical matrix elements. It is expressed as Equation (4), where m is the mass and e the electrical charge of the electron,  means the summation between all the conduction bands (l) and valence bands (n); and Pnl expresses the momentum matrix element between l and n. It is given by
means the summation between all the conduction bands (l) and valence bands (n); and Pnl expresses the momentum matrix element between l and n. It is given by
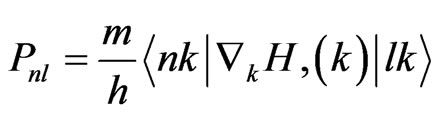
where H(k) is the Hamiltonian, and  are the k-space wavefunctions. Using the FP-LAPW parameters, we can directly calculate Pnl.
are the k-space wavefunctions. Using the FP-LAPW parameters, we can directly calculate Pnl.
The real part of the dielectric function can be derived from the imaginary part by the Kramers-Kronig relationship. The knowledge of both the real and the imaginary parts of the dielectric allows the calculation of important optical functions. In this paper, we also present and analyze the refractive index  given by
given by
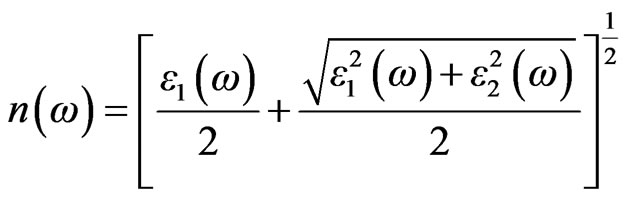 (5)
(5)
At low frequency (ω = 0), we get the following relation:

To correct the LDA error in the band gaps a constant potential was applied to the conduction band states (using the scissors operator which rigidly shifts the conduction band states) in order to match the calculated band gaps with the experimental data.
3. Results
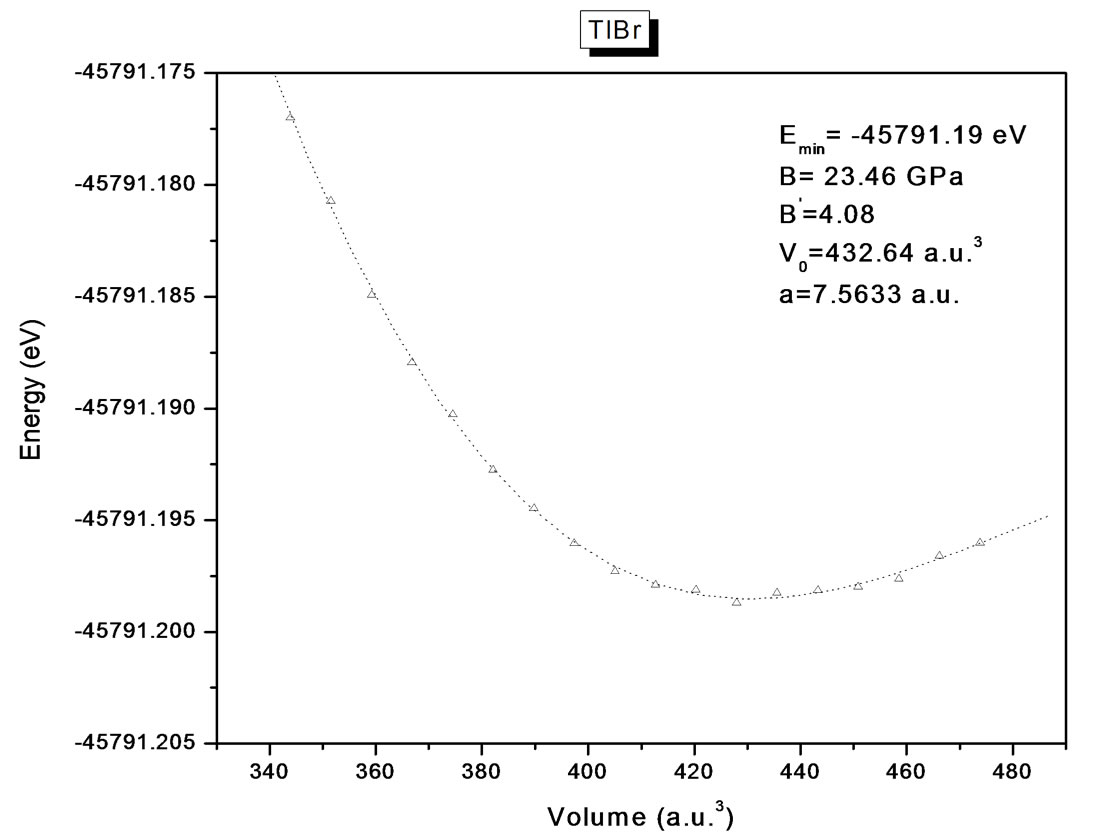
3.1. Total Energy Minimization
The structural optimization of the cubic phase was performed by calculating the total energy as function of the volume. The minimization of the total energy versus volume requires that each of the self-consistent calculations is converged, so the iteration process was repeated until the calculated total energy of the crystal converged to less than 1 mRyd. A total of seven iterations was necessary to achieve self-consistency for TlBr and nine iteration in the case of TlCl. The equilibrium lattice constants and bulk modulus are calculated by fitting the total
 (2)
(2)
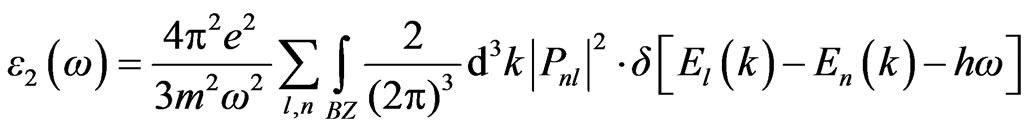 (4)
(4)
energy versus volume according to Murnaghan’s equation of state [25]. The variation of total energy as a function of volume is shown in Figures 1(a) and (b) for TlBr and TlCl respectively.
The results are also shown along with other theoretical values in Table 1. It is found that the generalized gradient approximation (GGA) gives quite nice values comparing to those obtained by other authors.
3.2. Optical Properties
The study of the optical constants and their variation with frequency is very interesting for the uses of films in optical applications. These applications require accurate knowledge of the optical constants over a wide wavelength range.
The reflectivity (R) of materials of refractive index (n) and extinction coefficient (k) is given by:
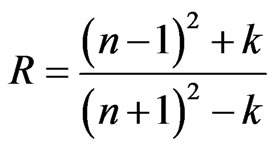 (8)
(8)
The spectra of all optical functions were calculated in the spectrum range 0 - 20 eV .
The dielectric functions of TlBr and TlCl in the cubic structure are resolved into one component εxy(ω), the average of the spectra for the polarization along the x and y-directions is given in Table 2.
 (a)
(a) (b)
(b)
Figure 1. (a) Energy (eV) versus volume (Å3) for TlBr; (b) energy (eV) versus volume (Å3) for TlCl.

Table 1. Static equilibrium constant a (Å) for TlBr and TlCl. comparison of present results with previous calculations.

Table 2. The calculated dielectric constants for TlBr and TlCl.
Figure 2 shows the variation of the dispersive part of the dielectric function, ε1. The calculated spectra have been obtained by Kramers-Kronig transformation of the shifted ε2 spectra. The main features for both compounds are a shoulder at lower energies, a rather steep decrease between 4.5 and 6.5 eV for TlBr and 6 to 7.5 eV for TlCl, after which ε1 becomes negative, a minimum and a slow increase toward zero at higher energies. The calculated dielectric constants compared with the experimental data and some other works are shown in Table 2.
Next, we consider the imaginary part of the electronic dielectric function for TlBr and TlCl respectively (see Figure 3), for radiation up to 20 eV. The calculated results are rigidly shifted upwards by 0.81 eV and 1.14 eV for TlBr and TlCl respectively. The main feature is a broad peak with a maximum around 6 eV for TlBr and 6.5 eV for TlCl, the maximum amplitude is at 13 for TlBr and 12 for TlCl, a shoulder is also visible at around 9 eV for TlBr and 10 eV for TlCl. The peak as well as the shoulders are excellently reproduced in the calculations, as are the general form of some experimental spectra [14]. There are also two other groups of peaks, in (9.3 - 12.2 eV) for TlBr and (8.2 - 12 eV) for TlCl photon energy range, they are mainly due to transitions in the vicinity of X and R.
Figure 4 shows the reflectivity spectra of T1Br and TlCl in the energy region below 20 eV. The spectra are consistent with the previous measurements [5,6]. The peaks at 5.1 eV and 6.4 eV for TlBr and TlCl respectively, are due to the lowest direct exciton transition at X point in the Brillouin zone, namely the excitonic transitions from the T1 + 5d core level to the 6p level. The structures below 13 eV are due to the transitions from the valence band composed of T1 + 6s states and halogen p states to the conduction band of mainly T1 ± 6p states.
The absorption spectra of TlBr and TlCl are displayed in Figure 5, they are very similar to the spectrum α(E) calculated using the experimental data [10].
The similarity of the coefficients of the absorption edge and exciton peaks in the TlBr and TlCl is evidence that the absorption edge in these salts is the tail of the first direct exciton peak.
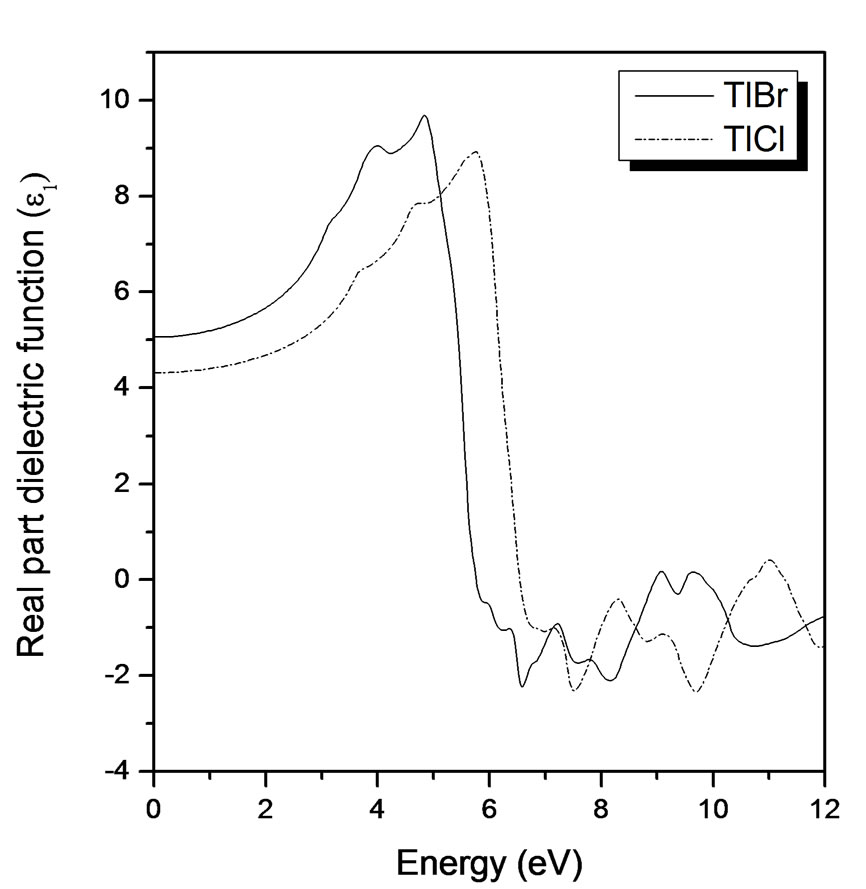
Figure 2. Real part of dielectric function versus energy (eV) for TlBr and TlCl.
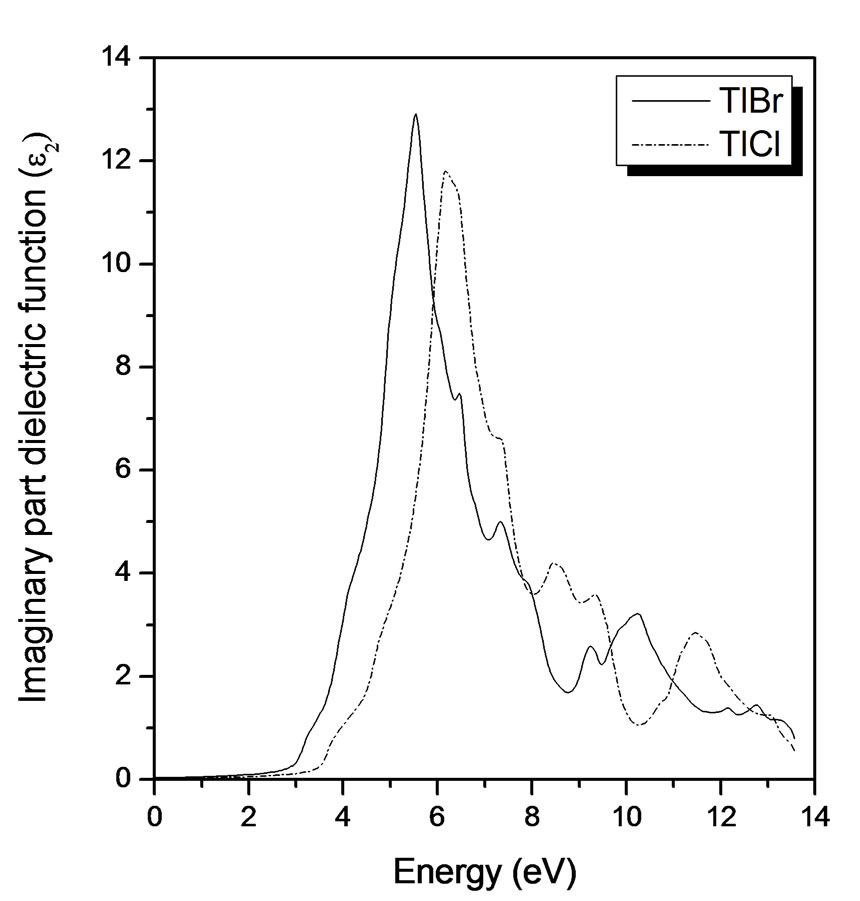
Figure 3. Imaginary part of dielectric function versus energy (eV) for TlBr and TlCl.

Figure 4. Reflectivity (R) versus energy (eV) for TlBr and TlCl.
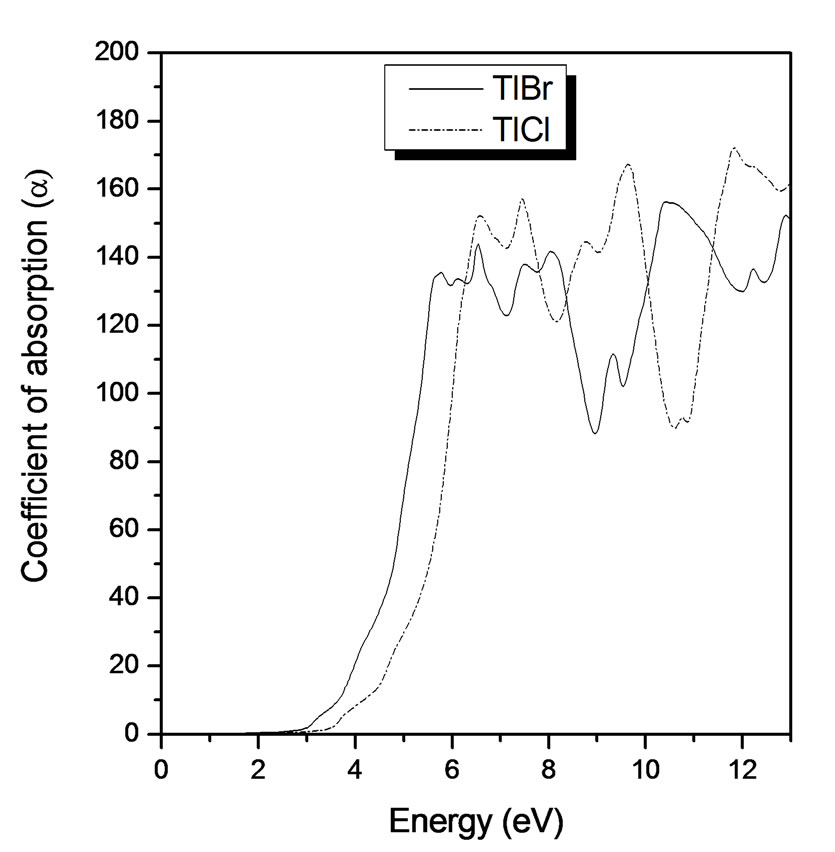
Figure 5. Absorption coefficient (α) versus energy (eV) for TlBr and TlCl.
The absorption and luminescence spectra of thallium halides reveal, at the fundamental edges, clearly pronounced exciton effects, namely, series of narrow exciton lines, which imply the existence of bound exciton– phonon states [31].
We now shortly discuss the spectra obtainable from the dielectric function, namely the refractive index.
As seen in Figure 6, the refractive indices for both TlBr and TlCl were computed using both real and imaginary parts of the dielectric function. It shows that the refractive index exhibits a significant dispersion in the short wavelength region were absorption is strong. It increases with the increase of the energy of the incident
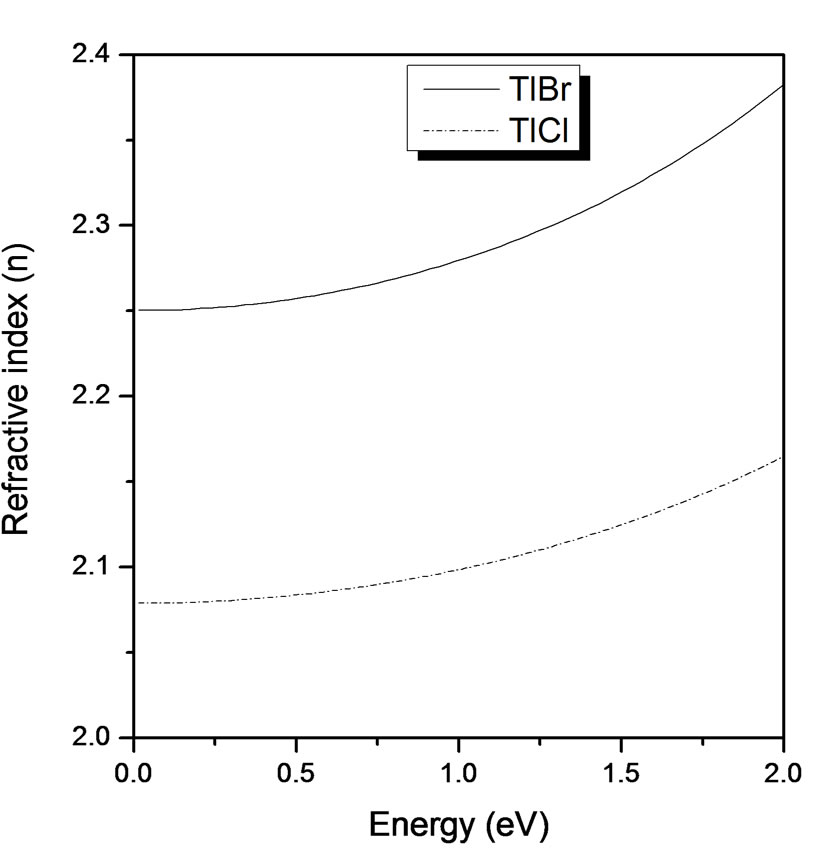
Figure 6. Refractive index (n) versus energy (eV) for TlBr and TlCl.
light, becoming nearly flat in the higher region. It is observed also that n reached a peak value at 2.39 eV for TlBr and 2.19 eV for TlCl, consistent with previous experimental measurements, and these peaks occurred more or less at the same energy in the real part of the dielectric constant energy dependence curves.
4. Conclusions
The optical properties of cubic TlBr and TlCl have been investigated using the wien2k package, full-potential linearized augmented plane wave (FP-LAPW) approach within the density functional theory (DFT) in the local spin density approximation (LSDA) including the generalized gradient approximation (GGA) was used. The use of GGA for the exchange-correlation potential permitted us to obtain good structural parameters. The real and imaginary parts of the dielectric functions were calculated for polarization in the x-y plane, the optical properties are excellently reproduced using the density functional theory, if we allow for a rigid shift of the band structure, the so-called scissors operator.
Thus, in this paper, all the optical spectra, and localization of transitions in the volume of the Brillouin zone are successfully calculated using the theoretical FLAPW method.
REFERENCES
- R. P. Singh, R. K. Singh and M. Rajagopalan, “Theoretical Investigations on Structural, Elastic and Electronic Properties of thallium halides,” Physica B: Condensed Matter, Vol. 406, No. 9, 2011, pp. 1717-1721.
- M.-H. Du, “First-Principles Study of Native Defects in TlBr: Carrier Trapping, Compensation, and Polarization Phenomenon,” Journal of Applied Physics, Vol. 108, No. 5, 2010, pp. 053506-053510.
- W. Zou and W. Liu, “Comprehensive ab Initio Calculation and Simulation on the Low-Lying Electronic States of TlX (X = F, Cl, Br, I, and At),” Journal of Computational Chemistry, Vol. 30, No. 4, 2009, pp. 524-539. doi:10.1002/jcc.21080
- M. Ueta, H. Kanzaki, K. Kobayashi, Y. Toyozawa and E. Hanamura, “Excitonic Processes in Solids,” Springer, Berlin, 1986.
- D. C. Hinson and J. R. Stevenson, “Optical Constants of TlCl and TlBr with a Comparison of the Kramers-Kronig and ‘Two-Angle’ Methods of Data Analysis,” Physical Review, Vol. 159, No. 3, 1967, pp. 711-716. doi:10.1103/PhysRev.159.711
- J. Kanamori and A. Kotani, “Core-Level Spectroscopy in Condensed Systems,” Springer, Berlin, 1988.
- V. F. Agekyan and Yu. A. Stepanov, “Optical and Structural Properties of Thallium Halide Microcrystals in a Porous Matrix,” Physics of the Solid State, Vol. 43, No. 4, 2001, pp. 763-765. doi:10.1134/1.1366007
- R. Clasen, “Non-Tetrahedrally Bonded Elements and Binary Compounds I,” Springer, Berlin, 1998.
- M. Gluyas, R. Hunter and B. W. James, “The Elastic Constants of Thallium Chloride in the Range 150 to 300 K,” Journal of Physics C: Solid State Physics, Vol. 8, No. 3, 1975, pp. 271-282.
- Sakuragi, et al., “IR Transmission Capabilities of Thallium Halide and Silver Halide Optical Fibers,” Adv. in Cerm., Vol. 2, 1981, pp. 84-93.
- J. Frandon and B. Lahaye, “Pertes Caractéristiques des Électrons dans TlCl, TlBr, Tl I et Calcul des Fonctions Optiques Entre 3 et 25 eV,” Journal de Physique, Vol. 33, No. 2-3, 1982, pp. 229-235. doi:10.1051/jphys:01972003302-3022900
- V. F. Agekyan and Yu. A. Stepanov, “Optical and Structural Properties of Thallium Halide Microcrystals in a Porous Matrix,” Physics of the Solid State, Vol. 43, No. 4, 2001, pp. 763-765. doi:10.1134/1.1366007
- M. O. Kolinko and O. V. Bovgyra, “Calculation of The Spectra of Characteristic Electron Losses in Indium Bromide,” Semiconductor Physics, Quantum Electronics & Optoelectronics, Vol. 10, No. 3, 2007, pp. 19-22.
- V. Yannopapas and A. Moroz, “Negative Refractive Index Metamaterials from Inherently Non-Magnetic Materials for Deep Infrared to Terahertz Frequency Ranges,” Journal of Physics: Condensed Matter, Vol. 17, No. 25, 2005, pp. 3717-3734. doi:10.1088/0953-8984/17/25/002
- K. Schwarz, P. Blaha and G. K. H. Madsen, “Proceedings of the Europhysics Conference on Computational Physics Computational Modeling and Simulation of Complex Systems,” Computer Physics Communications, Vol. 147, No. 1-2, 2002, pp. 71-76. doi:10.1016/S0010-4655(02)00206-0
- K. Schwarz and P. Blaha, “Proceedings of the Symposium on Software Development for Process and Materials Design,” Computational Materials Science, Vol. 28, No. 2, 2003, pp. 259-273. doi:10.1016/S0927-0256(03)00112-5
- D. M. Ceperley and B. I. Alder, “Ground State of the Electron Gas by a Stochastic Method,” Physical Review Letters, Vol. 45, No. 7, 1990, pp. 566-569. doi:10.1103/PhysRevLett.45.566
- E. Wimmer, H. Krakauer and M. Weinert, “Full-Potential Self-Consistent Linearized-Augmented-Plane-Wave Method for Calculating the Electronic Structure of Molecules and Surfaces: O2 Molecule,” Physical Review B, Vol. 24, No. 2, 1981, pp. 864-875. doi:10.1103/PhysRevB.24.864
- P. Blaha, K. Schwarz, P. Sorantin and S. B. Trikey, “Full-Potential, Linearized Augmented Plane Wave Programs for Crystalline Systems,” Computer Physics Communications, Vol. 59, No. 2, 1990, 399-415. doi:10.1016/0010-4655(90)90187-6
- O. K. Andersen, “Linear Methods in Band Theory,” Physical Review B, Vol. 12, No. 8, 1975, pp. 3060-3083. doi:10.1103/PhysRevB.12.3060
- D. Singh, “Ground-State Properties of Lanthanum: Treatment of Extended-Core States,” Physical Review B, Vol. 43, No. 8, 1991, pp. 6388-6392. doi:10.1103/PhysRevB.43.6388
- E. Sjöstedt, L. Nordström and D. J. Singh, “An Alternative Way of Linearizing the Augmented Plane-Wave Method,” Solid State Communications, Vol. 114, No. 1, 2000, pp. 15-20.
- P. Blaha, K. Schwarz, G. K. H. Madsen, D. Kvanicka and J. Luitz, “WIEN2k, an Augmented Plane Wave plus Local Orbitals Program for Calculating Crystal Properties,” Vienna University of Technology, Austria 2001.
- H. J. Monkhorst and D. Pack, “Special Points for Brillouin-Zone Integrations,” Physical Review B, Vol. 13, No. 12, 1976, pp. 5188-5192. doi:10.1103/PhysRevB.13.5188
- F. D. Murnaghan, “The Compressibility of Media under Extreme Pressures,” Proceedings of the National Academy of Sciences of the United States of America, Vol. 30, No. 9, 1944, pp. 244-247.
- M. A. Popova, T. J. Darvojda and M. A. Gurevich, “Thermochemistry of Some Refractory Compounds,” Zhurnal Neorganicheskoi Khimii, Vol. 11, 1966, pp. 1236-1238.
- Y. Fujii, T. Sakuma, J. Nakahara, S. Hoshino, K. Kobayashi and A. Fujii, “Neutron Scattering Study of Phonon Dispersion Relations along [110] in TlCl,” Journal of Physical Society of Japan, Vol. 44, 1978, pp. 1237-1240. doi:10.1143/JPSJ.44.1237
- J. P. van Dyke and G. A. Samara, “Thallous Halides: Pressure Dependence of the Energy-Band Structure and the Insulator-Metal Transition,” Physical Review B, Vol. 11, No. 12, 1975, pp. 4935-4944. doi:10.1103/PhysRevB.11.4935
- R. P. Lowndes, “Anharmonicity in the Silver and Thallium Halides: Far-Infrared Dielectric Response,” Physical Review B, Vol. 6, No. 4, 1972, pp. 1490-1498. doi:10.1103/PhysRevB.6.1490
- G. A. Samara, “Temperature and Pressure Dependence of the Dielectric Constants of the Thallous Halides,” Physical Review, Vol. 165, No. 3, 1968, pp. 959-969. doi:10.1103/PhysRev.165.959
- J. Nakahara, K. Kobayashi and A. Fujii, “Edge Absorption Stimulated by Disorder in Mixed Crystals of Thallous Halides,” Journal of Physical Society of Japan, Vol. 37, 1974, pp. 1319-1324. doi:10.1143/JPSJ.37.1319

