Atmospheric and Climate Sciences
Vol.06 No.04(2016), Article ID:71153,11 pages
10.4236/acs.2016.64039
Evaluation on Radar Reflectivity-Rainfall Rate (Z-R) Relationships for Guyana
Komalchand Dhiram1,2, Zhenhui Wang2,3
1Hydrometeorological Service, Ministry of Agriculture, Georgetown, Guyana
2Collaborative Innovation Center on Forecast and Evaluation of Meteorological Disasters, CMA Key Laboratory for Aerosol-Cloud-Precipitation, Nanjing University of Information Science & Technology, Nanjing, China
3School of Atmospheric Physics, Nanjing University of Information Science & Technology, Nanjing, China

Copyright © 2016 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY-NC).
http://creativecommons.org/licenses/by-nc/4.0/



Received: August 6, 2016; Accepted: October 8, 2016; Published: October 11, 2016
ABSTRACT
The constant development of science and technology in weather radar results in high-resolution spatial and temporal rainfall estimates and improved early warnings of meteorological phenomena such as flood [1] . Weather radars do not measure the rainfall amount directly, so a relationship between the reflectivity (Z) and rainfall rate (R), called the Z-R relationship (Z = aRb), where a and b are empirical constants, can be used to estimate the rainfall amount. In this research, mathematical techniques were used to find the best climatological Z-R relationships for the Low Coastal Plain of Guyana. The reflectivity data from the S-Band Doppler Weather Radar for February 17 and 21, 2011 and May 8, 2012 together with the daily rainfall depths at 29 rainfall stations located within a 150 km radius were investigated. A climatological Z-R relationship type Z = 200R1.6 (Marshall-Palmer) configured by default into the radar system was used to investigate the correlation between the radar reflectivity and the rainfall by gauges. The same data sets were used with two distinct experimental Z-R relationships, Z = 300R1.4 (WSR-88D Convective) and Z = 250R1.2 (Rosenfeld Tropical) to determine if any could be applicable for area of study. By comprehensive regression analysis, New Z-R and R-Z relationships for each of the three events aforementioned were developed. In addition, a combination of all the samples for all three events were used to produce another relationship called “All in One”. Statistical measures were then applied to detect BIAS and Error STD in order to produce more evidence-based results. It is proven that different Z-R relationships could be calibrated into the radar system to provide more accurate rainfall estimation.
Keywords:
Radar Reflectivity, Rain Gauges, Rainfall Rate, Z-R Relationships, Correlation

1. Introduction
High accuracy of rainfall estimation is required for better decisions by policy makers and researchers. The rain gauge has been the standardized instrument for collecting and measuring surface rainfall and is assumed to be “ground truth” because of its long service and widespread use [2] . Nevertheless, rain gauges produce point measurements that are commonly assumed to represent a much wider surface area.
Rain gauges are reliable instruments which meteorologists and hydrologists can rely on at least for point measurement [3] , but rainfall can vary both in space and time which is not really captured by the rain gauges. Thus, there have been considerable interests in utilizing the weather radar, since it provides spatially and temporally continuous measurements that are immediately available at the radar site [4] [5] . But the fundamental feature of weather radars is that they do not measure rainfall directly but rather the back scattered energy from precipitation particles from elevated volumes and an algorithm should be developed and calibrated against the rain gauge network. The received energy from the precipitation particles is given by:
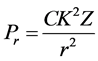 (1)
(1)
where, C = radar constant, K = imaginary dielectric constant, r = range of the target and Z = radar reflectivity factor.
As the weather radar does not measure rainfall rates directly, it is prone to errors from different sources. The three major sources of errors associated with radar estimates are [4] : the variations in the relationship between the backscattered energy and rainfall rates, changes in precipitation forms before reaching the ground, and anomalous propagation of beams.
Guyana’s climatological network consists of approximately 182 daily rainfall recording stations. Distances between stations are not distributed evenly and there is none in certain areas, which leads to insufficient spatial sampling. In addition, wind/turbulent losses, gauge wetting, splash into and out of the gauge and evaporation compound the estimation problem which increases measurement errors [6] - [9] . A recently installed Doppler Weather Radar (DWR)-S band attempts to solve these problems by providing a temporally continuous spatial estimate of rainfall. The DWR precipitation processing system brings a dramatic advancement to operational radar estimated precipitation in Guyana.
This research uses regression analyses to compare the relationship between the rain gauge rainfall and radar reflectivity rain rate, and to use an optimization approach to find suitable climatological Z-R relationships for the Low Coastal Plain of Guyana. The reflectivity data from the S-Band DWR together with the daily rainfall depths at 29 rainfall stations located within a 150 km radius were analyzed.
2. Data
Monthly weather summaries produced by the Hydrometeorological Service of Guyana were analyzed with the hope to determine extreme/special events. During the process of data collection most of the radar data for special events were inaccessible and for those available there were missing reflectivity within a daily set which was a major setback in this research. In addition, the data set for the rain gauges is only available in mm per day (daily rainfall). After careful consideration, February 17 and 21, 2011, and May 8, 2012 were selected for analysis. No extensive quality control was needed for the rain gauge data as this would have already been done by comparative analyses with climatological normal and in some cases data from automatic weather stations before they could be used in the Monthly Weather Summary.
The Plan Position Indicator (PPI), a standard product, is the most common type of radar display. Generally, the antenna sends pulses while rotating 360 degrees around the radar site at fixed elevation. The same antenna receives the return echoes. It is processed by the receiver and the display of the data can be seen on the Constant Altitude Plan Position Indicator (CAPPI). The CAPPI was used because of its characteristics to display images of high quality resolution which can be easily analyzed; an example of such image can be seen below in Figure 1(a). Figure 1(b) below shows the rain fall stations within the radar scan range of 150 km. Due to blank data and incorrect coordinates some stations could not be used. The rain gauge data are recorded as daily rainfall total and was measured by semi qualified persons or Part-Time Observers.
3. Methodology
The total amount of rainfall for a selected period is expressed as the depth of water which would cover a horizontal area (m2) if there is no runoff, infiltration or evaporation. This depth is generally expressed in millimeters and is the rainfall depth [10] . Rain gauge measurements, although representing only point rainfall, are very often considered the “ground truth” rainfall although there are some errors still associated with it. In this study, a simple measuring cylinder is being used to take rainfall measurements.
As mentioned earlier, a radar does not directly measure rainfall totals, but estimate rainfall rate, R (mm/h), by an empirical relationship with the radar reflectivity factor, Z (mm6/m3). Rainfall rates are proportional to the volume of the raindrops, but reflectivity is proportional to sixth-power of the drop diameter [11] . Therefore, a raindrop size distribution must be assumed to convert from reflectivity to rainfall rate. Reflectivity is converted into a rainfall rate by the Z-R relationship using the formula:
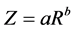 (2)
(2)
where a and b are constants. A significant problem is that the Z-R relationship values vary as a function of precipitation types because of the differences in raindrop size distributions [12] . Additional factors complicating the Z-R relationship include: beam attenuation [2] and [9] , range effects [2] , hail and vertical air motions [9] .
The Rainbow software [13] is the most comprehensive and versatile software system available today for weather radar data processing and was used to process the radar raw data for this research.


Figure 1. Sample of a CAPPI radar reflectivity image (a) and location of rain gauges (b).
3.1. Consideration for Quality Control
Height sampling errors are caused by the bright band that results in a range dependent bias [14] - [19] . The so called Bright Band is a thin horizontal layer of enhanced reflectivity (typically 5 to 10 dBZ higher than for the neighbored layers) because of melting ice particles. It is usually well-exhibited in stratiform precipitation, and causes errors in rainfall estimates if not treated properly. The Bright Band is corrected by an algorithm in the Rainbow tool. It works on corrected reflectivity raw data (dBZ). The polar raw data volume is processed by similar technique described by [20] .
Ground clutters are non-precipitation radar echoes that are produced when the main or side lobes of radar beam hit other targets such as buildings, mountains and trees. The backscattered radar signals from those objects result in robust radar reflectivity resulting to an overestimation of the radar rainfall. Increasing the elevation angle of the radar beam could significantly reduce any ground clutters [21] . Nevertheless, this strategy may cause increases in height sampling error [22] . Within the 150 km range selected for this research there is no such buildings, mountains or trees higher than the radar’s lowest elevation scan, therefore, ground clutters were not considered in this research.
Atmospheric gases in the clear atmosphere contribute towards attenuation of radar power transmitted into the atmosphere. Oxygen and water vapour are the main atmospheric gases that need to be considered as absorbers [23] . Attenuation caused by cloud and rain vary strongly according to cloud parameters and rainfall rate [22] . As the precipitation intensity can be derived from the reflectivity as mentioned earlier and similar relations between the rain intensity R (in mm/hour or mm/day) and the specific two-way attenuation (dB/km) [23] , the measured reflectivity data can be used to calculate the specific attenuation and thus to correct the reflectivity data. However, it depends on the wavelength. The significance of attenuation correction for S-band is usually negligible as compared to X-band and therefore the attenuation correction was not considered in this study because the reflectivity data used are from an S-band radar.
Further, there is no unique relationship between radar reflectivity and the rainfall rate since the relationship depends on the particle size distribution. Also, the natural variability in drop-size distributions is an important source of uncertainty in radar rainfall measurements when other factors are taken into account. So since there was no desdrometer data available, no analysis on the mass content and fall velocity was considered in this research and therefore the method proposed by [14] , the rainfall field is assumed to remain stationary in space and intensity during the sampling interval was applied.
3.2. Climatological Z-R Relationships
The following Table 1 contains the three standard Z-R relationships used for radar reflectivity conversion in this research.
3.3. Selection of Radar Reflectivity Images and Conversion
The Rainbow software generates CAPPI images with a radius of 150, 250, or 400 km on a 15 min interval. These are images that were produced from a PPI algorithm which starts with a volume dataset and consists of reflectivity (dBZ), Velocity (V) and Spectral
Table 1. The Z-R relationships that were used in this research.
width (W). From the PPI algorithm all vertical fall speed of particles would have been subtracted by a configuration done in the Rainbow software. The CAPPI imagery with a radius of 150 km was selected for analysis because the rain gauges used in this research are all located within this range.
The algorithm performed for the conversion is as follow:
1) The first 15 min image of 00:00 hour (Coordinate Universal Time) was used to start the counting of images for each day (i.e. 24 hours) because the rain gauge measurement is taken at Coordinates Universal Time. Then all pixels that were considered as zero reflectivity, or noise and clutters (less than 15 dBZ and more than 53 dBZ) were eliminated [24] .
2) Noting that the rain gauge rainfall is in mm per day and by using the default Z-R relationship (Z = 200R1.6), the conversion techniques proposed by [25] and [26] were applied to the radar reflectivity. The instantaneous reflectivity values are converted in to radar rain rates and then accumulated into daily radar rainfall. This conversion was performed for the WSR-88D and Rosenfeld Tropical relationships and for the rest of rain events.
3) Logarithmic operations were performed on the gauge rainfall (x = log(R)) and the radar reflectivity (y = log(Z)). From the results obtained a regression analysis is done to determine the values of the constants a and b which is used for the new Z-R and R-Z relationships. This step is repeated for all three events. Many researchers recommend that parameter b does not need to be varied as much as the parameter a. The values of a and b were found to be within the ranges of 31 - 500 and 1.1 - 1.9, respectively [22] .
According to [27] , the following three quantities are used to estimate the difference between the mean radar rainfall ( ) and mean gauge rainfall (
) and mean gauge rainfall ( ).
).
Root Mean-Square Error,
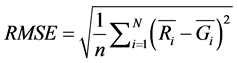 (3)
(3)
BIAS,
 (4)
(4)
Error Standard Deviation,
 (5)
(5)
4. Results and Discussion
A summary for all the results obtained can be seen in Table 2 below. The first column shows the rain events, while the second column contains the sample size or number of stations used for the analyses. The third column shows the new constants of a and b that were derived from the same data sets used in this research; additionally, from these constants new Z-R (R1) and R-Z relationships (R2) were derived for each event. The fourth column contains the statistical measures used, where the BIAS and Error STD were calculated as per Equations 4 and 5 respectively, and the correlation factor (R2) were determined from regression analyses. The rows for the remainder of columns are values obtained from rows in the fourth column for the different relationships.
With respect to regression analysis, results show good correlation between rain gauge observation and radar estimations for all relationships, however, R2 is considered the best according to both BIAS and Error STD. This must be because R2 is based on R-Z regression equation. MP is slightly worse than R2 but better than the rest according to the values of STD. This might imply that the precipitation characteristics are in consistency with MP hypothesis and the events selected were all stratiform, though, due to geographical location, convective type of precipitation would mostly be expected. Daily register forms and synoptic analyses generalized the atmospheric conditions for the events as surges of oscillated moisture producing widespread cloudy condition. In addition, synoptic recordings at some locations confirm that the clouds types and classification for these three events would have produced stratiform precipitation. There was little convection in some areas but its proportion to stratiform was minimal which further provide reasons why MP seems to be the best suited Z-R relationship for data used in this research. Both WSR-88D and RT are not good for Guyana according to the re- sults in Table 2 and scatter plots as per Figure 2 below. The event considered as “All in
Table 2. Statistical summary of results obtained.






Figure 2. Scatter plots between radar estimated and gauge observed rainfall for the 3 events are in the 3 lines (a)-(c) for Marshall-Palmer, WSR-88D and Rosenfeld, respectively, and (d) and (e) for R1 and R2.
One” is a summation of all samples for all three events where only R2 shows good values.
As per results above, both theoretically and practically, such good correlation factors (R2) are considered too perfect or in some cases impractical. It should be noted that these values were achieved because the regression analyses were done on daily samples. Should the case be hourly rain rates then R2 may vary depending on the precipitation type, Z-R relationships, topography and other factors.
The Bias and Standard Deviation have proven how often the use of only regression analysis could lead to misconception when comparison is being done for the investigation of the best suited Z-R relationships.
5. Conclusions and Recommendations
This research evaluated the most suitable Z-R relationships for Guyana. It is therefore worthwhile to conclude that the use of Marshall-Palmer and WSR-88D relationships have both demonstrated good results, however, R1 and R2, which are newly derived relationships from this research, have produced better. Though, the accepted values for the components of the Z-R equation, a and b, should fall between the range of 31 - 500 and 1.1 - 1.9, respectively. The a components derived from this research fall outside of the recommended range for all the events while the b fits well.
The results show that it is possible for different Z-R relationships to be calibrated into the radar system which could improve the rainfall estimations. With this being said, it is also noted that an increase in number of rain gauges/radar reflectivity rain rates pairs, decrease in data collection interval from mm/daily to mm/hour, and selection of events with different synoptic conditions could provide interesting results and conclusions of whether or not the Z-R relationships should be varied in the radar system according to the climatic seasons in Guyana.
Guyana has recently installed approximately 20 automatic weather stations (hydrometeorological). The interval of rainfall data collection for these stations can be adjusted to suit that of the radar rainfall reflectivity which could open the doors for parallel method of Z-R relationships evaluation. In addition, precipitation products from Numerical Models such as WRF should also be considered for radar product evaluation. All outcomes from this research will be considered for future configuration and calibration of the radar system in Guyana and specifically those that are positive will be put into immediate effect. This is the first time a Z-R relationship research has been carried out on Guyana’s Doppler Weather Radar and as such, it could be used as a guidance to perform future research on rainfall estimation both locally and within the region.
Acknowledgements
Financial support from China Commonwealth Industry Research Project (GYHY201306078) and the National Natural Science Foundation of China (41275043) is acknowledged. Thanks to work of Prof. Zhang Peichang of Nanjing University of Information Science & Technology translated orally to me by Prof. Wang Zhenhui which has provided guidance towards this research. Many thanks for the support from the Hydrometeorological Service, Ministry of Agriculture, Guyana.
Cite this paper
Dhiram, K. and Wang, Z.H. (2016) Evaluation on Radar Reflectivity-Rainfall Rate (Z-R) Relationships for Guyana. Atmospheric and Climate Sciences, 6, 489-499. http://dx.doi.org/10.4236/acs.2016.64039
References
- 1. Meischner, P. (2004) Weather Radar: Principles and Advanced Applications. Springer-Verlag, Berlin, Heidelberg, 337 p.
http://dx.doi.org/10.1007/978-3-662-05202-0 - 2. Hunter, S. (1996) WSR-88D Radar Rainfall Estimation: Capabilities, Limitations and Potential Improvements. National Weather Digest, 20, 26-38.
- 3. Moreau, E., Testud, J. and Le Bouar, E. (2009) Rainfall Spatial Variability Observed by X-Band Weather Radar and Its Implication for the Accuracy of Rainfall Estimates. Advances in Water Resources, 32, 1011-1019.
http://dx.doi.org/10.1016/j.advwatres.2008.11.007 - 4. Wilson, J.W. and Brandes, E.A. (1979) Radar Measurement of Rainfall: A Summary. Bulletin of the American Meteorological Society, 60, 1048-1058.
http://dx.doi.org/10.1175/1520-0477(1979)060<1048:RMORS>2.0.CO;2 - 5. Einfalt, T., Nielsen, K.A., Golz, C., Jensen N.E., Quirmbach, M., Vaes, G. and Vieux, B. (2004) Towards a Roadmap for Use of Radar Rainfall Data in Urban Drainage. Journal of Hydrology, 299, 186-202.
http://dx.doi.org/10.1016/S0022-1694(04)00365-8 - 6. Yang, D., Goodison, B., Metcalfe, J., Golubev, V., Bates, R., Pangburn, T. and Hanson, C. (1998) “Accuracy of NWS 8” Standard Non-Recording Precipitation Gauge: Results and Application of WMO Inter-Comparison. Journal of Atmospheric and Oceanic Technology, 15, 54-67.
http://dx.doi.org/10.1175/1520-0426(1998)015<0054:AONSNP>2.0.CO;2 - 7. Groisman, P. and Legates, D. (1994) The Accuracy of United States Precipitation Data. Bulletin of the American Meteorological Society, 75, 215-227.
http://dx.doi.org/10.1175/1520-0477(1994)075<0215:TAOUSP>2.0.CO;2 - 8. Brandes, E. and Wilson, J. (1988) Measuring Storm Rainfall by Radar and Rain Gauge. In: Kessler, E., Ed., Instruments and Techniques for Thunderstorm Observation and Analysis, University of Oklahoma Press, Norman, 171-186.
- 9. Austin, P.M. (1987) Relation between Measured Radar Reflectivity and Surface Rainfall. Monthly Weather Review, 115, 1053-1071.
http://dx.doi.org/10.1175/1520-0493(1987)115<1053:RBMRRA>2.0.CO;2 - 10. (1998) Annex II: Rainfall Measurement. FAO Irrigation and Drainage Paper 27, Agrometeorological Field Stations, Chapter 6.
http://www.fao.org/docrep/t7202e/t7202e09.htm - 11. Burgess, D.W. and Ray, P.S. (1986) Principles of the Radar. In: Ray, P., Ed., Mesoscale Meteorology and Forecasting, American Meteorological Society, Boston, 85-117.
- 12. Joss, J. and Lee, R. (1995) The Application of Radar-Gauge Comparisons to Operational Precipitation Profile Corrections. Journal of Applied Meteorology, 34, 2612-2630.
http://dx.doi.org/10.1175/1520-0450(1995)034<2612:TAORCT>2.0.CO;2 - 13. Selex ES Gmbh-Finmeccanica Company (2015).
http://www.de.selex-es.com/capabilities/meteorology/products/components/rainbow5 - 14. Fabry, F., Bellon, A., Duncan, M.R., Austin, G.L. (1994) High Resolution Rainfall Measurements by Radar for Very Small Basins: The Sampling Problem Re-Examined. Journal of Hydrology, 116, 415-28.
http://dx.doi.org/10.1016/0022-1694(94)90138-4 - 15. Kitchen, M., Brown. R. and Davies, A.G. (1994) Real-Time Correction of Weather Radar for the Effects of Bright Band, Range and Orographic Growth in Widespread Precipitation. Quarterly Journal of the Royal Meteorological Society, 120, 1231-1254.
http://dx.doi.org/10.1002/qj.49712051906 - 16. Andrieu, H. and Creutin, J.D. (1995) Identification of Vertical Profiles of Radar Reflectivity for Hydrological Applications Using an Inverse Method. Part I: Formulation. Journal of Applied Meteorology, 34, 225-239.
http://dx.doi.org/10.1175/1520-0450(1995)034<0225:IOVPOR>2.0.CO;2 - 17. Fabry, F. and Zawadzki, I. (1995) Long-Term Radar Observations of the Melting Layer of Precipitation and Their Interpretation. Journal of the Atmospheric Sciences, 52, 838-861.
http://dx.doi.org/10.1175/1520-0469(1995)052<0838:LTROOT>2.0.CO;2 - 18. Vignal, B. and Andrieu, H. (1999) Identification of Vertical Profiles of Reflectivity from Volume Scan Radar. Journal of Applied Meteorology, 38, 1214-1228.
http://dx.doi.org/10.1175/1520-0450(1999)038<1214:IOVPOR>2.0.CO;2 - 19. Vignal, B. and Krajewski, W.F. (2001) Large-Sample Evaluation of Two Methods to Correct Range-Dependent Error for WSR-88D Rainfall Estimates. Journal of Hydrometeorology, 2, 490-504.
http://dx.doi.org/10.1175/1525-7541(2001)002<0490:LSEOTM>2.0.CO;2 - 20. Smith, C.J. (1986) The Reduction of Errors Caused by Bright Bands in Quantitative Rainfall Measurements Made Using Radar. Journal of Atmospheric and Oceanic Technology, 3, 129-141.
http://dx.doi.org/10.1175/1520-0426(1986)003<0129:TROECB>2.0.CO;2 - 21. Gabella, M. and Perona, G. (1998) Simulation of the Orographic Influence on Weather Radar Using Geometric-Optics Approach. Journal of Atmospheric and Oceanic Technology, 15, 1485-1494.
http://dx.doi.org/10.1175/1520-0426(1998)015<1485:SOTOIO>2.0.CO;2 - 22. Chumchean, S. (2004) Improved Estimation of Radar Rainfall for Use in Hydrological Modelling. PhD Thesis, University of New South Wales, Sydney.
- 23. Battan, L.J. (1973) Radar Observation of the Atmosphere. University of Chicago Press, Chicago.
- 24. Fulton, R.A., Breidenbach, J.P., Seo, D.J., Miller, D.A. and O’ Brannon, T. (1998) The WSD-88D Rainfall Algorithm. Weather Forecasting, 13, 377-395.
http://dx.doi.org/10.1175/1520-0434(1998)013<0377:TWRA>2.0.CO;2 - 25. Seed, A.W., Sirivardena, L., Sun, X., Jordan, P. and Elliott, J. (2002) On the Calibration of Australian Weather Radars, Cooperative Research Centre for Catchment Hydrology. Technical Report 02/7, Melbourne, 40.
- 26. Fields, G., Seed, A., Yu, B. and Malone, T. (2004) Calibration of Weather Radar in South East Queensland. 6th International Symposium on Hydrological Applications of Weather Radar, Melbourne, 2-4 February 2004, 21.
- 27. Seed, A.W., Nicol, J., Austin, G.L., Stow, C.D. and Bradley, S.G. (1996) The Impact of Radar and Raingauge Sampling Errors When Calibrating a Weather Radar. Meteorological Applications, 3, 43-52.
http://dx.doi.org/10.1002/met.5060030105











