International Journal of Astronomy and Astrophysics
Vol.07 No.01(2017), Article ID:73973,17 pages
10.4236/ijaa.2017.71002
Study of Baryon Acoustic Oscillations with SDSS DR13 Data and Measurements of 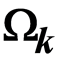 and
and 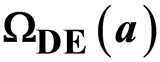
B. Hoeneisen
Universidad San Francisco de Quito, Quito, Ecuador

Copyright © 2017 by author and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY 4.0).
http://creativecommons.org/licenses/by/4.0/



Received: December 14, 2016; Accepted: February 4, 2017; Published: February 7, 2017
ABSTRACT
We measure the baryon acoustic oscillation (BAO) observables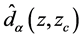 ,
,  , and
, and 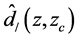 as a function of red shift
as a function of red shift  in the range 0.1 to 0.7 with Sloan Digital Sky Survey (SDSS) data release DR13. These observables are independent and satisfy a consistency relation that provides discrimination against miss-fits due to background fluctuations. From these measurements and the correlation angle
in the range 0.1 to 0.7 with Sloan Digital Sky Survey (SDSS) data release DR13. These observables are independent and satisfy a consistency relation that provides discrimination against miss-fits due to background fluctuations. From these measurements and the correlation angle  of fluctuations of the Cosmic Microwave Background (CMB), we obtain
of fluctuations of the Cosmic Microwave Background (CMB), we obtain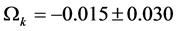 ,
, 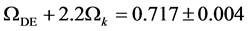 and
and 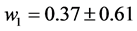 for dark energy density allowed to vary as
for dark energy density allowed to vary as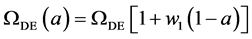 . We present measurements of
. We present measurements of 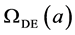 at six values of the expansion parameter
at six values of the expansion parameter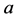 . Fits with several scenarios and data sets are presented. The data is consistent with space curvature parameter
. Fits with several scenarios and data sets are presented. The data is consistent with space curvature parameter 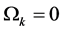 and
and 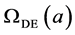 constant.
constant.
Keywords:
Cosmology, Dark Energy, Baryon Acoustic Oscillations

1. Introduction
Peaks in the density of the primordial universe are the sources of acoustic waves of the tightly coupled plasma of photons, electrons, protons and helium nuclei. These acoustic waves propagate a distance 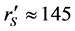 Mpc until the time of recombination and decoupling
Mpc until the time of recombination and decoupling 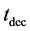 [1] [2] (All distances in this article are co-moving, i.e. are referred to the present time
[1] [2] (All distances in this article are co-moving, i.e. are referred to the present time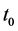 ). The baryon acoustic oscillation (BAO) distance
). The baryon acoustic oscillation (BAO) distance 











In this article, we present studies of BAO with Sloan Digital Sky Survey (SDSS) publicly released data DR13 [7] . The study has three parts:
1) We measure the BAO observables




2) We measure the space curvature parameter 











3) Finally, we use the BAO measurements as a calibrated standard ruler to constrain a wider set of cosmological parameters.
The present analysis with DR13 data [7] closely follows the methods developed in References [8] and [12] for data release DR12 [13] .
2. BAO Observables
To define the quantities being measured we write the (generalized) Friedmann equation that describes the expansion history of a homogeneous universe:

The expansion parameter 





The terms under the square root in Equation (1) are densities relative to the critical density of, respectively, non-relativistic matter, ultra-relativistic radiation, dark energy (whatever it is), and space curvature. In the General Theory of Relativity 








The distance 















We find the following approximations to 





Our strategy is as follows. We consider galaxies with redshift in a given range





・ If 





・ If 






・ Else, fill a third histogram of 

Note that these three histograms have different galaxy pairs, i.e. have inde- pendent signals and independent backgrounds.
The galaxy-galaxy correlation distance







A numerical analysis obtains 
















The independent BAO observables



The approximations in Equations (4) obtain galaxy-galaxy correlation distances



The BAO observables





It is observed that fluctuations in the CMB have a correlation angle [2] [9] .

(we have chosen a measurement by the Planck collaboration with no input from BAO). The extreme precision with which 




For 


3. Galaxy Selection and Data Analysis
The present analysis is based on publicly released SDSS-IV DR13 data described in Reference [7] , and includes the SDSS-III Baryon Oscillation Spectroscopic Survey (BOSS) [15] , and the SDSS-IV Extended Baryon Oscillation Spectroscopic Survey (eBOSS) [16] which are designed for BAO measurements. A list of participating institutions in the SDSS-IV is given in the acknowledgment.
We obtain the following data from the SDSS DR13 catalog [7] for all objects identified as galaxies that pass quality selection flags: right ascension ra, declination dec, redshift








We calculate the absolute luminosity 







A “run” is defined by a range of redshifts






Histograms are filled with weights 







Figure 1. Fits to histograms of 




The fitting function is a second degree polynomial for the background and, for the BAO signal, a step-up-step-down function of the form
where
A run is defined as “successful” if the fits to all three histograms converge with a signal-to-background ratio significance greater than 1 standard deviation (raising this cut further obtains little improvement due to the cosmological fluctuations of the background), and the consistency parameter Q is in the range 0.97 to 1.03 (if Q is outside of this range then at least one of the fits has converged on a fluctuation of the background instead of the BAO signal). We obtain 13 successful runs for N and 12 successful runs for S which are presented in Table 1 and Table 2 respectively. The histogram of the consistency parameter Q for these 25 runs is presented in Figure 1.
For each bin of redshift 

Table 1. Measured BAO distances








Table 2. Measured BAO distances








4. Uncertainties
Histograms of BAO distances 
Table 3. Independent measured BAO distances









each entry in Table 3. We present several estimates of the total uncertainties of the entries in Tables 1-3 extracted directly from the fluctuations of the numbers in these tables. All uncertainties in this article are at 68% confidence level.
We neglect the variation of







The 18 entries in Table 3 are independent. The r.m.s. differences for rows 1 - 2, 3 - 4 and 5 - 6 divided by 



The average and standard deviation of the columns


The r.m.s. of 







From these estimates, we take the following independent total uncertainties for each entry of


5. Corrections
Let us consider corrections to the BAO distances due to peculiar velocities and peculiar displacements of galaxies towards their centers. A relative peculiar velocity 







We multiply the measured BAO distances















The effect of these corrections can be seen by comparing the first two fits in Table 4 below. An order-of-magnitude estimate of this correction can be obtained by calculating the r.m.s. 



6. Measurements of 

We consider five scenarios:
1) The observed acceleration of the expansion of the universe is due to the cosmological constant, i.e. 
2) The observed acceleration of the expansion of the universe is due to a gas of negative pressure with an equation of state





can be integrated with the result [3] [17] [18]

If 


3) Same as Scenario 2 with 

Table 4. Cosmological parameters obtained from the 18 independent BAO measurements in Table 3 in several scenarios. Corrections for peculiar motions are given by Equation (11) except, for comparison, the fit “1*” which has no correction. Scenario 1 has 


4) We assume
5) 

Note that BAO measurements can constrain 



Let us try to understand qualitatively how the BAO distance measurements presented in Table 3 constrain the cosmological parameters. In the limit 















In Table 4, we present the cosmological parameters obtained by minimizing the 













In Table 5 we present the cosmological parameters obtained by minimizing the 




when 
Table 5. Cosmological parameters obtained from the 18 BAO measurements in Table 3 plus 




the data and the case 



We now add BAO measurements with SDSS BOSS DR11 data of quasar Ly




From the 18 BAO plus 
















7. Detailed Measurement of
We obtain 




Figure 2. Measurements of 











line corresponding to the central values of 


8. Measurements of


Up to this point, we have used the BAO distance 









The sound horizon is calculated from first principles [1] as follows:

where the speed of sound is

We can write the result for our purposes as

where

Figure 3. Same as Figure 2 for offset bins of 

(we have neglected the dependence of 
In this paragraph we take 



















In this paragraph we let 
























9. Comparison with Previous Measurements
Let us compare the results obtained with SDSS DR13 data with DR12 data. The 

Table 6. Cosmological parameters obtained from the 18 BAO measurements in Table 3 plus 





converging on background fluctuations instead of the BAO signal:





We compare Equation (14) for DR13 data, with the corresponding fits for DR12 data. From Table VIII of Reference [8] :

From Table VII of Reference [12] :

Note in Equation (14) how the DR13 data has lowered the uncertainties.
The final consensus measurements of the SDSS-III Baryon Oscillation Spectroscopic Survey [20] (an analysis of the DR12 galaxy sample), are presented in Table 7 (reproduced from Reference [12] for completness). There is agreement with the measurements of DR13 data in Table 3. The notation of Reference [20] is related to the notation of the present article as follows:


where 

10. Conclusions
1) The main results of these studies are the independent measured BAO observables




Table 7. Final consensus “BAO + FS” measurements of the SDSS DR12 data set [20] (uncertainties are statistical and systematic), and the corresponding BAO parameters 


[12] for DR12 data.
2) From the 18 BAO measurements in Table 3, and no other input, we obtain

for 






3) From 18 BAO measurements plus 

for 






4) Detailed measurements of 
5) From 18 BAO plus 


when 






For 







6) From 18 BAO plus 






7) For all data sets, we obtain no tension with the constraints 

The SDSS has brought the measurements of 

Acknowledgements
Funding for the Sloan Digital Sky Survey IV has been provided by the Alfred P. Sloan Foundation, the US Department of Energy Office of Science, and the Participating Institutions. SDSS-IV acknowledges support and resources from the Center for High-Performance Computing at the University of Utah. The SDSS web site is www.sdss.org.
SDSS-IV is managed by the Astrophysical Research Consortium for the Participating Institutions of the SDSS Collaboration including the Brazilian Participation Group, the Carnegie Institution for Science, Carnegie Mellon University, the Chilean Participation Group, the French Participation Group, Harvard- Smithsonian Center for Astrophysics, Instituto de Astrofísica de Canarias, The Johns Hopkins University, Kavli Institute for the Physics and Mathematics of the Universe (IPMU)/University of Tokyo, Lawrence Berkeley National Laboratory, Leibniz Institut für Astrophysik Potsdam (AIP), Max-Planck-Institut für Astronomie (MPIA Heidelberg), Max-Planck-Institut für Astrophysik (MPA Garching), Max-Planck-Institut für Extraterrestrische Physik (MPE), National Astronomical Observatories of China, New Mexico State University, New York University, University of Notre Dame, Observatário Nacional/MCTI, The Ohio State University, Pennsylvania State University, Shanghai Astronomical Observatory, United Kingdom Participation Group, Universidad Nacional Autónoma de México, University of Arizona, University of Colorado Boulder, University of Oxford, University of Portsmouth, University of Utah, University of Virginia, University of Washington, University of Wisconsin, Vanderbilt University, and Yale University.
Cite this paper
Hoeneisen, B. (2017) Study of Baryon Acoustic Oscillations with SDSS DR13 Data and Measurements of and International Journal of Astronomy and Astrophysics, 7, 11-27. https://doi.org/10.4236/ijaa.2017.71002
References
- 1. Eisenstein, D.J., Seo, H.-J. and White, M. (2007) On the Robustness of the Acoustic Scale in the Low-Redshift Clustering of Matter. The Astrophysical Journal, 664, 660-674.
https://doi.org/10.1086/518755 - 2. Patrignani, C., et al. (2016) Review of Particle Physics. Chinese Physics C, 40, Article ID: 100001.
https://doi.org/10.1088/1674-1137/40/10/100001 - 3. Bruce, A. (2009) Bassett and Renée Hlozek. arXiv:0910.5224
- 4. Weinberg, D.H., et al. (2013) Observational Probes of Cosmic Acceleration.
arXiv:1201.2434 - 5. Hoeneisen, B. (2000) A Simple Model of the Hierarchical Formation of Galaxies.
arXiv:astro-ph/0009071 - 6. Seo, H.-J., et al. (2010) High-Precision Predictions for the Acoustic Scale in the Nonlinear Regime. The Astrophysical Journal, 720, 1650.
https://doi.org/10.1088/0004-637X/720/2/1650 - 7. Albareti, F.D., et al. (2016) SDSS Collaboration. arXiv:1608.02013
- 8. Hoeneisen, B. (2016) Study of Baryon Acoustic Oscillations with SDSS DR12 Data and Measurement of ΩDE(a). arXiv:1607.02424
- 9. Planck Collaboration (2015) Results XIII, Astron. & Astrophys. Submitted.
arXiv:1502.01589v2 - 10. Font-Ribera, A., et al. (2014) Quasar-Lyman α Forest Cross-Correlation from BOSS DR11: Baryon Acoustic Oscillations. arXiv:1311.1767
- 11. Delubac, T., et al. (2014) Baryon Acoustic Oscillations in the Lyα Forest of BOSS DR11 Quasars. arXiv:1404.1801v2
- 12. Hoeneisen, B. (2016) Study of Baryon Acoustic Oscillations with SDSS DR12 Data and Measurements of Ωk and ΩDE(a). Part II. arXiv:1608.08486
- 13. Alam, S., et al. (2015) The Eleventh and Twelfth Data Releases of the Sloan Digital Sky Survey: Final Data from SDSS-III. Astrophysical Journal Supplement Series, 219, 12. arXiv:1501.00963
https://doi.org/10.1088/0067-0049/219/1/12 - 14. Peacock, J.A. (1999) Cosmological Physics. Cambridge University Press, Cambridge.
- 15. Dawson, K.S., Schlegel, D.J., Ahn, C.P., et al. (2013) The Baryon Oscillation Spectroscopic Survey of SDSS-III. Astronomical Journal, 145, 10.
https://doi.org/10.1088/0004-6256/145/1/10 - 16. Dawson, K.S., Kneib, J.-P., Percival, W.J., et al. (2016) The SDSS-IV Extended Baryon Oscillation Spectroscopic Survey: Overview and Early Data. Astronomical Jour-nal, 151, 44.
https://doi.org/10.3847/0004-6256/151/2/44 - 17. Chevallier, M. and Polarski, D. (2001) Accelerating Universes with Scaling Dark Matter. International Journal of Modern Physics D, 10, 213-223.
https://doi.org/10.1142/S0218271801000822 - 18. Linder, E.V. (2003) Exploring the Expansion History of the Universe. Physical Review Letters, 90, Article ID: 091301.
https://doi.org/10.1103/PhysRevLett.90.091301 - 19. Humphreys, E.M.L., Reid, M.J., Moran, J.M., Greenhill, L.J. and Argon, A.L. (2013) Toward a New Geometric Distance to the Active Galaxy NGC 4258. III. Final Results and the Hubble Constant. Astrophysical Journal, 775, 13.
https://doi.org/10.1088/0004-637X/775/1/13 - 20. Alam, S., et al. (2016) The Clustering of Galaxies in the Completed SDSS-III Baryon Oscillation Spectroscopic Survey: Cosmological Analysis of the DR12 Galaxy Sample. arXiv:1607.03155












