International Journal of Astronomy and Astrophysics
Vol.06 No.04(2016), Article ID:71858,6 pages
10.4236/ijaa.2016.64030
A Brief Review of the Amati Relation for GRBs
Walid J. Azzam
Department of Physics, College of Science, University of Bahrain, Sakhir, Kingdom of Bahrain

Copyright © 2016 by author and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY 4.0).
http://creativecommons.org/licenses/by/4.0/



Received: September 12, 2016; Accepted: November 6, 2016; Published: November 9, 2016
ABSTRACT
Gamma-ray bursts (GRBs) are the most powerful explosions in the universe. Although the exact mechanism behind these explosions remains elusive, GRBs hold great promise as cosmological probes for two main reasons: they have been observed up to very high redshift (z > 9), and their gamma-ray emission is unencumbered by any intervening dust. Several GRB energy and luminosity indicators have been discovered. These indicators correlate an observable quantity, like the intrinsic peak energy, Ep,i, in the nFn spectrum of a burst to an unobservable parameter like the equivalent isotropic energy, Eiso, or the isotropic peak luminosity, Lp,iso. This paper provides a brief review of one of these energy and luminosity indicators, the Amati relation, and discusses its potential use as a cosmological probe.
Keywords:
Gamma-Ray Bursts, Energy Correlations, Cosmological Probes

1. Introduction
There are currently several energy and luminosity correlations for gamma-ray bursts (GRBs). Some, like the lag-luminosity and variability relations [1] [2] , were obtained from the light curves, while others were obtained from the spectra and include the Amati relation [3] [4] [5] [6] , the Ghirlanda relation [7] , the Yonetoku relation [8] [9] , and the Liang-Zhang relation [10] . The importance of these correlations resides in their potential use as cosmological probes that might help in constraining cosmological models [10] - [16] , and also as tools that might help in probing the physics of GRBs [17] [18] .
Some studies have looked at possible inherent problems that these relations might suffer from, like the circularity problem and selection effects [19] [20] [21] [22] [23] . Other studies have investigated the possible redshift evolution of these correlations [24] - [29] since these relations are typically calibrated over a wide range in redshift (roughly 0.1 < z < 9), and thus it becomes incumbent to study their possible dependence on z, if they are to be utilized as cosmological probes.
The purpose of this paper is to provide a brief review of a well-known GRB energy and luminosity correlation―namely, the Amati relation, and to discuss its potential use as a cosmological probe.
2. The Amati Relation
The Amati relation is a correlation between a GRB’s equivalent isotropic energy, 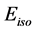 , and its intrinsic (i.e., rest-frame) peak energy,
, and its intrinsic (i.e., rest-frame) peak energy, 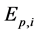 , in the nFn spectrum. It was first discovered by Amati et al. in 2002 and confirmed by later studies [3] [4] [5] [6] . It is necessary to know the redshift, z, of the GRB since
, in the nFn spectrum. It was first discovered by Amati et al. in 2002 and confirmed by later studies [3] [4] [5] [6] . It is necessary to know the redshift, z, of the GRB since  is calculated from the observed peak energy,
is calculated from the observed peak energy,  , by the following relation:
, by the following relation:
 (1)
(1)
The Amati relation is given by:
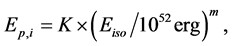 (2)
(2)
where K and m are constants, and  is in keV. In Amati’s original study, m » 0.5 and K » 95. However, later studies [30] with expanded data samples found mean values of
is in keV. In Amati’s original study, m » 0.5 and K » 95. However, later studies [30] with expanded data samples found mean values of  = 0.45 and
= 0.45 and  = 141.
= 141.
Alternatively, the Amati relation can be expressed logarithmically as:
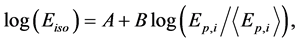 (3)
(3)
where the normalization, A, and the slope, B, are constants, and where  is the mean value of the intrinsic peak energy for the entire data sample. A recent study [31] involving 65 GRBs found that although the values of A and B fluctuate slightly depending on the redshift range of the sample, the approximate mean values are
is the mean value of the intrinsic peak energy for the entire data sample. A recent study [31] involving 65 GRBs found that although the values of A and B fluctuate slightly depending on the redshift range of the sample, the approximate mean values are  » 53 and
» 53 and 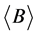 » 1, assuming
» 1, assuming 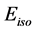 is measured in units of erg.
is measured in units of erg.
3. Robustness and Cosmological Prospects
Before we can utilize the Amati relation as a cosmological probe, we need to check its robustness. One of the central issues concerning the Amati relation is whether the fitting parameters are constant. A recent study [32] used a data sample of 47 GRBs to investigate the robustness of the Amati relation and to investigate whether the fitting parameters evolve with redshift. The authors found no redshift evolution of the Amati relation. Furthermore, although they found some outliers, they concluded that the Amati relation is genuine and not due to selection effects. This conclusion was confirmed by [31] who used a sample of 65 GRBs taken from [33] to investigate any possible redshift evolution. The authors binned the data after carrying out the proper z-correction and k-correction. They obtained good fits for the binned data and confirmed that the fitting parameters do not evolve with redshift.
Another problem that arises when we try to employ the Amati relation as a cosmological probe is the circularity problem, which refers to the fact that in order to calibrate the relation, one must assume a cosmological model in the first place. Two recent studies [34] [35] looked deeply into this problem and showed that it is essential to take proper account of this issue, otherwise an error of up to 13% could be introduced into the values of the cosmological parameters.
Early attempts to constrain cosmological parameters, like the matter density parameter WM, had limited success due to the paucity of data points [36] . Recently, however, there has been a revived interest in GRB cosmology mainly due to the increased availability of high caliber data. For instance, a recent study explored the cosmological evolution of 200 Swift GRBs and used the results to put limits on the star formation rate [37] . Other recent studies [38] [39] [40] have investigated how GRBs can be utilized to constrain dark energy, the first stars, and the pre-galactic metal enrichment. The Amati relation and other similar correlations have also taken a recent boost as cosmological probes, since the abundance of high quality data has reduced the extrinsic scatter in these correlations [36] .
4. Discussion and Summary
Gamma-ray bursts hold great promise as cosmological probes since they can be observed to huge distances (z > 9) and their radiation is unencumbered by any intervening dust. The most effective way of using them as cosmological probes is by utilizing one of the currently available energy and luminosity correlations.
In this brief review we focused on one of these correlations―namely, the Amati relation. It is a correlation between the equivalent isotropic energy and the intrinsic peak energy. Early attempts to employ the Amati relation as a cosmological probe faced several hurdles, like the circularity problem, the extrinsic scatter, and the paucity of data points. However, as high quality data samples have become available, the scatter in the correlation has diminished and the Amati relation has become more robust. In the near future, the Amati relation will be an effective cosmological tool that will shed light on many cosmological issues, like the density parameters and the star formation rate.
Acknowledgements
The author would like to thank the anonymous referee for the useful remarks that helped improve the paper.
Cite this paper
Azzam, W.J. (2016) A Brief Review of the Amati Relation for GRBs. International Journal of Astronomy and Astrophysics, 6, 378-383. http://dx.doi.org/10.4236/ijaa.2016.64030
References
- 1. Norris, J.P. et al. (2000) Connection between Energy Dependent Lags and Peak Luminosity in Gamma-Ray Bursts,. The Astrophysical Journal, 534, 248-257.
http://dx.doi.org/10.1086/308725 - 2. Fenimore, E.E. and Ramirez-Ruiz, E. (2000) Redshifts for 220 BATSE Gamma-Ray Bursts Determined by Variability and the Cosmological Consequences. astro-ph/0004176
- 3. Amati, L., et al. (2002) Intrinsic Spectra and Energetics of BeppoSAX Gamma-Ray Bursts with Known Redshifts. Astronomy and Astrophysics, 390, 81-89.
http://dx.doi.org/10.1051/0004-6361:20020722 - 4. Amati, L. (2006) The Ep,i–Eiso Correlation in Gamma-Ray Bursts: Updated Observational Status, Re-Analysis and Main Implications,. Monthly Notices of the Royal Astronomical Society, 372, 233-245.
http://dx.doi.org/10.1111/j.1365-2966.2006.10840.x - 5. Amati, L., et al. (2008) Measuring the Cosmological Parameters with the Ep,i–Eiso Correlation of Gamma-Ray Bursts. Monthly Notices of the Royal Astronomical Society, 391, 577-584.
http://dx.doi.org/10.1111/j.1365-2966.2008.13943.x - 6. Amati, L., et al. (2009) Extremely Energetic Fermi Gamma-Ray Bursts Obey Spectral Energy Correlations. Astronomy and Astrophysics, 508, 173-180.
http://dx.doi.org/10.1051/0004-6361/200912788 - 7. Ghirlanda, G., et al. (2004) The Collimation-Corrected Gamma-Ray Burst Energies Correlate with the Peak Energy of TheirvFv Spectrum. The Astrophysical Journal, 616, 331-338.
http://dx.doi.org/10.1086/424913 - 8. Yonetoku, D., et al. (2004) Gamma-Ray Burst Formation Rate Inferred from the Spectral Peak Energy-Peak Luminosity Relation. The Astrophysical Journal, 609, 935-951.
http://dx.doi.org/10.1086/421285 - 9. Ghirlanda, G., et al. (2010) Spectral-Luminosity Relation within Individual Fermi Gamma-Ray Bursts. Astronomy and Astrophysics, 511, A43-A53.
http://dx.doi.org/10.1051/0004-6361/200913134 - 10. Liang, E. and Zhang, B. (2005) Model-Independent Multivariable Gamma-Ray Burst Luminosity Indicator and Its Possible Cosmological Implications. The Astrophysical Journal, 633, L611-L623.
http://dx.doi.org/10.1086/491594 - 11. Ghirlanda, G., et al. (2006) Cosmological Constraints with GRBs: Homogeneous vs. Wind Density Profile,. Astronomy and Astrophysics, 452, 839-844.
http://dx.doi.org/10.1051/0004-6361:20054544 - 12. Capozziello, S. and Izzo, L. (2008) Cosmography by Gamma-Ray Bursts. Astronomy and Astrophysics, 490, 31-36.
http://dx.doi.org/10.1051/0004-6361:200810337 - 13. Demianski, M. and Piedipalumbo, E. (2011) Standardizing the GRBs with the Amati Ep,i–Eiso Relation: The Updated Hubble Diagram and Implications for Cosmography. Monthly Notices of the Royal Astronomical Society, 415, 3580-3590.
http://dx.doi.org/10.1111/j.1365-2966.2011.18975.x - 14. Azzam, W.J. and Alothman, M.J. (2006) Constraining Cosmological Parameters through Gamma-Ray Bursts. Advances in Space Research, 38, 1303-1306.
http://dx.doi.org/10.1016/j.asr.2004.12.019 - 15. Azzam, W.J. and Alothman, M.J. (2006) Gamma-Ray Burst Spectral-Energy Correlations as Cosmological Probes. Il Nuovo Cimento B, 121, 1431-1432.
- 16. Dai, Z.G., Liang, E.W. and Xu, D. (2004) Constraining ΩM and Dark Energy with Gamma-Ray Bursts,. The Astrophysical Journal, 612, L101-L104.
http://dx.doi.org/10.1086/424694 - 17. Zhang, B. and Mészáros, P. (2002) An Analysis of Gamma-Ray Burst Spectral Break Models. The Astrophysical Journal, 581, 1236-1247.
http://dx.doi.org/10.1086/344338 - 18. Thompson, C., Mészáros, P. and Rees, M.J. (2007) Thermalization in Relativistic Outflows and the Correlation between Spectral Hardness and Apparent Luminosity in Gamma-Ray Bursts. The Astrophysical Journal, 666, 1012-1023.
http://dx.doi.org/10.1086/518551 - 19. Li, H., et al. (2008) Overcoming the Circular Problem for Gamma-Ray Bursts in Cosmological Global-Fitting Analysis. The Astrophysical Journal, 680, 92-99.
http://dx.doi.org/10.1086/529582 - 20. Butler, N.R., et al. (2009) Generalized Tests for Selection Effects in Gamma-Ray Burst High-Energy Correlations. The Astrophysical Journal, 694, 76-83.
http://dx.doi.org/10.1088/0004-637X/694/1/76 - 21. Ghirlanda, G., Nava, L., Ghisellini, G., Firmani, C. and Cabrera, J.I. (2008) The Epeak-Eiso Plane of Long Gamma-Ray Bursts and Selection Effects. Monthly Notices of the Royal Astronomical Society, 387, 319-330.
http://dx.doi.org/10.1111/j.1365-2966.2008.13232.x - 22. Nava, L., Ghirlanda, G. and Ghisellini, G. (2009) Selection Effects on GRB Spectral-Energy Correlations. arXiv:0902.1522
- 23. Graziani, C. (2011) GRBs as Standard Candles: There Is No “Circularity Problem” (and There Never Was). New Astronomy, 16, 57-64.
http://dx.doi.org/10.1016/j.newast.2010.08.001 - 24. Li, L.-X. (2007) Variation of the Amati Relation with Cosmological Redshift: A Selection or an Evolution Effect? Monthly Notices of the Royal Astronomical Society, 379, L55-L59.
http://dx.doi.org/10.1111/j.1745-3933.2007.00333.x - 25. Tsutsui, R., Nakamura, T., Yonetoku, D., Murakami, T., Tanabe, S. and Kodama, Y. (2008) Redshift-Dependent Lag-Luminosity Relation in 565 BATSE Gamma-Ray Bursts. Monthly Notices of the Royal Astronomical Society, 386, L33-L37.
http://dx.doi.org/10.1111/j.1745-3933.2008.00455.x - 26. Azzam, W.J., Alothman, M.J. and Guessoum, N. (2009) A Possible Redshift Evolution of the Time-Lag and Variability Luminosity Relations for Long Gamma-Ray Bursts. Advances in Space Research, 44, 1354-1358.
http://dx.doi.org/10.1016/j.asr.2009.08.003 - 27. Azzam, W.J. and Eid, H.A. (2011) Variation of the Lag-Luminosity Relation with Redshift for Swift GRBs. The European Physical Journal Plus, 126, 74-78.
http://dx.doi.org/10.1140/epjp/i2011-11074-0 - 28. Azzam, W.J. and Eid, H.A. (2011) Redshift Evolution of the Lag Relation for Swift GRBs. AIP Conference Proceedings, 1358, 227-230.
http://dx.doi.org/10.1063/1.3621777 - 29. Azzam, W.J. (2012) Dependence of the GRB Lag-Luminosity Relation on Redshift in the Source Frame. International Journal of Astronomy and Astrophysics, 2, 1-5.
http://dx.doi.org/10.4236/ijaa.2012.21001 - 30. Zitouni, H., Guessoum, N. and Azzam, W.J. (2014) Revisiting the Amati and Yonetoku Relations with Swift GRBs. Astrophysics and Space Science, 351, 267-279.
http://dx.doi.org/10.1007/s10509-014-1839-5 - 31. Azzam, W.J. and Alothman, M.J. (2013) Redshift Independence of the Amati and Yonetoku Relations for Gamma-Ray Bursts. International Journal of Astronomy and Astrophysics, 3, 372-375.
http://dx.doi.org/10.4236/ijaa.2013.34042 - 32. Nava, L., et al. (2012) A Complete Sample of Bright Swift Long Gamma-Ray Bursts: Testing the Spectral-Energy Correlations. Monthly Notices of the Royal Astronomical Society, 421, 1256-1264.
http://dx.doi.org/10.1111/j.1365-2966.2011.20394.x - 33. Geng, J.J. and Huang, Y.F. (2013) On the Correlations of Low-Energy Spectral Indices and Redshifts of Gamma-Ray Bursts. The Astrophysical Journal, 764, 75-83.
http://dx.doi.org/10.1088/0004-637X/764/1/75 - 34. Amati, L. and Della Valle, M. (2013) Measuring Cosmological Parameters with Gamma-Ray Bursts. International Journal of Modern Physics D, 22, Article ID: 1330028.
- 35. Dainotti, M.G., Cardone, V.F., Piedipalumbo, E. and Capozziello, S. (2013) Slope Evolution of GRB Correlations and Cosmology. Monthly Notices of the Royal Astronomical Society, 436, 82-88.
http://dx.doi.org/10.1093/mnras/stt1516 - 36. Azzam, W.J. and Al Dallal, S. (2015) Gamma-Ray Bursts: Origin, Types, and Prospects. Journal of Magnetohydrodynamics and Plasma Research, 20, 367.
- 37. Petrosian, V., Kitanidis, E. and Kocevski, D. (2015) Cosmological Evolution of Long Gamma-Ray Bursts and the Star Formation Rate. The Astrophysical Journal, 806, 44-52.
http://dx.doi.org/10.1088/0004-637X/806/1/44 - 38. Wang, F.Y., Dai, Z.G. and Liang, E.W. (2015) Gamma-Ray Burst Cosmology. New Astronomy Review, 67, 1-17.
http://dx.doi.org/10.1016/j.newar.2015.03.001 - 39. Wang, J.S., Wang, F.Y., Cheng, K.S. and Dai, Z.G. (2016) Measuring Dark Energy with the Eiso-Ep Correlation of Gamma-Ray Bursts Using Model-Independent Methods. Astronomy and Astrophysics, 585, Article No. A68.
http://dx.doi.org/10.1051/0004-6361/201526485 - 40. Dainotti, M.G., Petrosian, V., Willingale, R., O’Brien, P., Ostrowski, M. and Nagataki, S. (2015) Luminosity-Time and Luminosity-Luminosity Correlations for GRB Prompt and Afterglow Plateau Emissions. Monthly Notices of the Royal Astronomical Society, 451, 3898-3908.
http://dx.doi.org/10.1093/mnras/stv1229

