International Journal of Astronomy and Astrophysics
Vol.07 No.02(2017), Article ID:76038,7 pages
10.4236/ijaa.2017.72006
A Wave Function for the Spin of the Early Universe Derived from the Wheeler-DeWitt Equation
Juan Carlos Echaurren
Bilbao 796, Calama, Chile

Copyright © 2017 by author and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY 4.0).
http://creativecommons.org/licenses/by/4.0/



Received: May 11, 2016; Accepted: May 2, 2017; Published: May 5, 2017
ABSTRACT
The wave function for the spin the early universe is obtained through the adaption of the quantum formalism to one solution of the Wheeler-DeWitt’s equation [1] , associated with the wave function of the universe. In addition, some observations performed by Stephen Hawking in relation to the vorticity of the universe [2] are used. This wave function for the spin could be used for indirectly to demonstrate the presence of dark matter in the universe.
Keywords:
Spin, Vorticity, Rotation, Angular Moment, Wave Function of the Universe, Blueshift, Great Attractor

1. Introduction
1.1. General Aspects
Instants after the Big Bang a incandescent infinitesimal amount of energy, with high degrees of indistinguishability, is projected externally in the form of a closed space, this projection transfers a combined rotation, to the early universe, consisting of both, of an orbital rotation around a virtual center, and of an intrinsic rotation of the universe on its own axis (spin).
The initial magnitudes of these rotations are enormous, but will decrease gradually during the inflationary stage “10−32 s”, and for the rest of the expansion but will not disappear.
During the inflationary stage these rotations will remain independent, but on cooling of the matter in the universe during the expansion, and its corresponding increase of volume, will cause, that the intrinsic rotation (spin) and the orbital rotation in the early universe lose velocity. Then the superimposing of both rotations, will affect the movement of the galaxies near the outer edge of the universe.
This phenomenon of spin can be determined indirectly through astronomical observations of the blueshift of galaxies beyond the great attractor, near of the outer border of the universe galaxies, this could be the physical cause of the hypothetical dark flow, proposed to explain some surprising results associated with the movement of large galaxy clusters.
1.2. Specific Aspects
The universe and everything contained in it (stars, galaxies, clusters, etc.) is in constant motion from the Big Bang until the present. All this current movement is inherited from the energy released in the Big Bang. This transfer of motion would take place in two stages:
i. From the geometry we know that in a sphere, its surface area (AS), 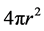 ,
,
and its volume,  , are equal when the radius r of the sphere is numeri-
, are equal when the radius r of the sphere is numeri-
cally equal to 3. When this radio changes, by above or below of 3, the following scenario would be generated:
i.1. When r > 3 Þ AS < Vsphere. In this case the surface-area-to-volume ratio tends to decrease as the universe expands, causing that the movement of spin, can to replace the orbital generated in the Big Bang.
i.2. When r < 3 Þ AS > Vsphere, therefore in the moments before the Big Bang, the surface-area-to- volume ratio, would be high enough, as for to generate a great force on the virtual surface area of the unborn universe. This force is the origin of the initial orbital movement.
i.3. The law of large numbers, can be applied here as well: If we take all the possible events leading up to the Big Bang, and all the possible paths of the tiny universe after the Big Bang, including those universes orbiting around a virtual center Un, we would see a convergence to our current universe, UPRESENT. If we increase all these possible events to infinity, the probability of this convergence is 100% (strong law), this can be written as:
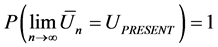 (1)
(1)
Since distant stars have been observed, with a blue shift in its light, i.e., approaching, it is possible to infer a small current rotation movement. Then in the beginning of time, this rotation would have reached enormous magnitude, giving the tiny universe an additional orbital motion.
A scheme of this phenomenon is shown as follows (Figure 1):
The mathematical formulation shown here is on the total angular moment ĴU, associated to the early universe, according to one polynomial solution Y(G,r) derived on Wheeler-DeWitt’s equation. The total angular moment ĴU, is expressed depending on both, the angular orbital moment ÛU and of the angular intrinsic moment of the universe, ŜU. For the mathematical development we work with a wave function y(r,t), which is deduced from Y(G, r) in where the
Figure 1. Generation process, for both spin and rotation orbital, of the early universe. (a) Inflationary period; (b) Expansion of the early universe, after of the inflationary period.
variables r y t, are expressed as real functions of the shape,
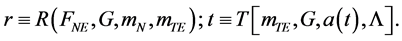 (2)
(2)
where FNE is a gravitational function between the nucleus of the universe and its external edge, G is the Newton-Cavendish constant of Universal Gravitation, mN is the nucleus mass, mTE is the total mass of the border, a(t) the scale factor, L º 8pGrvac is the cosmological constant, and rvac is the vacuum energy density.
2. Model and Results
2.1. Solution to the Wheeler-DeWitt’s Equation
The treatment and solution of this equation is realized in its classic form, which is expressed in function of the scale factor a(t), associated with the space-time expansion, and the corresponding growth of the universe. The solution is obtained according to the Laplace methodology. The obtaining of one differential expression for the Wheeler-DeWitt’s equation, is achieved through the Einstein’s equation for a FRW cosmology,
 (3)
(3)
where, L º 8pGrvac is the cosmological constant, and rvac is the vacuum energy density. An equivalent expression for this equation in a closed FRW universe, is of the form,
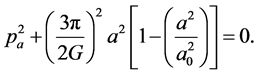 (4)
(4)
where pa is the canonical momentum. Finally the quantization of this expression allows us to obtain the Wheeler-DeWitt equation defined by,
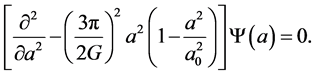 (5)
(5)
Then, applying Laplace transforms [3] to Equation (5),
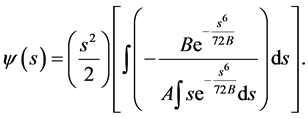 (6)
(6)
where, 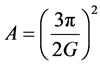 and
and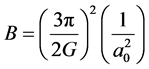 . The term in square brackets is reduced to the expression,
. The term in square brackets is reduced to the expression,
 (7)
(7)
where, . Applying a transformation to Taylor polynomial of fourth order in this expression, we have,
. Applying a transformation to Taylor polynomial of fourth order in this expression, we have,
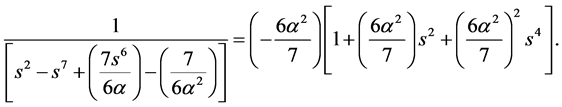 (8)
(8)
Replacing this result in the Equation (7), allows to obtain a partial result for the universe wave function, as follows,
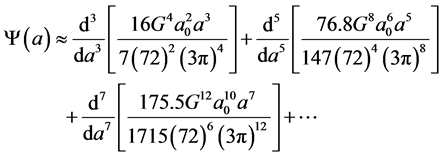 (9)
(9)
where the previous expression is valid for any type of function associated to the scale factor a(t) [4] [5] [6] . Finally we can generalize this wave function, as follows,
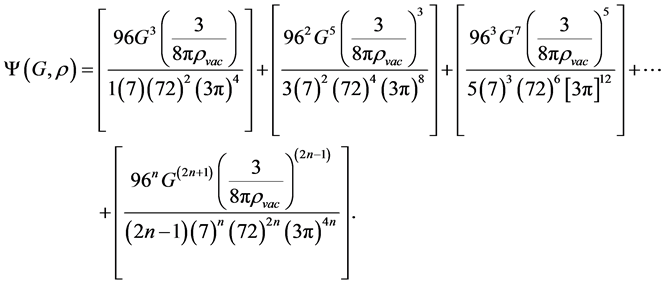 (10)
(10)
or,
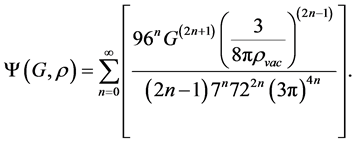 (11)
(11)
where, n Î N È {0}, G is the Newton?Cavendish constant of Universal Gravitation, and rvac is the vacuum energy density. Then, according to a fast examination of this polynomial representation for the evolution of the universe, we see that for rvac ® 0, the function Y is strongly increasing, generating an almost indefinite expansion, of the same form when rvac ® ¥, Y ® 0, generating conditions for a collapsed universe. The Equation (11) is an exact and infinite representation of the universe, where every term is associated with a particular condition in its evolution, being the Laplace transforms fundamental for the obtaining of this solution.
2.2. Getting a Wave Function for the Spin of the Universe
Defining the parameter l [7] , as the polynomial components associated to the Equation (11), is possible to obtain,
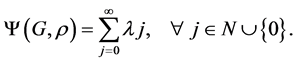 (12)
(12)
The application of a rotation C(a) [6] , to this early universe, allows to obtain,

Being Dljlj' the components of a square matrix D. Then expressing to y(r,lj) as the components of a vertical matrix yV(r) we obtain,

Continuing with the development we obtain,

Being ÛU the operator angular orbital moment of the universe defined as,

And being besides, 

Finally,

Then being,

The conditions for a young universe are obtained when n ® 0 and j ® 0, then,

Resolving for

3. Discussion
The negative sign that shown in Equation (21) represents one imaginary component of 
spin function shows that when rvac ® ¥, 

increasing. Researches realized by Stephen Hawking show that the universe, according to observations of the microwave background radiation, could possess to large scale, homogeneous vorticity, between 10−14 and 7 × 10−17 rad yr−1 if the universe is spatially closed, i.e., between 5.71 × 10−13 and 4.00 × 10−15 degrees yr−1 respectively. Then, if the rotation of the universe has been very slow from the BigBang to its current expansion, the norm of the spin function, 


Cite this paper
Echaurren, J.C. (2017) A Wave Function for the Spin of the Early Universe Derived from the Wheeler-DeWitt Equation. International Journal of Astronomy and Astrophysics, 7, 62-68. https://doi.org/10.4236/ijaa.2017.72006
References
- 1. Athatz, D. (1994) Quantum Cosmology for Pedestrians. American Journal of Physics, 62.
- 2. Hawking, S. (1969) On the Rotation of the Universe. Mon. Monthly Notices of the Royal Astronomical Society, 142, 129-141.
- 3. Spiegel, M.R. (1990) Laplace Transforms. McGraw-Hill/Interamericana de México, S.A. de C.V., 65-66.
- 4. Gott III, J.R. and Li, L.-X. (1998) Can the Universe Create Itself? Physical Review D, 58, 023501-1, 023501-43.
- 5. Lü, H., Maharana, J., Mukherji, S. and Pope, C.N. (1998) Cosmological Solutions, P-Branes, and the Wheeler-DeWitt Equation. Physical Review D, 57, 2219-2229.
https://doi.org/10.1103/PhysRevD.57.2219 - 6. Overduin, J. and Cooperstock, F.J. (1998) Evolution of the Scale Factor with a Variable Cosmological Term. Physical Review D, 58, 43506-1, 43506-23.
- 7. Yndurain, F. (1988) Quantum Mechanic. Alianza Editorial, S.A., Madrid, 23-36.


