Received 17 February 2015; accepted 7 March 2015; published 10 March 2015

ABSTRACT

A sufficiently large star will collapse to form a Black Hole Singularity due to Gravitational Pressure beyond Neutron Degeneracy. A Black Hole exhibits extremely strong Gravitational attraction that no particle or electromagnetic radiation can escape from it. The boundary of the region from which no escape is possible is called Event Horizon. In this work it is proposed that there exists a Neutron star smaller than Event Horizon, which is termed as Black Neutron Star. Furthermore an alternative method is proposed to ascertain the maximum permissible mass limit of the Neutron Star and the minimum mass limit of the naturally occurring gravitationally collapsed Black hole.

Keywords:

Neutron Star, Black Hole, Gravitational

1. Introduction

The primary source of energy of a Main Sequence Star is nuclear fusion at its central core, this nuclear fusion releases energy which exerts an outward radiation pressure countering the gravitational collapse and maintaining the hydrostatic equilibrium. The onset of fusion process in significant mass star is always with Hydrogen fusion, first to deuterium and then to Helium. Eventually the supply of Hydrogen gets exhausted and the Gravitational Pressure forces the core to get contracted.

Depending on the core mass this Gravitational contraction is countered either by Electron degeneracy or by further initiation of fusion of Helium present in the core. In 1935, Chandrasekhar [1] proposed an upper limit of formation of white dwarf through Electron Degeneracy which is known as Chandrasekhar Limit (1.44 Solar Mass).

If the mass of the core is more than the Chandrasekhar Limit, then Gravitational Collapse causes sufficient increase in temperature to enable Helium fusion to higher atoms to finally Fe⁵⁶. Once the iron is formed in the fusion process, no longer sustainable fusion process can take place as beyond this, the fusion process is endothermic.

Once this stage is achieved, the star starts collapsing as now no longer counter balancing fusion energy is produced. Since the core mass is higher than the Chandrasekhar Limit and hence even the Electron degeneracy can no longer provide sufficient counter balancing pressure to hold on to Gravitational Collapse. These electrons get captured by protons and in the process Neutrons are left in abundance, the continued inward pressure forces Neutrons to go to their lowest Energy States and developed Neutron Degeneracy Pressure counters the Gravitational Pressure and a Hydrostatic Equilibrium is established thus forming a Neutron Star [2] [3] .

In 1939, J R Oppenheimer and G Volkoff using the work of R C Tolman proposed the limiting mass of the Neutron Star at 0.7 Solar Mass, this is called as TOV limit [4] . This limit is quite low, in fact lower than the Chandrasekhar Limit for Electron Degeneracy which is not realistic and hence modern estimates put this limit to 1.4 to 3.0 Solar Masses.

The Neutron Degeneracy Pressure calculations define the relationship between mass of the Neutron Star core and its radius as:

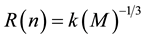
If the mass of the core of the collapsing star is more than the TOV limit then even the Neutron Degeneracy cannot provide sufficient counter balancing pressure against Gravitational Collapse and a Black hole is formed. A Black Hole exhibits extremely strong Gravitational attraction that no particle or electromagnetic radiation can escape from it. The boundary of the region from which no escape is possible is called Event Horizon. This is mathematically defined as Schwarzschild radius; therefore if an object of mass M is smaller than the size of Schwarzschild radius then it is termed as Black Hole.

For an object of mass M the Schwarzschild radius R(s) is

In this work the formation of Neutron Star is understood from a perspective of the Spherical Packing aspect, and it is observed that there are three distinct core mass ranges, one from 1.4 - 2.7 Solar Mass, second from 2.7 to 3.24 Solar Mass and third from 3.24 solar Mass and higher. The first range can form a Visible Neutron Star, the second range star is also a visible star but it will have to have certain exotic matter beyond Neutrons and third range will form a Neutron Star of the radius smaller than Schwarzschild radius. This star can be termed as Black neutron Star as no light can escape out of it.

1.1. Revised Pauli’s Exclusion Principle and Neutron Degeneracy

As referred above once the Hydrostatic equilibrium is disturbed due to exhaustion of Hydrogen required for fusion, the star collapses towards Neutron Degeneracy if the mass of the core of the star is higher than Chandrasekhar Limit. J R Oppenheimer and G Volkoff carried out certain computations by assuming this compressed Neutron matter as Cold Fermi Gas and arrived at TOV Limit.

In this work an alternative method is proposed to arrive at Neutron Star Mass limit based on Spherical Packing aspect. It is proposed that this Gravitational Pressure will create extra ordinary situation in which Neutrons are pressed like any other spherical object. The fermions cannot stick to Pauli’s Exclusion Principle under such extreme pressure. This is no violation of Pauli’s Exclusion Principle; it is just that the same gets redefined a bit which paves way for bosonic compactness as…,

“Two identical fermions (particles with half-integer spin) cannot occupy the same quantum state simultaneously, but they can be forced to occupy the same quantum state under extreme external pressure as the Δx is made to approach zero, where Δx is the uncertainty in position”.

1.2. Spherical Packing of Neutrons

Under such extreme gravitational pressure, it is most likely that the Neutrons will pack themselves completely densely in the given core space. This dense packing can be understood from the Kepler Conjecture [5] [6] . So if there are n Neutrons each of radius r, then these Neutrons will just fit inside a spherical space of radius R(p) where we call this as packing radius.

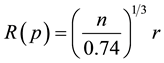
2. Discussions and Black Neutron Star

A comparative analysis of various radii is carried out to establish that even inside the Event Horizon a neutron Star may exist which is termed as Black Neutron Star.

Table 1 represents the typical values of these radii in Kms for various solar masses, for computation purpose it is taken that one Solar Mass has 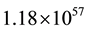Neutrons and the realistic core radius of neutron is 0.55 fm, the value of radius of Neutron has substantial impact on tabulated values.

It is shown that the Schwarzschild radius up to 3.24 solar mass is less than the packing radius for the available neutrons. This is a very crucial result simply because for any object smaller than 3.24 solar mass, the collapse to Event Horizon is not possible without actually pushing the neutrons beyond their extreme possible packing arrangement thus defining the lower limit on the mass of Invisible Star (Black hole) as 3.24 Solar Mass.

Similarly if the star is more than 3.24 solar mass, then there is still room for neutron compactness beyond Event Horizon as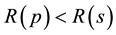. The conclusion is that we can have a Black Neutron star. With this conclusion author proposes that a physical Neutron Star exists which is smaller than Event Horizon in size.

Another interesting observation is that the packing radius up to 2.65 solar mass is less than the neutron star radius, signifying that a core of more than 2.65 solar mass will have to press the neutrons beyond their best possible packing arrangement, if the neutron star can at all be formed for a core of more than 2.65 solar mass. The inescapable conclusion is that we cannot have a visible neutron star of more than 2.65 Solar Mass. This observation is categorized as per mass range as follows:

2.1. Mass of Star Core between 1.4 to 2.65 Solar Mass

As per Table 1 above for this range

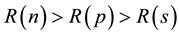
so technically from the pure dynamics point of view, there is ample space for Neutrons to move around even after neutron degeneracy pressure has countered the gravity, it cannot be stated that due to Heisenberg uncertainty principle they have become completely relativistic (speed at par with speed of light). So a stable visible neutron Star can be formed for such mass range without causing any ambiguity.

2.2. Mass of Star Core between 2.65 to 3.24 Solar Mass

A very critical mass which is neither conducive for neutron Star and nor for black Hole.

In this case the neutron star radius required to sustain the Gravitational Pressure becomes less than the Packing radius, that implies that something must happen to such densely packed neutrons like either neutrons get converted into quarks or convert into energy, but then it no longer can be stated that this is a Neutron Star, so a visible neutron star is possible only up to around 2.65 Solar Mass. This also explains and predicts that in general visible neutron Stars will be in existence between 1.4 to 2.65 Solar Mass and also of radius around 11 - 9 Kms.

This inflection point of 2.65 Solar Mass defines the upper limit of a visible Neutron Star Mass. The significance of this point is that above this mass the required Neutron Star radius is less than packing radius, thus the same is not possible with all Neutron in the core.

It is also useful to note that even for this mass the Schwarzschild radius is still lower than these two radii, thus effectively light can still escape and star will be visible.

2.3. Mass of Star Greater than 3.24 Solar Mass

This is the case where

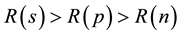
That means a visible Neutron star of 3.24 solar mass and above is completely ruled out, now it is the question if the same gets converted into Black Hole Singularity or adopts some other mechanism.

Since the star is large enough the additional Gravitational pressure will squeeze the Neutron core to an extent that it shrinks beyond the Event Horizon but still larger than packing radius. In fact depending on the star mass the internal neutron degeneracy pressure will sustain the gravitational pressure even beyond the Event Horizon since the position of Neutrons keeps getting extremely rigid and fixed with reducing positional uncertainty and Heisenberg uncertainty principle would require the Neutrons to become increasingly relativistic, this will ensure certain stability of star even if its radius is smaller than Event Horizon. So it is quite likely that we get stellar objects of larger mass than 3.24 solar mass but inside the Event Horizon, which are perfectly definable structures (without singularity) and they can be termed as Invisible Neutron Stars as their radii is less than Schwarzschild radius and more than packing radius.

3. Conclusion

It is proposed that an invisible Neutron Star may exist wherein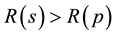, this will enable us to look for physical presence of a star beyond Event Horizon, which so far being treated as singularity thus out of bounds of physical understanding. An upper limit is also evaluated for the mass of the visible Neutron star and the lower mass limit for the naturally occurring gravitationally collapsed Black hole is also computed. These parameters are Neutron radius dependent.

References