International Journal of Astronomy and Astrophysics
Vol.4 No.3(2014), Article
ID:48777,8
pages
DOI:10.4236/ijaa.2014.43038
Bianchi Type-V Cosmological Model with Linear Equation of State in Brans-Dicke Theory of Gravitation
Sharad Kandalkar*, Seema Samdurkar
Department of Mathematics, Govt. Vidarbha Institute of Science & Humanities, Amravati (M.S.), India
Email: *spkandalkar2004@yahoo.com
Copyright © 2014 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 31 May 2014; revised 28 June 2014; accepted 25 July 2014
ABSTRACT
A Bianchi type-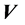 space time is considered with linear equation of state in the scalar tensor theory of gravitation proposed by Brans and Dicke. We use the assumption of constant deceleration parameter and power law relation between scalar field
space time is considered with linear equation of state in the scalar tensor theory of gravitation proposed by Brans and Dicke. We use the assumption of constant deceleration parameter and power law relation between scalar field 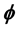 and scale factor
and scale factor 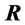 to find the solutions. Some physical and kinematical properties of the model are also discussed.
to find the solutions. Some physical and kinematical properties of the model are also discussed.
Keywords:Bianchi Type-V Model, Brans-Dicke Theory, Linear Equation of State

1. Introduction
Einstein’s [1] general theory of relativity has provided a sophisticated theory of gravitation which has been very successful in describing gravitational phenomenon and also served as a basis for models of the universe. The homogeneous isotropic expanding model based on general relativity appears to provide a grand approximation to the observed large-scale properties of the universe. However since Einstein first published his theory of gravitation there have been many criticisms of general relativity because of lack of certain “desirable” features in the theory. For example, Einstein himself pointed out that general relativity does not account satisfactorily for inertial properties of matter i.e. Mach’s principle is not substantiated by general relativity. So, in recent years, several theories of gravitation have been proposed as alternatives for Einstein’s theory. The most important among them are scalar-tensor theories of gravitation formulated by Jordan [2] , Brans and Dicks [3] , Nordtvedt [4] , Ross [5] and Schmidt et al. [6] .
Brans and Dicke [3] introduced a scalar-tensor theory of gravitation involving a scalar function in addition to the familiar general relativistic metric tensor. In this theory the scalar field has the dimensions of inverse of the gravitational constant and its role is confined to its effect on gravitational field equations. Several aspects of Brans-Dicke cosmology have been extensively investigated by many authors. The work of Singh and Rai [7] give a detailed survey of Brans-Dicke cosmological models discussed by several authors. Nariai [8] , Reddy and Rao [9] , Banerjee and Santos [10] , Singh et al. [11] , Ram [12] , Ram and Singh [13] , Berman et al. [14] , Reddy et al. [15] are some of the authors who have investigated several aspects of this theory. Reddy and Venkateswara Rao [16] and Reddy et al. [17] discussed Bianchi type I cosmological models with negative constant declaration parameter in scalar tensor theories formulated by Brans-Dicke theory and Saez-Ballester theory [18] .
There has been considerable interest in the study of spatially homogeneous, anisotropic cosmological models. Bianchi type 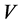 space-times, being a straight forward generalization of FRW universe with negative curvature are interesting to study because they contain isotropic special cases and allow arbitrarily small anisotropy levels at any instant of cosmic time. Fransworth [19] , Collins [20] , Maartens and Nel [21] , Wainwright et al. [22] have studied Bianchi type
space-times, being a straight forward generalization of FRW universe with negative curvature are interesting to study because they contain isotropic special cases and allow arbitrarily small anisotropy levels at any instant of cosmic time. Fransworth [19] , Collins [20] , Maartens and Nel [21] , Wainwright et al. [22] have studied Bianchi type 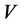 cosmological models. Nayak and Sahoo [23] have investigated Bianchi type
cosmological models. Nayak and Sahoo [23] have investigated Bianchi type 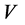 models for matter distribution admitting anisotropic pressure and heat flow. Several authors studied Bianchi type
models for matter distribution admitting anisotropic pressure and heat flow. Several authors studied Bianchi type 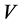 in different context [24] -[37] .
in different context [24] -[37] .
Motivated by above discussion, in this paper we have obtained exact solutions of the Einstein field equations of Bianchi type 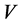 Cosmological model with linear equation of state in the scalar tensor theory of gravitation proposed by Brans and Dicke.
Cosmological model with linear equation of state in the scalar tensor theory of gravitation proposed by Brans and Dicke.
2. The Metric and Field Equations
We consider Bianchi type-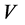 space time described by the line element
space time described by the line element
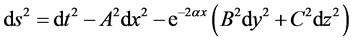 (1)
(1)
where ![]() and
and 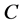 are function of cosmic time
are function of cosmic time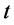 .
.
Brans-Dicke field equations for combined scalar and tensor field are
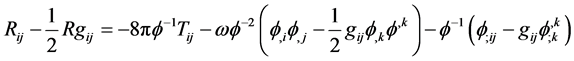 (2)
(2)
and
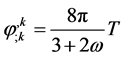 (3)
(3)
where 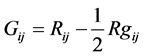 is an Einstein tensor,
is an Einstein tensor, 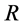 is the scalar curvature,
is the scalar curvature, ![]() is a dimension less constant and
is a dimension less constant and
![]() is the stress energy tensor of the matter, comma and semicolon denote partial and co-variant differentiation respectively.
is the stress energy tensor of the matter, comma and semicolon denote partial and co-variant differentiation respectively.
Also, we have energy-conservation equation
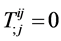 (4)
(4)
are consequences of the field Equations (2) and (3).
The energy momentum tensor
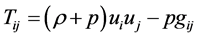 (5)
(5)
where 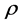 is the energy density of the perfect fluid and
is the energy density of the perfect fluid and ![]() is its pressure. Here the four velocity vector
is its pressure. Here the four velocity vector 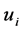 and
and 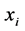 satisfy the standard relations
satisfy the standard relations
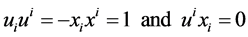 (6)
(6)
Here we use line are quation of state given by Thirukkanesh and Maharaj [38] for perfect fluid as
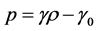 (7)
(7)
where 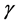 and
and 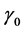 constants.
constants.
In the moving coordinate system, we have from (5) and (6)
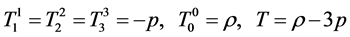 (8)
(8)
Now the Brans-Dicke field Equations (2) and (3) for the metric (1) with the help of (5) to (7) can be written as
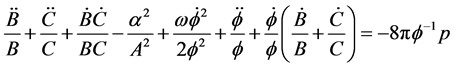 (9)
(9)
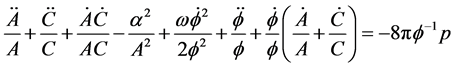 (10)
(10)
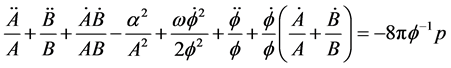 (11)
(11)
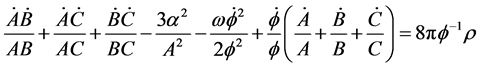 (12)
(12)
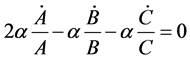 (13)
(13)
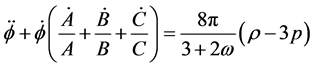 (14)
(14)
where dot over the field variables denote differentiation with respect to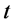 .
.
Spatial volume and the scale factor for the metric (1) are defined respectively, by
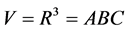 (15)
(15)
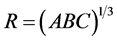 (16)
(16)
The physical quantities of observational interest in cosmology are the expansion scalar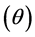 , shear scalar
, shear scalar 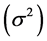 and the mean anisotropic parameter
and the mean anisotropic parameter 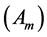 defined as
defined as
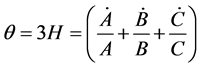 (17)
(17)
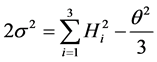 (18)
(18)
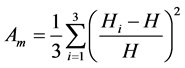 (19)
(19)
3. Solutions and the Model
From Equations (10) and (11), we get
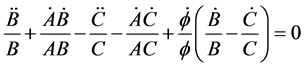 (20)
(20)
Integrating Equation (13), we obtain
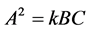 (21)
(21)
where ![]() is a constant of integration. The constant
is a constant of integration. The constant![]() , without loss of generality, can be chosen as unity so that we have, from Equation (21),
, without loss of generality, can be chosen as unity so that we have, from Equation (21),
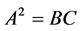 (22)
(22)
In order to get a deterministic solution, we take the following plausible physical condition:
i) The shear scalar ![]() is proportional to scalar expansion
is proportional to scalar expansion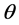 , which leads to the linear relationship between the metric potentials
, which leads to the linear relationship between the metric potentials 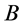 and
and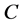 , that is,
, that is,
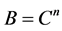 (23)
(23)
where 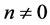 is a constant.
is a constant.
ii) With the help of special law of variation of Hubble’s parameter proposed by Berman [39] yields constant deceleration parameter models of the universe,
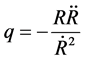 (24)
(24)
this admits the solution
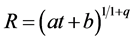 (25)
(25)
where 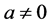 and
and ![]() are constants of integration.
are constants of integration.
This equation implies that the condition for accelerated expansion of universe is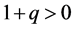 .
.
Now from Equations (16), (22), (23) and (25), we obtain
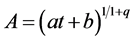 (26)
(26)
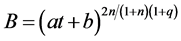 (27)
(27)
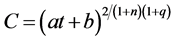 (28)
(28)
Now considering a well-accepted power law relation [40] -[42] between scale factor 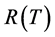 and scalar field
and scalar field 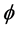 of the form
of the form
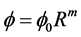 (29)
(29)
where ![]() is the constant of proportionality.
is the constant of proportionality.
Using Equation (23) in Equation (20), we obtain
Using this value of ![]() in Equations (26)-(28) and by a suitable choice of coordinates and constants (i.e. take
in Equations (26)-(28) and by a suitable choice of coordinates and constants (i.e. take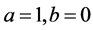 ), the metric (1) can be written as
), the metric (1) can be written as
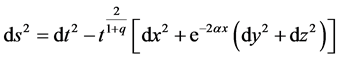 (30)
(30)
Further we find the volume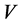 , mean Hubble parameter
, mean Hubble parameter![]() , expansion scalar
, expansion scalar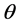 , shear scalar
, shear scalar![]() , and mean anisotropic parameter
, and mean anisotropic parameter 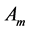 as
as
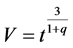 (31)
(31)
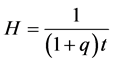 (32)
(32)
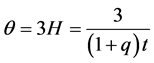 (33)
(33)
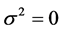 (34)
(34)
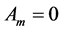 (35)
(35)
Using Equations (26)-(29), we get the energy density as
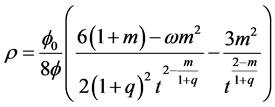 (36)
(36)
With the help of Equations (7) and (36), we get the pressure as
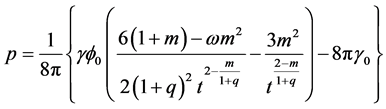 (37)
(37)
We observe that the scale factor 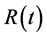 with respect to cosmic time grows rapidly as shown in Figure 1 while Figure 2 indicates that scalar field
with respect to cosmic time grows rapidly as shown in Figure 1 while Figure 2 indicates that scalar field 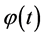 is increasing with evolution of universe. It can be easily seen from Figure 3 and Figure 4 that the volume goes on increasing as time increases and the energy density is decreasing function of time.
is increasing with evolution of universe. It can be easily seen from Figure 3 and Figure 4 that the volume goes on increasing as time increases and the energy density is decreasing function of time.
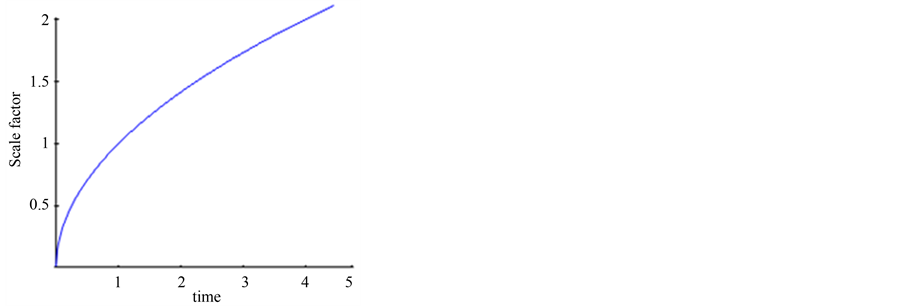
Figure 1. Scale factor versus time.
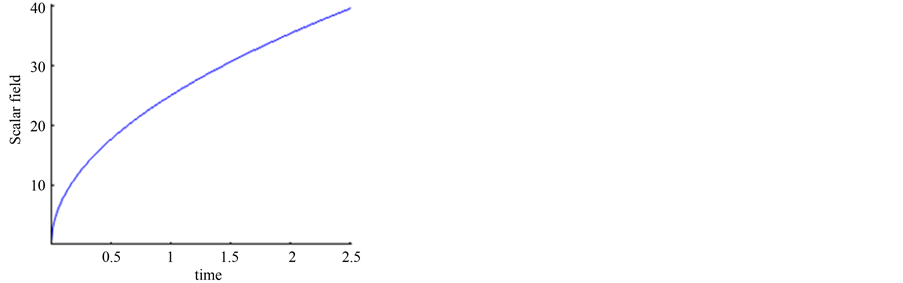
Figure 2. Scalar field versus time.
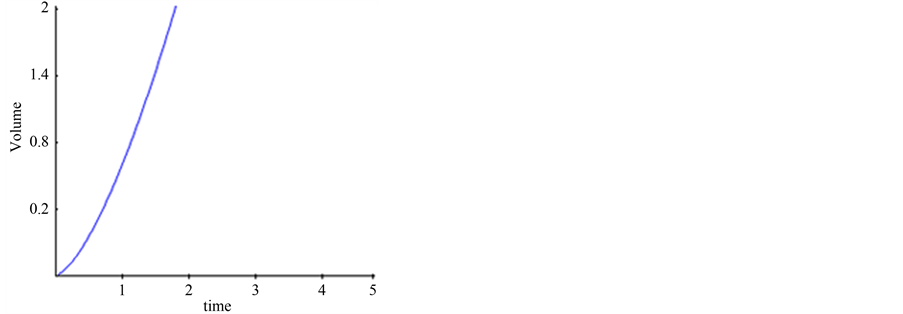
Figure 3. Volume versus time.
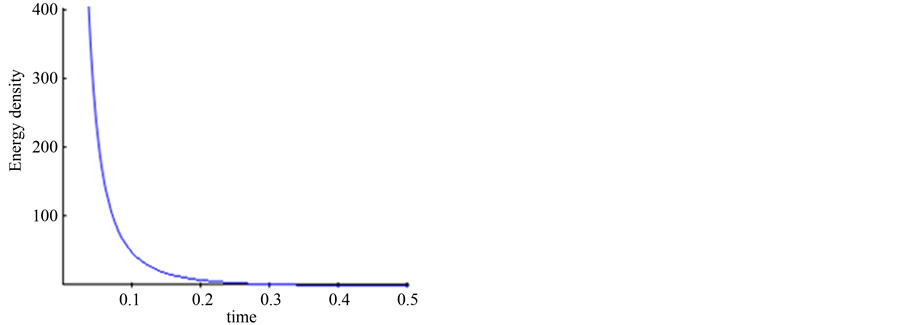
Figure 4. Energy density versus time.
4. Conclusion
In this paper, we have obtained Bianchi type  space-time with linear equation of state for perfect fluid in the Brans-Dicke theory. While solving Brans-Dicke’s field equations for Bianchi type
space-time with linear equation of state for perfect fluid in the Brans-Dicke theory. While solving Brans-Dicke’s field equations for Bianchi type  cosmological model, we have used a special law of variation of Hubble parameter proposed by Berman. It can also be observed that
cosmological model, we have used a special law of variation of Hubble parameter proposed by Berman. It can also be observed that  and
and ![]() decrease with time and approach zero as
decrease with time and approach zero as 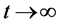 while they all become infinitely large as
while they all become infinitely large as 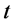 approaches zero. Also the model is expanding with time since
approaches zero. Also the model is expanding with time since 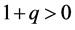 and it has initial singularity i.e. at
and it has initial singularity i.e. at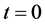 . It is also interesting to note that the average anisotropic parameter vanishes so that the model does not remain anisotropic throughout the evolution of the universe and the model becomes shear free. In this model the universe starts with finite volume and volume goes on increasing as time
. It is also interesting to note that the average anisotropic parameter vanishes so that the model does not remain anisotropic throughout the evolution of the universe and the model becomes shear free. In this model the universe starts with finite volume and volume goes on increasing as time 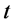 increases. Depending on the values of
increases. Depending on the values of 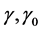 and other constant, the pressure is negative which works as dark energy. Also the generalized equation of state for
and other constant, the pressure is negative which works as dark energy. Also the generalized equation of state for 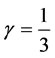 and
and 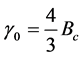 reduces to equation of state for strange quark matter.
reduces to equation of state for strange quark matter.
References
- Einstein, A. (1916) Die Grundlage der allgemeinen Relativitatstheorie. Annals of Physics, 49, 769-822.
- Jordan, P. (1955) Schwerkraft and Weltall. Friedch Vieweg and Sohn, Braunschweig, 207-213.
- Brans, C.H. and Dicke, R.H. (1961) Mach’s Principle and a Relativistic Theory of Gravitation. Physical Review, 24, 925-935. http://dx.doi.org/10.1103/PhysRev.124.925
- Nordtvedt, K. (1970) Post-Newtonian Metric for a General Class of Scalar-Tensor Gravitational Theories and Observational Consequences. The Astrophysical Journal, 161, 1059-1067. http://dx.doi.org/10.1086/150607
- Ross, D.K. (1972) Scalar-Tensor Theory of Gravitation. Physics Review D, 5, 284-289. http://dx.doi.org/10.1103/PhysRevD.5.284
- Schmidt, G., Greiner, W., Heinz, U. and Muller, B. (1981) Stability of Massive Objects in a New Scalar-Tensor Theory. Physical Review D, 24, 1484-1490. http://dx.doi.org/10.1103/PhysRevD.24.1484
- Singh, T. and Rai, L.N. (1983) Scalar Tensor Theories of Gravitation Foundations & Prospects. General Relativity and Gravitation, 15, 875-902. http://dx.doi.org/10.1007/BF00778798
- Nariai, H. (1972) Hamilton Approach to the Dynamics of Expanding Homogeneous Universe in the Brans-Dicke Cosmology. Progress of Theoretical Physics, 47, 1824-1843. http://dx.doi.org/10.1143/PTP.47.1824
- Reddy, D.R.K. and Rao, V.U.M. (1981) Field of Charged Particle in Brans-Dicke Theory of Gravitation. Journal of Physics: Mathematical and General, 14, 1973-1976. http://dx.doi.org/10.1088/0305-4470/14/8/021
- Banerjee, A. and Santos, N.O. (1982) Bianchi Type II Cosmological Models in Brans-Dicke Theory. Nuovo Cimento B, 67, 31-40. http://dx.doi.org/10.1007/BF02721068
- Singh, T., Rai, L.N. and Singh, T. (1983) An Anisotropic Cosmological Model in Brans-Dicke Theory. Astrophysics and Space Science, 96, 95-105. http://dx.doi.org/10.1007/BF00661944
- Ram, S. (1983) Spatially Homogeneous and Anisotropic Cosmology Solution in Brans-Dicke Theory. General Relativity and Gravitation, 15, 635-640. http://dx.doi.org/10.1007/BF00759040
- Ram, S. and Singh, D.K. (1984) LRS Bianchi Type-V Vacuum Cosmological Solution in Brans-Dicke Theory. Astrophysics and Space Science, 98, 193-196. http://dx.doi.org/10.1007/BF00651959
- Berman, M.S., Som, M.M. and Gomide, F.D. (1989) Brans-Dicke Static Universe. General Relativity and Gravitation, 21, 287-292. http://dx.doi.org/10.1007/BF00764101
- Reddy, D.R.K., Naidu, R.L. and Rao, V.U.M. (2007) A Cosmological Model with Negative Constant Deceleration Parameter in Brans-Dicke Theory. International Journal of Theoretical Physics, 46, 1443-1448. http://dx.doi.org/10.1007/s10773-006-9283-0
- Reddy, D.R.K. and Rao, N.V. (2001) Some Cosmological Model in Scalar Tensor Theory of Gravitation. Astrophysics and Space Science, 277, 461-472. http://dx.doi.org/10.1023/A:1012543323667
- Reddy, D.R.K. and Rao, M.V.S. (2006) A Cosmological Model with Negative Constant Deceleration Parameter in A Scalar-Tensor Theory. Astrophysics and Space Science, 306, 171-174. http://dx.doi.org/10.1007/s10509-006-9210-0
- Sáez, D. and Ballester, V.J. (1985) A Simple Coupling with Cosmological Implication. Physics Letters A, 113, 467-470. http://dx.doi.org/10.1016/0375-9601(86)90121-0
- Fransworth, D.L. (1967) Some New General Relativistic Dust Metrices Possessing String Isometrices. Journal of Mathematical Physics, 8, 2315-2317. http://dx.doi.org/10.1063/1.1705157
- Collins, C.B. (1974) Tilting at Cosmological Singularities. Communications in Mathematical Physics, 39, 131-151. http://dx.doi.org/10.1007/BF01608392
- Maartens, R. and Nel, S.D. (1978) Decomposable Differential Operators in a Cosmological Context. Communications in Mathematical Physics, 59, 273-283. http://dx.doi.org/10.1007/BF01611507
- Wainwright, J., Ince, W.C.W. and Marshman, B.J. (1979) Spatially Homogeneous and Inhomogeneous Cosmologies with Equation of State p=μ. General Relativity and Gravitation, 10, 259-271. http://dx.doi.org/10.1007/BF00759860
- Nayak, B.K. and Sahoo, B.K. (1989) Bianchi Type-V Models with a Matter Distribution Admitting Anisotropic Pressure and Heat Flow. General Relativity and Gravitation, 21, 211-225. http://dx.doi.org/10.1007/BF00764095
- Ram, S. (1990) Bianchi Type-V Perfect Fluid Space Times. International Journal of Theoretical Physics, 29, 901-906. http://dx.doi.org/10.1007/BF00675107
- Roy, S.R. and Singh, J.P. (1983) LRS Bianchi Type-V Universe Filled with Matter and Radiation. Astrophysics and Space Science, 96, 303-312. http://dx.doi.org/10.1007/BF00651674
- Roy, S.R. and Singh, J.P. (1985) A Bianchi Type-V Universe with Stiff Fluid and Electromagnetic Radiation. Australian Journal of Physics, 38, 763-768. http://dx.doi.org/10.1071/PH850763
- Banerjee, A. and Sanyal, A.K. (1988) Irrotational Bianchi Type-V Viscous Fluid Cosmology with Heat Flux. General Relativity and Gravitation, 20, 103-113. http://dx.doi.org/10.1007/BF00759320
- Coley, A.A. (1990) Bianchi V Imperfect Fluid Cosmology. General Relativity and Gravitation, 22, 3-18.
- Bali, R. and Singh, D.K. (2005) Bianchi Type-V Bulk Viscous Fluid String Dust Cosmological Model In General Relativity. Astrophysics and Space Science, 300, 387-394. http://dx.doi.org/10.1007/s10509-005-0152-8
- Bali, R. and Meena, B.L. (2004) Conformally Flat Tilted Bianchi Type-V Cosmological Models in General Relativity. Pramana, 62, 1007-1014. http://dx.doi.org/10.1007/BF02705248
- Bali, R. and Jain, S. (2007) The Bianchi Type-V Magnetized String Dust Cosmological Model in General Relativity. International Journal of Modern Physics D, 16, 1769-1781. http://dx.doi.org/10.1142/S0218271807011073
- Lorenz, D. (1981) An Exact Bianchi Type-V Tilted Cosmological Model with Matter and an Electromagnetic Field. General of Relativity and Gravitation, 13, 795-805. http://dx.doi.org/10.1007/BF00758217
- Singh, T. and Chaubey, R. (2006) Bianchi Type-V with a Perfect Fluid and A-Term. Pramana, 67, 415-428. http://dx.doi.org/10.1007/s12043-006-0002-4
- Singh, T. and Chaubey, R. (2006) Bianchi Type-V Universe with a Viscous Fluid and A-Term. Pramana, 68, 721-734. http://dx.doi.org/10.1007/s12043-007-0072-y
- Singh, J.K. (2007) Some Cosmological Models with Heat and Null Radiation Flow. Astrophysics and Space Science, 310, 241-244. http://dx.doi.org/10.1007/s10509-007-9505-9
- Singh, T. and Agrawal, A.K. (1993) Homogeneous Anisotropic Cosmological Models with Variable Gravitational and Cosmological “Constant”. International Journal of Theoretical Physics, 32, 1041-1059. http://dx.doi.org/10.1007/BF01215310
- Pradhan, A. and Yadav, V.K. (2002) Bulk Viscous Anisotropic Cosmological Models with Variable G and Λ. International Journal of Modern Physics D, 11, 893-912. http://dx.doi.org/10.1142/S0218271802002050
- Thirukkanesh, S. and Maharaj, S.D. (2008) Charged Anisotropic Matter with a Linear Equation of State. Classical and Quantum Gravity, 25, 235001.
- Berman, M.S. (1983) A Special Law of Variation for Hubble’s Parameter. Il Nuovo Cimento B, 74, 182-186. http://dx.doi.org/10.1007/BF02721676
- Pimentel, L.O. (1985) Exact Cosmological Solutions in Scalar-Tensor with Cosmological Constant. Astrophysics and Space Science, 112, 175-183. http://dx.doi.org/10.1007/BF00668418
- Johri, V.B. and Kalyani, D. (1994) Cosmological Models with Constant Deceleration Parameter in Brans-Dicke Theory. General Relativity and Gravitation, 26, 1217-1232. http://dx.doi.org/10.1007/BF02106714
- Ahmadi-Azar, E. and Riazi, N. (1995) A Class of Cosmological Solutions of Brans-Dicke Theory with Cosmological Constant. Astrophysics and Space Science, 226, 1-5. http://dx.doi.org/10.1007/BF00626893
NOTES
![]()
*Corresponding author.

