International Journal of Astronomy and Astrophysics
Vol.04 No.02(2014), Article ID:45885,7 pages
10.4236/ijaa.2014.42027
Einstein’s General Relativity and Pure Gravity in a Cosserat and De Sitter-Witten Spacetime Setting as the Explanation of Dark Energy and Cosmic Accelerated Expansion
Mohamed S. El Naschie
Department of Physics, University of Alexandria, Alexandria, Egypt
Email: chaossf@aol.com
Copyright © 2014 by author and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 13 February 2014; revised 10 March 2014; accepted 17 March 2014
ABSTRACT
Ordinary energy and dark energy density are determined using a Cosserat-Cartan and killing-Ya- no reinterpretation of Einstein’s special and general relativity. Thus starting from a maximally symmetric space with 528 killing vector fields corresponding to Witten’s five Branes model in ele- ven dimensional M-theory we reason that 504 of the 528 are essentially the components of the relevant killing-Yano tensor. In turn this tensor is related to hidden symmetries and torsional cou- pled stresses of the Cosserat micro-polar space as well as the Einstein-Cartan connection. Procee- ding in this way the dark energy density is found to be that of Einstein’s maximal energy mc2 where m is the mass and c is the speed of light multiplied with a Lorentz factor equal to the ratio of the 504 killing-Yano tensor and the 528 states maximally symmetric space. Thus we have E (dark) = mc2 (504/528) = mc2 (21/22) which is about 95.5% of the total maximal energy density in astounding agreement with COBE, WMAP and Planck cosmological measurements as well as the type 1a supernova analysis. Finally theory and results are validated via a related theory based on the degrees of freedom of pure gravity, the theory of nonlocal elasticity as well as ‘t Hooft-Veltman renormalization method.
Keywords:
General Relativity, Cosserat Micro-Polar Space, Dark Energy, Teleparellelism, Witten’s M-Theory, De Sitter Spacetime, Killing-Yano Tensor, Einstein-Cartan Relativity, Pure Gravity, Kaluza-Klein Theory, Nonlocal Elasticity, ‘t Hooft-Veltman Renormalization

1. Introduction
The aim of the present note is to demonstrate how easy it is to reformulate and rephrase Einstein’s general relativity [1] -[4] within the frame work of the theories of Cosserat, Cartan and Yano [2] - [9] to account for the obser- ved and quite surprising accelerated cosmological expansion of the universe and the concurrent conclusion that almost 95.5% of the total energy density of the universe seems to be negative dark energy [10] - [27] . In addition we attack the problem from a related point of view based on the degrees of freedom of pure gravity as well as nonlocal elasticity reaching the same results and conclusions [28] - [44] . In particular we show that ‘t Hooft-Velt- man-Wilson dimensional regularization implies fractal-Cantorian space which can have many common features with K. Eringen nonlocal elasticity [44] .
2. Analysis
We start from the premise that both Einstein’s spacetime and the maximally symmetric Witten’s five Branes model leads to the same Lorentzian factor γ = 1 for the maximal Einstein energy density, E = γmc2 where m is the mass and c is the speed of light and will look upon Cartan’s affine connection from a Lie symmetry groups view point [1] -[5] . Never the less the trivial identity
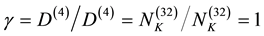 (1)
(1)
where γ is the Lorentz factor, 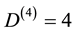 and
and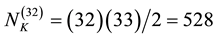 , implies a far more intricate relation than the deceptively harmless appearance transpires [5] - [9] . The rationale behind this assertion is that exactly 504 of the 528 particle-like quantum states may be at least heuristically identified as Cartan-like torsional states. This could be deduced with relative ease from an educated counting exercise of the quantum states of Heterotic string theory [5] . In the course of doing that it will become clear that the 504 are the internal killing-Yano hidden dimensions of E8E8 exceptional Lie symmetry group of superstrings plus 8 [5] :
, implies a far more intricate relation than the deceptively harmless appearance transpires [5] - [9] . The rationale behind this assertion is that exactly 504 of the 528 particle-like quantum states may be at least heuristically identified as Cartan-like torsional states. This could be deduced with relative ease from an educated counting exercise of the quantum states of Heterotic string theory [5] . In the course of doing that it will become clear that the 504 are the internal killing-Yano hidden dimensions of E8E8 exceptional Lie symmetry group of superstrings plus 8 [5] :
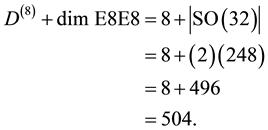 (2)
(2)
The 528 killing vector fields on the other hand are interpreted by us here in two ways. First it is the number of components of the killing-Yano conformal tensor [25] and second it is the sum of the dimensions of E8, E7, E6, E5 and E4 [10] - [12] . Based on its Dykin diagram E5 is just another name for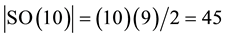 . In other words we have [10] - [13]
. In other words we have [10] - [13]
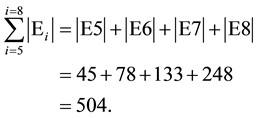 (3)
(3)
Adding |E4| = 24 where |E4| is simply another name for |SU(5)| of GUT unification [11] - [13] , we see that
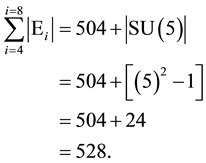 (4)
(4)
In other words we have [7] - [9]
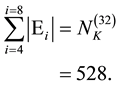 (5)
(5)
Consequently the number of the killing components [25] [26] which are related to the purely “ordinary” energy are given by
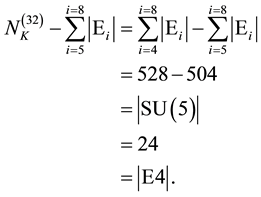 (6)
(6)
It is vital at this point not to confuse dark energy with torsion energy due to the 24 Riemann-Cartan connection components in four dimensions because the concept torsion has various meanings in string theory compared to Einstein-Cartan theory [26] . In the present work the 4.5% cosmically measured ordinary energy density is due to the 24 Yano-killing tensor components [25] while the conjectured dark energy is due to the 504 rest components known from the spectrum of Heterotic string theory [5] .
Two further relevant observations regarding the vital number 24. First it is exactly equal to the number of the gauge bosons of SU(5) GUT unification which adds 12 bosons to the well known and experimentally found 12 bosons of the SU(3) SU(2) U(1) standard model of high energy physics [2] [7] [28] [29] . Second the only pure number in the killing-Yano totally skew symmetric tensor of the well known 5 expression is 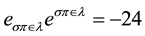 [25] .
[25] .
Contemplating the situation a little it is not particularly difficult to convince oneself that the Lorentzian factor of Einstein’s energy density corresponding to 24 non-trivial Bianchi identities [2] [26] is the ratio between the 24 and the Witten bulk of 528 maximally symmetric space [2] . Consequently ordinary energy comes with a Lorentzian factor [14] - [23]
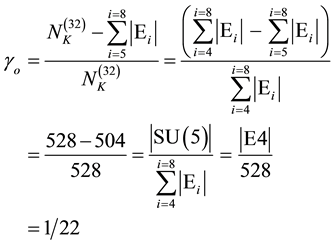 (7)
(7)
and therefore ordinary is given by [14] - [22]
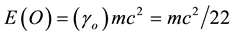 (8)
(8)
Exactly as expected from previous analysis. Note that 22 could be interpreted as the number of two forms, i.e. harmonic forms of a K3 Kähler compactification representing nontrivial deformations of the anti-symmetric string tensor. Dark energy on the other hand is squarely connected to the negative energy of the non-vanishing torsional part in the Cartan connection, namely the 504 known also from the particle physics spectroscopy of Heterotic string theory [5] . The corresponding Lorentzian factor is thus a ratio representing a coupling constant between two sectors
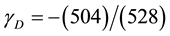 (9)
(9)
leading to a dark energy density [14] - [22]
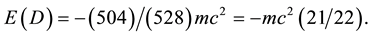 (10)
(10)
Einstein’s energy density 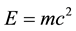 on the other hand is blind to the preceding fine distinction which wrongly considers
on the other hand is blind to the preceding fine distinction which wrongly considers  completely equivalent to
completely equivalent to

We note on passing that 528 is divided in Witten’s model into 1D strings, 2D membranes and 5D Branes [2] [7] [8] :

The corresponding E8E8 expression includes the point-like particles as well as the 3D and 4D Branes [2] [7] - [9] :

The hidden Yano-killing 504 on the other hand are given in Heterotic super string theory by three groups of states, namely 480, 16 and 8 leading to [5]

and

as explained in great detail in [5] . We also note that 




exist [5] . For an in depth study of the E-line exceptional Lie symmetry groups at the root of the present theory Refs. [30] - [32] could be considerably helpful. It may come as a pleasant surprise to the reader to see the power of the imaginative idea of fractal-Cantorian geometry which ascribes the origin of gravity, quantum entanglement, dark energy etc. to the topology of fractal Cantor set to see the entire preceding analysis reduced that way to a single simple equation. The equation is the ratio of either the entangled 4 dimensional spacetime dimension, i.e. 








3. Nonlocal Elasticity and Dark Energy
Unlike the engineering theories of elasticity and elastoplastic structures as well as the theory of micropolar media, there is no meaning at all for the rotation of a point in the Riemannian geometry of Einstein’s field equation. Consequently the details of the energy household are glossed over by taking the continuum limit. That way the role of anticlastic curvature as well as shear forces and torsional deformation is not brought to the fore [35] - [37] .
The preceding analysis is intended to rectify the situation and may be seen as a Cosserat-like material space based analysis in the spirit of the analogies discussed in connection with the pinched elastic cylindrical shell and the corresponding anti-curvature caused by local curvature [23] . We stress that the failure of Einstein’s general relativity to predict dark energy directly could easily be explained via the Cosserat-like theory presented here [23] [24] and even more directly by a careful analysis of the vacuum state of Einstein’s field equation which is usually referred to as pure gravity as we will do shortly in the next section. However we must mention that first Einstein and then Cartan were aware of the problem of rotation and torsion and proposed what became known later on as the Teleparallelism theory [24] [27] . Thus our Cosserat-like theory points essentially in the same general direction as the Teleparallelism relativity theory [24] [27] . It should not pass unnoticed that 





which is essentially the Magueijo-Smolin ingenious extension of Einstein’s celebrated formula. Needless to say, this result agrees completely with our derivation as shown in detail in earlier publications in the present journal [10] [21] .
4. Dark Energy from Pure Gravity
Deriving dark energy from pure gravity [33] [34] , i.e. starting from Einstein’s field equation in the absence of a matter field might be surprising but it is essentially the same as that starting from special relativity. Both approaches have something fundamental in common, namely the geometry and topology of spacetime without matter playing any direct fundamental role. In this sense our present treatment is similar to that of A. Zakharov’s approach to gravity [33] [38] . The crucial fundamental equation in our analysis is that relating the degrees of freedom of the vacuum state to the dimension. The derivation of this equation is quite complex and involved several Lagrangian multiplier but the final result is disarmingly simple, namely [33] [34]

where D are the degrees of freedom and d is the dimension. Since Einstein’s formula 




Consequently α could be regarded as the scaling exponent 


The Equation (16) for D well deserves a closer look as there is more to it than meets the eyes. Setting 




5. Conclusions
Whether we look upon the problem of dark energy exclusively from the point of view of the special theory of relativity or exclusively from the view point of pure energy of general relativity, the end result is the same. As many leading scientists such as Nobel Laureate G. ‘t Hooft [39] [40] maintained, without detailed geometrical topological analysis of spacetime, dark energy and cosmic expansion cannot be explained satisfactorily. The vacuum is far more real and fundamental than any physical theory ever supposed. It essentially gives rise to both gravity and quantum mechanics [10] - [12] [14] [19] [33] [34] [38] . This is a view shared by many experts on the subject [41] .
Finally nothing could testify to the power of the fractal Cantorian picture of spacetime as the origin of all fundamental physics more than the agreement of the cosmological measurements of COBE, WMAP and type 1a supernova measurement with the results of our equation 
sity is given by 




Acknowledgements
The Author is indebted for the constructive suggestions and criticisms of an anonymous Referee. He is also deeply thankful to Prof. Dr. Dr. Otto Bruhns who communicated to me some exceptionally relevant papers by our common teacher, the eminent Prof. Dr. Dr. T. Lehmann. Prof. Lehmann was the first to formulate the theory of elasticity in Einstein’s four dimensional spacetime. Memories of our student years in the sixties of last century in Hannover, Germany are highly treasured.
References
- Duff, M.J. (1999) The World in Eleven Dimensions. Instute of Physical Publications, Bristol.
- Penrose, R. (2004) The Road to Reality. Jonathan Cape, London.
- Cartan, E. (1926) Espaces á connexion affine, projective et conforme. Acta Mathematica, 48, 4-42.
- Czajko, J. (2004) Elie Cartan and Pan-Geometry of Multispatial Hyperspace. Chaos, Solitons & Fractals, 19, 479-502. http://dx.doi.org/10.1016/S0960-0779(03)00254-6
- Kaku, M. (1999) Introduction to Superstrings and M-Theory. Springer, New York. http://dx.doi.org/10.1007/978-1-4612-0543-2
- Becker, K., Becker, M. and Schwarz, J.H. (2007) String Theory and M-Theory. Cambridge University Press, Cambridge.
- El Naschie, M.S. (2009) On the Witten-Duff Five Branes Model Together with Knots Theory and E8E8 Superstrings in a Single Fractal Spacetime Theory. Chaos, Solitons & Fractals, 41, 2016-2021. http://dx.doi.org/10.1016/j.chaos.2008.08.005
- El Naschie, M.S. (2008) Using Witten’s Five Brane Theory and the Holographic Principle to Derive the Value of the Electromagnetic Fine Structure Constant
= 1/137. Chaos, Solitons & Fractals, 38, 1051-1053. >http://html.scirp.org/file/2-4500293x68.png" class="200" />= 1/137. Chaos, Solitons & Fractals, 38, 1051-1053. http://dx.doi.org/10.1016/j.chaos.2008.06.001
- El Naschie, M.S. (2008) Fuzzy Knot Theory Interpretation of Yang-Mills Instantons and Witten’s 5 Brane Model. Chaos, Solitons & Fractals, 38, 1349-1354. http://dx.doi.org/10.1016/j.chaos.2008.07.002
- He, J.-H. and Marek-Crnjac, L. (2013) The Quintessence of El Naschie’s Theory of Fractal Relativity and Dark Energy. Fractal Spacetime & Noncommutative Geometry in Quantum & High Energy Physics, 3, 130-137.
- Helal, M.A., Marek-Crnjac, L. and He, J.-H. (2013) The Three Page Guide to the Most Important Results of M.S. El Naschie’s Research in E-Infinity and Quantum Physics and Cosmology. Open Journal of Microphysics, 3, 141-145. http://dx.doi.org/10.4236/ojm.2013.34020
- Marek-Crnjac, L. (2013) An Invitation to El Naschie’s Theory of Cantorian Spacetime and Dark Energy. International Journal of Astronomy and Astrophysics, 3, 464-471. http://dx.doi.org/10.4236/ijaa.2013.34053
- El Naschie, M.S. (2009) The Theory of Cantorian Spacetime and High Energy Particle Physics (an Informal Review). Chaos, Solitons & Fractals, 41, 2635-2646. http://dx.doi.org/10.1016/j.chaos.2008.09.059
- El Naschie, M.S. (2013) Experimentally Based Theoretical Arguments That Unruh’s Temperature, Hawkings’s Vacu- um Fluctuation and Rindler’s Wedge Are Physically Real. American Journal of Modern Physics, 2, 357-361. http://dx.doi.org/10.11648/j.ajmp.20130206.23
- El Naschie, M.S. and Helal, A. (2013) Dark Energy Explained via the Hawking-Hartle Quantum Wave and the Topolo- gy of Cosmic Crystallography. International Journal of Astronomy and Astrophysics, 3, 318-343. http://dx.doi.org/10.4236/ijaa.2013.33037
- El Naschie, M.S. (2014) Dark Energy Explained via Quantum Field Theory in Curved Spacetime. Journal of Modern Physics and Applications, 2, 1-7.
- El Naschie, M.S. (2013) The Missing Dark Energy of the Cosmos from Light Cone Topological Velocity and Scaling the Planck Scale. Open Journal of Microphysics, 3, 64-70. http://dx.doi.org/10.4236/ojm.2013.33012
- El Naschie, M.S. (2013) Topological-Geometrical and Physical Interpretation of the Dark Energy of the Cosmos as a “Halo” Energy of the Schrödinger Quantum Wave. Journal of Modern Physics, 4, 591-596. http://dx.doi.org/10.4236/jmp.2013.45084
- El Naschie, M.S. (2013) A Rindler-KAM Spacetime Geometry and Scaling the Planck Scale Solves Quantum Relativity and Explains Dark Energy. International Journal of Astronomy and Astrophysics, 3, 483-493. http://dx.doi.org/10.4236/ijaa.2013.34056
- El Naschie, M.S. (2013) From Yang-Mills Photon in Curved Spacetime to Dark Energy Density. Journal of Quantum Information Science, 3, 121-126. http://dx.doi.org/10.4236/jqis.2013.34016
- Marek-Crnjac, L., et al. (2013) Chaotic Fractal Tiling for the Missing Dark Energy and Veneziano Model. Applied Mathematics, 4, 22-29. http://dx.doi.org/10.4236/am.2013.411A2005
- Hehl, F. (1968) Space-Time as Generalized Cosserat Coninuum. In: Kronev, E., Ed., Mechanics of Generalized Continua, Springer Verlag, Berlin, 347-349. http://dx.doi.org/10.1007/978-3-662-30257-6_43
- El Naschie, M.S. (2013) Nash Embedding of Witten’s M-Theory and Hawking-Hartle Quantum Wave of Dark Energy. Journal of Modern Physics, 4, 1417-1428. http://dx.doi.org/10.4236/jmp.2013.410170
- Geng, C.-Q., Lee, C.-C., Saridakis, E.N. and Wu, Y.-P. (2011) “Teleparallel” Dark Energy. Physics Letters B, 704, 384-387.
- Frolov, V. and Zelnikov, A. (2013) Introduction to Black Hole Physics. Oxford University Press, Oxford.
- Hehl, F. and Obukhov, Y. (2007) Elie Cartan’s Torsion in Geometry and in Field Theory: An Essay. Annales de la Foundation Louis de Broglie, 32, 38 p.
- Burnett, J., Chervova, O. and Vassiliev, D. (2009) Dirac Equation as a Special Case of Cosserat Elasticity. In: Cialdea, A., Lanzara, F. and Ricci, P.E., Eds., Analysis, Partial Differential Equations and Applications―The Vladimir Maz’ya Anniversary Volume, Series Operator Theory: Advances and Applications, Vol. 193, Birkhauser Verlag, 15-29.
- El Naschie, M.S. (2007) SU(5) Grand Unification in a Transfinite Form. Chaos, Solitons & Fractals, 32, 370-374. http://dx.doi.org/10.1016/j.chaos.2006.09.018
- El Naschie, M.S. (2007) SO(10) Grand Unification in a Fuzzy Setting. Chaos, Solitons & Fractals, 32, 958-961. http://dx.doi.org/10.1016/j.chaos.2006.09.068
- El Naschie, M.S. (2008) High Energy Physics and the Standard Model from Exceptional Lie Groups. Chaos, Solitons & Fractals, 36, 1-17. http://dx.doi.org/10.1016/j.chaos.2007.08.058
- El Naschie, M.S. (2008) Symmetry Groups Pre-Requisite for E-Infinity in High Energy Physics. Chaos, Solitons & Fractals, 35, 202-211. http://dx.doi.org/10.1016/j.chaos.2007.05.006
- El Naschie, M.S. (2008) Notes on Exceptional Lie Symmetry Groups Hierarchy and Possible Implications for E-Infinity High Energy Physics. Chaos, Solitons & Fractals, 35, 69-70.
- Duff, M. and von Nieuwenhuizen, P. (1980) Quantum Inequivalence of Different Field Representation. Phys. Ltts, 94B, 179-182. http://dx.doi.org/10.1016/0370-2693(80)90852-7
- Duff, M.J. (1999) The World in Eleven Dimensions. Institute of Physics Publications, Bristol.
- El Naschie, M.S. (1990) Stress, Stability and Chaos in Structural Engineering: An Energy Approach. McGraw-Hill International Editions: Civil Engineering Series, London, Tokyo.
- El Naschie, M.S. (1979) Die Ableitung einer Kosistenten Schalentheorie aud dem dreidimensionalen Kontinuum. Ōsterreichische Ingenieur-Zeitshift (Austrian Engineering Journal), 22, 339-344.
- El Naschie, M.S. (1974) The Role of Formulation in Elastic Buckling. Ph.D. Thesis, Civil Engineering Department, University College, University of London, April.
- El Naschie, M.S. (2006) Is Einstein’s General Field Equation More Fundamental than Quantum Field and Particle Physics? Chaos, Solitons & Fractals, 30, 525-531. http://dx.doi.org/10.1016/j.chaos.2005.04.123
- Fry, A.B. (2010) CERN, Dark Energy and Dark Matter. Lindau Nobel Online Community, July 1. Lindau.nature.com/Lindau/2010/07/com-dark-energy-and-dark-matter/
- Musser, G. (2013) Does Some Deeper Level of Physics Underlie Quantum Mechanics? An Interview with Nobelist Gerard ’t Hooft. Scientific American, October 7.
- Gao, S. (2013) Explaining Holographic Dark Energy. Galaxies, 1, 180-191. http://dx.doi.org/10.3390/galaxies1030180
- ’t Hooft, G. (2001) A Confrontation with Infinity. In: Sidharth, B. and Altaisky, M., Eds., Frontiers of Fundamental Physics 4, Kluwer-Plenum, New York, 1-12. http://dx.doi.org/10.1007/978-1-4615-1339-1_1
- El Naschie, M.S. (2001) ’t Hooft’s Dimensional Regularization Implies Transfinite Heterotic String Theory and Dimensional Transmutation. In: Sidharth, B. and Altaisky, M., Eds., Frontiers of Fundamental Physics 4, Kluwer-Ple- num, New York, 81-86. http://dx.doi.org/10.1007/978-1-4615-1339-1_7
- Challamel, N., Wang, C.M. and Elishakoff, I. (2014) Discrete Systems Behave as Nonlocal Structural Elements: Bending, Buckling and Vibration Analysis. European Journal of Mechanic-A/Solids, 44, 125-135. http://dx.doi.org/10.1016/j.euromechsol.2013.10.007



 = 1/137. Chaos, Solitons & Fractals, 38, 1051-1053. >http://html.scirp.org/file/2-4500293x68.png" class="200" />= 1/137. Chaos, Solitons & Fractals, 38, 1051-1053.
= 1/137. Chaos, Solitons & Fractals, 38, 1051-1053. >http://html.scirp.org/file/2-4500293x68.png" class="200" />= 1/137. Chaos, Solitons & Fractals, 38, 1051-1053.