International Journal of Astronomy and Astrophysics
Vol. 3 No. 2A (2013) , Article ID: 32995 , 12 pages DOI:10.4236/ijaa.2013.32A002
Transfer Trajectory Design for Mars Exploration
School of Aeronautics Science and Engineering, Beihang University, Beijing, China
Email: lvjing@buaa.edu.cn
Copyright © 2013 Jing Lü et al. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Received February 26, 2013; revised March 28, 2013; accepted April 5, 2013
Keywords: Invariant Manifolds; Differential Correction Method; Lyapunov Orbit; Aerobraking; Rotating and Static Atmospheric Environments
ABSTRACT
With regard to the human exploration of Mars, low energy transfer trajectory is designed for Mars exploration based on the combination of invariant manifolds, differential correction and aerobraking methods. The whole transfer trajectory is composed of four stages: 1) from the Earth parking orbit to the Lyapunov orbit around Lagrange point L2 in the SunEarth system; 2) from the Lyapunov orbit around L2 to the Lyapunov orbit around L1 in the Sun-Mars system; 3) from the Lyapunov orbit around L1 in the Sun-Mars system to the large elliptical orbit around Mars; and 4) from the large elliptical orbit around Mars to the near-Mars parking orbit. In the first three stages, the circular restricted three-body problem is considered, and the trajectory is designed by using invariant manifolds and the differential correction method. The simulation results show that the transfer trajectory designed by means of the invariant manifolds of the Lyapunov orbit costs lower energy and shorter time of flight than that designed by means of the invariant manifold of the Halo orbit. In the fourth stage, the two-body problem is considered, and the aerobraking method is applied. A comparative performance analysis of static and rotating atmospheric models is carried out by using the details of duration, aerodynamic loading of the Mars vehicle, and other orbital parameters. It is shown that, on the low periareon where the influence of the atmospheric density increases, the changes of orbit parameters between rotating and static atmospheric environments are in large difference, such as orbital semimajor axis, orbital eccentricity, and so on. The influence of Martian rotating atmospheric environment should be considered.
1. Introduction
Beginning in the 1960s, the former Soviet Union and the United States have both repeatedly carried out successful launches of Mars vehicles and, thus, obtained an enriching experience in deep space exploration. However, China’s advent to the technological exploration of Mars is still in a developmental stage, with preliminary proposals that engineering research of deep space exploration would materialize within the next ten years. With the smooth progress of China’s exploration of the Moon, it is expected that exploration of Mars will also make it to the research agenda. Traditionally, the dynamical basis of the two-body problem, through the patched conic method, has been used for preliminary design of interplanetary trajectories, but this method consumes large energy. To satisfy rendezvous constraints and reduce maneuever costs to acceptable levels, techniques such as gravity assists and, more recently, low thrust trajectories are now being investigated. In addition, in the past few decades, mission scenarios have increased in complexity and science goals require an expansion of the solution space. For example, trajectory designers have explored three-body techniques to develop missions to the vicinity of the Lagrange points, such mission scenarios are impossible to model accurately in the two-body problem.
The circular restricted three-body problem (CR3BP) is known to have five equilibrium points. It was Lagrange, in 1772, who first identified all five equilibrium points in the CR3BP, the three collinear points (also described by Euler in 1772) and two equilateral points, hence, they are usually denoted the Lagrange points [1]. Research during the early part of the twentieth century in the determination of periodic orbits and the advent of modern computers led to the launch of the ISEE-3 spacecraft in1978. The vehicle was subsequently inserted into a halo orbit in the vicinity of L1 Sun-Earth Lagrange point [2,3]. Since ISEE-3, a number of other missions to the vicinity of the Lagrange points have successfully been completed [4-9]. The most recent major advancement in the use of CR3BP trajectory design tools, Martin Lo et al. proposed a concept that Interplanetary Superhighway(IPS) [10-14], in 1995- 1998. Their works evidenced the importance of the invariant manifolds associated to the periodic orbits around Lagrange points, that using these invariant manifolds design the transfer trajectories between two planets can save a lot of energy. Howell designed the transfer trajectories from Earth parking orbits to L1 or L2 halo orbits by using the manifolds of halo orbits [15]. Belbruno designed the transfer trajectories from Sun-perturbed earthto-moon by using manifolds of halo orbits [16]. German and Frabcesco designed the transfer trajectories for planets by using the invariant manifolds of halo orbits [17,18]. Xuming applied the invariant manifolds of Lyapunov orbit to achieve the quick transfer to the distant retrograde orbit in Earth-Moon system [19]. MJ Capinski focused on Lyapunov orbits at L2 and transversal intersections of invariant manifolds in the Jupiter-Sun CR3BP [20]. Llibre J found out homoclinic orbits using transversality of the invariant manifolds associated to the Lyapunov family of periodic orbits near L2 in CR3BP [21]. Baoyin focused on trajectories from the Lagrange points and their Lyapunov orbits that can access the entire surfaces of the primary bodies for the sun-Earth and Earth-moon systems [22]. Gong designed the low-energy lunar landing trajectory using the invariant manifolds of halo orbits [23]. From the above, the invariant manifolds of halo orbits and Lyapunov orbits are applied to design the transfer trajectories for planets, and the invariant manifolds of halo orbits have been used to transfer from a Sun-Earth halo orbit to a Sun-Mars halo orbit in the literature. For Earth and Mars are almost coplanar planets, the invariant manifolds of Lyapunov orbits are used to design the transfer trajectories for Mars exploration in this paper, and the four-body problem consisted of SunEarth-Mars-vehicle is decomposed into two coplanar circular restricted three-body problem, Sun-Earth-vehicle and Sun-Mars-vehicle.
Aerobraking method is always adopted when designing the transfer trajectory from the large elliptical orbit around the Mars to near-Mars parking orbit. Aerocapture can be classified into single and multiple crossings. Because a single crossing through the atmosphere requires a more precise angle of incidence and greater energy, in engineering practice, there is a tendency to generally employ multiple crossings through the atmosphere. The research results present resulted in the published literature [24,25]. On exploration and orbit capture for Mars have all been based on premise that the Martian atmosphere is static. In fact, the Martian atmosphere is rotating. When studying the influence of the Earth’s external rotation atmosphere on the orbit of Earth’s satellites, the rotational angular velocity of the atmosphere is considered to be equal to the angular velocity of Earth’s rotation.
With increased proximity to Earth, the satellite would be more apparently affected by the rotating atmosphere [26]. So, the influence of the Martian external rotation atmosphere will be studied in this paper.
In this paper, low energy transfer trajectory is designed for Mars exploration based on combination of invariant manifolds, differential correction and aerobraking methods. The whole transfer trajectory is divided into four stages. The first three stages, the part of transfer trajectory from Earth parking orbit to L2 Lyapunov orbit in Sun-Earth system, the part of transfer trajectory from L2 Lyapunov orbit in Sun-Earth system to L1 Lyapunov orbit in Sun-Mars system and the part of transfer trajectory from L1 Lyapunov orbit in Sun-Earth system to the large elliptical orbit around the Mars, are designed applying invariant manifolds of Lyapunov orbit and differential correction method. The fourth stage, the part of transfer trajectory from the large elliptical orbit around the Mars to near-Mars parking orbit, is designed by the aerobraking method, and the effect of Martian rotating atmosphere is considered. Moreover, the premise in the second stage is the same as the work of German [17], which is that the Sun-Earth-Mars-vehicle four-body problem is decomposed into two coplanar circular restricted three-body problems. To compare with German’s work, transfer trajectory designed using the invariant manifolds of Lyapunov orbit costs lower energy and shorter time of flight than the one which is designed using the invariant manifold of Halo orbit. The premise in the fourth stage is that the rotational angular velocity of the external rotational atmosphere of Mars is equal to the rotation angular velocity of Mars. The results indicate that the influence of the rotating atmosphere should be taken into full consideration when the periareon is low.
2. Transfer Trajectory Design Based on Invariant Manifolds and Differential Correction Method
Figure 1 shows the whole transfer trajectory from Earth to Mars, which is divided into four stages: 1) the part of

Figure1. Earth-to-Mars transfer concept.
transfer trajectory from Earth parking orbit to L2 Lyapunov orbit in Sun-Earth system; 2) the part of transfer trajectory from L2 Lyapunov orbit in Sun-Earth system to L1 Lyapunov orbit in Sun-Mars system; 3) the part of transfer trajectory from L1 Lyapunov orbit in Sun-Earth system to the large elliptical orbit around the Mars; 4) and the part of transfer trajectory from the large elliptical orbit around the Mars to near-Mars parking orbit. In this section, the circular restricted three-body problem is considered. Using invariant manifolds of Lyapunov orbits around Lagrange points in Sun-Earth system and SunMars system, the first three steps of low energy transfer trajectory are designed.
2.1. Equations of Motion
Consider a vehicle P of negligible mass move under the gravitational influence of two masses P1 and P2, referred to as the primary masses, or simply the primaries. P1 and P2 have masses m1 and , with a unique parameter
, with a unique parameter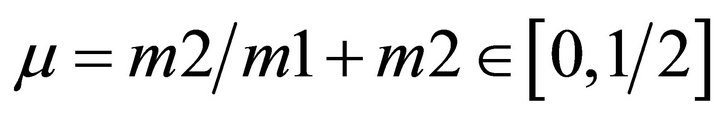 . Assume that P1 and P2 have circular orbits about their common center of mass. The vehicle P is free to move in the plane defined by the circular orbits of the primaries, but cannot affect their motion. In the usual rotating coordinate system, the origin is located at the mass center of primaries P1 and P2. The x-axis is always directed from the larger toward the smaller primary. The y-axis is 90˚ from the x-axis in the primary plane of motion. The z-axis completes the right handed system, defining the out of plane direction. To simplify the equations of motion, let us take the units of mass, length, and time, such that the sum of the masses of primaries P1 and P2, the distance between the primaries, the gravitational constant, and the period of the primaries are 1, 1, 1, and 2π, respectively.
. Assume that P1 and P2 have circular orbits about their common center of mass. The vehicle P is free to move in the plane defined by the circular orbits of the primaries, but cannot affect their motion. In the usual rotating coordinate system, the origin is located at the mass center of primaries P1 and P2. The x-axis is always directed from the larger toward the smaller primary. The y-axis is 90˚ from the x-axis in the primary plane of motion. The z-axis completes the right handed system, defining the out of plane direction. To simplify the equations of motion, let us take the units of mass, length, and time, such that the sum of the masses of primaries P1 and P2, the distance between the primaries, the gravitational constant, and the period of the primaries are 1, 1, 1, and 2π, respectively.
Let 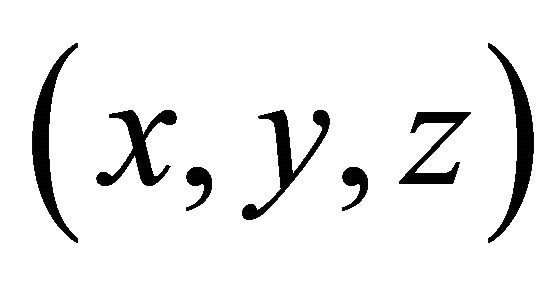 be the position of the vehicle, the equations of motion can be written as
be the position of the vehicle, the equations of motion can be written as
 (1)
(1)
where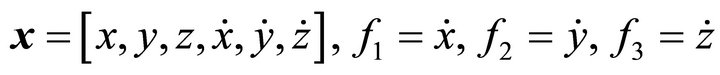 ,
,
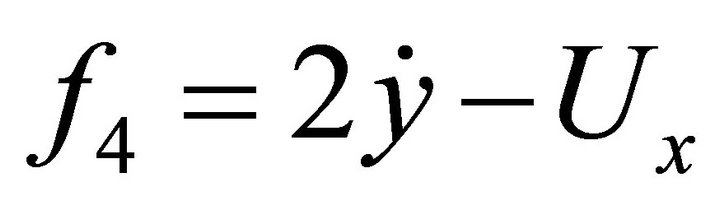 ,
, 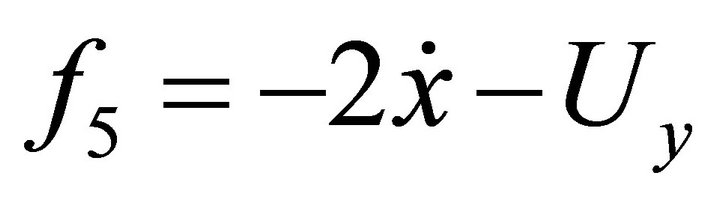 ,
,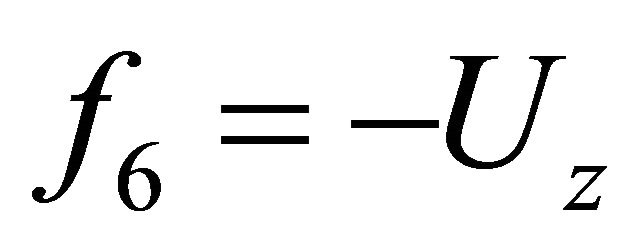 .
.
In the equations above, U can be written as follows
 (2)
(2)
where
 .
.
2.2. Lyapunov Orbit
In accordance with the Lindstedt-Poincare method, Richardson got third-order approximation of periodic or quasi-periodic orbits as [27]
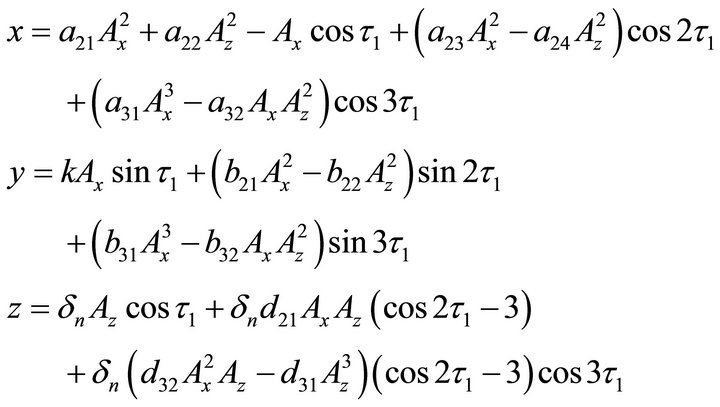 (3)
(3)
where Ax and Az represent the amplitudes in x direction and z direction respectively, in addition, 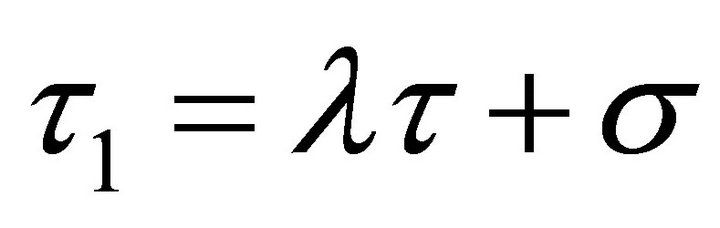 ,
, 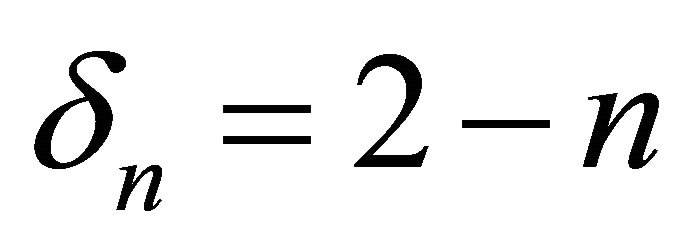 , where σ represents the phase angle of xy, λ represents frequency factor, τ represents the time of periodic orbit, other parameters can be seen in literature [27]. Since Lyapunov orbits are located on the x-y plane, third-order expansions of Lyapunov orbit can be obtained after substituting Az = 0 into the Equation (3).
, where σ represents the phase angle of xy, λ represents frequency factor, τ represents the time of periodic orbit, other parameters can be seen in literature [27]. Since Lyapunov orbits are located on the x-y plane, third-order expansions of Lyapunov orbit can be obtained after substituting Az = 0 into the Equation (3).
For third-order approximations are insufficient for serious study of accurate motion, analytical approximations must be combined with differential correction process to generate a Lyapunov orbit accurate enough for mission design. Initial conditions are chosen on the x-axis, and can be written as . The equations of motion are integrated until the trajectory crosses the xyplane, then the time when crossing occurs are expressed as ε,
. The equations of motion are integrated until the trajectory crosses the xyplane, then the time when crossing occurs are expressed as ε, 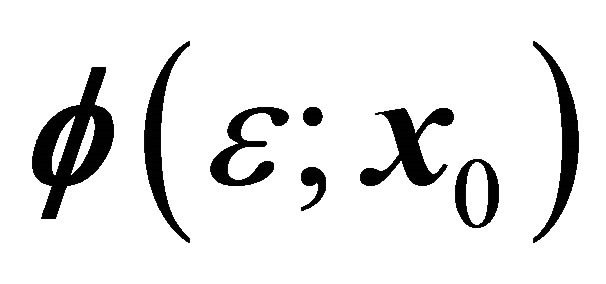 denotes the trajectory. To produce a Lyapunov orbit, a perpendicular crossing is needed, and so the target state vector needs to have the form
denotes the trajectory. To produce a Lyapunov orbit, a perpendicular crossing is needed, and so the target state vector needs to have the form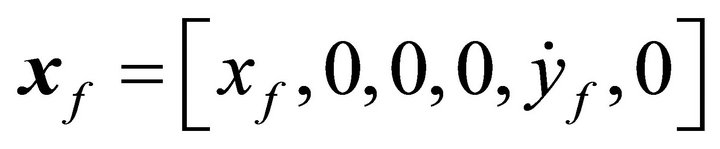 . By adjusting the initial variables
. By adjusting the initial variables 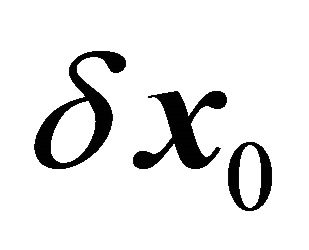 and
and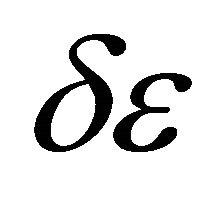 , the final values
, the final values  and yf can be driven to zero.
and yf can be driven to zero.
The difference of final states is written as following
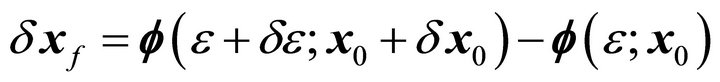 (4)
(4)
Using the Taylor expansion Method and ignoring the higher-order term
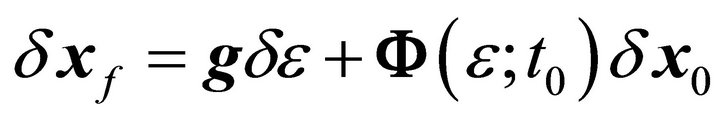 (5)
(5)
where  and
and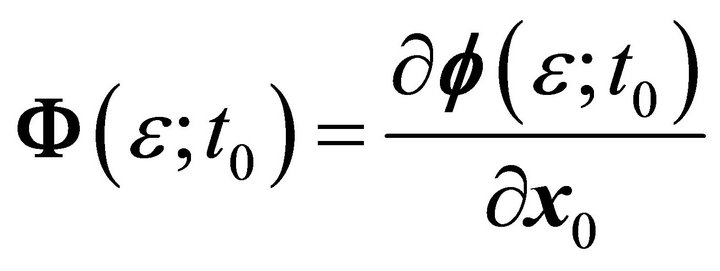 . So, the differential variables
. So, the differential variables 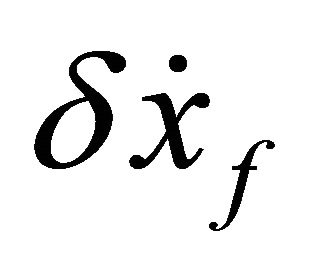 and
and 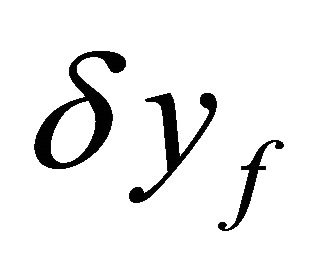 can be expressed as
can be expressed as
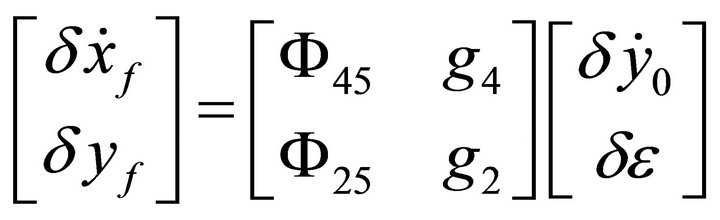 (6)
(6)
The state transition matrix can be computed numerically by integrating simultaneously the following equations
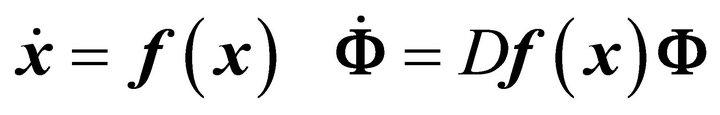 (7)
(7)
with initial conditions

where Df(x) represents the Jacobian matrix,  represents the 6 × 6 identity matrix.
represents the 6 × 6 identity matrix.
The iteration process will be continue until 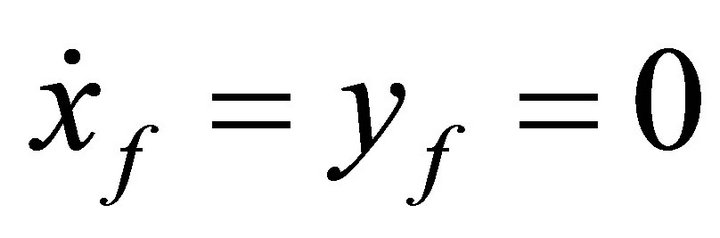 , within some acceptable tolerance. Then, combining third order approximation and differential correction, we can get sufficient accurate Lyapunov orbits around L1 in Sun-Earth system and L2 in Sun-Mars system.
, within some acceptable tolerance. Then, combining third order approximation and differential correction, we can get sufficient accurate Lyapunov orbits around L1 in Sun-Earth system and L2 in Sun-Mars system.
2.3. Invariant Manifolds of Lyapunov Orbit
The computation of the stable and unstable manifolds associated with a Lyapunov orbit can be accomplished numerically. The procedure is based on the monodromy matrix  which is the state transition matrix after one period of a Lyapunov orbit. The characteristics of the local geometry of the phase space can be determined from the eigenvalues and eigenvectors of the monodromy matrix [14]. The eigenvectors can then be used in approximating the local invariant manifolds near any point along the Lyapunov orbit. Let Ys and Yu denotes the stable and unstable eigenvector of the monodromy matrix at a point X0 respectively. The initial values of the stable manifold and unstable manifold can be written as following, respectively. The initial guess of the stable manifold and unstable manifold can be written as following
which is the state transition matrix after one period of a Lyapunov orbit. The characteristics of the local geometry of the phase space can be determined from the eigenvalues and eigenvectors of the monodromy matrix [14]. The eigenvectors can then be used in approximating the local invariant manifolds near any point along the Lyapunov orbit. Let Ys and Yu denotes the stable and unstable eigenvector of the monodromy matrix at a point X0 respectively. The initial values of the stable manifold and unstable manifold can be written as following, respectively. The initial guess of the stable manifold and unstable manifold can be written as following
 (8)
(8)
where  represents a micro constants.
represents a micro constants.
By integrating the motion Equation (1) forward with the initial conditions of the stable manifold, we generate the stable manifold tube. By integrating the motion Equation (1) backward with the initial conditions of the unstable manifold, we generate the unstable manifold tube. The results are shown in Figures 2-5.
From the simulation results in Figures 2-5, it can be seen that the expand direction of stable or unstable manifold is different if the positive and negative sign of the micro constant  is changed.
is changed.
2.4. Trajectory Design from Earth Parking Orbit to Large Elliptical Orbit around Mars
Based on invariant manifolds and differential correction method, we can design the transfer trajectories from Earth parking orbit to large elliptical orbit around Mars. To link two specific points, a differential correction method is usually employed in designing intermediate transfer orbit [28]. The initial position and velocity, the time of flight (TOF), and the final position are specified, the initial position and velocity are the numerically propagated for the given TOF and a state transition matrix relating the initial and final positions and velocities is computed.
 (a) Lyapunov orbit and left part of stable manifold (d < 0)
(a) Lyapunov orbit and left part of stable manifold (d < 0)
 (b) Lyapunov orbit and right part of stable manifold (d > 0)
(b) Lyapunov orbit and right part of stable manifold (d > 0)
Figure 2. Stable manifold associated with Lyapunov orbit around L2 in Sun-Earth system.
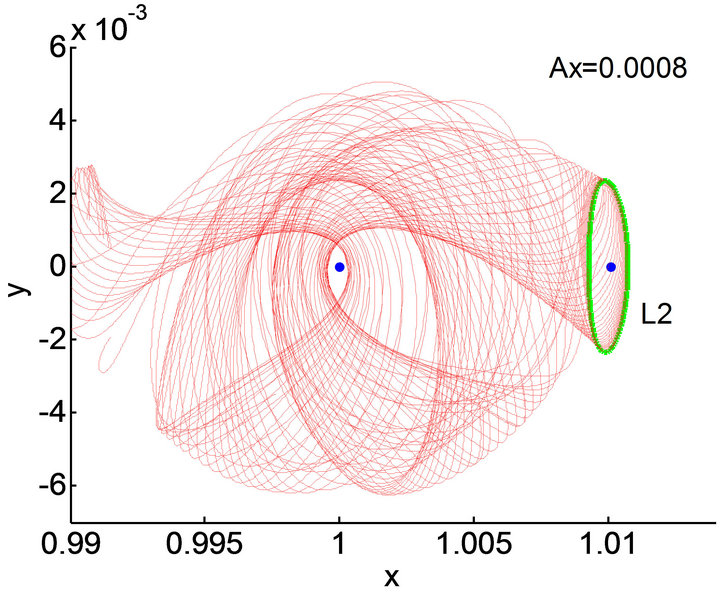 (a) Lyapunov orbit and left part of stable manifold (d < 0)
(a) Lyapunov orbit and left part of stable manifold (d < 0)
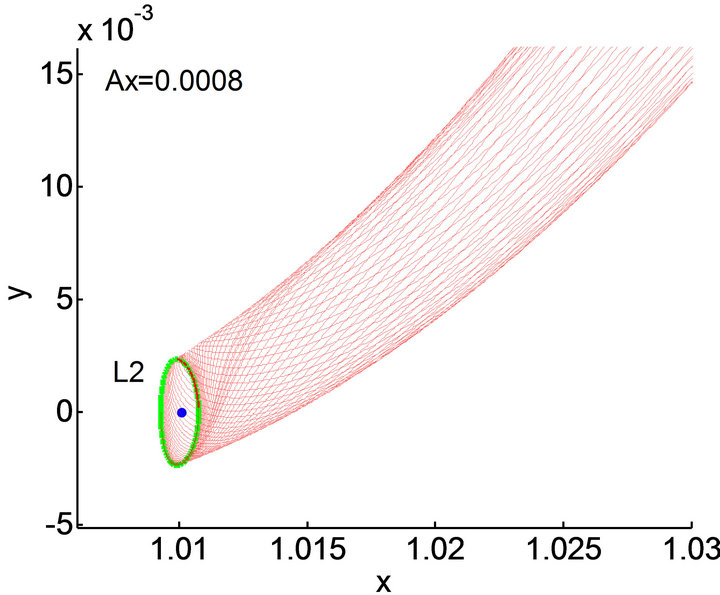 (b) Lyapunov orbit and right part of stable manifold (d > 0)
(b) Lyapunov orbit and right part of stable manifold (d > 0)
Figure 3. Unstable manifold associated with Lyapunov orbit around L2 in Sun-Earth system.
 (a) Lyapunov orbit and left part of stable manifold (d < 0)
(a) Lyapunov orbit and left part of stable manifold (d < 0)
 (b) Lyapunov orbit and right part of stable manifold (d > 0)
(b) Lyapunov orbit and right part of stable manifold (d > 0)
Figure 4. Stable manifold associated with Lyapunov orbit around L1 in Sun-Mars system.
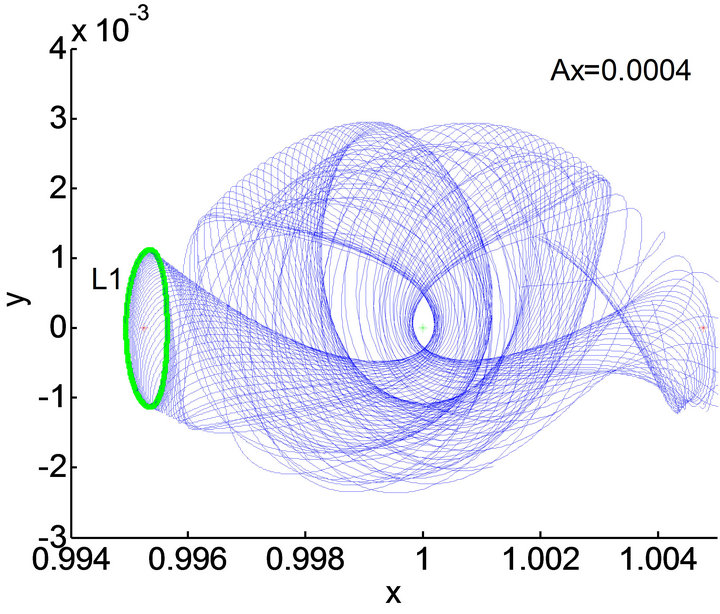 (a) Lyapunov orbit and left part of unstable manifold (d < 0)
(a) Lyapunov orbit and left part of unstable manifold (d < 0)
 (b) Lyapunov orbit and right part of unstable manifold (d > 0)
(b) Lyapunov orbit and right part of unstable manifold (d > 0)
Figure 5. Unstable manifold associated with Lyapunov orbit around L1 in Sun-Mars system.
 and
and 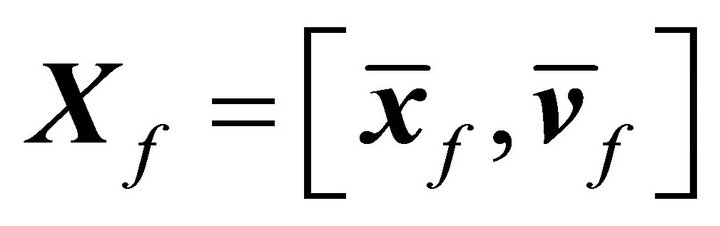 denote the initial state and the target state respectively. Since Lyapunov orbits locate on the x-y plane,
denote the initial state and the target state respectively. Since Lyapunov orbits locate on the x-y plane,  and
and 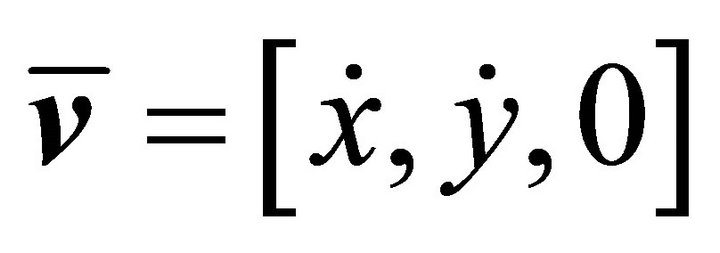 .
.  can be obtained from the following equation
can be obtained from the following equation
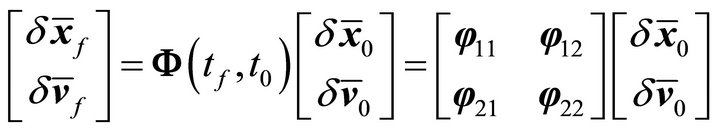 (9)
(9)
where the 6 × 6 matrix 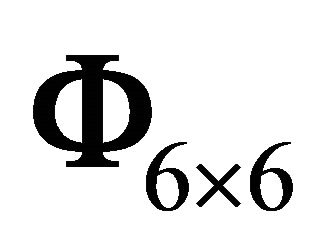 has been decomposed into four 3 × 3 submatrices, tf and t0 represents the final TOF and the initial TOF respectively.
has been decomposed into four 3 × 3 submatrices, tf and t0 represents the final TOF and the initial TOF respectively.
Note that, for the Equation (9), 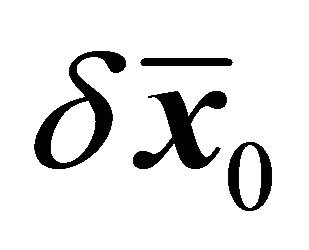 is assumed to be equal to zero because the initial position is fixed. Then it is used with the 3 × 3 matrix
is assumed to be equal to zero because the initial position is fixed. Then it is used with the 3 × 3 matrix  to update the initial velocity to reach the desired final location, that is
to update the initial velocity to reach the desired final location, that is
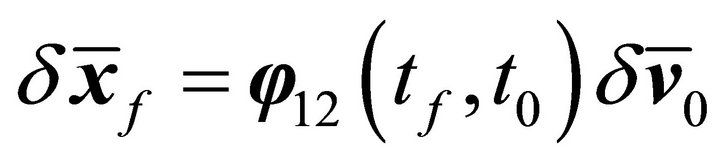 (10)
(10)
Usually, convergence to a solution is achieved within a few iterations.
2.4.1. Transfer Trajectory from Earth Parking Orbit to Lyapunov Orbit around L2 in Sun-Earth System
In this paper, the amplitude of L2 Lyapunov orbit in Sun-Earth system is . It can be seen that the expand directions of invariant manifolds depend on the value of d, as illustrated in Figure 2. So, the stable manifold of L2 Lyapunov orbit in the Sun-Earth System which corresponds to the condition of
. It can be seen that the expand directions of invariant manifolds depend on the value of d, as illustrated in Figure 2. So, the stable manifold of L2 Lyapunov orbit in the Sun-Earth System which corresponds to the condition of  is selected. Afterwards, the manifold which is nearest to earth parking orbit is chosen as the standard manifold (as shown in Figure 6). According to the literatures [28,29], it indicates that the vehicle can enter the glide status earlier, which is advantageous to continuous working for payload, when a certain point on the manifold is picked as the initial point, therefore, we choose point A on the standard manifold as the initial point of the transfer trajectory, and a point on the parking orbit which orbit altitude is 200 km is selected as the target point B, in the end, we connect the orbits using the differential correction method. During this process, the integration should proceed backwards with respect to time. The simulation results is shown in the Figure 7, to minimize the energy consumption that from the Earth parking orbit to the stable manifold, we should make the angle between the vehicle’s velocity vector on the intermediate transfer trajectory at point B and the vehicle’s velocity vector on the Earth parking orbit at point B equal to zero, so we choose the 1857th point (point A) on stable manifold as the initial point, the flight time from the earth parking orbit to the stable manifold is 23.35 d, and the energy consumption is 4.223 km/s.
is selected. Afterwards, the manifold which is nearest to earth parking orbit is chosen as the standard manifold (as shown in Figure 6). According to the literatures [28,29], it indicates that the vehicle can enter the glide status earlier, which is advantageous to continuous working for payload, when a certain point on the manifold is picked as the initial point, therefore, we choose point A on the standard manifold as the initial point of the transfer trajectory, and a point on the parking orbit which orbit altitude is 200 km is selected as the target point B, in the end, we connect the orbits using the differential correction method. During this process, the integration should proceed backwards with respect to time. The simulation results is shown in the Figure 7, to minimize the energy consumption that from the Earth parking orbit to the stable manifold, we should make the angle between the vehicle’s velocity vector on the intermediate transfer trajectory at point B and the vehicle’s velocity vector on the Earth parking orbit at point B equal to zero, so we choose the 1857th point (point A) on stable manifold as the initial point, the flight time from the earth parking orbit to the stable manifold is 23.35 d, and the energy consumption is 4.223 km/s.
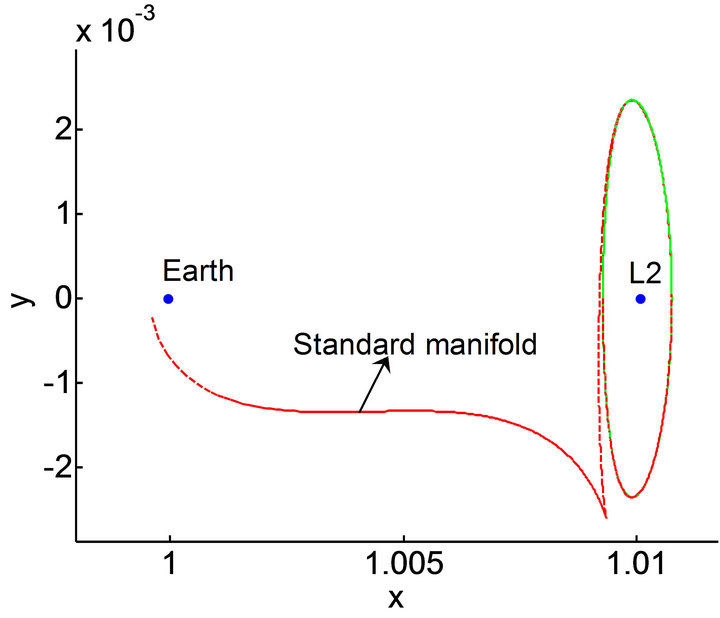
Figure 6. Standard manifold in Sun-Earth system.

Figure 7. Transfer trajectory designed by differential correction process.
2.4.2. Transfer Trajectory between the Sun-Earth L2 Lyapunov Orbit and the Sun-Mars L1 Lyapunov Orbit
German and Frabcesco indicated that two-Circular Restricted three-body problems (CR3BP), having small mass parameters, do not allow the manifolds to develop for enough in order to approach each other, in more refined models contemplating the full solar system dynamics, a closer approach or even an intersection, after thousands of years, may occur [17,18]. Because mass parameters of Sun-Earth system and Sun-Mars system are equal to 3.036 ×10−6 and 3.229 ×10−7 respectively, unstable manifolds of L2  of the Sun-Earth system will not intersects with stable manifolds of L1
of the Sun-Earth system will not intersects with stable manifolds of L1  in the Sun-Mars system. To accomplish the L2 in Sun-Earth system to L1 in the Sun-Mars system transfer, an intermediate transfer orbit should be designed.
in the Sun-Mars system. To accomplish the L2 in Sun-Earth system to L1 in the Sun-Mars system transfer, an intermediate transfer orbit should be designed.
In this paper, the amplitude of L2 Lyapunov orbit of Sun-Earth system is , and the amplitude of L1 Lyapunov orbit of Sun-Mars system is
, and the amplitude of L1 Lyapunov orbit of Sun-Mars system is . First, we should attempt to determine the two trajectories, which are on unstable manifold of L2 Lyapunov orbit of Sun-Earth system and stable manifold of L1 Lyapunov orbit of Sun-Mars system respectively, most closely approach each other, called the standard manifolds. Then we selected the appropriate initial angle of location the earth relative to Mars, here the angle is
. First, we should attempt to determine the two trajectories, which are on unstable manifold of L2 Lyapunov orbit of Sun-Earth system and stable manifold of L1 Lyapunov orbit of Sun-Mars system respectively, most closely approach each other, called the standard manifolds. Then we selected the appropriate initial angle of location the earth relative to Mars, here the angle is .
.
Case 1: Design of transfer trajectory in Sun-Earth system
First, we convert the stable manifold associated with the Sun-Mars L1 Lyapunov orbit to the Sun-Earth rotating coordinate system. Then, we connect the initial point A on the unstable manifold of the Sun-Earth L2 Lyapunov orbit and the target point B on the stable manifold of the Sun-Mars L1 Lyapunov orbit using the differential correction method, as shown in Figure 8. To minimize the energy consumption that from the unstable manifold of the Sun-Earth L2 Lyapunov orbit to the stable manifold of the Sun-Mars L1 Lyapunov orbit, we should make the angle between the vehicle’s velocity vector on the intermediate transfer trajectory at point B and the vehicle’s velocity vector on the stable manifold at point B should equal to zero, so we select the 1857th point (point B) on the stable manifold of L1 Lyapunov orbit in Sun-Mars system as the target point, in this process the fight time is 181.5 d. Table 1 shows the comparison results of intermediate transfer trajectory for Mars exploration, one is designed using invariant manifold of Lyapunov orbit, and the other is designed using invariant manifold of Halo orbit. From the comparison result, it can be seen that the costs in terms of ΔV using invariant manifold of Lyapunov orbit to design transfer trajectory is 3.78% less than the ones using halo orbit, and the time of flight using invariant manifold of Lyapunov orbit to design transfer trajectory is 23.02% less than the one using halo orbit.

Figure 8. Transfer trajectory designed in Sun-Earth rotating coordinate system.

Table 1. Cost comparison for design transfer trajectorybetween L2 in the Sun-Earth system and L1 in the Sun-Earth system.
Case 2: Design of transfer trajectory in Sun-Mars system
First, the unstable manifold of the Sun-Earth L2 Lyapunov orbit is converted to the Sun-Mars rotating coordinate system. Let point A on the stable manifold of the Sun-Mars L1 Lyapunov orbit is chosen as the initial point, and point B on the unstable manifold of the SunEarth L2 Lyapunov orbit is chosen as the target point. The intermediate transfer trajectory is designed to connect the initial point A and the target point B using the differential correction method, as shown in Figure 9. During this process, the integration should proceed backwards with respect to time. To minimize the energy consumption that from the unstable manifold of the SunEarth L2 Lyapunov orbit to the stable manifold of the Sun-Mars L1 Lyapunov orbit, we should make the angle between the vehicle’s velocity vector on the intermediate transfer trajectory at point B and the vehicle’s velocity vector on the unstable manifold at point B should equal to zero, so we select the 971th point on the unstable manifold of L2 Lyapunov orbit in Sun-Earth system as the target point B, and this process the fight time is 219.4d. Table 2 shows that the costs in terms of ΔV using invariant manifold of Lyapunov orbit to design transfer trajectory is 9.32% less than the one using halo orbit, and the time of flight using invariant manifold of Lyapunov orbit to design transfer trajectory is 23.02% less than the one using halo orbit.

Figure 9. Transfer trajectory designed in Sun-Mars rotating coordinate system.

Table 2. Cost comparison for design transfer trajectorybetween L2 in the Sun-Earth system and L1 in the Sun-Mars system.
2.4.3. Transfer Trajectory from the Sun-Mars L1 Lyapunov Orbits to the Large Elliptical Orbit around the Mars
As shown in Figure 5, we can see that expansion direction of the manifold depend on the positive and negative sign of d. So, the unstable manifold of the Sun-Mars L1 Lyapunov orbit which corresponds to  is selected. For the amplitude of L1 Lyapunov orbit in Sun-Mars system is
is selected. For the amplitude of L1 Lyapunov orbit in Sun-Mars system is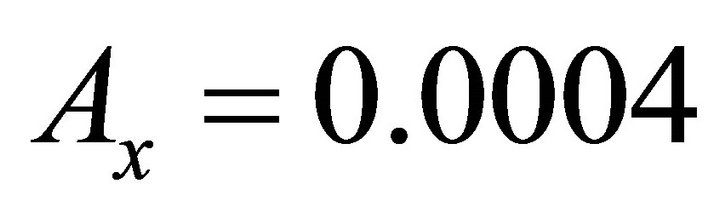 , the closet distance between the unstable manifolds of L1 Lyapunov orbit and Mars is 4107.6 km.
, the closet distance between the unstable manifolds of L1 Lyapunov orbit and Mars is 4107.6 km.
Note that the aerobraking method will be applied to design the transfer trajectory from the large elliptical orbit around the Mars to near-Mars parking orbit. In this paper, the apareon of the large elliptical selected is 50,000 km, so the manifolds of L1 Lyapunov orbit whose amplitude is 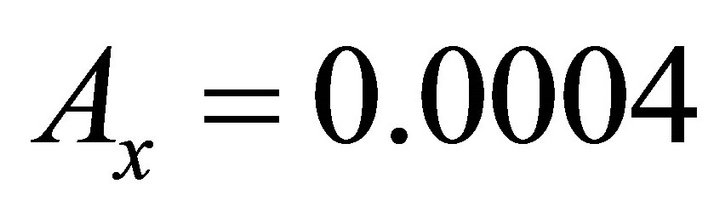 can reach the apareon of the large elliptical orbit around the Mars, and a maneuver is needed to adjust the vehicle’s velocity vector on the apareon when the manifolds intersect the large elliptical orbit to make the vehicle from the manifolds to the large elliptical orbit around the Mars, this stage need not to use the differential correction method. In the simulation from L1 Lyapunov orbits to the Large elliptical orbit around the Mars, the flight time is 276.8 d, the energy consumption is 3.246 km/s.
can reach the apareon of the large elliptical orbit around the Mars, and a maneuver is needed to adjust the vehicle’s velocity vector on the apareon when the manifolds intersect the large elliptical orbit to make the vehicle from the manifolds to the large elliptical orbit around the Mars, this stage need not to use the differential correction method. In the simulation from L1 Lyapunov orbits to the Large elliptical orbit around the Mars, the flight time is 276.8 d, the energy consumption is 3.246 km/s.
3. Transfer Trajectory Design Based on Aerobraking Method
In this section, the two-body problem is considered. Based on aerobraking, the transfer trajectory from the large elliptical orbit around the Mars to near-Mars parking orbit is designed, as shown as Figure 1. This study establishes the dynamics equations for the Mars vehicle, both in the static and rotating atmospheric environment. A comparative performance analysis of atmospheric models was carried out using details of the duration, aerodynamic loading of the Mars vehicle, and other orbital parameters.
3.1. Equations of Motion
Let us set the inertial coordinates of Mars as OXYZ. The origin O is right at the center of mass of Mars and XY plane is the equatorial plane of Mars; the x-axis indicates the direction of periareon whereas the z-axis indicates the direction of rotation of Mars. The y-axis, x-axis, and z-axis form a right-handed system. After the Mars vehicle crosses through the atmosphere, the kinetic vector equation can be written as follows
 (11)
(11)
where D, L and G represent the atmospheric drag vector, the atmospheric lift vector, and the gravity vector acting on the Mars vehicle, respectively; r is the distant vector from the Mars vehicle to the center of Mars.
The atmospheric lift acceleration vector, the atmospheric drag acceleration vector, and gravity acceleration of the Mars vehicle are expressed, respectively, as
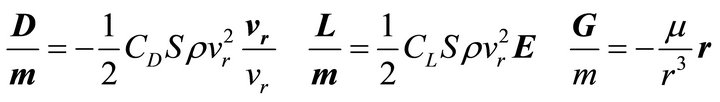 (12)
(12)
where CL and CD represent the coefficient of the atmospheric lift and the atmospheric drag, respectively; S and m represents the area and the mass of the Mars vehicle, respectively; vr represents the velocity vector of the Mars vehicle in relation to the atmosphere, where , v is the velocity vector of the Mars vehicle in the inertial coordinate of Mars, and vg is the velocity vector of the atmosphere in the inertial coordinate of Mars. Moreover,
, v is the velocity vector of the Mars vehicle in the inertial coordinate of Mars, and vg is the velocity vector of the atmosphere in the inertial coordinate of Mars. Moreover, 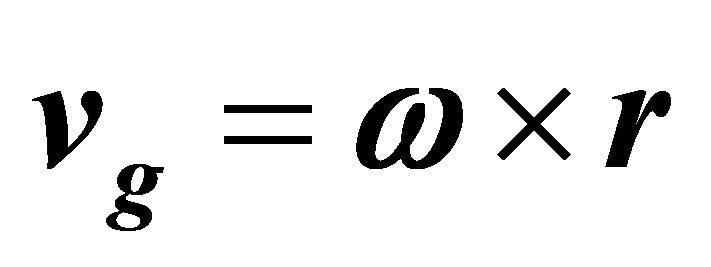 , where
, where  is the angular velocity vector of Mars. Otherwise, the atmospheric density of the external rotation atmosphere of Mars can be expressed as [24]
is the angular velocity vector of Mars. Otherwise, the atmospheric density of the external rotation atmosphere of Mars can be expressed as [24]
 (13)
(13)
where H stands for the height of the orbit that the Mars vehicle occupies. In addition, the E in Equation (12) can also be written as following
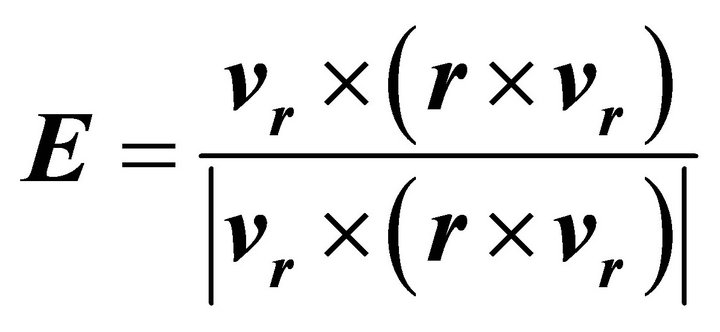 (14)
(14)
By factoring Equations (12)-(14) into Equation (11), the motion equation of the Mars vehicle in the inertial coordinate of Mars can be obtained.
3.2. Simulation and Analysis
The results of this study can be considered on the basis of the differences in the results of simulation, shown in the dynamics equation, of the Mars vehicle when subjected to two types of atmospheres. The initial position of the Mars vehicle is the apareon; the other initial parameters are shown in Table 3. The initial velocity of the Mars vehicle can be written as:
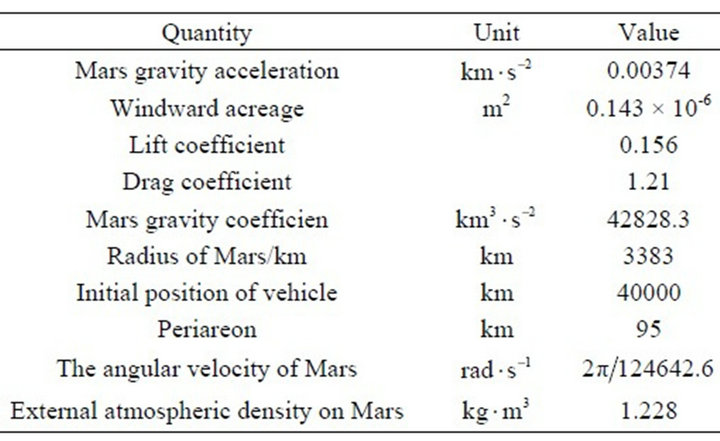
Table 3. Initial parameters.
 (15)
(15)
In this equation, e is the orbital eccentricity and a is the semimajor axis of the orbit.
Case 1: Comparison of orbital parameters
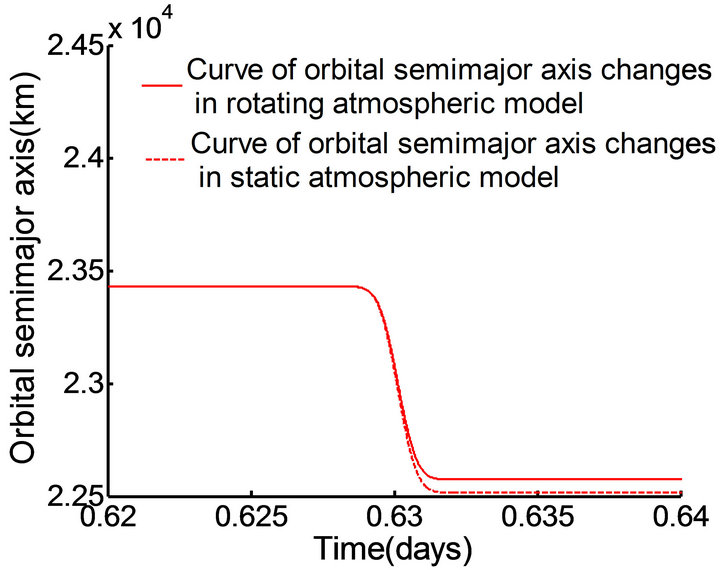
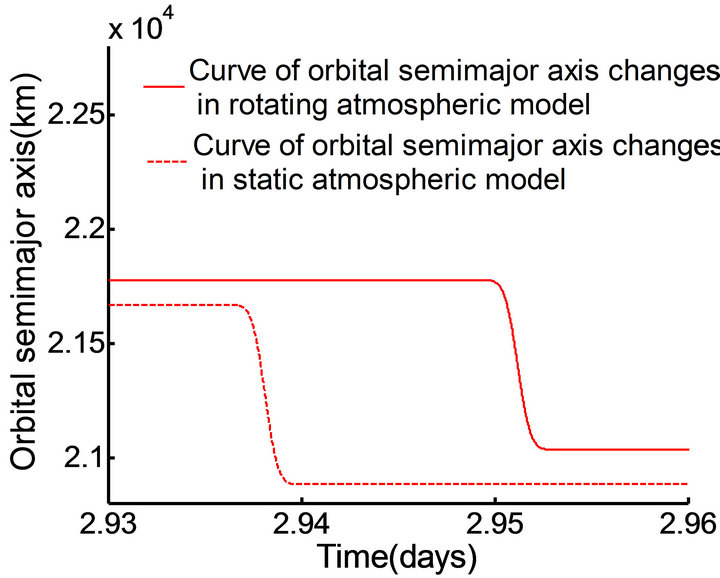
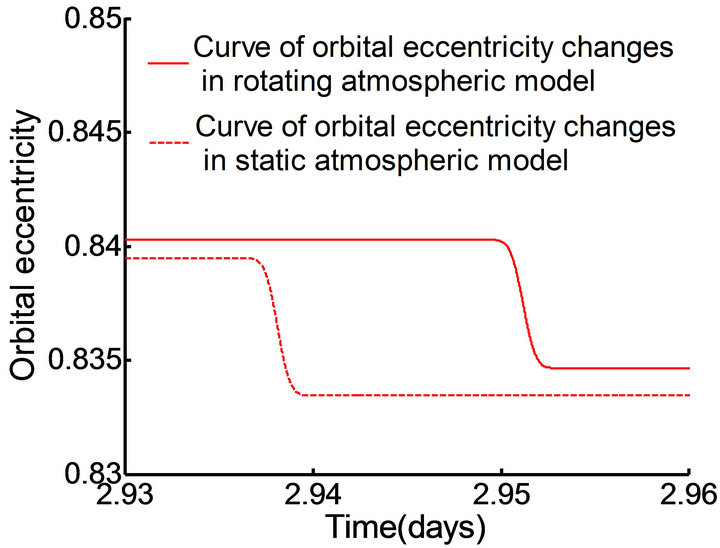
In this case, the orbit inclination is set to 3.9653˚and the longitude of the ascending node of the orbit is 0.573˚, other initial parameters are presented in Table 3. From the simulation results shown in Figures 10 and 11, it can be seen that with multiple crossings of the Mars vehicle through the atmosphere, the disparity of changes in the orbital semimajor axis and the orbital eccentricity in the two atmospheric models is small; however, in the rotating atmosphere model, the change in the cycle of the
 (a) The first time crossing through the atmosphere
(a) The first time crossing through the atmosphere
 (b) The second time crossing through the atmosphere
(b) The second time crossing through the atmosphere
 (c) The third time crossing through the atmosphere
(c) The third time crossing through the atmosphere
Figure 10. The curve of semi-major axis changes in different time periods.
 (a) The first time crossing through the atmosphere
(a) The first time crossing through the atmosphere
 (b) The second time crossing through the atmosphere
(b) The second time crossing through the atmosphere
 (c) The third time crossing through the atmosphere
(c) The third time crossing through the atmosphere
Figure 11. The curve of orbital eccentricity changes in different time periods.
orbital semimajor axis a and the orbital eccentricity e becomes longer, compared with that in the static atmospheric model; this marks the emergence of “hysteresis”. Thus, it is evident that the rotating atmospheric model influences the time that the Mars vehicle reach the target orbit.
The simulation results shown in Figures 12 and 13 validate the accuracy of the Gaussian perturbation theory [25], which holds that the change of the orbital inclination  and the longitude of the ascending node of the orbit
and the longitude of the ascending node of the orbit  are zero in the static atmosphere model; in the rotating atmospheric model, the orbital inclination
are zero in the static atmosphere model; in the rotating atmospheric model, the orbital inclination  and longitude of the ascending node of the orbit
and longitude of the ascending node of the orbit  are found to decrease, but the variation of
are found to decrease, but the variation of 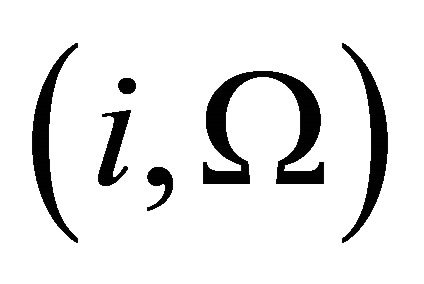 is so small that the orbital plane can be approximated to appear without change.
is so small that the orbital plane can be approximated to appear without change.

Figure 12. Changes of orbital inclination.

Figure 13. Changes of the longitude of the ascending node of the orbit.
The article described the findings of a study evaluating variations in parameters contributing to differences in the longitude of the ascending node and the orbital inclination. The research data show that, when the orbital inclination changes in the range of 0˚ - 9˚ (the longitude of the ascending node of the orbit can be obtained from the formula provided). In the two atmospheric models, orbital parameters (such as the orbital semimajor axis and orbital eccentricity) were found to differ by 4% to 10%.
Case 2: Comparison of time and cost
In this case, a 400 × 400 target track was provided, and some relevant conclusions were obtained through the simulation results. In this model, the orbit inclination was 10˚ and the longitude of the ascending node of the orbit was 60˚. The other initial values are shown in Table 3.
From the simulation results shown in Figure 14, it can be seen that, when the height of the periareon is less than 105 km, the time the Mars vehicle takes to reach the target orbit under the static atmospheric model is less than the time it takes in the rotating atmosphere model. In addition, in the two types of atmospheric models, the biggest difference in the time taken by the Mars vehicle to reach the target orbit is about 6.2 days. Further, if the height of the periareon is more than 105 km, the time taken by the Mars vehicle to reach the target orbit both the atmospheric models will basically be the same.
The atmospheric drag and atmosphere lift are relative to the relative velocity of the Mars vehicle in relation to the atmosphere and atmospheric density. In fact, the

Figure 14. Change of time taken to arrive at the target orbit in different periareon heights.
lower the height of the periareon selected, the greater the atmospheric density becomes. Although the relative velocities of the vehicle in the two atmospheric models are different, the gap between them is very small. In addition, the effect on the orbit of the Mars vehicle is more obvious in the rotating atmospheric model. Therefore, when the periareon is low, the time taken to reach the target orbit in the two atmospheric models is different; however, when the height of the periareon is high, the atmospheric density become smaller. Although the relative velocity value of the Mars vehicle and the atmosphere will increase in the rotating atmospheric model, the difference in the time taken to reach the target orbit in the two atmospheric models is small because the rotational angular velocity of the external rotation atmosphere of Mars is small.
Table 4 shows the increment in the velocity of transfer from actual to target orbit with different periareons of the Mars vehicle in two different atmospheric models. From the contrast shown in the Table 4, it can be seen that, as the height of the periareon increases, the velocity increment consumption of the Mars vehicle in the two atmospheric models shows a trend to increase. In addition, the consumption rate of increment for the detector under the rotating atmospheric model is bigger than that under the static atmospheric model. The biggest difference between these two models is about 10.8%.
4. Conclusions
Transfer trajectory design for Mars exploration is applying combination of invariant manifolds, differential correction and aerobraking method. The whole transfer trajectory is divided into four stages: the part from Earth parking orbit to Lyapunov orbit around Lagrange point L2 in Sun-Earth system, the part from Lyapunov orbits around L2 in Sun-Earth system to L1 in Sun-Mars system, the part from Lyapunov orbit around L1 in Sun-Mars system to the large elliptical orbit around Mars, and the part from the large elliptical orbit around the Mars to near-Mars parking orbit.

Table 4. Cost comparison for transfer under two atmospheric models.
In the first three stages, the circular restricted threebody problem is considered. The four-body problem, Sun-Earth-Mars-vehicle, is decomposed into two coplanar circular restricted three-body problems, Sun-EarthVehicle and Sun-Mars-vehicle. In the first stage, the invariant manifolds of L2 Lyapunov orbit in Sun-Earth system cannot reach the earth parking orbit, so the differential correction method is applied accompany with invariant manifolds. In the second stage, the unstable manifold of L2 Lyapunov orbit in Sun-Earth system will not intersect with stable manifold of L1 Lyapunov orbit in Sun-Mars system, so the transfer trajectory is designed combining the invariant manifold and the differential correction method. To compare with the intermediate transfer trajectory designed by the invariant manifolds of Halo orbit, the results show that using the invariant manifold of Lyapunov orbit has advantages in energy consumption and time of flight, reducing energy consumption 3.78 percent and reducing flight time 23.02 percent in Sun-Earth system, and reducing energy consumption 9.32 percent and reducing flight time 23.02 percent in Sun-Mars system. In the third stage, the invariant manifold of L1 Lyapunov orbit in Sun-Mars system can reach the apareon of the large elliptical orbit around the Mars, so only a maneuver is applied to adjust the velocity of the vehicle, and the differential correction method is not needed.
In the fourth stage, the two-body problem is considered, and the aerobraking method is applied. By comparative analysis of the simulation results of the dynamics equations of the Mars vehicle in the static and rotating atmospheric environments, it can be observed that, in the low periareon, because of higher atmospheric density, the differences in the orbital parameters between the rotating and static atmospheric environments are higher, thus, the time taken by the Mars vehicle to reach the target orbit is different in the two atmospheric models, and the time gap is marked. Moreover, when the periareon in two atmospheric environment models is of the same height, the inclination and longitude of the ascending node of the orbit in the rotating atmospheric environment showed a subtle change, whereas that in the static atmospheric environment remained unchanged.
5. Acknowledgements
This research was supported by the National Natural Science Foundation of China (10832004, 11102006), and the Fan-Zhou Foundation (20110502).
REFERENCES
- J. Barrow-Green, “Poincare and the Three-Body Problem,” American Mathematical Society-London Mathematicl Society, Providence, 1997.
- B. Wie, “Space Vehicle Dynamic and Control,” American Institute of Aeronautics and Astronautics, Reston, 1998.
- R. W. Farquhar, “The Flight of ISEE-3/ICE: Origns, Mission History, and a Legacy,” AAS/AIAA Astrodynamics Specialist Conference and Exhibit, Boston, 10-12 August 1998, pp. 98-4464.
- P. Sharer and T. Harrington, “Trajectory Optimization for the ACE Halo Orbit Mission,” AAS/AIAA Astrodynamics Specialist Conference, San Diego, 29-31 July 1996, pp. 96-3601.
- P. Sharer and D. Folta, “Wind Extended Mission Design,” AAS/AIAA Astrodynamics Conference, San Diego, 29-31 July 1996, pp. 96-3640.
- H. Franz, P. Sharer, K. Ogilvie and M. Desch, “Wind Nominal Mission Performance and Extended Mission Design,” AAS/AIAA Astrodynamics Specialist Conference and Exhibit, Boston, 10-12 August 1998, pp. 98- 4467.
- O. O. Cuevs, L. Kraft-Newman, M. A. Mesarch and M. Woodard, “An Overview,” AAS/AIAA Astrodynamics Specialist Conference and Exhibit, Monterey, 5-8 August 2002, pp. 2002-4425.
- M. A. Mesarch, D. Rohrbaugh and C. Schiff, “Contingency Planning for the Microwave Anisotropy Probe Mission,” AAS/AIAA Astrodynamics Specialist Conference and Exhibit, Monterey, 5-8 August 2002, pp. 2002- 4426.
- S. Stalos, D. Folta, B. Short, J. Jen and A. Seacord, “Optimum Transfer to Largeamplitude Halo Orbit for the Solar and Heliospheric Observatory,” AAS/GSFC International Symposium on Space Flight Dynamics, Greenbelt, 26-30 April 1993, pp. 93-553.
- W. S. Koon, M. W. Lo, J. E. Marsden and S. D. Ross, “Dynamical Systems, the Three-Body Problem, and Space Mission Design,” Springer, Berlin, 2007.
- M. W. Lo, “The Interplanetary Superhighway and the Origins Program,” IEEE Aerospace 2002 Conference, Big Sky, 9-16 March 2002, pp. 3543-3562.
- W. S. Koon, W. Martin, M. W. Lo, J. E. Marsden and S. D. Ross, “Shoot the Moon,” AAS/AIAA Astrodynamics Specialist Conference, Clearwater, 2000, pp. 100-167.
- W. S. Koon, M. W. Lo, J. E. Marsden and S. D. Ross, “Low Energy Transfer to the Moon,” Celestial Mechanics and Dynamical Astronomy, Vol. 81, No. 1-2, 2001, pp. 63-73. doi:10.1023/A:1013359120468
- G. Gomez, W. S. Koon, M. W. Lo, J. E. Marsden and J. J. Masdemont, “Connecting Orbits and Invariant Manifold in the Spatial Restricted Three-Body Problem,” Nonlinearity, Vol. 17, No. 5, 2004, pp. 1571-1606. doi:10.1088/0951-7715/17/5/002
- K. C. Howell, D. L. Mains and B. T. Barden, “Transfer Trajectories from Earth Parking Orbits to Sun-Earth Halo Orbits,” AAS/AIAA Spaceflight Mechanics Meeting, Cocoa Beach, 14-16 February 1994, pp. 94-160.
- E. A. Belbruno and J. K. Miller, “Sun-Peturbed Earth-toMoon Transfers with Ballistic Capture,” Journal of Guidance, Control, and Dynamics, Vol. 16, No. 4, 1993, pp. 770-775. doi:10.2514/3.21079
- G. P. Alonso, “The Design of System-to-System Transfer Arcs Using Invariant Manifolds in the Multi-Body Problem,” Ph.D. Dissertation, Purdue University, West Lafayette, 2006.
- F. Topputo, M. Vasile and A. E. Finzi, “Combining Two and Three-Body Dynamics for Low Energy Transfer Trajectories of Practical Interest,” Proceedings of the 55th International Astronautical Congress, Vancouver, 4-8 October 2004, pp. 584-596.
- M. Xu and S. J. Xu, “Stability Analysis and Transiting Trajectory Design for Retrograde Orbits around Moon,” Journal of Astronautics, Vol. 30, No. 5, 2009, pp. 1785- 1791.
- M. J. Capinski, “Lyapunov Orbits at L2 and Transversal Intersections of Invariant Manifolds in the Jupiter-Sun Planar Restricted Circular Three-Body Problem,” 2011. http://arxiv.org/pdf/1109.1439v2.pdf
- J. Llibre, J. R. Martlnez and C. Simo, “Transversality of the Invariant Manifolds Associated to the Lyapunov Family of Periodic Orbits near L2 in the Restricted ThreeBody Problem,” Journal of Differential Equations, Vol. 58, No. 1, 1985, pp. 104-156. doi:10.1016/0022-0396(85)90024-5
- H. X. Baoyin and C. R. McInnes, “Trajectories to and from the Lagrange Points and the Primary Body Surfaces,” Journal of Guidance, Control and Dynamics, Vol. 29, No. 4, 2006, pp. 998-1003. doi:10.2514/1.17757
- S. P. Gong, J. F. Li and H. X. Baoyin, “Lunar Landing Trajectory Design Based on Invariant Manifold,” Applied Mathematics and Mechanics, Vol. 28, No. 2, 2007, pp. 201-207. doi:10.1007/s10483-007-0208-1
- X. Min, T. Pan and H. Guo, “Analysis of Orbit Capture Method for Mars Vehicle,” Spacecraft Engineering, Vol. 17, No. 6, 2008, pp. 39-43.
- F. Xiao, “Man-Made Earth Satellite Orbit Perturbation Theory,” Press of National University of Defense Technology, Changsha, 1995, pp. 178-192.
- Kh. I. Khalil, “The Drag Exerted by an Oblate Rotating Atmosphere on an Artifical Satellite,” Applied Mathematics and Mechanics, Vol. 23, No. 9, 2002, pp. 903-915. doi:10.1007/BF02437712
- D. L. Richardson, “Periodic Orbits about the L1 and L2 Collinear Points in the Circular-Restricted Problem,” Computer Sciences Corporation, Technical Report, 1978.
- K. C. Howell, B. T. Barden and M. W. Lo, “Application of Dynamical Systems Theory to Trajectory Design for a Lagrange Point Mission,” Journal of Astronautical Sciences, Vol. 45, No. 1, 1997, pp. 161-178.
- K. C. Howell, B. T. Barden, R. S. Wilson, et al., “Trajectory Design Using a Dynamical Systems Approach with Application to Genesis,” AAS/AIAA Astrodynamics Specialist Conference, Sun Valley, 4-7 August 1997, pp. 68-178.

