International Journal of Astronomy and Astrophysics
Vol.3 No.1(2013), Article ID:29417,12 pages DOI:10.4236/ijaa.2013.31002
Riemannian Space-Time, de Donder Conditions and Gravitational Field in Flat Space-Time
Copernicus Institute for Physics and Astronomy, Toronto, Canada
Email: gordonliu168@gmail.com
Received December 1, 2012; revised January 3, 2013; accepted January 12, 2013
Keywords: General Relativity; Gravitation; Riemannian Space-Time; Flat Space-Time; Einstein Equations; Harmonic Conditions; Energy-Momentum Tensor; Significance of the Coordinates; Gravitational Red-Shift
ABSTRACT
Let the coordinate system of flat space-time to absorb a second rank tensor field
of flat space-time to absorb a second rank tensor field  of the flat space-time deforming into a Riemannian space-time, namely, the tensor field
of the flat space-time deforming into a Riemannian space-time, namely, the tensor field 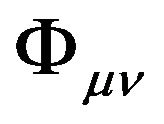 is regarded as a metric tensor with respect to the coordinate system
is regarded as a metric tensor with respect to the coordinate system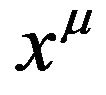 . After done this,
. After done this, 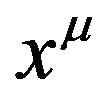 is not the coordinate system of flat space-time anymore, but is the coordinate system of the new Riemannian space-time. The inverse operation also can be done. According to these notions, the concepts of the absorption operation and the desorption operation are proposed. These notions are actually compatible with Einstein’s equivalence principle. By using these concepts, the relationships of the Riemannian space-time, the de Donder conditions and the gravitational field in flat space-time are analyzed and elaborated. The essential significance of the de Donder conditions (the harmonic conditions or gauge) is to desorb the tensor field of gravitation from the Riemannian space-time to the Minkowski space-time with the Cartesian coordinates. Einstein equations with de Donder conditions can be solved in flat space-time. Base on Fock’s works, the equations of gravitational field in flat space-time are obtained, and the tensor expression of the energy-momentum of gravitational field is found. They all satisfy the global Lorentz covariance.
is not the coordinate system of flat space-time anymore, but is the coordinate system of the new Riemannian space-time. The inverse operation also can be done. According to these notions, the concepts of the absorption operation and the desorption operation are proposed. These notions are actually compatible with Einstein’s equivalence principle. By using these concepts, the relationships of the Riemannian space-time, the de Donder conditions and the gravitational field in flat space-time are analyzed and elaborated. The essential significance of the de Donder conditions (the harmonic conditions or gauge) is to desorb the tensor field of gravitation from the Riemannian space-time to the Minkowski space-time with the Cartesian coordinates. Einstein equations with de Donder conditions can be solved in flat space-time. Base on Fock’s works, the equations of gravitational field in flat space-time are obtained, and the tensor expression of the energy-momentum of gravitational field is found. They all satisfy the global Lorentz covariance.
1. Introduction
Although General Relativity (GR) is widely accepted wherewith its graceful structures and elegance of its concepts, also giving a description of gravitational phenomena in agreement with observation, it is rather disconcerting to note that the theory appears strikingly different from the present particle theory. Gravitation plays a unique role in physics, as it is connected with the geometry of space and time. Supersymmetry appears to be required to have a perturbative quantum theory that includes gravitons and is also exactly Lorentz invariant. Whether the observed global Lorentz invariance of flat space-time is realized exactly in nature [1]? The notions of energy and momentum play an important role in physics, while there is no widely accepted way to localize the energy and momentum of the gravitational field itself [2].
Facing those disharmonies, a number of authors have discussed the utility of introducing the metric of flat background space-time into GR [3-22]. Those theories called the bi-metric gravitation or the field-theoretical approach to General Relativity. All of authors have been aware of that there is a correct intrinsic structure in GR, even if they feel uncomfortable with purely geometrical interpretation of gravitation. That is the structural form of Einstein equations! That is why all of authors guess their Lagrangian densities according to the Einstein equations in order to corresponding with Einstein equations. However, in those theories, some authors assume that two metric tensors, the Riemannian space-time and flat background space-time, exist at the same time; while others assigned have no particular fundamental or geometric significance to the relationships of the Riemannian space-time, the gravitational field and the flat back-ground space-time [2,23]. Some questions naturally arise. Why is the structural form of Einstein equations correct even if it is obtained from the geometric interpretation that people feel uncomfortable? What relationship between the gravitational field and the Riemannian space-time is exactly? Can we find a way to hold the structural form of Einstein equations, abandon the purely geometric interpretation of gravitation and make the equations global Lorentz invariance? Or can we regard Einstein equations as the equations of gravitation in flat space-time?
The present paper is intended to answer above questions. To do this, for the convenience to express the concepts of the absorption and desorption, the motion equations of a freely falling particle in a gravitational field will be derived in chapter 2. Then, in chapter 3, the concepts of the absorption and desorption will be introduced to find the relationship between the Riemannian spacetime and the tensor field in the flat space-time. The equations of gravitational field and the expression of the energy-momentum tensor of gravitational field in the flat space-time will be obtained in chapter 4. Furthermore, the significance of the coordinates and the essence of the gravitational red-shift will be analyzed and elaborated.
2. Kinematics of a Freely Falling Particle in Gravitational Field
2.1. Approximate Analysis of Newton’s Theory of Gravitation in the Minkowski Space-time
In the inertial reference frames with Cartesian coordinate system  (English letters i, j, etc. take 0, 1, 2, 3, denote that the physical quantities are in the Minkowski spacetime with Cartesian coordinates
(English letters i, j, etc. take 0, 1, 2, 3, denote that the physical quantities are in the Minkowski spacetime with Cartesian coordinates ), the metric tensor is
), the metric tensor is . The freely falling particle moves in the Newton gravitational field. Considering approximation,
. The freely falling particle moves in the Newton gravitational field. Considering approximation,  (c is light speed in vacuum), its Lagrangian density is
(c is light speed in vacuum), its Lagrangian density is
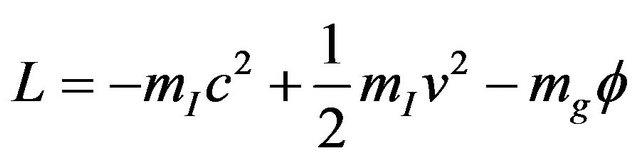 . (1)
. (1)
Here 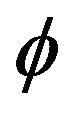 is the Newton potential and
is the Newton potential and 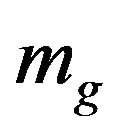 is the gravitational mass of a freely falling particle. Assuming
is the gravitational mass of a freely falling particle. Assuming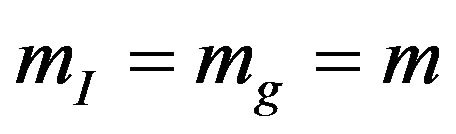 , in other words, the inertial mass is equal to the gravitational mass. This is the weak equivalence principle (WEP) [24]. Eotvos, Dicke, etc. have precisely proven this conclusion by using their examination [25]. Thereout, we arrive at the classical approximate action of the particle in the Newton gravitational field,
, in other words, the inertial mass is equal to the gravitational mass. This is the weak equivalence principle (WEP) [24]. Eotvos, Dicke, etc. have precisely proven this conclusion by using their examination [25]. Thereout, we arrive at the classical approximate action of the particle in the Newton gravitational field,
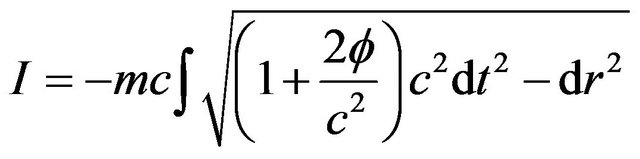 , (2)
, (2)
where . Write the formula (2) as
. Write the formula (2) as
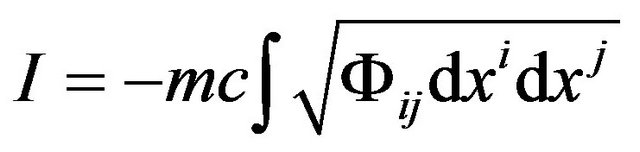 , (3)
, (3)
where
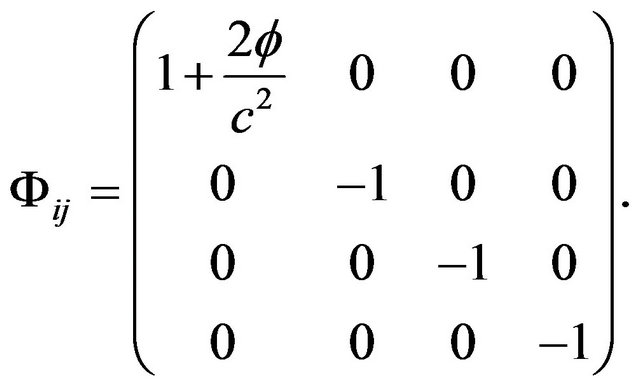 (4)
(4)
We can see that the tensor  is obviously related to the gravitational potential (GP) and the metric tensor of the Minkowski space-time. We call this the General Gravitational Potential (GGP) tensor.
is obviously related to the gravitational potential (GP) and the metric tensor of the Minkowski space-time. We call this the General Gravitational Potential (GGP) tensor.
2.2. The Motion Equations of a Freely Falling Particle in Gravitational Field
Via the formulas (3) and (4), we are inspired to extend them to precise forms in the Minkowski space-time. We take
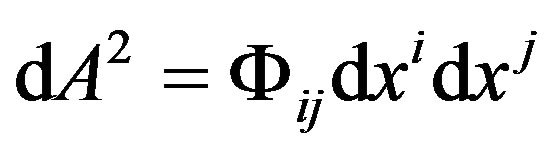 . (5)
. (5)
Here 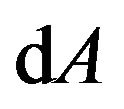 is a scalar which is constituted by the GGP tensor
is a scalar which is constituted by the GGP tensor 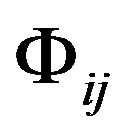 and
and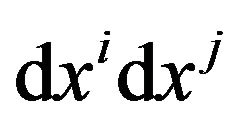 , called Gravitational Action (GA) line element.
, called Gravitational Action (GA) line element.  Hence, the action of a particle in gravitational field
Hence, the action of a particle in gravitational field
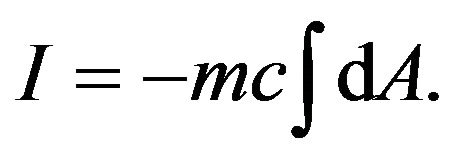 (6)
(6)
Via 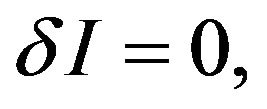 we deduce the motion equations of a freely falling particle in gravitational field in an inertial reference frame,
we deduce the motion equations of a freely falling particle in gravitational field in an inertial reference frame,
 . (7)
. (7)
We easily obtain
 (8)
(8)
where
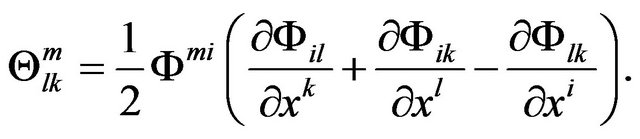 (9)
(9)
Note that 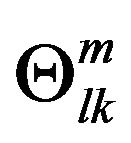 is not the affine connection, and also
is not the affine connection, and also  is not the line element of space-time, call
is not the line element of space-time, call 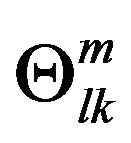 the General Strength (GS) of gravitational field. The spacetime is still the Minkowski space-time, and the reference frame is the inertial reference frame. This is completely no relationship with Riemann geometry.
the General Strength (GS) of gravitational field. The spacetime is still the Minkowski space-time, and the reference frame is the inertial reference frame. This is completely no relationship with Riemann geometry.
2.3. The General Motion Equations of a Freely Falling Particle
To extend the motion Equations (8) and (9) to a noninertial reference frame with the coordinates 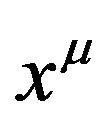 (The Greek letters
(The Greek letters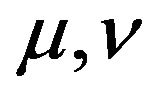 , etc. take 0, 1, 2, 3 and denote the curved coordinates in the non-inertial reference frames or in the Riemannian space-time. Its metric tensor is
, etc. take 0, 1, 2, 3 and denote the curved coordinates in the non-inertial reference frames or in the Riemannian space-time. Its metric tensor is ), we obtain the general motion equations. Due to the equations satisfying the covariance under the coordinate transformation between arbitrary real reference frames, they are same in form,
), we obtain the general motion equations. Due to the equations satisfying the covariance under the coordinate transformation between arbitrary real reference frames, they are same in form,
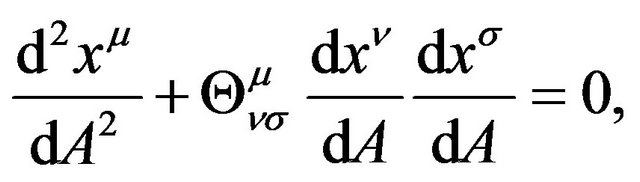 (10)
(10)
where
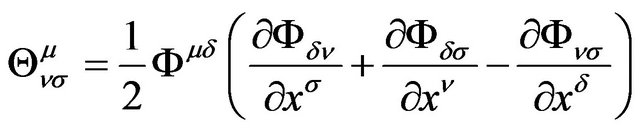 . (11)
. (11)
Note that, here 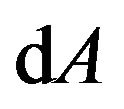 is not the line element of spacetime, but is the GA line element;
is not the line element of spacetime, but is the GA line element; 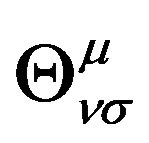 is not the affine connection of space-time, but is the general strength of gravitation.
is not the affine connection of space-time, but is the general strength of gravitation.
3. A-D Operation and Deformation of Space-Time
3.1. Absorption Operation (A)
We construct a scalar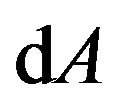 by using a tensor field
by using a tensor field 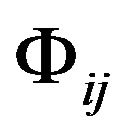 and the vectors
and the vectors 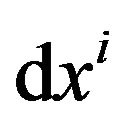 and
and  in a flat space-time,
in a flat space-time,
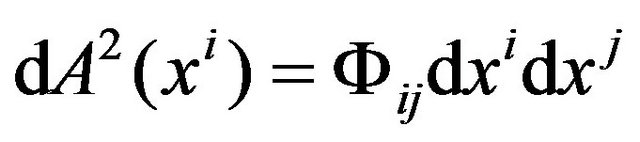 . (12)
. (12)
Here 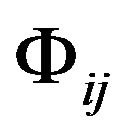 is not the metric tensor of the coordinate system
is not the metric tensor of the coordinate system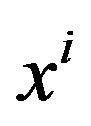 . The formula (12) is same as the GA line element (5). Let
. The formula (12) is same as the GA line element (5). Let  absorb
absorb , namely,
, namely, 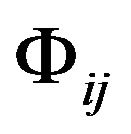 is regarded as the metric tensor of the coordinate system
is regarded as the metric tensor of the coordinate system . Thus, the coordinates
. Thus, the coordinates 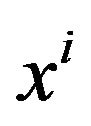 in the flat space-time become the curved coordinates
in the flat space-time become the curved coordinates  in a Riemannian space-time; the tensor field
in a Riemannian space-time; the tensor field  in the flat space-time becomes the metric tensor
in the flat space-time becomes the metric tensor 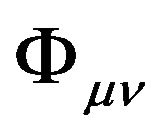 in the Riemannian space-time. We have
in the Riemannian space-time. We have
 . (13)
. (13)
According to the convention of General Relativity, it can be written as
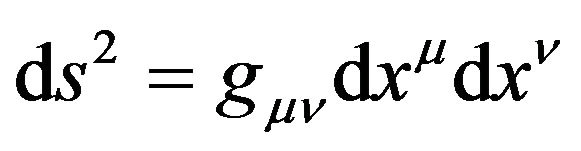 . (14)
. (14)
Here we respectively replace 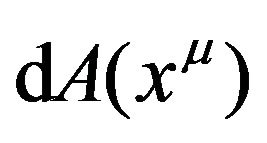 and
and 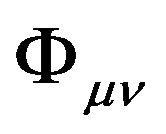 by ds and
by ds and . In this way, the original flat space-time and the tensor field are together deformed into a new Riemannian space-time. We must emphasize that this deformation is global or whole space-time, but it is not a mapping in a traditional mathematical sense. We call this operation as the absorption operation. We will use
. In this way, the original flat space-time and the tensor field are together deformed into a new Riemannian space-time. We must emphasize that this deformation is global or whole space-time, but it is not a mapping in a traditional mathematical sense. We call this operation as the absorption operation. We will use  to denote the absorption operation.
to denote the absorption operation.
To help us understanding this deformation, we have a similar visualized example. Dropping a drop of water on a dry plane paper, the paper will absorb the water and form an embossment. The plane paper is a flat space; the water is similar to the second rank tensor field; the surface of the wet embossment looks like the 2D Riemannian space. Another similar example for understanding the concept of the absorption is that Schwarzschild had done when he solved Einstein equation. He assumed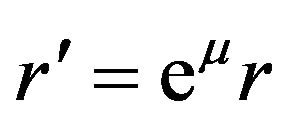 . The factor
. The factor 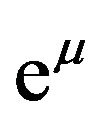 was absorbed into
was absorbed into .
.
The formula (12) and (14) are completely identical with regard to the form and the structure, but they give different meanings. We do not even need to change the symbols. The only reason we replace above symbols is to avoid confusion about its meanings. When  and
and 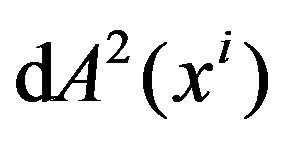 are respectively regarded as the metric tensor and the metric (line element) of the Riemannian spacetime, the coordinate system
are respectively regarded as the metric tensor and the metric (line element) of the Riemannian spacetime, the coordinate system  actually becomes the coordinate system of the new Riemannian space-time and is not the coordinate system of the flat space-time anymore. Normally this change is not been aware of by us [3-22,26], because the formulas are not changed and keep the same in form, but their meanings are totally changed.
actually becomes the coordinate system of the new Riemannian space-time and is not the coordinate system of the flat space-time anymore. Normally this change is not been aware of by us [3-22,26], because the formulas are not changed and keep the same in form, but their meanings are totally changed.
From the absorption operation we can see, in form, the Minkowski space-time 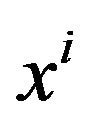 with a second rank tensor field
with a second rank tensor field  which is only the function of the space-time is equivalent to the Riemannian space-time
which is only the function of the space-time is equivalent to the Riemannian space-time 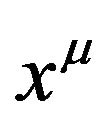 with the metric tensor
with the metric tensor . This is the geometric theory of gravitation that Einstein arrived at by using the equivalence principle and by regarding the gravitation field in the Minkowski space-time as a Riemannian space-time. The logical essence of General Relativity is to let the coordinates of flat space-time absorb the second rank tensor field of gravitation and form a Riemannian spacetime, thereby realizing geometrization of gravitation.
. This is the geometric theory of gravitation that Einstein arrived at by using the equivalence principle and by regarding the gravitation field in the Minkowski space-time as a Riemannian space-time. The logical essence of General Relativity is to let the coordinates of flat space-time absorb the second rank tensor field of gravitation and form a Riemannian spacetime, thereby realizing geometrization of gravitation.
After taking the absorption operation, the space-time is deformed, on which the structural forms of the scalar dA, vector  and tensor
and tensor  remain the same.
remain the same.
We can use a mathematical way to express the absorption operation 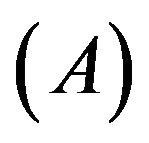 which is
which is
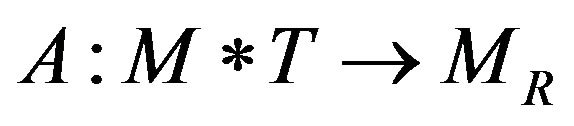 , (15)
, (15)
A denotes the absorption operation; 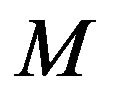 denotes the original space-time;
denotes the original space-time; 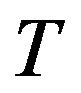 denotes a second rank tensor field in the original space-time;
denotes a second rank tensor field in the original space-time; 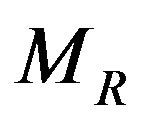 denotes the new Riemannian space-time;
denotes the new Riemannian space-time; 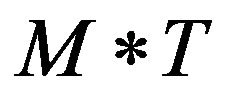 denotes the coupling of the space-time and the tensor field.
denotes the coupling of the space-time and the tensor field.
3.2. Desorption Operation (D)
In opposition to the absorption operation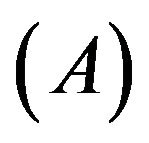 , a Riemannian space-time can be deformed to a new flat background space-time with a second rank tensor field. This second rank tensor field is the metric tensor desorbed from the original Riemannian space-time. Both tensors are identical in form and structure. We call this operation as the desorption operation
, a Riemannian space-time can be deformed to a new flat background space-time with a second rank tensor field. This second rank tensor field is the metric tensor desorbed from the original Riemannian space-time. Both tensors are identical in form and structure. We call this operation as the desorption operation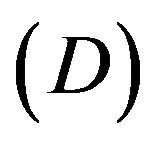 . The selection of the background space-time is important. In physics, we ought to choose the background space-time that has real physical meaning. This relates to the selection of reference frame and coordinate system. Later we will see that Einstein and all the authors who use the de Donder conditions and the asymptotically flat condition is actually to desorb the gravitation field (metric tensor field) from the coordinate system of the Riemannian space-time, moreover, to choose the inertial reference frame and the Cartesian coordinate system.
. The selection of the background space-time is important. In physics, we ought to choose the background space-time that has real physical meaning. This relates to the selection of reference frame and coordinate system. Later we will see that Einstein and all the authors who use the de Donder conditions and the asymptotically flat condition is actually to desorb the gravitation field (metric tensor field) from the coordinate system of the Riemannian space-time, moreover, to choose the inertial reference frame and the Cartesian coordinate system.
We can use mathematical way to express the desorption operation  which is
which is
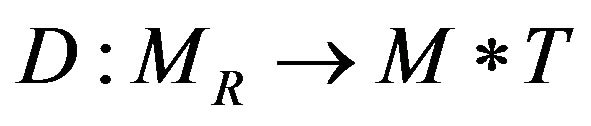 . (16)
. (16)
3.3. The Equivalence Principle and the A-D Operation Because the gravitational mass is equal to the inertial mass, in Dynamics, an accelerated local reference frame is equivalent to a local gravitation field. Which is to say, a gravitational field is equivalent to an united entity of the infinite amount of infinitesimal accelerated local reference frames. Therefore, we consider that a gravitational field is equivalent to a curved Riemannian spacetime. This is logical essence of the equivalence principle. We have mentioned above, this way is equivalent to the absorption operation. It is equal to let the coordinates to absorb the GGP tensor and the GGP tensor become the metric tensor of a new coordinate system, thereby, to form a Riemannian space-time.
The other way round, a tangent space of the Riemannian space-time can be regarded as an accelerated freely falling local frame which takes the geodesic as the coordinate system frame. These local frames are the accelerated infinitesimal local frames relative to an inertial reference frame. Although their GA line elements are identical in form with the line element of the space-time in the inertial reference frame when there is no gravitation field, they still possess the intrinsic characteristic of the Riemannian space-time. In other words, the intrinsic characteristic of the gravitational field, such as their curvature tensor is non-zero. These accelerated infinitesimal local frames exist one to one corresponding coordinate transformation relationships with the space-time of the inertial reference frame. The coordinate transformation relationships are not only one, but infinite. Each local frame has one transformation relationship with the inertial reference frame, because every local frame has different acceleration relative to the inertial reference frame. Here we cannot find a globally mapping in a traditional mathematical sense. However, all of scalars and tensors in the local frame can be transferred to the inertial reference frame through the coordinate transformation. The scalars and tensors remain identical in form, owing to that the scalars and tensors are covariant with respect to arbitrary coordinate transformation.
The line element of the tangent space of the Riemannian space-time, namely the GA line element in the accelerated freely falling local frame, is the resultant effect of the deformation of the background space-time  and the GGP tensor
and the GGP tensor  in the local frame. In an arbitrary accelerated frame, the line element of the background space-time is
in the local frame. In an arbitrary accelerated frame, the line element of the background space-time is
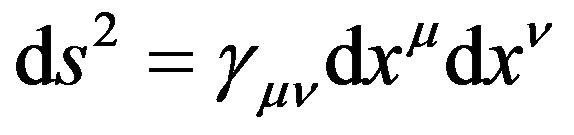 , (17)
, (17)
the GGP tensor is 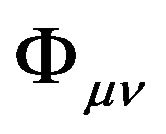 and their GA line element is
and their GA line element is
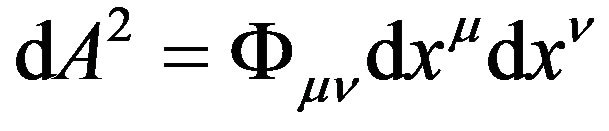 . (18)
. (18)
If choosing the accelerated freely falling local frame moving along with the geodetic and the Cartesian coordinates, we have
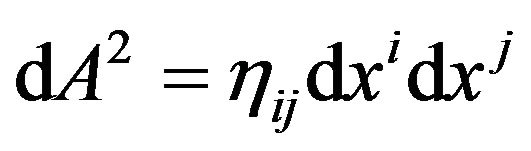 . (19)
. (19)
In this special case, the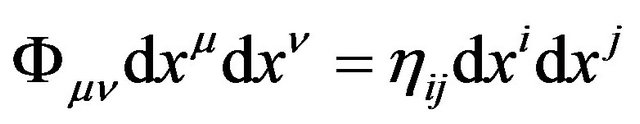 . This is completely identical in form with the line element of the Minkowski space-time
. This is completely identical in form with the line element of the Minkowski space-time
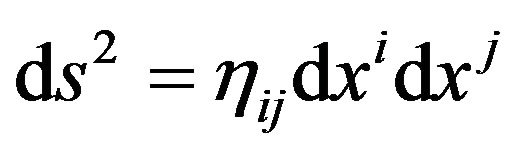 . (20)
. (20)
This is the reason that one believe that the freely falling local frames are local inertial frame.
When we transfer the coordinates between all accelerated freely falling local frames and an inertial reference frame, the line element (metric) of the background space-time (17) becomes (20), and the GA line element (19) remains covariant, namely
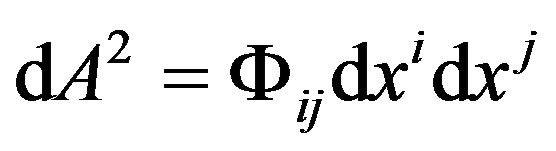 . (21)
. (21)
Note, this is different from the formula (18), thereinto, 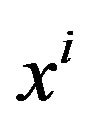 is the coordinate system of the inertial frame and not of the accelerated frame. We have noted that in form the
is the coordinate system of the inertial frame and not of the accelerated frame. We have noted that in form the  in the formula (21) actually is the metric
in the formula (21) actually is the metric  of the Riemannian space-time.
of the Riemannian space-time.
From the formula (21) we know that the GGP tensor field  can be desorbed from the Riemannian spacetime. In other words, the metric tensor in a Riemannian space-time can be desorbed to a background space-time and becomes to a tensor field. This is the desorption operation
can be desorbed from the Riemannian spacetime. In other words, the metric tensor in a Riemannian space-time can be desorbed to a background space-time and becomes to a tensor field. This is the desorption operation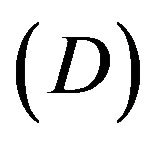 .
.
3.4. Tensor Remains Invariant in Form under A-D Operation
The space-time can be deformed by taking the absorption operation  and the desorption operation
and the desorption operation . How will the tensors in the space-time vary after the spacetime is deformed under the two operations A-D?
. How will the tensors in the space-time vary after the spacetime is deformed under the two operations A-D?
According to the Equivalence Principle, we know that the tensors in the flat space-time remain identical in form with in the Riemannian space-time. The other way round is also true. The metric tensor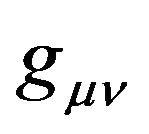 and the line element (metric)
and the line element (metric)  in the Riemannian space-time respectively become the second rank tensor field
in the Riemannian space-time respectively become the second rank tensor field 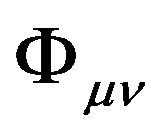 and the GA line element
and the GA line element 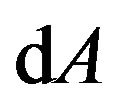 in the flat space-time. By the same token, all the tensors in the Riemannian space-time have the same form as in the flat space-time. That is to say, tensors remain invariant in form under deformation of the space-time. Therefore, tensors in form remain invariant under the A-D operation.
in the flat space-time. By the same token, all the tensors in the Riemannian space-time have the same form as in the flat space-time. That is to say, tensors remain invariant in form under deformation of the space-time. Therefore, tensors in form remain invariant under the A-D operation.
4. The Equations of Gravitation Field
In chapter 2, we have found the general equations of motion of a particle in a gravitational field (10) and (11), but we do not know the exact forms of the GGP tensor and thus cannot solve the equations of motion. How to find the GGP tensor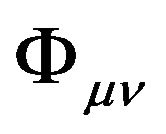 ? First of all, we have to find the equations in respect to
? First of all, we have to find the equations in respect to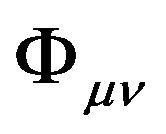 , namely the equations of the gravitational field. These are the questions we will be discussing in this chapter.
, namely the equations of the gravitational field. These are the questions we will be discussing in this chapter.
4.1. The Tensor That Embodies the Existence of Gravitation Field
First of all, we investigate the gravitation field by taking Cartesian coordinates in an inertial reference frame. In the formula (5), the GGP tensor 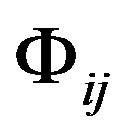 is a second rank tensor field of the Minkowski space-time which is relative to the gravitational field and is only the function of space-time. When the gravitational field vanishes,
is a second rank tensor field of the Minkowski space-time which is relative to the gravitational field and is only the function of space-time. When the gravitational field vanishes, 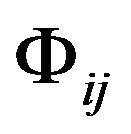 becomes the metric tensor
becomes the metric tensor 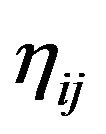 of the Minkowski spacetime. While the gravitational field exists, regardless of which reference frame is chosen and what coordinates are used, we cannot transform
of the Minkowski spacetime. While the gravitational field exists, regardless of which reference frame is chosen and what coordinates are used, we cannot transform 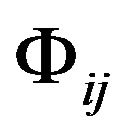 to the metric tensor
to the metric tensor  in the whole space-time. Namely, we cannot eliminate the gravitational effect in the whole of the space-time by choosing reference frames and coordinates. In principle, we can make certain
in the whole space-time. Namely, we cannot eliminate the gravitational effect in the whole of the space-time by choosing reference frames and coordinates. In principle, we can make certain 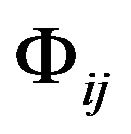 and its equations through a large variety of experiments, like Electromagnetism, but we do not have enough experimental results to summarize those equations. Nevertheless, we can find the intrinsic structural properties of a gravitational field from Riemann geometry, namely find out the geometric quantities which embody the intrinsic properties of the Riemannian space-time and desorb them to the flat spacetime. Those geometric quantities desorbed are the quantities which embody the intrinsic structural properties of the gravitational field.
and its equations through a large variety of experiments, like Electromagnetism, but we do not have enough experimental results to summarize those equations. Nevertheless, we can find the intrinsic structural properties of a gravitational field from Riemann geometry, namely find out the geometric quantities which embody the intrinsic properties of the Riemannian space-time and desorb them to the flat spacetime. Those geometric quantities desorbed are the quantities which embody the intrinsic structural properties of the gravitational field.
According to the notion of the deformation of spacetime, we practice the absorption operation (A) to the formula (5),
 . (22)
. (22)
In this way,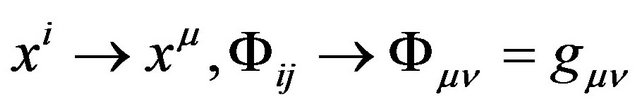 . We gain a Riemannian space-time
. We gain a Riemannian space-time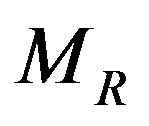 , which has the line element
, which has the line element
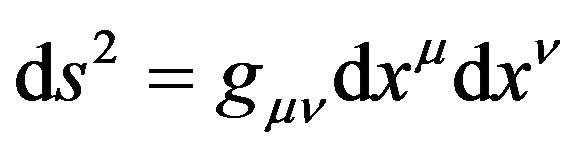 . (23)
. (23)
In Riemann geometry, the essential quantity which can truly embody the curved characteristic of space is the curvature tensor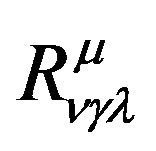 . The tensor
. The tensor  is constructed by the first rank and second rank differentiation of
is constructed by the first rank and second rank differentiation of . In my point of view, this curvature tensor is the essential quantity which embodies the existence of the gravitational field in the space. If the curvature tensor vanishes, the formula (23) can be transformed to the metric of the Minkowski space-time and the gravitational effect can be eliminated in the whole of the space by choosing the reference frame and the coordinates. Therefore, the curvature tensor is the only quantity which embodies the existence of a gravitational field. Einstein tensor can be constructed by the curvature tensor,
. In my point of view, this curvature tensor is the essential quantity which embodies the existence of the gravitational field in the space. If the curvature tensor vanishes, the formula (23) can be transformed to the metric of the Minkowski space-time and the gravitational effect can be eliminated in the whole of the space by choosing the reference frame and the coordinates. Therefore, the curvature tensor is the only quantity which embodies the existence of a gravitational field. Einstein tensor can be constructed by the curvature tensor,
 (24)
(24)
and
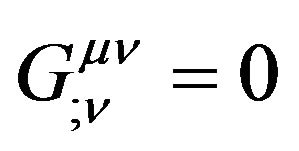 . (25)
. (25)
Here semicolon “;” denotes the covariant derivatives with respect to the Riemannian metric. Because the tensors in form remain invariant under the A-D operation, we can obtain the tensor in the Minkowski space-time,
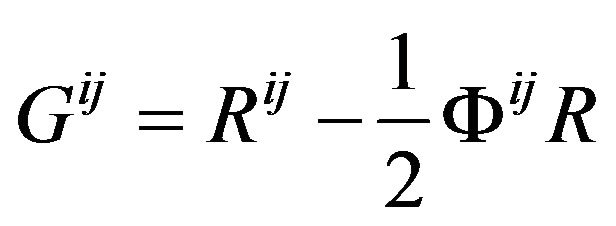 . (26)
. (26)
Here we use Cartesian coordinates.
4.2. The Source of Gravitation Field
The source of gravitation field in Newton theory is the gravitational mass. We can reason and conclude that the energy-momentum tensor of matter is the source of gravitational field.
Because the gravitational mass is equal to the inertial mass (WEP), and the inertial mass  is equal to the rest energy of matter
is equal to the rest energy of matter  divided by the square of light speed
divided by the square of light speed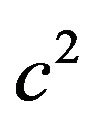 , if we take the units of c = 1, we can clearly see
, if we take the units of c = 1, we can clearly see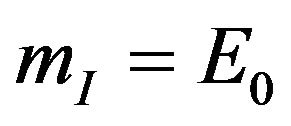 . The inertial mass is just the rest energy of matter. Therefore, the essence of the gravitational mass is the rest energy of matter. The gravitational mass and the inertial mass are the different manifestations of the rest energy of matter. They are actually one physical quantity. The energy of matter is the component of the energy-momentum tensor of matter. The more general expression ought to be the energy-momentum tensor. The source of gravitational field is the energy-momentum tensor of matter.
. The inertial mass is just the rest energy of matter. Therefore, the essence of the gravitational mass is the rest energy of matter. The gravitational mass and the inertial mass are the different manifestations of the rest energy of matter. They are actually one physical quantity. The energy of matter is the component of the energy-momentum tensor of matter. The more general expression ought to be the energy-momentum tensor. The source of gravitational field is the energy-momentum tensor of matter.
We can deduce that the energy-momentum tensor of matter is the source of its gravitation field according to WEP. The other way round, if supposing the source of gravitation field is the energy-momentum tensor of matter, we can reason and arrive at that the gravitational mass is essentially the inertial mass, and both are the different manifestations of the rest energy of matter in different circumstances.
4.3. The Relation of the General Gravitation Potential Tensor and the Energy-Momentum Tensor
Consider Newton’s approximation and Poisson’s equation
 . (27)
. (27)
The right-hand side of the accurate equation of the field we are exploring should be the energy-momentum tensor of matter, because the general expression of the source of gravitational field is the energy-momentum tensor , and the tensor
, and the tensor  becomes to the mass density
becomes to the mass density 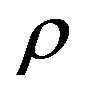 in Newtonian approximation. In this way, the left-hand side of the equation will be a tensor which involves linearly the second order derivatives of the GGP tensor
in Newtonian approximation. In this way, the left-hand side of the equation will be a tensor which involves linearly the second order derivatives of the GGP tensor . We can expect that the Newtonian theory of gravitation can be an approximation of these kinds of tensor equations.
. We can expect that the Newtonian theory of gravitation can be an approximation of these kinds of tensor equations.
In Riemann geometry, the tensors which embody its intrinsic properties, involves linearly the second order derivatives and builds up from 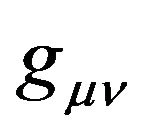 and its first and second order derivatives is only Riemannian-Christoffel tensor
and its first and second order derivatives is only Riemannian-Christoffel tensor 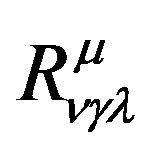 and its contraction, moreover
and its contraction, moreover 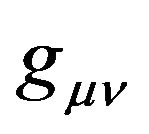 itself. Here appears again the curvature tensor
itself. Here appears again the curvature tensor . Previously, we have already pointed out that this quantity embodies the existence of a gravitational field. By considering the factors above, after desorbing to a Minkowski space-time, the most general form of the left-hand side of the equations can only be
. Previously, we have already pointed out that this quantity embodies the existence of a gravitational field. By considering the factors above, after desorbing to a Minkowski space-time, the most general form of the left-hand side of the equations can only be
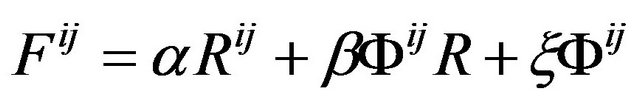 . (28)
. (28)
Here α, β, and ξ are arbitrary constant. Hence the most general form of the equations are
 . (29)
. (29)
Here 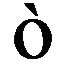 is constant. The tensor
is constant. The tensor  is the energymomentum tensor of all matter in the gravitational field which includes the coupling of matter and gravitation, other than the energy-momentum of gravitational field.
is the energymomentum tensor of all matter in the gravitational field which includes the coupling of matter and gravitation, other than the energy-momentum of gravitational field.
Considering the formula (25) and the conservation law of energy-momentum in the Riemannian space-time,
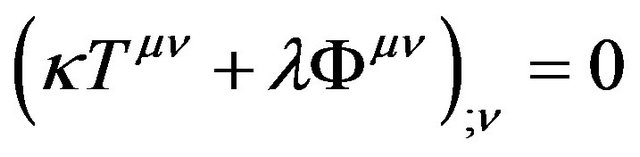 . (30)
. (30)
We ought to adopt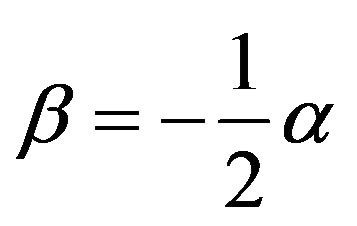 , namely combine
, namely combine 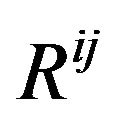
and 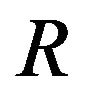 into
into 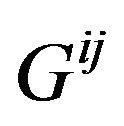 and thus arrive at the equations
and thus arrive at the equations
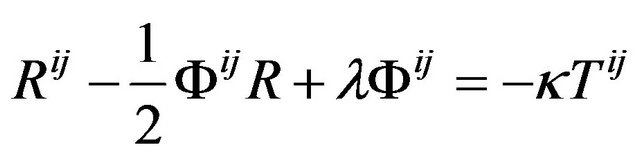 . (31)
. (31)
Here 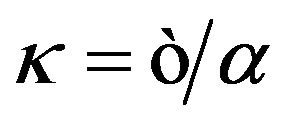 and
and 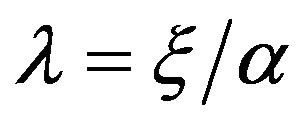 is the cosmological constant. The term
is the cosmological constant. The term 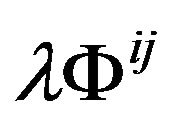 denotes the energy-momentum of cosmological vacuum in the gravitational field which includes the coupling of vacuum and gravitation. This is identical in form with Einstein equations, but it is only in form. We have noticed that the Equations (31) has different meaning with Einstein equations. In the Equation (31),
denotes the energy-momentum of cosmological vacuum in the gravitational field which includes the coupling of vacuum and gravitation. This is identical in form with Einstein equations, but it is only in form. We have noticed that the Equations (31) has different meaning with Einstein equations. In the Equation (31), 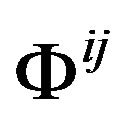 is the GGP and not a metric tensor now; R is an object constructing from the GGP and not a curvature of a Riemannian space-time! Later we can see that even the divergence of both sides of the equations in terms of the Minkowski metric
is the GGP and not a metric tensor now; R is an object constructing from the GGP and not a curvature of a Riemannian space-time! Later we can see that even the divergence of both sides of the equations in terms of the Minkowski metric 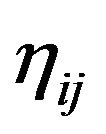 do not equal to zero, but Einstein equations do in the Riemannian space-time (covariant divergence). However, the Equation (31) can still be called Einstein equations. Just keeping in mind, the meaning has changed.
do not equal to zero, but Einstein equations do in the Riemannian space-time (covariant divergence). However, the Equation (31) can still be called Einstein equations. Just keeping in mind, the meaning has changed.
4.4. The Essential Significance of the de Donder Conditions
The conditions
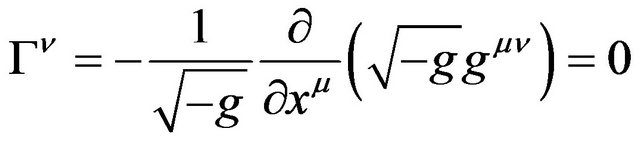 (32)
(32)
were introduced by de Donder [27]. This is equivalent to
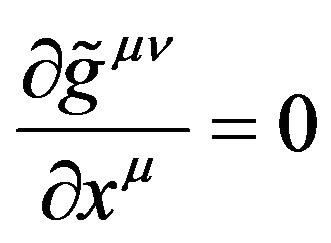 , (33)
, (33)
here  is the contravariant tensor density of the Riemannian metric
is the contravariant tensor density of the Riemannian metric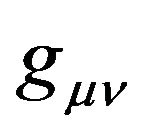 . Putting forward the de Donder conditions (Fock called it the harmonic conditions [28]) is only for convenient purposes and the conditions has no physical meaning. This is mainly owing to that, in General Relativity, the coordinates have no physical meaning. This is mainly owing to that the coordinates have no physical meaning in General Relativity. Therefore, the de Donder conditions also have no physical meaning.
. Putting forward the de Donder conditions (Fock called it the harmonic conditions [28]) is only for convenient purposes and the conditions has no physical meaning. This is mainly owing to that, in General Relativity, the coordinates have no physical meaning. This is mainly owing to that the coordinates have no physical meaning in General Relativity. Therefore, the de Donder conditions also have no physical meaning.
Fock [28] (pp. 342-349) had proven that the harmonic conditions together with the requirement of Euclidean behavior at infinity and with the condition ensuring uniqueness of a wave type solution can determine the harmonic coordinate system uniquely and the most general form of transformation from one system of the harmonic coordinates to another is the Lorentz transformation. In describing problems of the island type, Fock as much as considered the harmonic conditions in terms of the global Cartesian coordinates. However, Fock had not completely got rid of the fetter of the geometric theory of gravitation and comprehended its essential significance. He could not find a global Cartesian coordinate system in the Riemannian space-time. He merely called the Cartesian coordinates, which he found through the de Donder conditions together with the requirement of Euclidean behavior at infinity, the harmonic coordinates.
Yi-Shi Duan et al. [29] had also proven, for the system of the island matter, considering the harmonic conditions together with the requirement of Euclidean behavior at infinity, 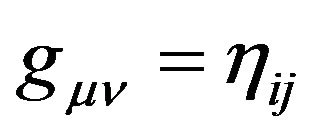 , when the gravitational field vanish, the coordinates become to the global Cartesian coordinates.
, when the gravitational field vanish, the coordinates become to the global Cartesian coordinates.
In my opinion, by adopting the harmonic conditions together with the requirement of Euclidean behavior at infinity actually is equal to require Einstein equations to be solved in a Minkowski space-time in an inertial reference frame and to choose a global Cartesian coordinate system. Pei-Yuan Chou [26] has clearly proposed that putting Einstein equations together with the harmonic conditions into a Minkowski space-time to solve gravitational problems is possible. He had found many solutions, such as the static fields of the spherical mass, the infinite rod with uniform linear density of matter, and the infinite plane with uniform surface distribution of matter. It is a pity he did not know why this method works. The Cartesian coordinates which Fock found are the global Cartesian coordinates and the Lorentz transformation is the global Lorentz transformation between two inertial reference frames.
We can see, Einstein equations and the gravitational field Equation (31) in form are completely same, and it cannot be solved by only using themselves because the field equations have four freedom components owing to the identical equations. It can be interpreted as the equations in arbitrary space-time including the Riemannian space-time. A solution which satisfies Einstein equations after being transferred through any real transformation of coordinates is still the solution of the equations. Due to this reason, when we face a large number of solutions in General Relativity, we often do not know how to deal with them and which one is true. Adopting the de Donder conditions together with the requirement of Euclidean behavior at infinity is equivalent to desorb the Einstein equations into a Minkowski space-time and choosing Cartesian coordinate system to solve. After using the de Donder conditions, the solution of Einstein equations is determined and only interpreted as the GGP in the inertial reference frames with Cartesian coordinates. Furthermore, Einstein equations satisfy the global Lorentz transformation between inertial reference frames. The coordinates called the harmonic coordinates are actually not only one, but a series of the inertial reference frames with Cartesian coordinate system. When we calculate the physical problem, we can choose one of them by using some boundary conditions.
We adopt the de Donder conditions
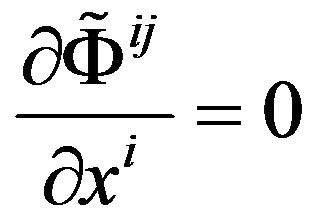 , (34)
, (34)
together with the requirement of Euclidean behavior at infinity to confine the Equation (31) in the Minkowski space-time, moreover with global Cartesian coordinates. After adopting the formula (34), we can absolutely certain of the meaning of the Equation (31) in mathematics, because the Equation (31) is completely identical in mathematical form with Einstein equations in the sense of Riemannian space-time. We consider the de Donder conditions (34) as the equations appended on the Equations (31).
4.5. The Equations of Gravitation Field
According to previous discussion, we can obtain the gravitational equations in an inertial reference frame with Cartesian coordinates. It can be written down like the conventional form (write 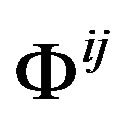 as
as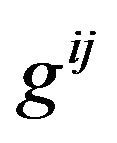 ),
),
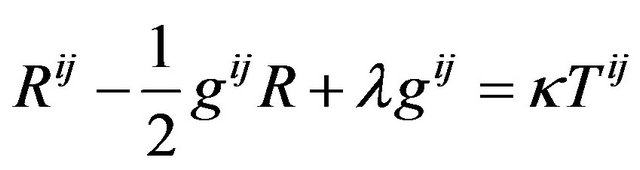 , (35)
, (35)
 . (36)
. (36)
Here 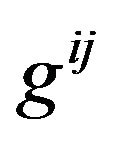 is the inverse GGP tensor;
is the inverse GGP tensor; 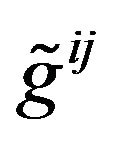 is the tensor density of
is the tensor density of ; i and j take 0, 1, 2, 3, denote that the tensor is in the Minkowski space-time with Cartesian coordinates.
; i and j take 0, 1, 2, 3, denote that the tensor is in the Minkowski space-time with Cartesian coordinates.
To generalize the Equations (35) and (36), we can obtain the general equations of gravitational field in any reference frame with arbitrary coordinates.
 , (37)
, (37)
 . (38)
. (38)
Here the semicolon “;” denotes the covariant derivatives with respect to flat space-time with arbitrary coordinate systems in any reference frame.
5. The Energy-Momentum Tensor of Gravitational Field and the Another Expression of the Equations of Gravitational Field
In the Riemannian space-time, we have the conservation law of energy-momentum (30). If ignoring the cosmology term, we have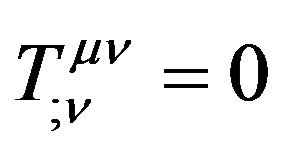 , Einstein (1915, 1918) [30] and Tolman (1930) [31] proposed:
, Einstein (1915, 1918) [30] and Tolman (1930) [31] proposed:
1) In GR, the gravitational field should own the energy-momentum which should have been included in the conservation law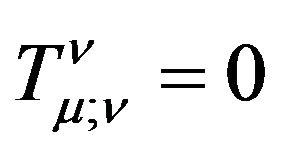 ;
;
2) we may change the covariant divergence equaling to zero to the normal divergence equaling to zero.
 , (39)
, (39)
in which  represent the energy-momentum of gravitational field, the comma “,” denotes the normal derivatives.
represent the energy-momentum of gravitational field, the comma “,” denotes the normal derivatives.
Many authors had tried to get the expression of the energy-momentum of gravitational field according to the point of view [24]. Now it is well known that it is impossible to find the tensor expression of the energy-momentum of pure gravitational field, because Einstein’s Equivalence Principle (EEP) [2,16]. 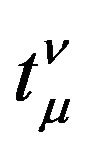 is energymomentum tensor of the matter except of the gravitational field.
is energymomentum tensor of the matter except of the gravitational field. 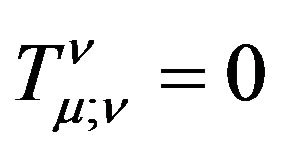 contain at most the coupling of matter and gravitational field or space-time. The gravitational field as a kind of entity of matter should not rely on the coordinate systems and the reference frames which we choose to describe it. The energy-momentum of gravitational field should be expressed by a tensor, while this is impossible in all metric theory of gravitation. Actually, this problem is inevitable because in GR the gravitational field is not regarded as a kind of entity of matter and replaced by the concept of the Riemannian space-time. The gravitational field is absorbed by the coordinates of space-time. The characteristics of the gravitational field are interpreted as the properties of space-time. In GR, we calculate the energy-momentum of gravitational field essentially is to take account of the energy-momentum of Riemannian space-time. Does the space-time itself have the energy-momentum? How to calculate the energy-momentum of the Minkowski spacetime? Actually, when we regard the gravitational field as the Riemannian space-time, namely geometrization of gravitation, the energy-momentum of gravitational field vanishes. We cannot express it. Even though the tensor of the energy-momentum of gravitational field is found, it must equal to zero due to the EP.
contain at most the coupling of matter and gravitational field or space-time. The gravitational field as a kind of entity of matter should not rely on the coordinate systems and the reference frames which we choose to describe it. The energy-momentum of gravitational field should be expressed by a tensor, while this is impossible in all metric theory of gravitation. Actually, this problem is inevitable because in GR the gravitational field is not regarded as a kind of entity of matter and replaced by the concept of the Riemannian space-time. The gravitational field is absorbed by the coordinates of space-time. The characteristics of the gravitational field are interpreted as the properties of space-time. In GR, we calculate the energy-momentum of gravitational field essentially is to take account of the energy-momentum of Riemannian space-time. Does the space-time itself have the energy-momentum? How to calculate the energy-momentum of the Minkowski spacetime? Actually, when we regard the gravitational field as the Riemannian space-time, namely geometrization of gravitation, the energy-momentum of gravitational field vanishes. We cannot express it. Even though the tensor of the energy-momentum of gravitational field is found, it must equal to zero due to the EP.
If 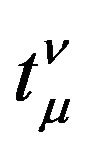 represent the energy-momentum of gravitational field, it should be a tensor and satisfy the coordinate transformations between arbitrary real reference frames. So
represent the energy-momentum of gravitational field, it should be a tensor and satisfy the coordinate transformations between arbitrary real reference frames. So 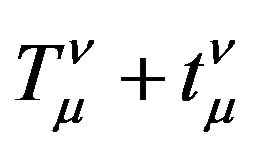 should satisfy the covariant divergence equal zero, namely
should satisfy the covariant divergence equal zero, namely
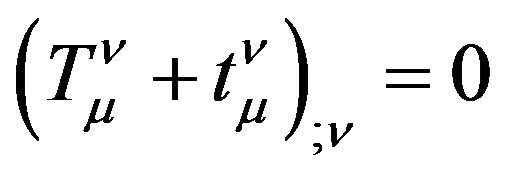 , (40)
, (40)
while not merely satisfy the normal divergence equal to zero.
Fock [28] (p. 328), by adopting the harmonic conditions and Einstein equations, obtained following equations:
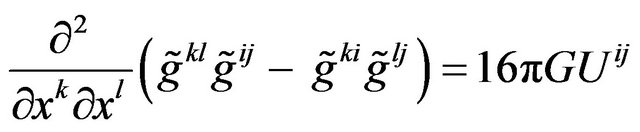 , (41)
, (41)
where
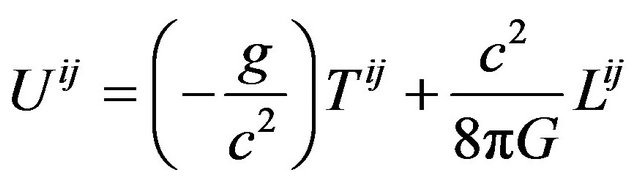 , (42)
, (42)
 , (43)
, (43)
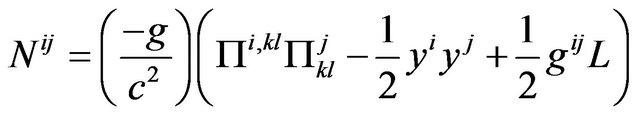 , (44)
, (44)
 , (45)
, (45)
and the quantities are defined as follow:
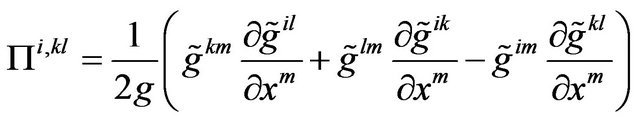 , (46)
, (46)
 , (47)
, (47)
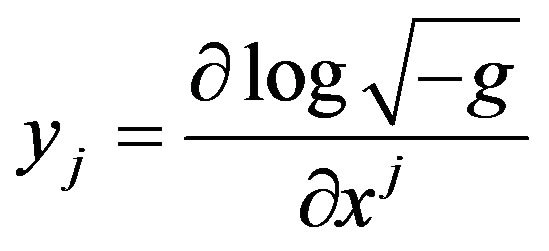 , (48)
, (48)
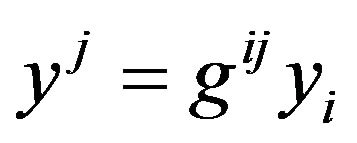 . (49)
. (49)
In the Equation (41), on the left, the expression of form is the Krutkov tensor [32]; the sum of the derivatives with respect to  of the left-hand side is identically zero. Therefore we have
of the left-hand side is identically zero. Therefore we have
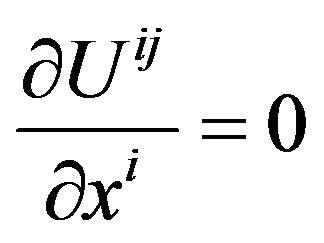 . (50)
. (50)
Fock noticed [28] (p. 329), the set of quantities  is not a generally covariant tensor. It is a tensor only with respect to linear transformation; in particular
is not a generally covariant tensor. It is a tensor only with respect to linear transformation; in particular 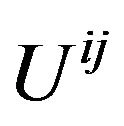 is a tensor in a harmonic coordinate system. The second term in (42) multiplied by
is a tensor in a harmonic coordinate system. The second term in (42) multiplied by  can be interpreted as the energy tensor of the gravitational field and the first term multiplied by
can be interpreted as the energy tensor of the gravitational field and the first term multiplied by  as the energy tensor of the material media and all fields other than gravitational field. If other than harmonic systems of coordinates are also admitted such an interpretation will not be completely unique if the region of the mass system is considered. But at large distances from masses, where the space-time is nearly pseudo-Euclidean and the coordinates are, by choice, Galilean, the physical meaning of the
as the energy tensor of the material media and all fields other than gravitational field. If other than harmonic systems of coordinates are also admitted such an interpretation will not be completely unique if the region of the mass system is considered. But at large distances from masses, where the space-time is nearly pseudo-Euclidean and the coordinates are, by choice, Galilean, the physical meaning of the 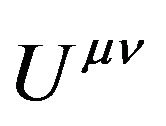 become unique in any case.
become unique in any case.
In General Relativity or the geometric theory of gravitation, Fock’s above conclusions make people uncomfortable and perplexed, because the total energy-momentum  should be a tensor with respect to arbitrary coordinate transformation between the reference frames. It’s the other way around, according to my point of view, the conclusions rightly exhibit that combining the harmonic conditions and Einstein equations is equivalent to desorb the GGP tensor from a Riemannian space-time to a Minkowski space-time and choosing the global Cartesian coordinates. After adopting the de Donder conditions (the harmonic conditions) in Einstein equations, the Equation (41) that Fock deduced are exactly the equations of gravitational field in the Minkowski space-time with a global Cartesian coordinates in an inertial reference frame. That is why the set of quantities
should be a tensor with respect to arbitrary coordinate transformation between the reference frames. It’s the other way around, according to my point of view, the conclusions rightly exhibit that combining the harmonic conditions and Einstein equations is equivalent to desorb the GGP tensor from a Riemannian space-time to a Minkowski space-time and choosing the global Cartesian coordinates. After adopting the de Donder conditions (the harmonic conditions) in Einstein equations, the Equation (41) that Fock deduced are exactly the equations of gravitational field in the Minkowski space-time with a global Cartesian coordinates in an inertial reference frame. That is why the set of quantities 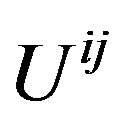 is the tensor only with respect to linear transformation. If we choose c = 1, it is clearly to see that
is the tensor only with respect to linear transformation. If we choose c = 1, it is clearly to see that 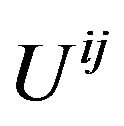 is the total energy-momentum tensor of the matter and the gravitational field except of the vacuum energy;
is the total energy-momentum tensor of the matter and the gravitational field except of the vacuum energy; 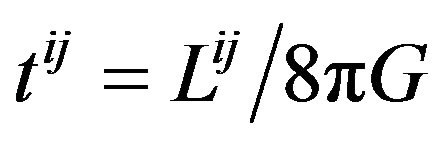 is exactly the pure energy-momentum tensor of gravitational field;
is exactly the pure energy-momentum tensor of gravitational field; 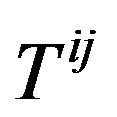 is the energy-momentum tensor of the material media and all fields other than gravitational field and its coupling with gravitational field. The coupling of matter and gravitation field is embodied in that we replace the metric tensor of a Minkowski space-time
is the energy-momentum tensor of the material media and all fields other than gravitational field and its coupling with gravitational field. The coupling of matter and gravitation field is embodied in that we replace the metric tensor of a Minkowski space-time 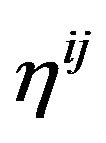 by using the GGP
by using the GGP 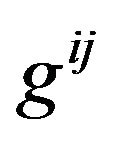 in the expression of
in the expression of . The Equation (50) are the conservation law in the Minkowski space-time with Cartesian coordinate. The equations and tensors all satisfy the global Lorentz covariance. We must emphasis that we have the Equations (25) and (30) in the Riemannian space-time , but after being desorbed to the Minkowski space-time,
. The Equation (50) are the conservation law in the Minkowski space-time with Cartesian coordinate. The equations and tensors all satisfy the global Lorentz covariance. We must emphasis that we have the Equations (25) and (30) in the Riemannian space-time , but after being desorbed to the Minkowski space-time,
 and
and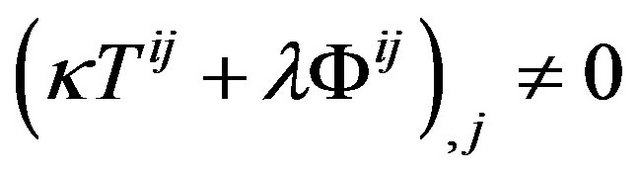 because we have to consider the energy-momentum of gravitational field in the conservation law. However, the Equation (31) desorbed from the Riemannian space-time, itself has already contained the energy-momentum of gravitational field.
because we have to consider the energy-momentum of gravitational field in the conservation law. However, the Equation (31) desorbed from the Riemannian space-time, itself has already contained the energy-momentum of gravitational field.
To generalize the Equation (41) to be general covariant (note: this is the different notion from GR) equations with respect to arbitrary coordinate in inertial and noninertial reference frames, and also consider the cosmology term (background vacuum energy), we obtain the general covariant equations of gravitational field
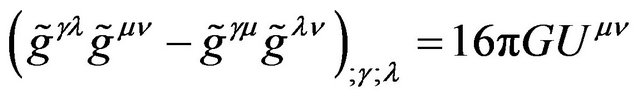 , (51)
, (51)
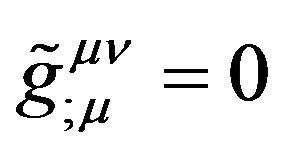 . (52)
. (52)
Here the semicolon “;” denotes the covariant derivatives with respect to the space-time metric  of an arbitrary reference frame. The tensorial de Donder conditions are the component element of whole equations of gravitational field. The conservation law of the total energy-momentum of all of matter, including the material media, all field and vacuum energy:
of an arbitrary reference frame. The tensorial de Donder conditions are the component element of whole equations of gravitational field. The conservation law of the total energy-momentum of all of matter, including the material media, all field and vacuum energy:
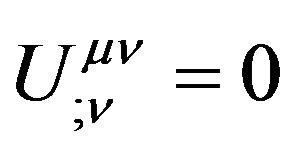 , (53)
, (53)
where
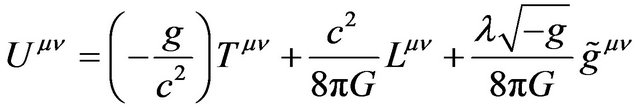 . (54)
. (54)
Here  is the cosmology constant. The Equations (51) and (52) are equivalent to the Equations (37) and (38).
is the cosmology constant. The Equations (51) and (52) are equivalent to the Equations (37) and (38).
6. The Space-Time of Gravitational Field
6.1. The Significance of Coordinates
The coordinates are only introduced as the parameters in General Relativity. They hold no physical significance. This is inconceivable. The coordinates which we used to describe the motion of matter have no meaning! How is the motion of matter described? In my point of view, the coordinates have clearly physical significance.
For the formula
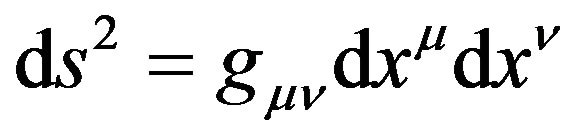 , (55)
, (55)
can be understood by two ways: firstly, ds can be understood as the GA line element consisting of a GGP tensor 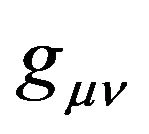 and a background space-time
and a background space-time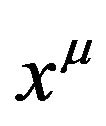 ; secondly, ds can be regarded as the line element of Riemannian space-time that is formed after the coordinates
; secondly, ds can be regarded as the line element of Riemannian space-time that is formed after the coordinates 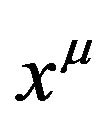 absorb the GGP tensor
absorb the GGP tensor  and the GGP tensor
and the GGP tensor 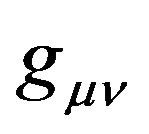 becomes the metric tensor. In the first situation, the coordinates have clear and practical measurable meaning, while in the second situation, the coordinates have lost its practical measurable meaning. In my point of view, the coordinates
becomes the metric tensor. In the first situation, the coordinates have clear and practical measurable meaning, while in the second situation, the coordinates have lost its practical measurable meaning. In my point of view, the coordinates 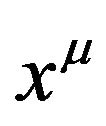 can be the Cartesian coordinates in a Minkowski space-time or the coordinates of background space-time in a non-inertial reference frame. According to the notion of the absorption operation, the coordinates in GR are merely the coordinate parameters, after the GGP tensor is absorbed by the coordinates of background space-time and become a metric tensor of a Riemannian space-time in Mathematics. Here the significance of the coordinates is completely different from that before absorbing.
can be the Cartesian coordinates in a Minkowski space-time or the coordinates of background space-time in a non-inertial reference frame. According to the notion of the absorption operation, the coordinates in GR are merely the coordinate parameters, after the GGP tensor is absorbed by the coordinates of background space-time and become a metric tensor of a Riemannian space-time in Mathematics. Here the significance of the coordinates is completely different from that before absorbing.
Formerly, when we solve Einstein equations, adopt the harmonic conditions and consider the Newton approximation in General Relativity, we are actually desorbing the gravitational field from the coordinates of the Riemannian space-time and are endowing the coordinates with the meaning of the coordinates of the flat space-time in the inertial reference frame. It is being routinely used in relativistic astrometry and relativistic celestial mechanics. People are well aware of the action of the gravitational field and are for more convenient and informative to store and analyze the data in terms of the flat space-time quantities after subtraction of the theoretically calculated gravitational corrections! rather than in terms of directly measured quantities. This is one of the reasons that Einstein equations can give a description of gravitational phenomena in agreement with observation!
6.2. The Meaning of the Line Element of Gravitational Action (GA) dA
In chapter 2, we have obtained the motion equations of a freely falling particle in a gravitational field (8) and (9) by using the variation
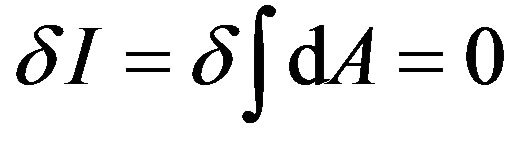 . (56)
. (56)
Here we can see that  represent the length of the trajectory of a freely falling particle in a gravitational field. Therefore, dA is the differential element of the length of a four dimensional trajectory. The trajectory is not a straight line, but a curve, due to the action of gravitation. Like an electron in an electromagnetic field, its trajectory has been deformed. dA is the differential element of the length of the curved four dimensional trajectory.
represent the length of the trajectory of a freely falling particle in a gravitational field. Therefore, dA is the differential element of the length of a four dimensional trajectory. The trajectory is not a straight line, but a curve, due to the action of gravitation. Like an electron in an electromagnetic field, its trajectory has been deformed. dA is the differential element of the length of the curved four dimensional trajectory.
Now we analyze the formula of the GA line element
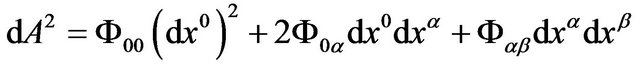 . (57)
. (57)
In the static gravitational field, 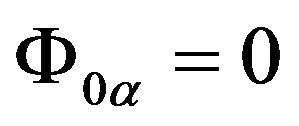 , then
, then
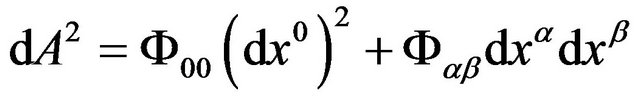 . (58)
. (58)
Therefore 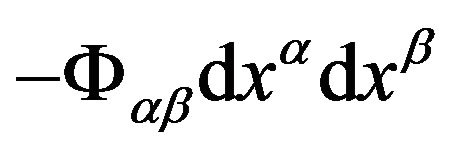 exactly represents the distance between two infinitely close points of a three dimensional trajectory in a gravitational field, using
exactly represents the distance between two infinitely close points of a three dimensional trajectory in a gravitational field, using 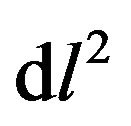 to denote, we have
to denote, we have
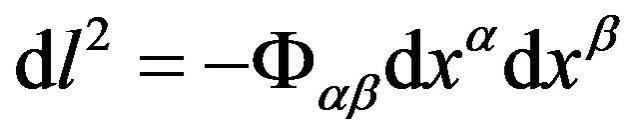 . (59)
. (59)
This is easy to understand that the freely falling particle is acted on by the gravitational force, its trajectory has been changed and is related to the gravitational field. Generally, its trajectory is no longer straight, but curved.
When a particle is at rest in a gravitational field, follow (58), takes , then we have
, then we have
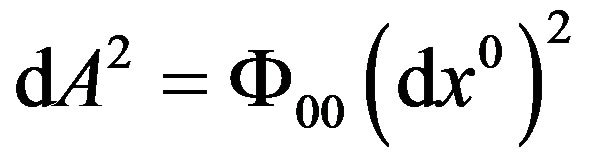 , (60)
, (60)
thereby, obtain
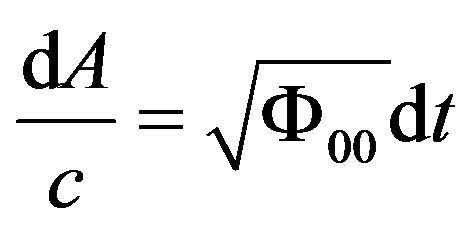 . (61)
. (61)
Take
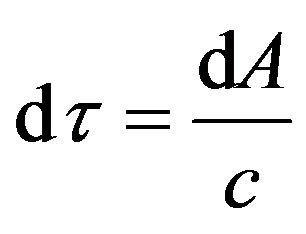 , (62)
, (62)
so
 . (63)
. (63)
 is called proper time in General Relativity and equal to the coordinate time in the freely falling local reference frame [24] (p. 26). What is the meaning of
is called proper time in General Relativity and equal to the coordinate time in the freely falling local reference frame [24] (p. 26). What is the meaning of 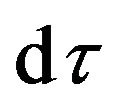 in my point of view? It is the pure time component of the curved trajectory in a four dimensional space-time. It represents the period of the motion of matter in the gravitational field. Once a particle enters into a gravitational field, it obtains gravitational potential and its kinetic energy is changed. The change of its energy also reflects in the variation of its time. We call this quantity as Effective Time. Using the effective time
in my point of view? It is the pure time component of the curved trajectory in a four dimensional space-time. It represents the period of the motion of matter in the gravitational field. Once a particle enters into a gravitational field, it obtains gravitational potential and its kinetic energy is changed. The change of its energy also reflects in the variation of its time. We call this quantity as Effective Time. Using the effective time 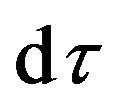 to replace the background coordinate time is equivalent to take account of the gravitational potential when we calculate the motion of a particle under the presence of gravitation. The effective time
to replace the background coordinate time is equivalent to take account of the gravitational potential when we calculate the motion of a particle under the presence of gravitation. The effective time 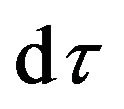 is the time of the real clock which is at rest in the gravitational field and affected by the gravitational field. The coordinate time dt is the time of the clock which is at rest in the space with no gravitational field or at infinity from the gravitational source. It can be measured by the freely falling clock, because
is the time of the real clock which is at rest in the gravitational field and affected by the gravitational field. The coordinate time dt is the time of the clock which is at rest in the space with no gravitational field or at infinity from the gravitational source. It can be measured by the freely falling clock, because 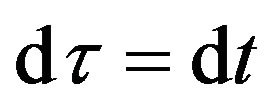 in the freely falling frame.
in the freely falling frame.
The energy of a freely falling particle in a steady gravitational field can be written as
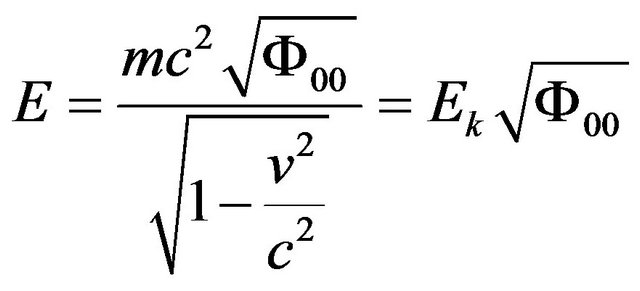 . (64)
. (64)
Here E is the total energy of the particle in the gravitational field; 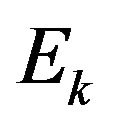 is the Relativistic Kinetic energy of the particle in the gravitational field. From the formula (63) and (64), we obtain
is the Relativistic Kinetic energy of the particle in the gravitational field. From the formula (63) and (64), we obtain
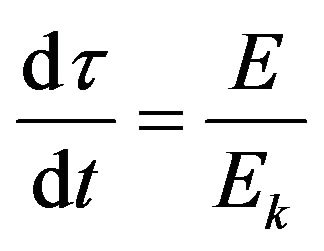 . (65)
. (65)
We see the relationship of energy and time. One step further, we gain
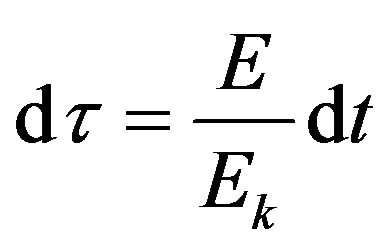 . (66)
. (66)
This indicates that the effective time 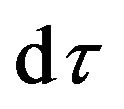 is caused by the variation of the gravitational potential energy. While the variation of the gravitational potential energy varies accompany with the variation of its kinetic energy. In Special Relativity, we know that the energy is the time component of the energy-momentum Tensor. The variation of energy reflects in the variation of time.
is caused by the variation of the gravitational potential energy. While the variation of the gravitational potential energy varies accompany with the variation of its kinetic energy. In Special Relativity, we know that the energy is the time component of the energy-momentum Tensor. The variation of energy reflects in the variation of time.
6.3. The Essence of the Gravitational Red Shift
For a photon, according to the formula (64), its energy in a static gravitational field is
 . (67)
. (67)
Here 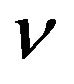 is the frequency of the photon, h is Plank constant. The formula (67) also can be derived from the formula (63). From the formula (63), we have
is the frequency of the photon, h is Plank constant. The formula (67) also can be derived from the formula (63). From the formula (63), we have
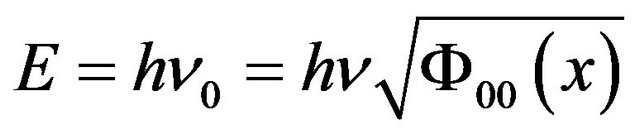 , (68)
, (68)
where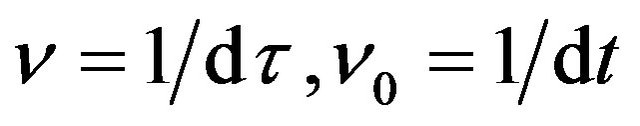 .
.  is the frequency of the photon at the point
is the frequency of the photon at the point 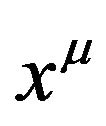 of the gravitational field.
of the gravitational field. 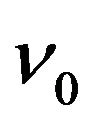 equals to the frequency of the same photon at infinity from the gravitational source or at the place with no gravitational field. The formula (68) tells us that the photon’s energy is conserved when the photon moves from infinity to the point
equals to the frequency of the same photon at infinity from the gravitational source or at the place with no gravitational field. The formula (68) tells us that the photon’s energy is conserved when the photon moves from infinity to the point 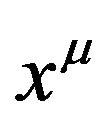 in the static gravitational field.
in the static gravitational field.
Therefore, at the point A of the gravitational field, a photon which has the frequency 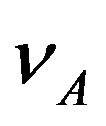 is transmitted, its total energy is
is transmitted, its total energy is
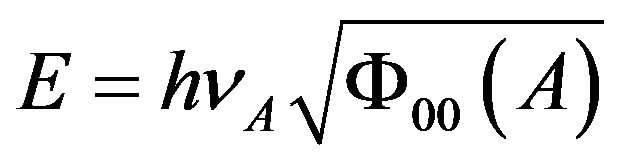 . (69)
. (69)
when the photon moves to point B, it has
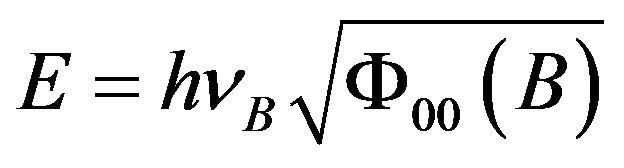 . (70)
. (70)
Even though the photon’s kinetic and potential energy has been changed during the motion in the gravitational field, the total energy conserved, namely
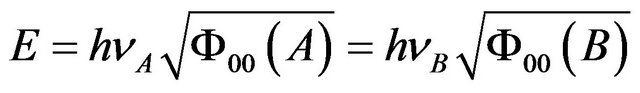 , (71)
, (71)
thereby
 . (72)
. (72)
Considering Newton’s approximation (4), adopt the Taylor spread and take the first level approximate, we arrive at
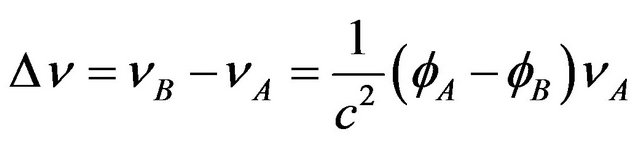 . (73)
. (73)
While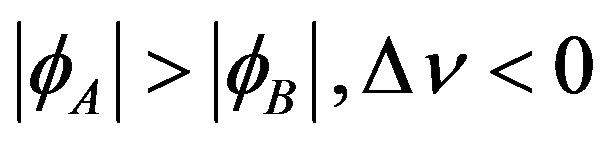 , This indicates that the spectrum observed at the point of weak gravitational field shifts to the red end of the spectrum when the light transmits from a point of strong gravitational field to a point of weak gravitational field. This is called the gravitational red shift [24].
, This indicates that the spectrum observed at the point of weak gravitational field shifts to the red end of the spectrum when the light transmits from a point of strong gravitational field to a point of weak gravitational field. This is called the gravitational red shift [24].
From the analysis above, we can conclude that the red shift of light is owing to the energy conservation of the photon and the transformations between the potential and kinetic energy during the motion in the gravitational field. As a photon moves from a strong gravitational field to a weak gravitational field, its potential energy increases whiles its kinetic energy decrease. Therefore, the frequency becomes slower and the wave length becomes longer, which is the gravitational red shift. This is the essence of the gravitational red shift. This comprehension is different with the geometric explanation.
7. Summary
So far, we have analyzed and elaborated the relationships of the Riemannian space-time, the de Donder conditions and the gravitational field in flat space-time through establishing the concepts of the absorption operation and the desorption operation. The A-D Operation completely adapt to the Equivalence Principle. The tensors are invariant under the A-D Operations. In the discussion, we have answered why the structural form of Einstein equations is correct even if it is obtained from the geometric interpretation that people feel uncomfortable. It is clear that Einstein equations and the de Dondle conditions as the equations of gravitational field can be used in a flat space-time to solve. The essential significance of the de Donder conditions is to desorb the tensor field of gravitation from the Riemannian space-time to the Minkowski space-time with the Cartesian coordinates. The gravitational field is true physical field like the electromagnetic field. Einstein geometric interpretation is a special case. The source of gravitational field is the energy-momentum of matter. This can be deduced from the fact that the gravitational mass and inertial mass are equal. The inverse of this deduction is also true. In this paper, the motion equations of particle and the equations of gravitational field in the inertial and non-inertial reference frames are established. The tensor expression of the gravitational field is found. It satisfied the global Lorentz Covariance and is also covariance with respect to the coordinate transformations between arbitrary inertial and non-inertial reference frames. It is clear that the problems of gravitation and of space-time in a non-inertial frame can be solved respectively. The gravitation field can be described by using Riemann geometry, but as we know, it is quite complicated and confusing, even can deduce some wrong conclusions. Gravitation can affect the motion of matter and change the energy-momentum of matter, thereby affect the period of matter’s motion, but these changes can be aware of by comparing with the background space-time. Just like usual, it is being routinely used in relativistic astrometry and relativistic celestial mechanics. People can store and analyze the data in terms of the flat space-time quantities after subtraction of the theoretically calculated gravitational corrections, rather than in terms of directly measured quantities. The effective time (or proper time) 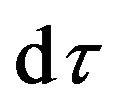 is the reflection of the change of particle energy in the gravitational field. The gravitational red-shift of light is due to the photon obeying the conservation law of energy and the potential and kinetic energy transforming between each other when it is moving in a gravitational field.
is the reflection of the change of particle energy in the gravitational field. The gravitational red-shift of light is due to the photon obeying the conservation law of energy and the potential and kinetic energy transforming between each other when it is moving in a gravitational field.
We know the GGP tensor 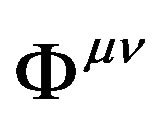 should be the function with respect to the metric tensor of space-time
should be the function with respect to the metric tensor of space-time 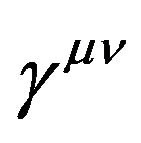 and real gravitational potential (GP) tensor
and real gravitational potential (GP) tensor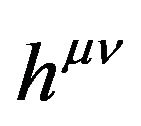 . Its relationship should be found through some empirical evidences or physical requirements.
. Its relationship should be found through some empirical evidences or physical requirements.
8. Acknowledgements
I am grateful to all my family members, colleagues and friends for their encouraging and support.
REFERENCES
- L. Smolin, “How Far Are We from the Quantum Theory of Gravity?” Reports on Progress in Physics, Vol. 72, No. 12, 2009, Article ID: 126002. doi:10.1088/0034-4885/72/12/126002
- L. M. Butcher, A. N. Lasenby and M. P. Hobson, “Physical Significance of the Babak-Grishchuk Gravitational Energy-Momentum Tensor,” Physical Review D, Vol. 78, No. 6, 2008, Article ID: 064034. doi:10.1103/PhysRevD.78.064034
- N. Rosen, “General Relativity and Flat Space I,” Physical Review, Vol. 57, No. 2, 1940, pp. 147-150. doi:10.1103/PhysRev.57147
- R. Kraichnan, “Special-Relativistic Derivation of Generally Covariant Gravitation Theory,” Physical Review, Vol. 98, No. 4, 1955, pp. 1118-1122.. doi:10.1103/PhysRev.98.1118
- S. N. Gupta, “Einstein’s and Other Theories of Gravitation,” Reviews of Modern Physics, Vol. 29, No. 3, 1957, pp. 334-336. doi:10.1103/RevModPhys.29.334
- W. Thirring, “An Alternative Approach to the Theory of Gravitation,” Annals of Physics, Vol. 16, No. 1, 1961, pp. 96-117. doi:10.1016/0003-4916(61)90182-8
- S. Weinberg, “Derivation of Gauge Invariance and the Equivalence Principle from Lorentz Invariance of the S-Matrix,” Physics Letters, Vol. 9, No. 4, 1964, pp. 357- 359. doi:10.1016/0031-9163(64)90396-8
- V. I. Ogievetsky and I. V. Polubarinov, “Interacting Field of Spin 2 and the Einstein Equations,” Annals of Physics, Vol. 35, No. 2, 1965, pp. 167-208. doi:10.1016/0003-4916(65)90077-1
- S. Deser, “Self-Interaction and Gauge Invariance,” General Relativity and Gravitation, Vol. 1, No. 1, 1970, pp. 9- 18. doi:10.1007/BF00759198
- P. van Nieuwenhuizen, “On Ghost-Free Tensor Lagrangians and Linearizes Gravitation,” Nuclear Physics B, Vol. 60, 1973, pp. 478-492. doi:10.1016/0550-3213(73)90194-6
- T. M. Nieuwenhuizen, “Einsein vs Maxwell: Is Gravitation a Curvature of Space, a Field in Flat Space, or Both?” Europhysical Letters, Vol. 78, 2007, p. 10010. doi:10.1209/0295-5075/78/10010
- D. G. Boulware and S. Deser, “Classical General Relativity Derived from Quantum Gravity,” Annals of Physics, Vol. 89, No. 1, 1975, pp. 193-240. doi:10.1016/0003-4916(75)90302-4
- L. P. Grishchuk, A. N. Petrov and A. D. Popova, “Exact Theory of the (Einstein) Gravitational Field in an Arbitrary Background Space-Time,” Communications in Mathematical Physics, Vol. 94, No. 3, 1984, pp. 379-396. doi:10.1007/BF01224832
- A. A. Logunov and M. A. Mestvirishvili, “The Fundamental Principles of the Relativistic Theory of Gravitation,” Theoretical and Mathematical Physics, Vol. 86, No. 1, 1991, pp. 1-9. doi:10.1007/BF01018491
- M. Visser, “Mass for the Graviton,” General Relativity and Gravitation, Vol. 30, No. 12, 1998, pp. 1717-1728. doi:10.1023/A:1026611026766
- S. V. Babak and L. P. Grishchuk, “Energy-Momentum Tensor for the Gravitational Field,” Physical Review D, Vol. 61, No. 2, 1999, Article ID: 024038. doi:10.1103/PhysRevD.61.024038
- J. B. Pitts and W. C. Schieve, “Slightly Bimetric Gravitation,” General Relativity and Gravitation, Vol. 33, No. 8, 2001, pp. 1319-1350. doi:10.1023/A:1012005508094
- L. P. Grishchuk, “Some Uncomfortable Thoughts on the Nature of Gravity, Cosmology, and the Early Universe,” Space Science Reviews, Vol. 148, No. 1-4, 2009, pp. 315- 328. doi:10.1007/s11214-009-9509-6
- E. R. Huggins, Ph.D. Thesis, California Institute of Technology, Pasadena, 1962.
- R. P. Feynman, F. Morinigo, W. Wagner and B. Hatfield, “Feynman Lectures on Gravitation,” Addison Wesley, Boston, 1995.
- A. A. Logunov, “The Relativistic Theory of Gravitation,” Nauka, Moscow, 2000.
- L. V. Verozub, “Gravitation as Field and Curvature,” Gravitation, Cosmology and Relativistic Astrophysics, Collection of papers, Kharkov National University, 2001, p. 159.
- T. Padmanabhan, “From Gravitons to Gravity: Myths and Reality,” International Journal of Modern Physics D, Vol. 17, No. 03n04, 2008, p. 367. doi:10.1142/S0218271808012085
- L. Liu, “General Relativity,” Advanced Education Publishing Company, Beijing, 1987, p. 133.
- R. V. Eotvos, D. Pekar and E. Fekete, Annals of Physics, Vol. 68, 1922, p. 11.
- P.-Y. Chou, “On the Physical Significance of Coordinates and the Solutions of the Field Equations in Einstein’s Theory of Gravitation,” Scientia Sinica (Series A), Vol. XXV, No. 6, 1982, pp. 628-643. http://www.cnki.com.cn/Article/CJFDTotal-JAXK198204005.htm http://www.emw21.com/CTS/Global%20Chinese/ZhouPY/ZhouPYFrame.htm
- T. de Donder, “La Gravifique Einsteinienne,” University of Michigan Library, Paris, 1921.
- V. Fock, “The Theory of Space Time and Gravitation,” Pergamon Press, New York, 1959, p. 175.
- Y.-S. Duan and J.-Y. Zhang, “On Fock’s Harmonic Conditions in General Relativity,” Acta Physica Sinica, Vol. 18, No. 4, 1962, p. 211. http://www.oaj.cas.cn/cn
- A. Einstein, “Der Energiesatz in der allgemeinen Relativitätstheorie,” Königlich Preußische Akademie der Wissenschaften (Berlin), Sitzungsberichte, 1918, p. 448-459.
- R. Tolman, “On the Use of the Energy-Momentum Principle in General Relativity,” Physical Review, Vol. 35, No. 8, 1930, pp. 875-895. doi:10.1103/PhysRev.35.875
- Y. A. Krutkov, “The Stress Tensor and the Solution of General Problems in the Static Theory of Elasticity,” Akad Nauk, U.S.S.R., 1949.

