International Journal of Astronomy and Astrophysics
Vol.02 No.01(2012), Article ID:18173,13 pages
10.4236/ijaa.2012.21002
Revised Newtonian Formula of Gravity and Equation of Cosmology in Flat Space-Time Transformed from Schwarzschild Solution
Xiaochun Mei, Ping Yu
Institute of Innovative Physics in Fuzhou, Department of Physics, Fuzhou University, Fuzhou, China
Email: ycwlyjs@yeah.net, yupingpingyu@yahoo.com
Copyright © 2016 by author and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received January 3, 2012; revised February 7, 2012; accepted February 16, 2012
ABSTRACT
By transforming the geodesic equation of the Schwarzschild solution of the Einstein’s equation of gravity field to flat space-time for description, the revised Newtonian formula of gravity is obtained. The formula can also describe the motion of object with mass in gravity field such as the perihelion precession of the Mercury. The space-time singularity in the Einstein’s theory of gravity becomes the original point r = 0 in the Newtonian formula of gravity. The singularity problem of gravity in curved space-time is eliminated thoroughly. When the formula is used to describe the expansive universe, the revised Friedmann equation of cosmology is obtained. Based on it, the high red-shift of Ia supernova can be explained well. We do not need the hypotheses of the universe accelerating expansion and dark energy again. It is also unnecessary for us to assume that non-baryon dark material is 5 - 6 times more than normal baryon material in the universe if they really exist. The problem of the universal age can also be solved well. The theory of gravity returns to the traditional form of dynamic description and becomes normal one. The revised equation can be taken as the foundation of more rational cosmology.
Keywords:
General Relativity; Schwarzschild Metric; Cosmology; Friedmann Equation; Newtonian Gravity; Supernova; Hubble Constant; Dark Material; Dark Energy; Universe Accelerating Expansion; Universe Age
1. Introduction
Established on the foundation of curved space-time, Einstein’s theory of gravity is the dominate theory at present. However, Einstein’s theory has some difficulties hard to be overcome such as the problems of normalization, singu- larity and uniqueness of gravity field’s energy and so on. In addition, it is difficulty to solve the non-linear Einstein’s equation of gravity field. It is always attractive to reestablish the theory of gravity in flat space-time without these troubles. Since the 1940’s, many people has tried and many theories had been proposed [1,2]. These theories are consistent with Einstein’s one under the condition of weak fields, but are different in strong fields. Meanwhile, these theories also have some problems hard to be overcome.
The standard theory of cosmology faces many principle difficulties at present. As is proved below, the problems originate from the Friedmann equation which is unsuitable to describe the high speed expansion of the universe. The reason is that two simplified and improper conditions were used in the deduction of the Friedmann equation. They are the R-W metric and static energy momentum tensor. At present, the R-W metric is considered with
constant spatial curvature. However, the author had proved that strictly based on the curvature formula of the Riemannian geometry, when the scalar factor R(t) changes with time, the R-W metric has no constant curvature [3]. The common understanding about the spatial curvature of the R-W metric is wrong. This idea would impose great influence on cosmology. Due to this result, many conclusions in the cosmology such as the densities of dark material and dark energy should be re-estimated.
It is proved further in this paper that the R-W metric leads to the Galileo’s transformation of light’s velocity, instead of the Einstein’s transformation. So the R-W metric is not relativity metric and unsuitable to be taken as the basic space-time framework of modern cosmology.
Meanwhile, because relative velocities exist between materials and observers in the expansive universe, the equation of cosmology should use dynamic energy momentum tensor, rather than static one as commonly used in the current cosmology.
In fact, E. A. Milne pointed out in 1943 that the Friedmann equation of cosmology could be deduced based on the Newtonian formula of gravity [4]. It means that the Friedmann equation is equivalent to the Newtonian theory actually. It is only suitable for describing the process of low speed expansion of the universe, but not for the process of high speed expansion.
However, it is proved in this paper that if dynamic energy momentum tensor is used, the equation of cosmology would become very complex, so that it can not be solved actually. The pioneer of cosmology must have considered this problem and had to use static energy momentum tensor. In the early stage of cosmology, the Friedmann equation seemed to be appreciable because the expansive speed observed was low. When cosmology develops to present level, we observe the high speed expansion. In this case, the Friedmann equation becomes unsuitable for the problems such as the high red-shift of supernova. We have to find more precise method to describe them.
It is proved in this paper that by transforming the geodesic equation of the Schwarzschild solution of the Einstein’s equation of gravity field to flat space-time, the re- vised Newtonian formula of gravity can be obtained. The formula can well describe the perihelion precession of the Mercury. The space-time singularities in the Einstein’s theory of gravity become the point r = 0 in the revised New- tonian formula of gravity. We have no the trouble of singularities again.
When the revised formula is used to describe the expansive universe, we obtain the revised Friedmann equation. Based on it, the high red-shift of supernova can be explained well without the hypotheses of the universal accelerating expansion and dark energy. Many problems in- cluding the universe age to be too small can also be resolved well. In this way, we can get rid of the current puzzle situation of cosmology completely.
2. Revised Newtonian Formula of Gravity Based on the Schwarzschild
2.1. Revised Newtonian Formula of Gravity
According to general relativity, the Schwarzschild metric (external solution) is
 (1)
(1)
Here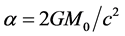 . Let
. Let 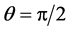 and substitute (1) into the equation of geodetic line, we have the integrals
and substitute (1) into the equation of geodetic line, we have the integrals
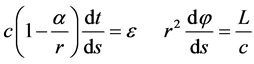 (2)
(2)
Here 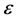 and
and 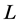 are constants. By cancelling
are constants. By cancelling  from the formulas, we can obtain
from the formulas, we can obtain
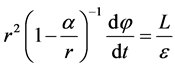 (3)
(3)
We define
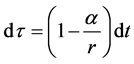 (4)
(4)
In which 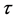 is eigen time,
is eigen time, 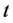 is coordinate time. Then, let
is coordinate time. Then, let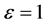 , we have from (2)
, we have from (2)
 (5)
(5)
Then, (3) becomes
 (6)
(6)
Here  is the angular momentum of unit mass. (6) is just the conservation formula of angel momentum.
is the angular momentum of unit mass. (6) is just the conservation formula of angel momentum.
We only discuss the motion of particles with mass in gravitational field. By considering (6), we write (1) as
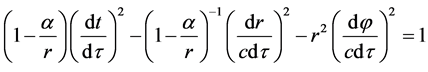 (7)
(7)
By considering (4) and (6), the formula above can be written as
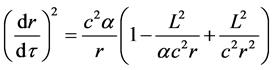 (8)
(8)
Taking the differential of (8) about , we get
, we get
 (9)
(9)
Note that all quantities in (9) are defined in curved space-time. According to the theory of the non-Euclidean geometry, although we can not transform whole metric of curved space-time into that of flat space-time in general, we can always transform the geodetic line described in curved space-time into that in flat space. Let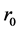 ,
, 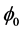 and
and 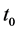 represent the space-time coordinates of flat space-time, due to the invariability of
represent the space-time coordinates of flat space-time, due to the invariability of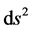 , we have
, we have
 (10)
(10)
We see that the forms of third items on the two sides of the second equal sign of the formula above are completely the same. So we can take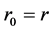 ,
, 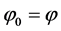 and get the relation between times
and get the relation between times 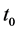 and
and 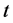
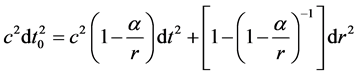 (11)
(11)
by considering (4), we get and from (8)
 (12)
(12)
Substituting it into (11), we get
 (13)
(13)
Comparing with (4), we have
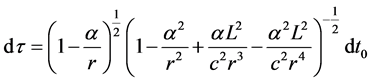 (14)
(14)
Because we have taken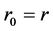 , all quantities on the right side of (14) have been defined in flat space-time. Note that in the classical Newtonian theory of gravity, at the directions of
, all quantities on the right side of (14) have been defined in flat space-time. Note that in the classical Newtonian theory of gravity, at the directions of 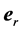 and
and 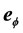 in plane polar coordinates system, the partial motion equations of unit mass are individually
in plane polar coordinates system, the partial motion equations of unit mass are individually
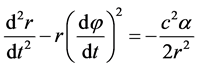 (15)
(15)
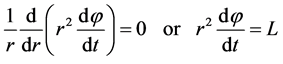 (16)
(16)
Substitute (16) into (15), we get
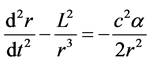 (17)
(17)
Comparing with (9) and let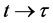 , except the revised item in the bracket of (9), we see that the forms of (9) and (17) are completely similar. So we can write (9) as the following vector equation
, except the revised item in the bracket of (9), we see that the forms of (9) and (17) are completely similar. So we can write (9) as the following vector equation
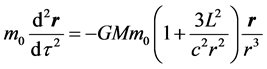 (18)
(18)
Let  and consider (6), the formula above can be transformed to
and consider (6), the formula above can be transformed to
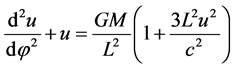 (19)
(19)
This formula is the one used to describe the perihelion precession of the Mercury in general relativity. In the deduction process above, we use the equation of geodetic line (2). It means that we transform the equation of geodetic line into the revised formula of the Newtonian gravity, in stead of transforming whole curved space-time to flat space-time. But it is enough for us to describe an object’s motion in gravity field.
Now let’s prove that the effect of special relativity has been taken into account in (18). From (8), (12) and (14), we can obtain
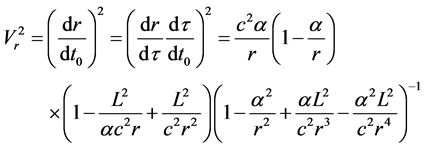 (20)
(20)
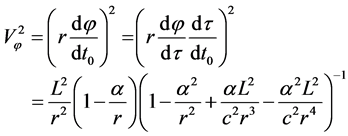 (21)
(21)
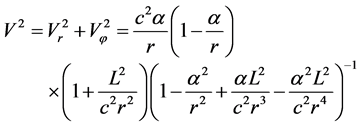 (22)
(22)
 (23)
(23)
Comparing with (14), we get
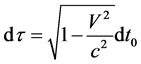 (24)
(24)
This is just the formula of time delay in special relativity. The result verifies the rationality of (18). Let 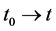 at last, we write (18) as
at last, we write (18) as
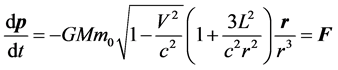 (25)
(25)
It is the revised Newtonian formula of gravity based on general relativity. In the formula, 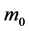 is the static mass of moving particle and the center static mass
is the static mass of moving particle and the center static mass 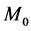 has spherical symmetry. Angle momentum makes gravity larger but speed makes it smaller. The result is equivalent to replace particle’s static mass with following effective mass in the Newtonian theory
has spherical symmetry. Angle momentum makes gravity larger but speed makes it smaller. The result is equivalent to replace particle’s static mass with following effective mass in the Newtonian theory
 (26)
(26)
We can call m as the motion mass of gravity which is related to object’s speed and angle momentum.
2.2. The Motion of Particle in Gravitational Field with Spherical Symmetry
For simplicity, we only discuss the motion of a particle moves along the radius vector direction with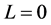 . In this case, by considering (23), (25) becomes
. In this case, by considering (23), (25) becomes
 (27)
(27)
by multiplying  on both sides of (27), the potential energy of the particle in gravitational field is
on both sides of (27), the potential energy of the particle in gravitational field is
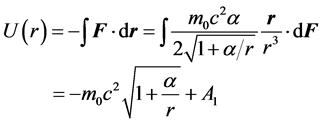 (28)
(28)
The dynamic energy of particle is
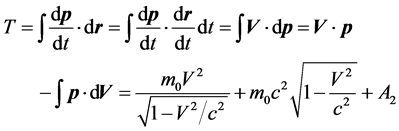 (29)
(29)
when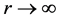 , we have
, we have 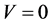 and
and . So the law of energy conservation of a particle in the gravitational field can be written as
. So the law of energy conservation of a particle in the gravitational field can be written as
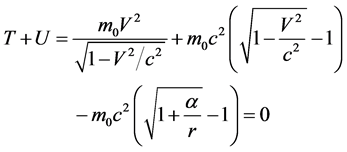 (30)
(30)
when 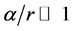 and
and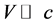 , we get the classic law of energy conservation in the Newtonian theory of gravity
, we get the classic law of energy conservation in the Newtonian theory of gravity
 (31)
(31)
In the situation of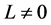 , we calculate the problem in the weak field with
, we calculate the problem in the weak field with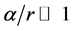 . By keeping items with the orders up to
. By keeping items with the orders up to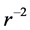 , we have
, we have
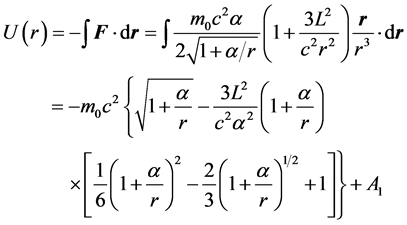 (32)
(32)
So the law of energy conservation is
 (33)
(33)
Here E is a constant.
Now let’s discuss the motion of a particle in the gravity field. Suppose that a particle falls freely along the radium direction of gravity field, its velocity and acceleration are individually
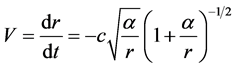 (34)
(34)
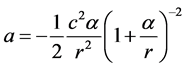 (35)
(35)
when , we have
, we have  and
and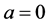 . Suppose that the particle is at point
. Suppose that the particle is at point 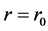 when
when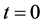 , by the integral of (34), we get
, by the integral of (34), we get
 (36)
(36)
It is obvious that every thing is normal within the region . The particle is monotonously accelerated by gravitation. There is no any singularity in the whole space- time. When particle is at the original point
. The particle is monotonously accelerated by gravitation. There is no any singularity in the whole space- time. When particle is at the original point , we have
, we have
 (37)
(37)
 (38)
(38)
It indicates that the speed of particle tends to have light’s speed in vacuum at point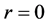 . Acceleration is also finite. So within the region
. Acceleration is also finite. So within the region , the motion of particle with static mass is continuous. Only at point
, the motion of particle with static mass is continuous. Only at point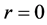 , the force acted on particles becomes infinite. But this kind of singularity appears in any theories in which particles are considered with infinite small size, and have nothing to do with space-time singularity. The singularity of the Schwarzschild solution is eliminated.
, the force acted on particles becomes infinite. But this kind of singularity appears in any theories in which particles are considered with infinite small size, and have nothing to do with space-time singularity. The singularity of the Schwarzschild solution is eliminated.
3. The Fiedmann Equation of Cosmology Needs Relativity Revision
3.1. The Fiedmann Equation is Equivalent to the Newtonian Theory of Gravity
The Fiedmann equation of cosmology is based on the Einstein’s equation of gravity. Because the equation is too complex to solve, two simplified conditions are used. One is the R-W metric and another is the static energy momentum tensor. Using them, we obtain from the Einstein’s equation of gravity
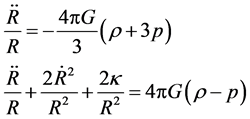 (39)
(39)
Here  is scalar factor,
is scalar factor, 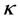 is curvature constant factor,
is curvature constant factor, 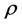 is the universe material density and
is the universe material density and  is the intensity of pressure. By eliminating
is the intensity of pressure. By eliminating 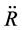 form (39), we obtain the Fiedmann equation
form (39), we obtain the Fiedmann equation
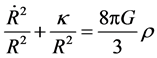 (40)
(40)
Cosmic constant has not been considered in (39) and (40). We often either take it as zero, or combine it with effective material density for convenience.
However, British physicist E. A. Milne proved in 1943 that the Fiedmann equation could be deduced simply based on the Newtonian theory of gravity. Though the Fiedmann equation is described in curved space-time and the Newtonian theory of gravity is described in flat space-time, the results are the same actually when we use them to calculate practical problems, especially when we take curvature constant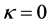 . However, the Newtonian theory of gravity is only suitable for the motions with low speeds. For the high speed expansion of the universe, it is unsuitable. The Fiedmann equation needs relativity revision due to this fact.
. However, the Newtonian theory of gravity is only suitable for the motions with low speeds. For the high speed expansion of the universe, it is unsuitable. The Fiedmann equation needs relativity revision due to this fact.
We now repeat Milne’s deduction below. According to the principle of cosmology, the universe can be considered as a huge sphere with uniform and isotropic material distribution. According to the Newtonian theory, gravity acted on a body located at point r inside the sphere is only related to the mass contained in the sphere with radius r, having nothing to do with the mass outside the sphere. Suppose that the mass of uniform sphere to be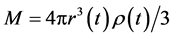 , in the direction of sphere radius, the Newtonian equation of gravity is
, in the direction of sphere radius, the Newtonian equation of gravity is
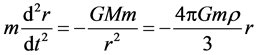 (41)
(41)
For the expansive sphere, by considering co-moving coordinate  in which
in which 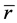 has nothing to do with time, (41) becomes
has nothing to do with time, (41) becomes
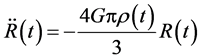 (42)
(42)
(42) is the same as the first formula of (39) when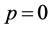 . Because mass is invariable in the expansive pro- cess, we have
. Because mass is invariable in the expansive pro- cess, we have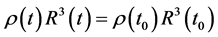 , here
, here 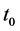 is the time at present. We have
is the time at present. We have
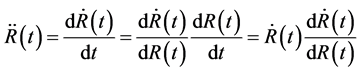 (43)
(43)
Substituting (43) in (42) and taking the integral, we obtain (40). In this case, integral constant 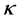 is equivalent with curvature constant in the R-W metric.
is equivalent with curvature constant in the R-W metric.
It is obvious that (40) is the direct result of the Newtonian theory of gravity, for it dose not contain any revised item of relativity. This is why the standard theory of cosmology is effective for same problems, but is ineffective for other problems such as the high red shift of supernova. The reason is that two simplified conditions are used, so that the Freidmann equation becomes non-relativity theory actually. We discuss these problems below.
3.2. The R-W Metric Violates the Principle of Invariance of Light’s Velocity
According to the principle of cosmology, the universe is uniform and isotropy. The R-W metric is considered with the biggest space-time symmetry. Its form is
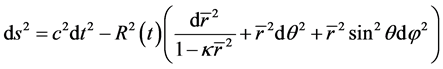 (44)
(44)
In which 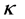 is curvature factor. When
is curvature factor. When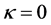 , the me- tric becomes flat with
, the me- tric becomes flat with
 (45)
(45)
For light’s motion, we have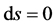 . When light moves along radius direction, we have
. When light moves along radius direction, we have . According to (45), we obtain
. According to (45), we obtain
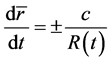 (46)
(46)
For the light’s source fixed at point , coordinate
, coordinate  does not change with time. But for the light emitted by light’s source, coordinate
does not change with time. But for the light emitted by light’s source, coordinate  changes with time as described in (46). The velocity of space expansion is
changes with time as described in (46). The velocity of space expansion is
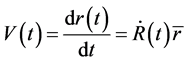 (47)
(47)
By considering (46) and (47), the velocity of light relative to observer located at the original point of reference frame is
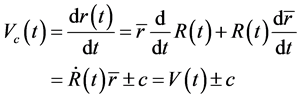 (48)
(48)
The formula indicates that light’s velocity is related to the expansion speed of space and violates the principle of invariance of light’s speed.
In fact, at the moment when light is just emitted out, (48) is the Galileo’s addition rule of light’s velocity. When light moves towards observer, minus sign is taken in (48) so light’s speed is less than its speed in vacuum. When the light moves apart from observer, plus sign is taken. In this case, light’s speed exceeds its speed in vacuum. Especially, because 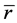 increases with time, enough long time later, light’s speed may greatly exceed its speed in vacuum.
increases with time, enough long time later, light’s speed may greatly exceed its speed in vacuum.
This is not allowed in physics. As we know that the watershed between classical physics and modern physics is just on the invariance principle of light’s speed. Because the R-W metric violates this principle, it can not be used as the space-time frame for modern cosmology which is considered as the theory of relativity. Especially when the expansion speed of the universe is great, huge error will be caused.
As for the curve space with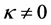 , let
, let  and
and 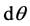
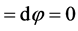 in (44), we obtain
in (44), we obtain

or
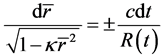 (49)
(49)
On the other hand, as we known that coordinate 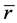 has no meaning of measurement in curved space. What is meaningful is proper distance. Suppose that an observer stays at the original point of coordinate system, the definition of proper distance for the R-W metric between observer and light’s source is [5].
has no meaning of measurement in curved space. What is meaningful is proper distance. Suppose that an observer stays at the original point of coordinate system, the definition of proper distance for the R-W metric between observer and light’s source is [5].
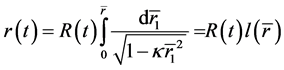 (50)
(50)
Here 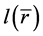 equivalent to
equivalent to 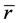 in the flat space. For illuminant material moving in the expansive universe,
in the flat space. For illuminant material moving in the expansive universe,  does not change with time. The velocity of illumi-
does not change with time. The velocity of illumi-
nant material relative to observer is . By
. By
considering (49), the velocity of light emitted by illuminant material moves in the curved space is
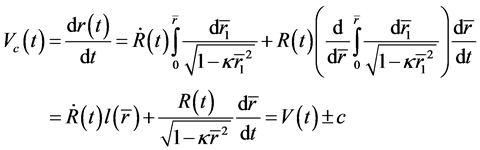 (51)
(51)
So (51) still violates the principle of invariance of light’s speed. In fact, the four dimensional metric of flat space-time is
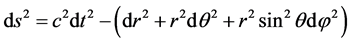 (52)
(52)
by using co-moving coordinate 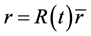 in (52), we obtain
in (52), we obtain
 (53)
(53)
It is completely different from the R-W metric (44) when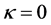 . The metric (53) seems to be curved but is flat essentially. According to the principle of the Riemannian geometry, if we can find a method to turn a curved space into flat, the original space is flat essentially. If we can not find such method, the original space is a curved space in essence. It is obvious that we can not find a transformation to turn (52) into (45) when
. The metric (53) seems to be curved but is flat essentially. According to the principle of the Riemannian geometry, if we can find a method to turn a curved space into flat, the original space is flat essentially. If we can not find such method, the original space is a curved space in essence. It is obvious that we can not find a transformation to turn (52) into (45) when , the spatial part of (45) can not be flat!
, the spatial part of (45) can not be flat!
On the other hand, the four dimensional metric in which three dimensional space has a constant curvature 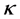 is
is
 (54)
(54)
by using co-moving coordinate in (54), we obtain
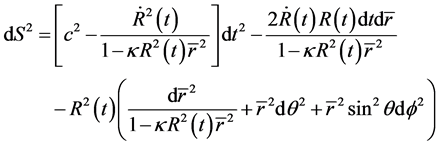 (55)
(55)
Let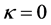 , we reach (53) rather then (45). Therefore, if we use co-moving coordinate to describer the expansive universe in which the space is flat, we should use (53), rather than (45). If we describe the expansive universe with constant curvature, we should use (55), rather than (44).
, we reach (53) rather then (45). Therefore, if we use co-moving coordinate to describer the expansive universe in which the space is flat, we should use (53), rather than (45). If we describe the expansive universe with constant curvature, we should use (55), rather than (44).
Another result of using the R-W metric in cosmology is that it leads to the united universe time. In the R-W metric,  indicates that we have the same time for any spatial point in the expansive universe. This obviously violates special relativity. Because there is a relative motion speed between two objects in the expansive universe, there exists time delay between them according to special relativity. It is actually the result of the Newtonian mechanics to use the united universe time in cosmology. This is another reason why we say that the Friedmann equation is equivalent to the Newtonian mechanics.
indicates that we have the same time for any spatial point in the expansive universe. This obviously violates special relativity. Because there is a relative motion speed between two objects in the expansive universe, there exists time delay between them according to special relativity. It is actually the result of the Newtonian mechanics to use the united universe time in cosmology. This is another reason why we say that the Friedmann equation is equivalent to the Newtonian mechanics.
However, it is easy to prove that if we use flat space- time metric (53) in the Einstein’s equation of gravity, the Einstein’s tensor would become zero with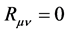 . In this way, we can not describe the gravity field of the expansive universe. Therefore, both the R-W metric and the flat space-time metric are unsuitable for cosmology. We should look for other proper methods to describe the expansive universe.
. In this way, we can not describe the gravity field of the expansive universe. Therefore, both the R-W metric and the flat space-time metric are unsuitable for cosmology. We should look for other proper methods to describe the expansive universe.
3.3. Dynamic Energy Momentum Tensor Should Be Used in Cosmology
The energy momentum tensor of ideal liquid is used in cosmology with the form
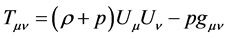 (56)
(56)
Here 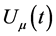 is the four dimensional velocity. In the standard cosmology, we take
is the four dimensional velocity. In the standard cosmology, we take 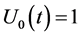 and
and 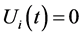 with
with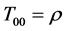 ,
,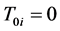 . It means that we take static energy momentum tensor energy in the Einstein’s equation of gravity without considering material’s velocity.
. It means that we take static energy momentum tensor energy in the Einstein’s equation of gravity without considering material’s velocity.
This is an excessively simplified approximation. In fact, there exist relative velocities between materials and observers in the expansive universe. The most basic fact for cosmology is the Hubble’s red shift, which is explained as the kinematical effect caused by relative velocities be- tween observer and luminous material. If co-moving co- ordinate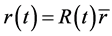 , material’s speed is
, material’s speed is 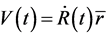
 . In fact, on the left side of the Fiedmann equation, we have
. In fact, on the left side of the Fiedmann equation, we have . How can we take
. How can we take 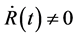 on the right side of equation which contains energy momentum tensor? It is absolutely unjustifiable to use static energy momentum tensor to describe the expansive universe. In fact, if we use static energy momentum tensor to describe the expansive universe, what do we use to describer the static universe? This is a problem to make us embarrassing.
on the right side of equation which contains energy momentum tensor? It is absolutely unjustifiable to use static energy momentum tensor to describe the expansive universe. In fact, if we use static energy momentum tensor to describe the expansive universe, what do we use to describer the static universe? This is a problem to make us embarrassing.
According general relativity, we can use arbitrary reference frame to describe the gravity field. By using common spherical coordinate system, the partial velocities of an object which moves along the radius direction are 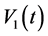
 ,
,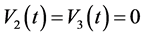 . The forth dimensional velocities are (
. The forth dimensional velocities are ( ).
).
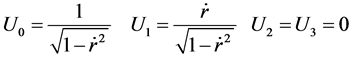 (57)
(57)
To simplify discussion below, we use the R-W metric and take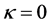 . For the expansive universe with uniform distribution of material, dynamic energy momentum tensors are
. For the expansive universe with uniform distribution of material, dynamic energy momentum tensors are
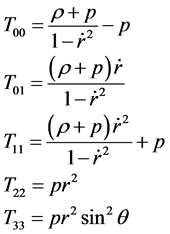 (58)
(58)
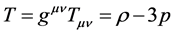 (59)
(59)
Substituting them in the Einstein’s equation of gravity
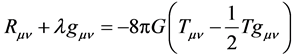 (60)
(60)
We get the motion equations of cosmology
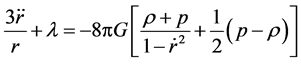 (61)
(61)
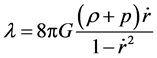 (62)
(62)
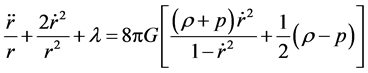 (63)
(63)
Substitute 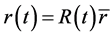 in the formulas, we get
in the formulas, we get
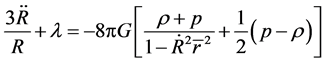 (64)
(64)
 (65)
(65)
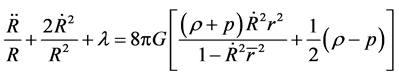 (66)
(66)
Take 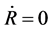 on the right sides but not on the left sides, we obtain the Fiedmann equation. But we can not do it in this way. Because
on the right sides but not on the left sides, we obtain the Fiedmann equation. But we can not do it in this way. Because 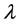 is a constant, we have three ways to make (65) tenable. The first is to let
is a constant, we have three ways to make (65) tenable. The first is to let 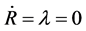 which describes the static universe. By considering the observation fact of the Hubble redshift, this is improper. The second is to take simultaneously
which describes the static universe. By considering the observation fact of the Hubble redshift, this is improper. The second is to take simultaneously
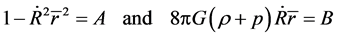 (67)
(67)
Here A and B are constants. From (67), we obtain
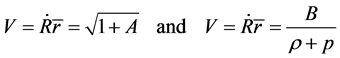 (68)
(68)
The result violates the Hubble law too. In addition, these velocities are inconsistent, so (68) is impossible. The third is to get the solution from (65)
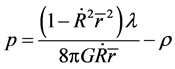 (69)
(69)
Substitute (69) in (64) and (66), we have
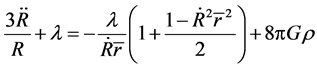 (70)
(70)
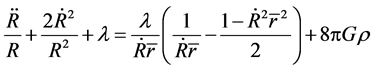 (71)
(71)
by cancelling 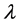 from two formulas above, we obtain at last
from two formulas above, we obtain at last
 (72)
(72)
The equation becomes so complicated that it is impossible to solve actually. On the other hand, because the right hand sides of (64)-(66) contain , if
, if 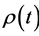 and
and 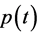 are still unrelated to
are still unrelated to , we should have
, we should have 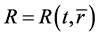 by solving the equations. The result contradicts with the origi- nal definition
by solving the equations. The result contradicts with the origi- nal definition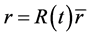 . In order to mate
. In order to mate 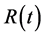 unrelated to
unrelated to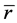 ,
, 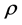 and
and 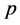 should be related to
should be related to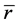 . In this
. In this
way, the principle of cosmology can not hold again. The result means that we will be in dilemma if dynamic energy momentum tensor is used in cosmology.
Pioneers of cosmology must have considered this problem, so they had to use static energy momentum to establish the equation of cosmology. In the early stage of cosmology, the observed expansion speed of the universe was low, so the simplified motion equation could be suitable. When cosmology develops to now day’s level, we observe cosmic phenomena which take place in the high speed expansive processes such as the high red shift of supernova. The simplified Friedmann equation becomes unsuitable so that many difficulties appear in the standard cosmology at present. This is the main reason why we have to introduce the hypothesis of the accelerating expansion of the universe, dark energy and non-baryon dark material.
4. Velocity, Acceleration and Initial Conditions of the Universe Expansion
4.1. Velocity and Acceleration of the Universe Expansion
Because (72) can not be solved practically when dynamic energy momentum tensor is considered, we have to look for other method to describe the expansive universe. We prove below that based on the revised formula (25), the high red shift of supernova can be explained well. There- fore, we do not need the hypothesis of dark energy and the universe accelerating expansion again.
In principle, we can take the CMB as static reference to describe the universe expansion. Practically, we take the earth as static reference frame for convenience. Suppose that the universe material is distributed with spherical symmetry and uniform density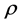 . The static mass of sphere with radius R is
. The static mass of sphere with radius R is . Similarly we have
. Similarly we have 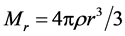 with radius r. According to the Newtonian theory, gravity acted on a small object located at point r with mass
with radius r. According to the Newtonian theory, gravity acted on a small object located at point r with mass 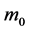 is [6]
is [6]
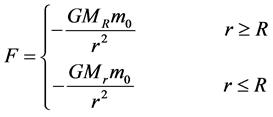 (73)
(73)
The formulas indicate that when mass  is located outsider the sphere with
is located outsider the sphere with , the gravity acted on it is equal to that when the spherical mass is centralized at the center of sphere. When mass
, the gravity acted on it is equal to that when the spherical mass is centralized at the center of sphere. When mass 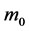 is located inside the sphere with
is located inside the sphere with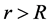 , the gravity acted on it is only related to
, the gravity acted on it is only related to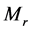 , having nothing to do with the mass distributed outside the radius r.
, having nothing to do with the mass distributed outside the radius r.
Suppose that the universe expands along the direction of radius. In the process, angle momentum L is equal to zero. We calculate gravity between a spherical shell with radius R and an object located at point 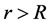 with static mass
with static mass  and speed
and speed  along radius direction. Suppose that
along radius direction. Suppose that  satisfies (22) approximately, we use (22) to describe object’s effective mass. According to (23) and (25), we have
satisfies (22) approximately, we use (22) to describe object’s effective mass. According to (23) and (25), we have
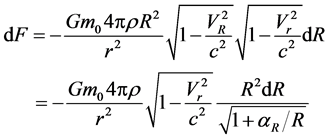 (74)
(74)
Here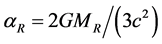 . Let
. Let ,
,
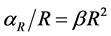 , and taking the integral of (74), we get the total gravity that the expansive sphere with radius
, and taking the integral of (74), we get the total gravity that the expansive sphere with radius  acts on an object located on the spherical surface with static mass
acts on an object located on the spherical surface with static mass 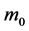 and speed
and speed 
 (75)
(75)
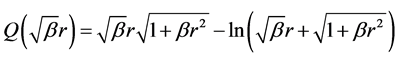 (76)
(76)
On the other hand, according to special relativity, we have
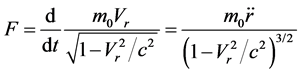 (77)
(77)
Based on (76) and (77), we get the acceleration of an object located on spherical surface
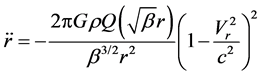 (78)
(78)
The acceleration is just related to the mass inside the sphere, and unrelated to the mass outsider the sphere. We also consider (78) as the expansion speed of spherical surface with radius r. Let 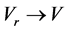 and using relation
and using relation 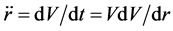 in (78), we obtain
in (78), we obtain
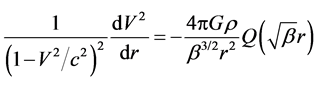 (79)
(79)
Let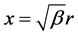 , we have
, we have
 (80)
(80)
In the expansion process of the universe, 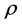 changes while spherical radius r changes. But spherical mass M is
changes while spherical radius r changes. But spherical mass M is
unchanged with 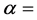 constant. We have
constant. We have 
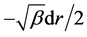 or
or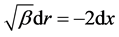 . Suppose that initial radius
. Suppose that initial radius
is 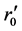 (
(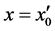 ) and initial speed is
) and initial speed is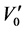 , substituting the relation into (79) and take the integral. Let
, substituting the relation into (79) and take the integral. Let
 (81)
(81)
we get
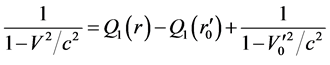 (82)
(82)
Let
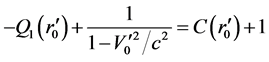 (83)
(83)
we have
 (84)
(84)
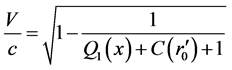 (85)
(85)
Because (81) can not be integrated directly, we need approximate method. When x is very small (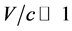 ), by developing (76) into the Taylor’s series in the region of
), by developing (76) into the Taylor’s series in the region of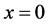 , we obtain
, we obtain
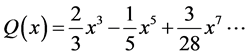 (86)
(86)
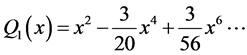 (87)
(87)
By considering (80), (87) becomes
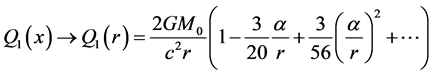 (88)
(88)
Substituting the formulas in (78) and (85), we obtain the formula of acceleration and speed of the universe expansion
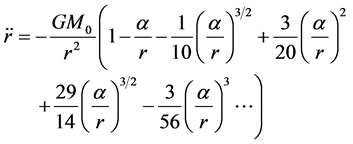 (89)
(89)
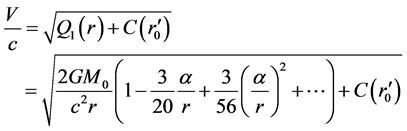 (90)
(90)
4.2. Initial Condition of the Universe Expansion
In the discussion above, we assume that material is only acted by gravity. However, practical situation is that strong, weak and electromagnetic interactions could not be neglected in the early phase of the universe during which material density was great. Even more, some unknown interaction may exist.
According to the theory of Einstein’s theory, material may be compressed into infinite density by gravity. How- ever, infinite density is unimaginable. In fact, the author had proved that due to use the improper boundary condition of flat space-time in the gravity theory of curved space-time, the current theory of singularity black hole is wrong. By strict calculation based on the Einstein’s equation of gravity and curved boundary condition, singular black hole with infinity density do not exist [7,8]. By the same reasons, the fashionable idea that the universe originated from infinite small point is also impossible.
In order to avoid infinite density, we assume that there exist a certain mechanism so that material sphere with mass M can only be compressed to a finite radius r0. In this way, the motion equation of the universe expansion should be revised as
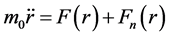 (91)
(91)
Here 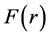 is gravity and
is gravity and 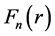 is the sum of other forces. For convenience, we simplify
is the sum of other forces. For convenience, we simplify
 (92)
(92)
Here  is undetermined function. It corresponds to an infinite potential barrier with radius r0 on which the spherical surface can not be contracted further. Meanwhile, by the action of
is undetermined function. It corresponds to an infinite potential barrier with radius r0 on which the spherical surface can not be contracted further. Meanwhile, by the action of  at the spherical surface with radius
at the spherical surface with radius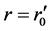 , the process of contraction become expansion and the surface moves with a positive acceleration. When
, the process of contraction become expansion and the surface moves with a positive acceleration. When , other forces become zero and only gravity acts. When
, other forces become zero and only gravity acts. When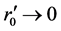 , it is just the so-called big bang of the universe from an infinite singular point. By considering (92), (79) becomes
, it is just the so-called big bang of the universe from an infinite singular point. By considering (92), (79) becomes
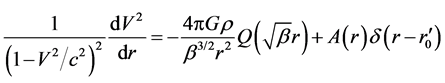 (93)
(93)
The integral of (93) is
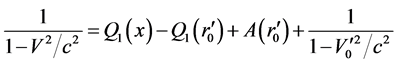 (94)
(94)
Let
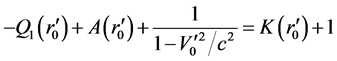 (95)
(95)
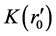 represents the initial condition of the universe expansion. For different objects located at different position r now days, their initial positions
represents the initial condition of the universe expansion. For different objects located at different position r now days, their initial positions 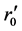 and
and 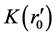 are different. We will discuss how to decide
are different. We will discuss how to decide 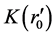 later. In this way, (94) becomes
later. In this way, (94) becomes
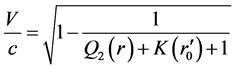 (96)
(96)
Under the condition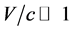 , by considering (86) and (88), the formulas of velocity and acceleration can be written as
, by considering (86) and (88), the formulas of velocity and acceleration can be written as
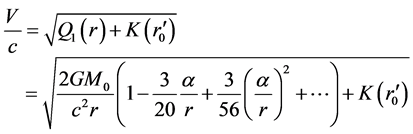 (97)
(97)
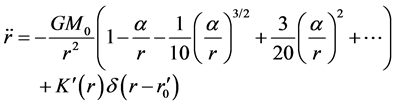 (98)
(98)
Here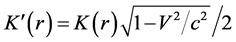 . If expansive velocity is great, we should use (78) and (96) directly.
. If expansive velocity is great, we should use (78) and (96) directly.
5. Red Shifts of Cosmology and Hubble Diagram of Supernova
5.1. Red Shift of Cosmology
According to the Doppler’s formula, when celestial body moves along radius direction, we have relation between speed and red shift
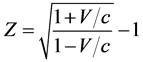 (99)
(99)
Suppose that observer is located at the origin point of flat reference frame, the distance between observer and celestial body is 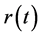 at moment
at moment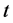 . In the expanding process of the universe, celestial body moves from
. In the expanding process of the universe, celestial body moves from 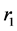 to
to 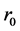 with
with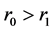 , while the light travels from
, while the light travels from 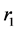 to observer along opposite direction. Suppose light’s speed is invariable in the process, we have following relation
to observer along opposite direction. Suppose light’s speed is invariable in the process, we have following relation
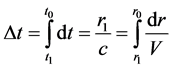 (100)
(100)
According to (96), we have
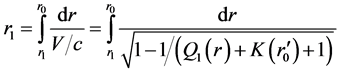 (101)
(101)
The real distance between observer and celestial body is 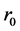 at present moment
at present moment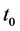 . We know the universe material density
. We know the universe material density 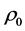 at time
at time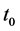 , but do not know its value
, but do not know its value 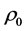 at arbitrary time t. By considering relation
at arbitrary time t. By considering relation 
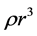 , we write (80) as
, we write (80) as
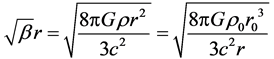 (102)
(102)
Using (102) in (101) and taking the integral, we can obtain the relation in principle
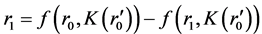 (103)
(103)
In the formulas above, 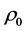 ,
, 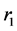 and Z are known through observations, but
and Z are known through observations, but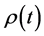 ,
, 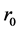 and
and 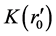 are unknown. By the relation
are unknown. By the relation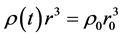 , we can determinate
, we can determinate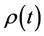 . By
. By
connecting (100) and (103), we can determinate 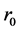 and
and . (101) can only be calculated by numerical method through computer. By taking G = 6.67 × 10?11, r0 = y0 × 1026 m, r1 = y1 × 1026 m and
. (101) can only be calculated by numerical method through computer. By taking G = 6.67 × 10?11, r0 = y0 × 1026 m, r1 = y1 × 1026 m and 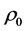 = b× 10?26 kg/m3, we have
= b× 10?26 kg/m3, we have
 (104)
(104)
We use x as basic variable to calculate y0 and 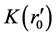 in which b, Z and y1 are input parameters. According to this paper, we actually deduce the initial situations of the universe expansion reversely based on the present observations of red shift and distances. In other words, as long as the initial conditions of the universe expansion are known, we can know its current situations.
in which b, Z and y1 are input parameters. According to this paper, we actually deduce the initial situations of the universe expansion reversely based on the present observations of red shift and distances. In other words, as long as the initial conditions of the universe expansion are known, we can know its current situations.
5.2. The Red Shift of Ia Supernova
In Figure 1, the curved line with  and
and 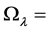
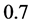 represents practical relation between red shift and distance of Ia supernova at the early period of time t. According to photometry measurement, the density of luminous material in the universe is about
represents practical relation between red shift and distance of Ia supernova at the early period of time t. According to photometry measurement, the density of luminous material in the universe is about 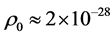 kg/m3 at present day. Because there exist a great mount of non-luminous material, we suppose that practical material is 10 times more than luminous material and let
kg/m3 at present day. Because there exist a great mount of non-luminous material, we suppose that practical material is 10 times more than luminous material and let  kg/m3. In Figure 1, we take
kg/m3. In Figure 1, we take 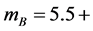
 in which
in which  is luminosity distance with unit length
is luminosity distance with unit length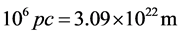 . But the concept of luminosity distance is unnecessary in this paper for our discussion is based on flat space-time. So we need to transform
. But the concept of luminosity distance is unnecessary in this paper for our discussion is based on flat space-time. So we need to transform 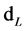 to real distance r.
to real distance r.
The curved line in Figure 2 shows the relations between red-shifts, distances and parameters of initial condition of Ia supernova. The vertical coordinate is the values of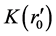 . The bottom horizontal coordinate is the value of red-shift. On the upside, under the line of horizontal coordinate are the values of distance r, above the line is the values of r0. For Z = 1 and
. The bottom horizontal coordinate is the value of red-shift. On the upside, under the line of horizontal coordinate are the values of distance r, above the line is the values of r0. For Z = 1 and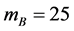 , we get
, we get . By the numerical calculation, we obtain
. By the numerical calculation, we obtain 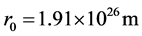 and
and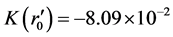 . For Z = 0.5 and
. For Z = 0.5 and 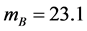 corresponding to r1 = 0.67 × 1026 m, we obtain
corresponding to r1 = 0.67 × 1026 m, we obtain 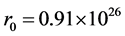 and
and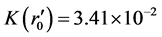 . For Z = 0.1 and
. For Z = 0.1 and  corresponding to r1 = 0.15 × 1026 m, we obtain r = 0.16 × 1026 and
corresponding to r1 = 0.15 × 1026 m, we obtain r = 0.16 × 1026 and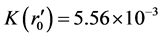 .
.
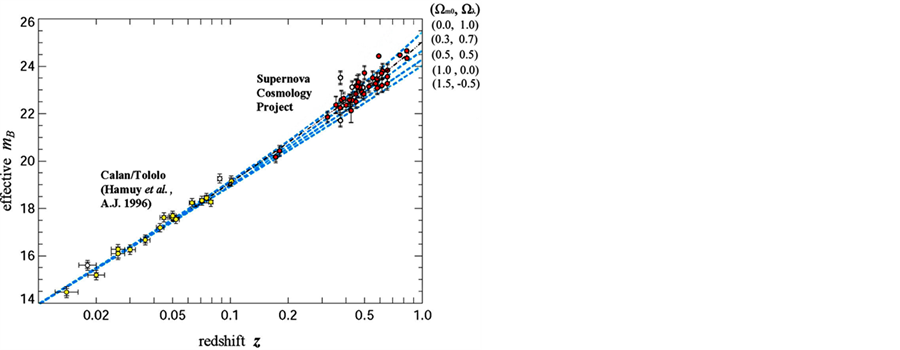
Figure 1. Hubble diagram for red shift and distance of Ia supernova (Cited from Ricss A.G. et al., 1998).
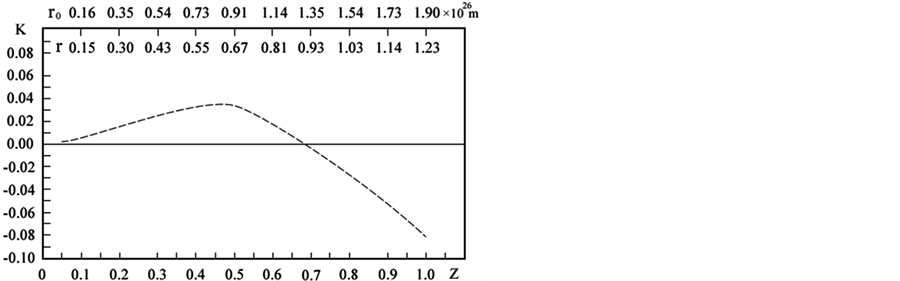
Figure 2. Relations between red-shifts, distances and initial parameters of Ia supernova.
In this way, we can explain the high red shift of Ia supernova well. The hypotheses of dark energy and the accelerating expansion of the universe become unnecessary. The universe began its expansion from a finite volume, rather than from a singularity.
6. Revised Equation of Cosmology
In order to compare with the equations of cosmology, we now transform (97) and (98) to the form of the Friedmann equation. Suppose that the universe is a uniform
sphere with density . We define
. We define  in which
in which 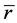 is a parameter unrelated with time. Let
is a parameter unrelated with time. Let 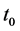 represent today’s time, we have
represent today’s time, we have 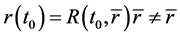 and can write (80) as
and can write (80) as
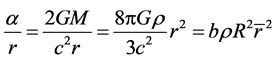 (105)
(105)
Here . Under the condition
. Under the condition , (100) can be written as
, (100) can be written as
 (106)
(106)
Similarly, let , we can write (97) as
, we can write (97) as
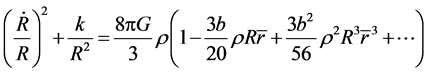 (107)
(107)
On the other hand, the Friedmann equation containing cosmic constant  are
are
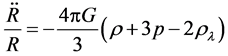 (108)
(108)
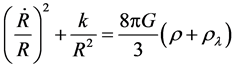 (109)
(109)
Here 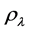 is considered as a constant energy density corresponding to vacuum and
is considered as a constant energy density corresponding to vacuum and  in the current cosmology. Comparing (106) and (107) with (108) and (109), we have
in the current cosmology. Comparing (106) and (107) with (108) and (109), we have
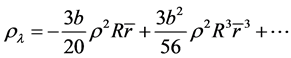 (110)
(110)
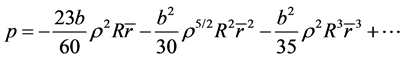 (111)
(111)
It is obvious that after (110) and (111) are used, revised equations in this paper are with the same form with the Freidmann equation. The differences are that  is not a constant,
is not a constant, 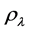 and p are also related to
and p are also related to . In order to be consistent with the observation of Ia supernova’s red shift, the current theory have to assume
. In order to be consistent with the observation of Ia supernova’s red shift, the current theory have to assume 
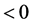 , so that we have to think that the universe is pushed by repulsive force and do accelerating expansion. According to this paper, we always have
, so that we have to think that the universe is pushed by repulsive force and do accelerating expansion. According to this paper, we always have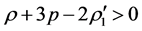 , so there is no repulsive force and accelerating expansion again. Because the forms of differential equations (106) and (107) are very complex, it is more convenience for us to use (97) and (98) directly to do calculations.
, so there is no repulsive force and accelerating expansion again. Because the forms of differential equations (106) and (107) are very complex, it is more convenience for us to use (97) and (98) directly to do calculations.
7. The Hubble Constant, Dark Material and the Universe Age
7.1. The Hubble Constant
According to (97), we have
 (112)
(112)
Let 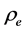 represent the equivalent density of the universe
represent the equivalent density of the universe
 (113)
(113)
We get
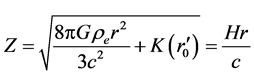 (114)
(114)
At present 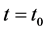 and
and , the Hubble constant is
, the Hubble constant is
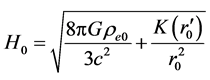 (115)
(115)
We see that 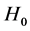 is related to
is related to  and
and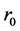 , not a real constant even under condition
, not a real constant even under condition . This is the reason why we can not determinate the Hubble constant precisely up to present days.
. This is the reason why we can not determinate the Hubble constant precisely up to present days.
In fact, only taking the first and last items in (98), we obtain the result of the Newtonian theory
 (116)
(116)
Taking 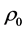 = 2× 10?26 kg/m3 and
= 2× 10?26 kg/m3 and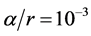 , we get
, we get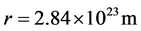 . In cosmology, we generally take
. In cosmology, we generally take 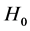
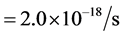
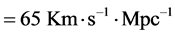 . We get
. We get 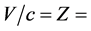
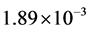 and
and 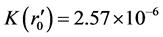 according to (116). In the calculation, we consider r as the present position of luminous celestial, without considering its practical position to be r0. For the situation with Z = 1 and
according to (116). In the calculation, we consider r as the present position of luminous celestial, without considering its practical position to be r0. For the situation with Z = 1 and 
 , according to (116), the result is
, according to (116), the result is 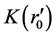
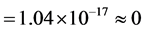 . The result indicates that even though based on the Newtonian theory of gravity, we can also explain the high red shift of the Ia Supernova by taking different
. The result indicates that even though based on the Newtonian theory of gravity, we can also explain the high red shift of the Ia Supernova by taking different 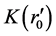 for different objects. It is also unnecessary for us to introduce the concept of dark energy by introducing the effect of initial conditions.
for different objects. It is also unnecessary for us to introduce the concept of dark energy by introducing the effect of initial conditions.
For 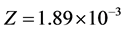 and
and , by using (96) for accurate numerical calculation, the result is
, by using (96) for accurate numerical calculation, the result is 
 and
and  which is similar to that based on (116). But for the situations of high red shift, the differences of results are large.
which is similar to that based on (116). But for the situations of high red shift, the differences of results are large.
7.2. Non-Baryon Dark Material
According to the theory of nuclei synthesis in cosmology, relative density of baryon is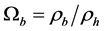 , in which
, in which 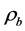 is baryon’s density and
is baryon’s density and 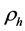 is total density of all material. We have relation [9]
is total density of all material. We have relation [9]
 (117)
(117)
Take 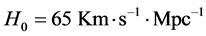 which corresponds to
which corresponds to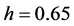 , we have
, we have  = 7.9× 10?27 kg/m3 and
= 7.9× 10?27 kg/m3 and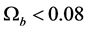 . Practical observation is
. Practical observation is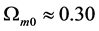 , so the theory indicates that our universe is mainly composed of non- baryon material. However, according to this paper, by considering the existence of parameter
, so the theory indicates that our universe is mainly composed of non- baryon material. However, according to this paper, by considering the existence of parameter in (115), it is enough for us to take
in (115), it is enough for us to take 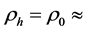 2 × 10?27 kg/m3 and get
2 × 10?27 kg/m3 and get 
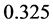 and
and . We do not need the hypothesis of non-baryon dark material. At least, we do not need to assume that non-baryon dark material is 5 ~ 6 times more than normal baryon material in the universe if non-baryon dark material exists actually.
. We do not need the hypothesis of non-baryon dark material. At least, we do not need to assume that non-baryon dark material is 5 ~ 6 times more than normal baryon material in the universe if non-baryon dark material exists actually.
7.3. The Age of the Universe
We consider the universe as a material sphere with radius  at initial moment, which is about the distance between the sun and the earth. Long enough later, an observer located at the original point of reference frame receives the light omitted from a celestial body on the spherical surface with radius
at initial moment, which is about the distance between the sun and the earth. Long enough later, an observer located at the original point of reference frame receives the light omitted from a celestial body on the spherical surface with radius 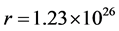 kg/m3 and find its red shift is
kg/m3 and find its red shift is 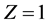 at time
at time . Suppose that the material density of the universe is
. Suppose that the material density of the universe is  at present, the initial density inside the sphere is
at present, the initial density inside the sphere is  kg/m3, equal to the density of neutron star. According to the calculation before, the celestial body has moved to the position
kg/m3, equal to the density of neutron star. According to the calculation before, the celestial body has moved to the position  m at present moment. We consider this distance as the radius of the observable universe and substitute corresponding value
m at present moment. We consider this distance as the radius of the observable universe and substitute corresponding value  to following formula to calculate the time during which the universe expands from radius
to following formula to calculate the time during which the universe expands from radius  m to
m to 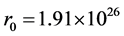 m.
m.
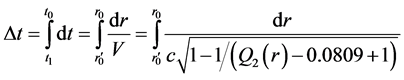 (118)
(118)
The result is 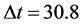 billion years. But this value is not sensitive to small initial radius. Taking
billion years. But this value is not sensitive to small initial radius. Taking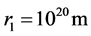 , equal to the radius of the Milky Way galaxy, the result is the almost same. It means that the age of the universe mainly depends on the later expansive process.
, equal to the radius of the Milky Way galaxy, the result is the almost same. It means that the age of the universe mainly depends on the later expansive process.
Using (118) to calculates the time during which the universe radius expanses from 1.23 × 1026 m to 1.95 × 1026 m, the result is 13 billion years, so the time during which the radius of the universe expanses from 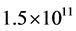 m to 1.23 × 1026 m is 17.8 billion years. This is just the universe age we consider at present. In the present cosmology, the universe age is estimated to be about 10 ~ 15 billion years, too short to the formation of galaxies [10]. The problem does not exist according to this paper.
m to 1.23 × 1026 m is 17.8 billion years. This is just the universe age we consider at present. In the present cosmology, the universe age is estimated to be about 10 ~ 15 billion years, too short to the formation of galaxies [10]. The problem does not exist according to this paper.
8. Conclusions
By transforming the geodesic equation of the Schwarzs- child solution of the Einstein’s equation into flat space- time to describe, the revised Newtonian formula of gravity and the revised equation of cosmology are obtained. The singularity problem in the Einstein’s theory of gravity described in curved space-time is eliminated thoroughly.
Because using two improper and approximate conditions, the Freidmann equation becomes the result of the Newtonian theory of gravity actually. It is only suitable to describe the low speed expansive processes of the universe, unsuitable to describe the high speed expansion. The equation of cosmology needs relativity revision.
By using the revised Newtonian formula of gravity, the revised equation of cosmology is obtained. The high red-shift of supernova can be well explained. It is unnecessary for us to introduce the hypotheses of the universe accelerating expansion and dark energy. It is also unnecessary for us to assume that non-baryon dark material is 5 - 6 times more than normal baryon dark material if it exists actually. Many problems existing in cosmology including the problem of the universe age can be resolved well.
In this way, the theory of gravity returns to the traditional form of dynamic description and becomes normal one. The revised equation can be used as the foundation of more rational cosmology.
References
- 1. N. Rosen, “General Relativity and Flat Space,” Physical Review, Vol. 57, No. 2, 1940, pp. 147-150. doi:10.1103/PhysRev.57.147
- 2. Y. J. Wang and Z. M. Tang, “Theory and Effects of Gravitation,” Hunan Science and Technology Publishing Company, 1990, pp. 547-589.
- 3. X. C. Mei, “The R-W Metric Has No Constant Curvature When Scalar Factor R(t) Changes with Time,” International Journal of Astronomy and Astrophysics, Vol. 1, No. 4, 2011, pp. 177-182. doi:10.4236/ijaa.2011.14023
- 4. E. A. Milne, “A Newtonian Expanding Universe,” General Relativity and Gravitation, Vol. 32, No. 9, 2000, pp. 1939-1948. doi:10.1023/A:1001997000979
- 5. S. Weiberge, “Gravitation and Cosmology,” John Wiley and Sons, Inc., New York, 1984, pp. 608.
- 6. C. Kittel, W. D. Knight and M. A. Ruderman, “Mechanics,” Berkeley Physics Course, Vol. 1, 1973, McGraw- Hill, New York.
- 7. X. C. Mei, “The Precise Inner Solutions of Gravity Field Equations of Hollow and Solid Spheres and the Theorem of Singularity,” International Journal of Astronomy and Astrophysics, Vol. 1, No. 3, 2011, pp. 109-116. doi:10.4236/ijaa.2011.13016
- 8. X. C. Mei, “Singularities of the Gravitational Fields of Static Thin Loop and Double Spheres,” Journal of Cosmology, Vol. 13, No. 27, 2011.
- 9. Y. Q. Yu, “Physical Cosmology,” Beijing University Publishing Company, Beijing, 2002, pp. 104, 184.
- 10. M. Bolte and C. J. Hogan, “Conflict Over the Age of the Universe,” Nature, 1995, Vol. 376, pp. 399-402. doi:10.1038/376399a0

