World Journal of Nano Science and Engineering
Vol.05 No.04(2015), Article ID:61074,11 pages
10.4236/wjnse.2015.54014
In the Heart of Femtosecond Laser Induced Nanogratings: From Porous Nanoplanes to Form Birefringence
R. Desmarchelier, B. Poumellec, F. Brisset, S. Mazerat, M. Lancry
ICMMO, UMR CNRS-UPSud 8182, Université Paris Sud (in Université Paris Saclay), Orsay, France

Copyright © 2015 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).


Received 23 July 2015; accepted 10 November 2015; published 13 November 2015

ABSTRACT
It is demonstrated that the form birefringence related to the so-called nanogratings is quantitatively correlated to the porosity-filling factor of these nanostructures. We reveal that matters surrounding the nanopores exhibit significant refractive index decrease which is likely due to the fictive temperature increase and/or the presence of a significant amount of interstitial O2. The control of the porosity was achieved by adjusting the laser pulse energy and the number of pulses/micron i.e. the overlapping rate. Applications can be numerous in fast material processing by the production of nanoporous matter, and photonics by changing the optical properties.
Keywords:
Silica, Glasses, Nanoporous, Femtosecond Laser Processing, Birefringence, Nanogratings

1. Introduction
One of the main advantages of using femtosecond pulses to induce 3D refractive index changes is that energy can be rapidly deposited before thermal build-up which can occur. This restricts thermal spreading so simple, the relaxation kinetics associated with quenched glass do not easily explain changes beyond the damage region when low repetition rate lasers are used. These attributes allow compact 2-D and 3-D multi-component photonic devices [1] -[4] to be fabricated in a single step within a wide variety of transparent materials [5] . For many applications, silica glasses are the preferred material, providing excellent physical and chemical properties such as optical transparency from IR to UV, a low thermal expansion coefficient, long term stability and a high resistance to laser induced damage.
Depending on the pulse parameters, we may define a variety of different laser-material regimes. Typically, the key parameters that can be tuned are the laser repetition rate, the pulse energy and the polarization, with the laser pulse duration and wavelength usually being fixed [6] . In terms of repetition rate, two regimes are categorized: (1) the low repetition rate regime where the material changes are caused by individual pulses [7] ; and (2) the high repetition rate regime where changes arise due to cumulative thermal effects [8] since the time between each pulse is less than the thermal diffusion time of silica. In silica, the border between these regimes occurs around a repetition rate of 1 MHz although this is not easily defined since the thermal dissipation depends on volume and surface area. The investigations of this paper will focus in the low repetition rate regime. Depending on the exposure parameters, three qualitatively different types of structural changes can be induced in fused silica as recently review in [6] : (1) an isotropic positive refractive index change (type-I); (2) a form birefringence with negative index change [9] (type-II); and (3) voids (type-III). Type-I modifications occur above an energy of ~ 0.1 μJ (λ = 800 nm, Δtp = 160 fs, 200 kHz and NA = 0.5) where the index change is permanent and isotropic with a slight stress birefringence [10] [11] . The maximum index change is Δn ~ (3 - 6) × 10−3 in fused silica [7] which is relatively large when compared with the index change achievable with nanosecond lasers [12] [13] .
In contrast, Type-II modifications are significantly different and happen above a higher energy threshold of 0.31 μJ (λ = 800 nm, Δtp = 160 fs, 200 kHz and NA = 0.5) [11] . The index change can be as large as Δn ~ −2 × 10−2 [14] and exhibits impressive thermal durability, exhibiting no signs of decay after two hours at 1000˚C [15] . The most striking features of type-II modifications are that the index change is highly anisotropic. The origins of this anisotropy lie in the formation of sub-wavelength features of the so-called “nanogratings” or “nanoplanes” [16] . The nanoplanes are oriented perpendicular to the direction of /2n but it is the laser polarization. Their spacing is found to be dependent significantly on the pulse energy, and the number of laser pulses [17] . Recently, we have shown that these nanoplanes consisted of porous matter most likely produce as a result of decomposition of SiO2 into SiO2(1-x) + x∙O2 under the intense plasma generation [18] [19] . The formation of nanoporous silica likely explains the refractive index contrast of these nanostructures and thus the observed form birefringence. In this paper, we investigate in details the form birefringence model and the related porous nanoplanes produced by the interaction of the femtosecond laser with silica glass. We reveal that the so-called nanogratings and porous nanoplanes are correlated and we study their changes with both the pulse energy and the pulse-to-pulse overlap.
2. Experimental Details
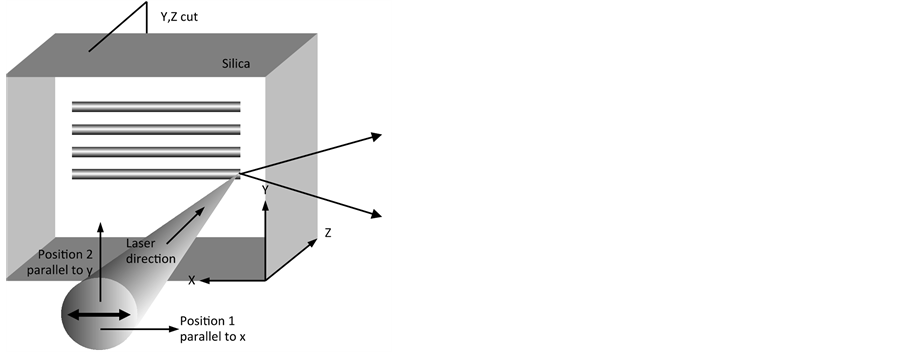
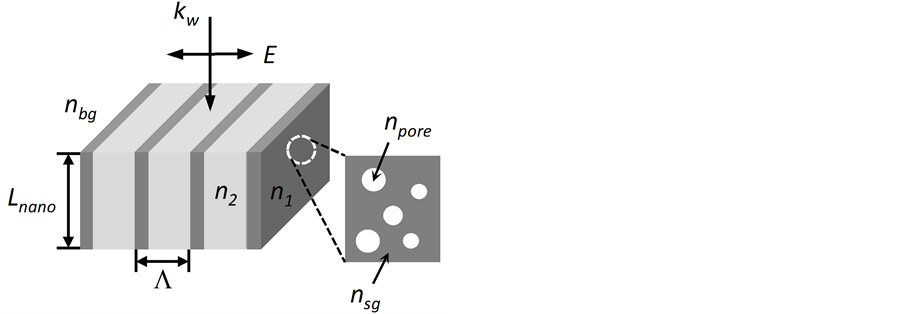
The direct writing procedure using infrared femtosecond laser pulses has been already described extensively in other work [10] [20] and is reminded in Figure 1. In this work, Ge-doped (12 w% in GeO2) silica glass plates of 1 mm thickness and a refractive index equal to 1.4722 at 550 nm are used. Processing is undertaken with a femtosecond fibre laser (λ = 1030 nm, Δtp = 300 fs). The single mode output is focused below the surface of the silica plate using a 0.6 NA aspheric lens with the k vector of the beam being perpendicular to the surface of the plate. The sample can then be moved in three dimensions using computer-controlled stages. The linear polarization of the laser output was
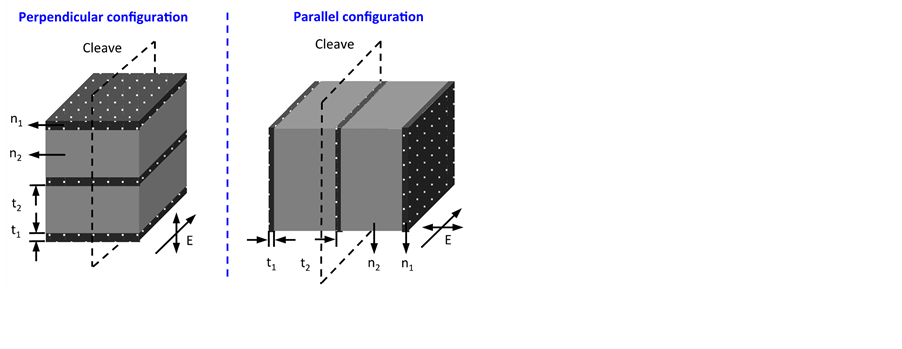
Figure 1. Experimental setup scheme for configuration for writing (from the left side) and schematic of sub- wavelength periodic structure formed in cross-section of the irradiated region. n1 et n2: local refractive indices of the nanoplates; t1 and t2, are their respective thicknesses.
usually kept parallel to the sample translation direction (parallel configuration) although the polarization transverse configuration state was also explored. The laser pulse energy was varied over (0.05 ? 1) μJ; i.e. above the second damage threshold where nanostructures are formed. The scanning speed was varied from 10 up to 1000 μm/s and the repetition rate from 10 kHz up to 500 kHz. This allows varying the pulse-to-pulse overlapping rate from 1 up to 2 × 105 pulses/μm. After irradiation, QPm (Quantitative Phase Microscopy) and quantitative birefringence measurements were performed. The birefringence measurement is based on a Sénarmont compensator that couples a highly precise quarter waveplate with a 180-degree rotating analyzer to provide retardation measurements having an accuracy that approaches λ/100. The device is utilized for retardation measurements over one wavelength range (up to 551.5 nm) for the quantitative analysis of birefringence. Then in order to observe the intimate structure of the nanoplanes, it has been decided to use an original approach. The samples were cleaved using a diamond pen as described in the right side of Figure 1. The laser tracks have been observed using a Field-Emission Gun Scanning Electron Microscope (FEG-SEM, ZEISS SUPRA 55 VP). This allows to examine uncoated dielectric specimens using low accelerating voltage (typ. in the range of 1 kV) and very low current (a few pA) because they can keep an image resolution good enough even in these extreme conditions) and thus the original characteristics of the samples may be preserved for further testing or manipulation (no conductive coating in particular).
3. Results
In order to correlate the birefringence to the existence of porous nanogratings, we have analyzed the laser tracks cross sections using SEM images in two different writing configurations noted Xx and Xy, namely parallel and perpendicular polarization to writing direction. In addition for better investigation, we have studied two parameters dependence: the pulse energy and the overlapping rate that is defined by the ratio of the laser repetition rate to the writing speed.
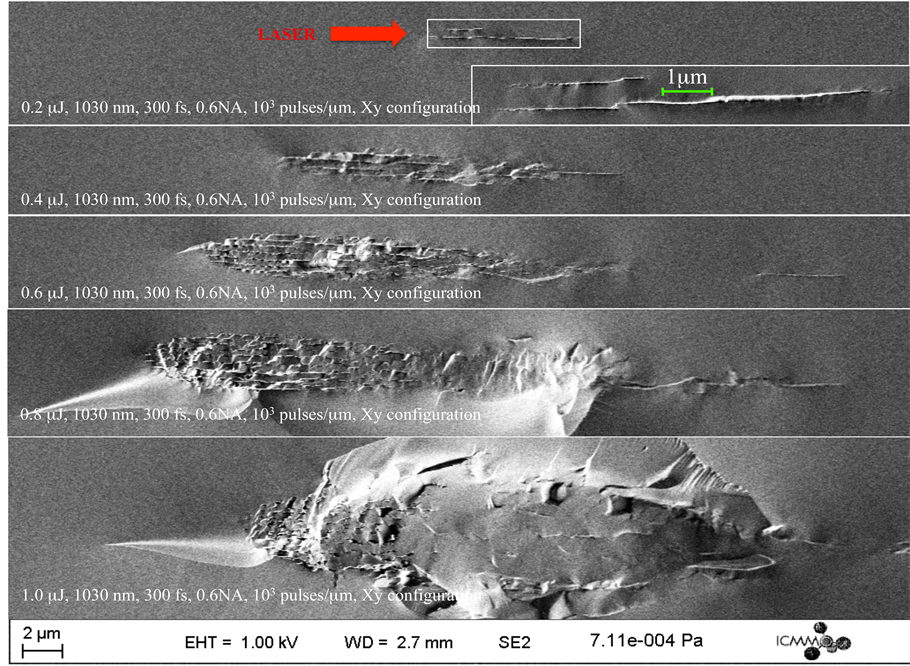
The FEG-SEM secondary electrons images shown in Figure 2 highlight the modifications morphology occur
Figure 2. FEG-SEM, secondary electrons images of laser tracks cross-section for perpendicular writing configuration. The laser parameters were: 1030 nm, 300 fs, 0.6 NA and 103 pulses/μm and Xy configuration.
ring above T2 threshold for different pulse energy. The laser polarization was perpendicular to writing direction in order to reveal the nanoplanes or so-called nanogratings in the literature. Firstly, there is a trend towards increasing widths and lengths of the modified regions as the pulse energy increases from 0.2 to 1 μJ. In particular, we can observe that the number of nanoplanes in increasing along the width of the laser tracks. At low energy, we observe only 2 nanoplanes in the laser propagation direction for the studied overlapping rate that has been fixed at 103 pulses/micron. Then, above 0.6 μJ, disruptive modulation of the nanoplanes builds up in the head of the modified regions and becomes massive as the pulse energy is increased up to 1 μJ and above.
For a deeper investigation of the nanoplane structure, we turned the laser polarization 90˚ into a parallel configuration Xx (i.e. laser polarization is parallel to the scanning direction). As shown in Figure 3, when the laser polarization is parallel to the scanning direction, one can directly image the modified region inside the nanoplanes of the head of the interaction volume. The image is not uniform in term of nanoporosity and we observed what appears to be a “white” layer arising from surface topography variations that corresponds to material between the nanolayers. In all our samples, we observed that these pores always occur along with nanoplane formation for pulse energies higher than 0.2 μJ. The observed morphology is similar to the perpendicular configuration in terms of laser track lengths and widths.
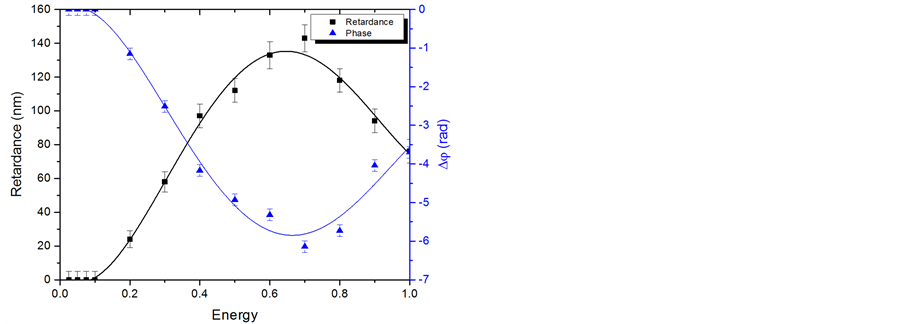
The retardance of those laser tracks was then measured by using the Sénarmont method as shown in Figure 4(a). The pulse energy used in these experiments varied from 0.025 to 1 μJ. First, measurements highlight no retardance produced below 0.2 μJ/pulse, which confirms the previous measurement in the same irradiation conditions [6] . Then, the retardance increases up to 0.7 μJ/pulse and decreases for higher pulse energies. We observe the opposite phenomena with the QPm measurements, which consist in the difference of phase in non-irradiated substrate compared to the irradiated one. The phase difference is zero below 0.2 μJ/pulse, then decreases down to
Figure 3. FEG-SEM, Secondary electrons images of laser tracks cross-section for parallel writing configuration. The laser parameters were: 1030 nm, 300 fs, 0.6 NA and 103 pulses/μm and Xx configuration.
-2p at 0.7 μJ/pulse and increases at higher pulse energy.
In order to deduce the quantitative birefringence from the retardance measurements, we need to determine the length (or the thickness) of the birefringent zone from the SEM images. The total length Lt of the laser tracks and the length Lnano of the nanostructured area (i.e. the porous nanoplane zone) are reported in Figure 4(b). The whole laser track length (including head and tail) in increasing monotonously with the pulse energy whereas the length of the nanostructured area increases up to 0.6 μJ and then decreases for higher energy. We can notice that Lnano curve exhibits the same qualitative shape as for the measured retardance shown in Figure 4(a).
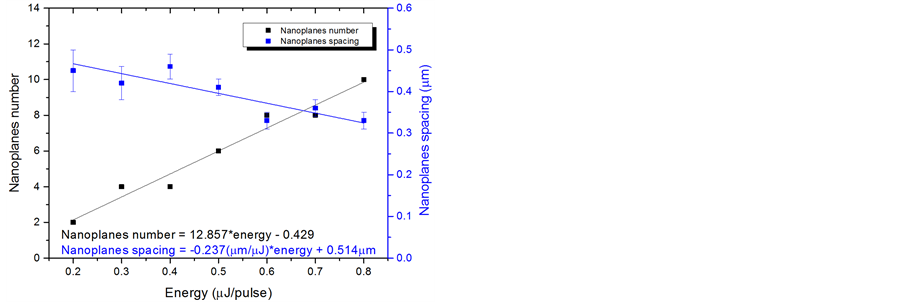
Next, in order to correlate the birefringence to the porous nanogratings characteristics, SEM images where analysed in order to deduce the nanoplanes and porosity changes according to the laser parameters. In perpendicular configuration Xy, we can see that the number of nanoplanes within the laser track width increases linearly from 0.2 μJ up to 1 μJ as reported in Figure 5(a). At the same time, measurements extracted from SEM images reveal that the average spacing between nanoplanes is decreasing from 450 nm down to 330 nm when increasing the pulse energy up to 1 μJ. This last observation is in agreement with the literature [20] . From the data gathered in parallel configuration Xx we can deduce that the average pore size increases from 16 to 50 nm to 0.4 μJ/pulse and then decrease to 35 nm at higher energy as shown in Figure 5(b). In contrast, the 2D porosity-filling factor of the nanoplans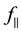 , defined by ratio between area of pores and the remaining area within a
, defined by ratio between area of pores and the remaining area within a
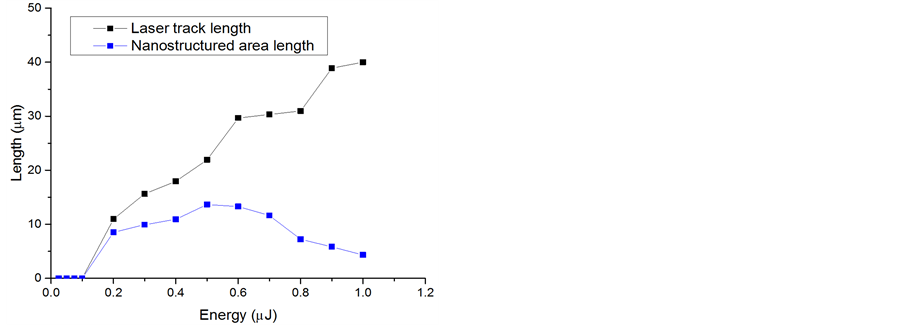
Figure 4. Detailed analyses of laser track (a) Plot of the retardance (black curve) and phase (blue curve) according to pulse energy for parallel writing configuration. (b) Plot of laser tracks length and nanostructured area length (the error bar ±1.0 μm). The laser parameters were: 1030 nm, 300 fs, 0.6 NA, 103 pulses/μm and Xx configuration.
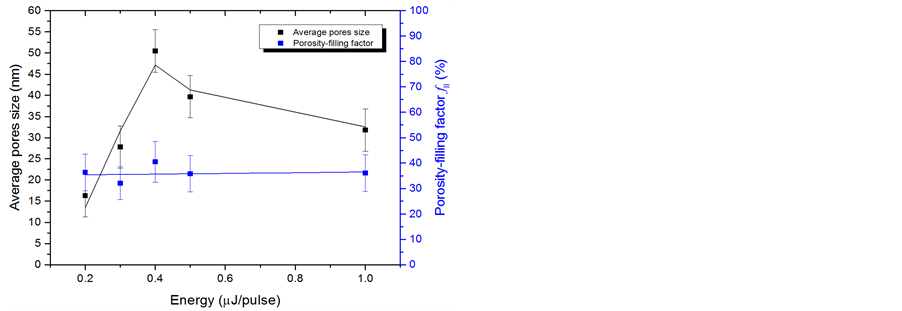
Figure 5. Structural characterization by means of SEM images: (a) Plot of the nanoplanes number and spacing according pulse energy for perpendicular writing configuration. (b) Plot of the porosity-filling factor  and average pores size according pulse energy for parallel writing configuration. The laser parameters were: 1030 nm, 300 fs, 0.6 NA, 103 pulses/μm.
and average pores size according pulse energy for parallel writing configuration. The laser parameters were: 1030 nm, 300 fs, 0.6 NA, 103 pulses/μm.
nanoplane, is independent of the laser pulse energy within the studied range. The porosity-filling factor is found to be around 36% ± 7% whatever the pulse energy may be.
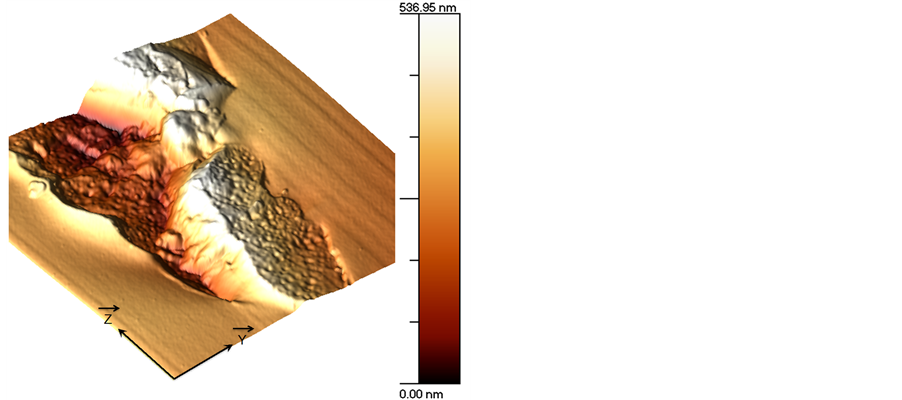
The FEG-SEM images in Figure 6 demonstrate the modification in the transformation morphology occurring for a parallel configuration Xx and for different overlapping rates (or pulse densities). The pulse energy was fixed to 0.5 μJ. For low or no overlapping rate i.e. 1 pulse/μm, only isotropic index changes are detected by optical microscopy and no specific nanostructure can be observed using SEM apart a slight contrast related to volume change. Then for overlapping rate in the range of 2 - 20 pulses/μm we detect a topographic contrast e.g. see the white area. FEG-SEM also detects some kind of bubbles that evolves into elongated ones (1 micron in length and 100 nm wide) when increasing the overlapping from 2 to 5 pulses/μm. Finally the nanoplanes are porous for overlapping rate higher than 100 pulses/micron and up to 2 × 105 pulses/μm. Notice that for low repetition rate i.e. 1 - 10 kHz, porous nanoplanes are also observed if the writing speed is small enough i.e. below 10 μm/s. Figure 7 highlights a specific laser track in SEM and its corresponding surface topography recorded in AFM as shown in Figure 7(b). The area appearing white is dense matter, although having been irradiated, whereas the parts that present “roughness” are the cleaved nanoplanes.
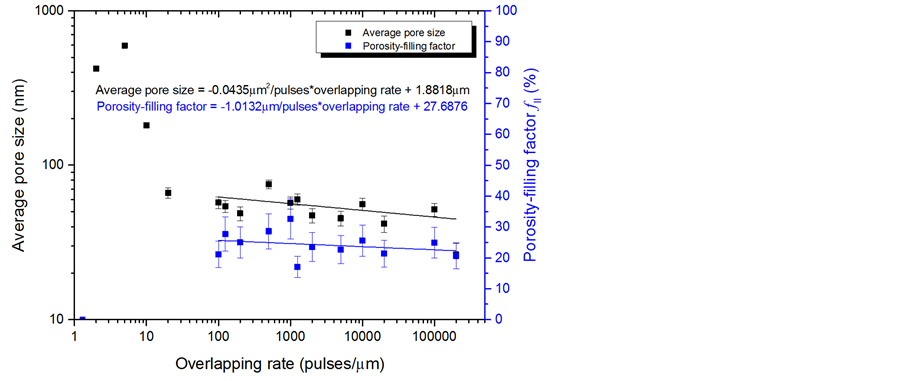
After SEM images analysis we have plotted in Figure 8 the average pore size together with the porosity-fill- ing factor 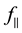 according to the overlapping rate. The average pore size is strongly decreasing from 1 - 1000 pulses/μm and it decreases from 62 nm down to 45 nm for higher overlapping rate. In contrast, the porosity- filling factor of 24% ± 5% is rather independent of overlapping rate for more than 100 pulses/μm.
according to the overlapping rate. The average pore size is strongly decreasing from 1 - 1000 pulses/μm and it decreases from 62 nm down to 45 nm for higher overlapping rate. In contrast, the porosity- filling factor of 24% ± 5% is rather independent of overlapping rate for more than 100 pulses/μm.
4. Discussion
For an irradiated area larger than the probe beam, it is well known that the strength of form birefringence de-
Figure 6. FEG-SEM, Secondary electrons images of laser tracks cross-section for parallel writing configuration, according to overlapping rate in pulses/μm. The laser parameters were: 0.5 μJ/pulse, 1030 nm, 300 fs, 0.6 NA and Xx configuration.
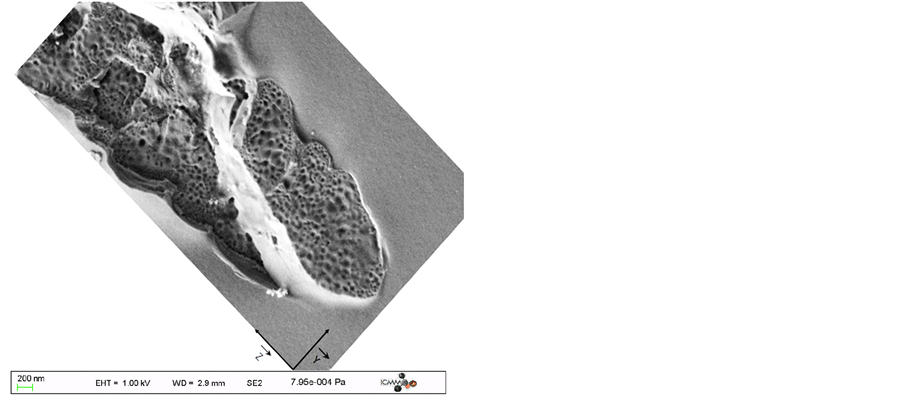
Figure 7. FEG-SEM, Secondary electrons image (a) and 3D AFM image 3.6 μm × 3.6 μm (b) of a laser track cross-section for parallel writing configuration. The laser parameters were: 0.4 μJ/pulse, 1030 nm, 300 fs, 0.6 NA, 103 pulses/μm and Xx configuration.
Figure 8. Plot of porosity-filling factor 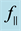
pends on the nanoplanes spacing, the nanolayers thicknesses (t1 and t2) and the refractive indices (n1 and n2) of these two nanolayers. The uniaxial birefringence Dn due to the nanogratings can be written as a refractive index difference between ordinary (n0) and extraordinary (ne) wave [21] :

where 
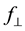
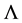
n2, t1 and t2 are defined in Figure 1 and Figure 10. This relation, valid for nanogratings, can be generalised for any anisotropic structures like series of nanoplanes, in the case where the probe beam diameter w is larger than nanoplanes area:
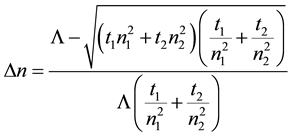
and, in the case where w is smaller than nanoplane area:
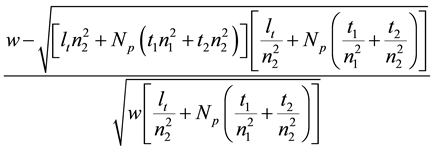
where Np is the number of period 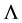
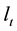
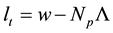
On the other hand, QPm gives a measurement that is proportional to the mean refractive index defined by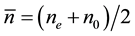

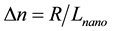
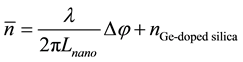
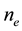
that we can solve:
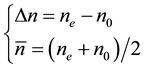
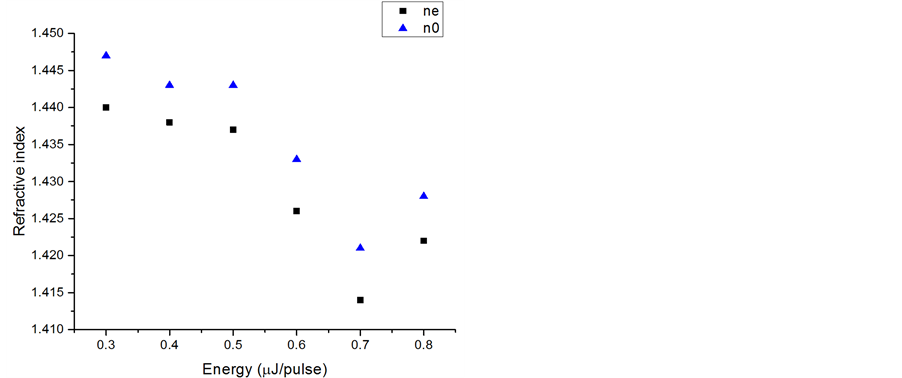
The Figure 9(a) shows the result after solving the above equations set. We observe that both ordinary and extraordinary refractive indices decrease down to 0.7 μJ/pulse and seem increase to higher energies. The maximum decrease is around −4 × 10−2 and maximum birefringence Dn is around −7 × 10−3. This order of magnitude is in agreement with previous publication from E. Bricchi et al. [21] .
From these experimental results, we can extract information about the matter within the porous nanoplanes
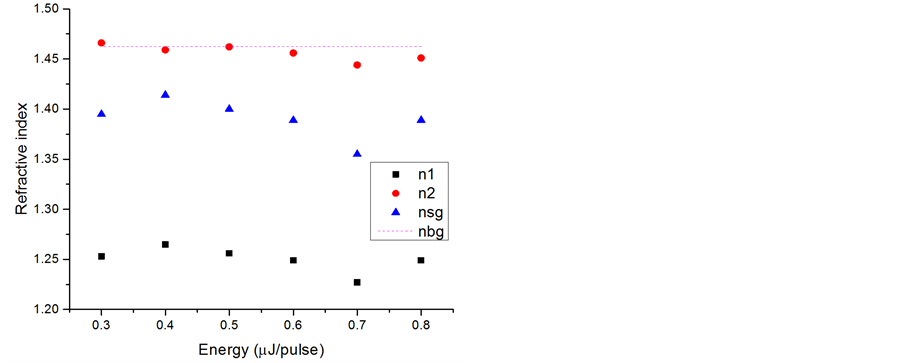
Figure 9. Refractive indices deduced from the measurements: (a) Ordinary no and extraordinary ne indices, (b) n1 and n2, local indices of the plates of thickness t1 and t2, respectively and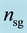

and the matter around them. As shown in Figure 10, these periodic structures are ruled in the direction perpendicular to the polarization of the writing laser and consist of thin regions of refractive index n1, characterized by a strong oxygen deficiency and oxide decomposition [6] , surrounded by larger regions of index n2. Using Equation (1) we can thus deduce 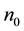
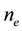

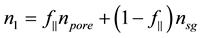
where 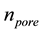
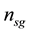
Figure 9(b) shows that the refractive index 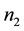
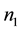
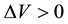
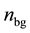
5. Conclusions
Here, we analyzed the laser tracks in the condition for obtaining porous nanogratings and related anisotropic optical properties at the nanoscopic scale. We revealed that the magnitude of the birefringence could be accurately modeled based on SEM observations with the following input parameters: number of nanoplanes, nanoplanes thickness, nanostructuration length, and the porosity-filling factor. This study reveals definitely that modification of birefringence is mainly due to the structural modification (number of nanoplanes, their thickness and length) and not related to refractive index changes after laser irradiation according to energy or overlapping rate. It is
Figure 10. Schematic of sub-wavelength periodic structure formed in cross- section of the irradiated region. n1 and n2: local refractive indices of the plates of the thickness t1 and t2, respectively, 
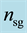
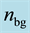
worth noticing that the matter in-between nanopores exhibits significant refractive index decrease which is likely due to fictive temperature increase and/or the presence of a significant amount of interstitial O2 in the silica surrounding nanopores.
The average pore size increases with the pulse energy and slightly decreases at high repetition rate or high overlapping rate. This should provide a way to reduce the light scattering related to the porous nanoplanes formation. From a practical perspective, such control allows the fabrication of mesoporous nanolayers that can be arranged in a nearly regular array, leading to many novel applications not only for birefringent devices (such as waveplates [22] , micro-patterned waveplates, polarization converters, 5D optical data storage) but we can also expect the catalysts, molecular sieves, encapsulants, and composites. Such mesoporous glass could also be used for filtration and separation of compounds. For example, by controlling the pore diameters and homogeneity, the mesoporous network allows permeability on a size-selective basis and can be integrated with high precision into waveguides and patterned components, a potentially more robust and efficient top-down alternative to methods based on bottom-up self-assembly.
Acknowledgements
This work has been performed in the framework of FLAG (Femtosecond Laser Application in Glasses) consortium project with the support of several organisations: the Agence Nationale pour la Recherche (ANR-09- BLAN-0172-01), the RTRA Triangle de la Physique (Réseau Thématique de Recherche Avancée, 2008-056T) and FP7-PEOPLE-IRSES (e-FLAG 247635).
Cite this paper
R.Desmarchelier,B.Poumellec,F.Brisset,S.Mazerat,M.Lancry, (2015) In the Heart of Femtosecond Laser Induced Nanogratings: From Porous Nanoplanes to Form Birefringence. World Journal of Nano Science and Engineering,05,115-125. doi: 10.4236/wjnse.2015.54014
References
- 1. Ams, M., Marshall, G., Dekker, P., Dubov, M., Mezentsev, V., Bennion, I. and Withford, M. (2008) Investigation of Ultrafast Laser-Photonic Material Interactions: Challenges for Directly Written Glass Photonics. IEEE Journal of Selected Topics in Quantum Electronics, 14, 1370-1381.
http://dx.doi.org/10.1109/JSTQE.2008.925809 - 2. Gattass, R.R. and Mazur, E. (2008) Femtosecond Laser Micromachining in Transparent Materials. Nature Photonics, 2, 219-225.
http://dx.doi.org/10.1038/nphoton.2008.47 - 3. Itoh, K., Watanabe, W., Nolte, S. and Schaffer, C. (2006) Ultrafast Processes for Bulk Modification of Transparent Materials. MRS BULLETIN, 31, 620-625.
http://dx.doi.org/10.1557/mrs2006.159 - 4. Qiu, J., Miura, K. and Hirao, K. (2008) Femtosecond laser-Induced Microfeatures in Glasses and Their Applications. Journal of Non-Crystalline Solids, 354, 1100-1111.
http://dx.doi.org/10.1016/j.jnoncrysol.2007.02.092 - 5. Lancry, M., Poumellec, B., Chahid-Erraji, A., Beresna, M. and Kazansky, P. (2011) Dependence of the Femtosecond Laser Refractive Index Change Thresholds on the Chemical Composition of Doped-Silica Glasses. Optical Materials Express, 1, 711-723.
http://dx.doi.org/10.1364/OME.1.000711 - 6. Poumellec, B., Lancry, M., Chahid-Erraji, A. and Kazansky, P. (2011) Modification Thresholds in Femtosecond Laser Processing of Pure Silica: Review of Dependencies on Laser Parameters. Optical Materials Express, 1, 766-782.
http://dx.doi.org/10.1364/OME.1.000766 - 7. Eaton, S., Zhang, H., Herman, P., Yoshino, F., Shah, L., Bovatsek, J. and Arai, A. (2005) Heat Accumulation Effects in Femtosecond Laser-Written Waveguides with Variable Repetition Rate. Optics Express, 13, 4708-4716.
http://dx.doi.org/10.1364/OPEX.13.004708 - 8. Schaffer, C., Brodeur, A., Garcia, J. and Mazur, E. (2001) Micromachining Bulk Glass by Use of Femtosecond Laser Pulses with Nanojoule Energy. Optics Letters, 26, 93-95.
http://dx.doi.org/10.1364/OL.26.000093 - 9. Bricchi, E., Klappauf, B. and Kazansky, P. (2004) Form Birefringence and Negative Index Change Created by Femtosecond Direct Writing in Transparent Materials. Optics Letters, 29, 119-121.
http://dx.doi.org/10.1364/OL.29.000119 - 10. Poumellec, B., Lancry, M., Poulin, J. and Ani-Joseph, S. (2008) Non Reciprocal Writing and Chirality in Femtosecond Laser Irradiated Silica. Optics Express, 16, 18354-18361.
http://dx.doi.org/10.1364/OE.16.018354 - 11. Sudrie, L., Franco, M., Prade, B. and Mysyrowicz, A. (1999) Writing of Permanent Birefringent Microlayers in Bulk Fused Silica with Femtosecond Laser Pulses. Optics Communications, 171, 279-284.
http://dx.doi.org/10.1016/S0030-4018(99)00562-3 - 12. Lancry, M., Niay, P. and Douay, M. (2005) Comparing the Properties of Various Sensitization Methods in H2-Loaded, UV Hypersensitized or OH-Flooded Standard Germanosilicate Fibers. Optics Express, 13, 4037-4043.
http://dx.doi.org/10.1364/OPEX.13.004037 - 13. Lancry, M. and Poumellec, B. (2013) UV Laser Processing and Multiphoton Absorption Processes in optical Telecommunication Fibers Materials. Physics Reports, 523, 207-229.
http://dx.doi.org/10.1016/j.physrep.2012.09.008 - 14. Eaton, S.M., Ng, M.L., Osellame, R. and Herman, P.R. (2010) High Refractive Index Contrast in Fused Silica Waveguides by Tightly Focused, High-Repetition Rate Femtosecond Laser. Journal of Non-Crystalline Solids.
- 15. Bricchi, E. and Kazansky, P. (2006) Extraordinary Stability of Anisotropic Femtosecond Direct-Written Structures Embedded in Silica Glass. Applied Physics Letters, 88, 111119-111119.
http://dx.doi.org/10.1063/1.2185587 - 16. Shimotsuma, Y., Kazansky, P., Qiu, J. and Hirao, K. (2003) Self-Organized Nanogratings in Glass Irradiated by Ultrashort Light Pulses. Physical Review Letters, 91, Article ID: 247405.
http://dx.doi.org/10.1103/PhysRevLett.91.247405 - 17. Bhardwaj, V., Simova, E., Rajeev, P., Hnatovsky, C., Taylor, R., Rayner, D. and Corkum, P. (2006) Optically Produced Arrays of Planar Nanostructures Inside Fused Silica. Physical Review Letters, 96, Article ID: 057404.
http://dx.doi.org/10.1103/PhysRevLett.96.057404 - 18. Canning, J., Lancry, M., Cook, K., Weickman, A., Brisset, F. and Poumellec, B. (2011) Anatomy of Femtosecond Laser processed Silica Waveguide. Optical Materials Express, 1, 998-1008.
http://dx.doi.org/10.1364/OME.1.000998 - 19. Lancry, M., Poumellec, B., Canning, J., Cook, K., Poulin, J.C. and Brisset, F. (2013) Ultrafast Nanoporous Silica Formation Driven by Femtosecond Laser Irradiation. Laser & Photonics Reviews, 7, 953-962.
http://dx.doi.org/10.1002/lpor.201300043 - 20. Yang, W.J., Bricchi, E., Kazansky, P.G., Bovatsek, J. and Arai, A.Y. (2006) Self-Assembled Periodic Sub-Wavelength Structures by Femtosecond Laser Direct Writing. Optics Express, 14, 10117-10124.
http://dx.doi.org/10.1364/OE.14.010117 - 21. Bricchi, E., Klappauf, B.G. and Kazansky, P.G. (2004) Form Birefringence and Negative Index Change Created by Femtosecond Direct Writing in Transparent Materials. Optics letters, 29, 119-121.
http://dx.doi.org/10.1364/OL.29.000119 - 22. Lancry, M., Desmarchelier, R., Cook, K., Canning, J. and Poumellec, B. (2014) Compact Birefringent Waveplates Photo-Induced in Silica by Femtosecond Laser. Micromachines, 5, 825-838.
http://dx.doi.org/10.3390/mi5040825