World Journal of Nano Science and Engineering
 Vol.3 No.3(2013), Article ID:36672,5 pages DOI:10.4236/wjnse.2013.33007

Density Functional Study of the Cluster Model of SnO2(110) Surface Modified by Benzoic Acids

Tegshjargal Khishigjargal1, Namsrai Javkhlantugs1,2, Chimed Ganzorig2, Youji Kurihara1, Masaru Sakomura1, Kazuyoshi Ueda1*

1Department of Advanced Materials Chemistry, Graduate School of Engineering, Yokohama National University, Yokohama, Japan

2Center for Nanoscience and Nanotechnology & Department of Chemical Technology, School of Chemistry and Chemical Engineering, National University of Mongolia, Ulaanbaatar, Mongolia

Email: k-ueda@ynu.ac.jp

Copyright © 2013 Tegshjargal Khishigjargal et al. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.

Received June 26, 2013; revised July 26, 2013; accepted August 2, 2013

Keywords: Benzoic Acid Derivatives; Dipole Moment; Work Function Change; Cluster Model; Modification of Surface

ABSTRACT

The properties of the modified surface of SnO2(110) with benzoic acid (Y-C6H4-COOH: Y is para position relative to -COOH group) derivatives were investigated using density functional theory. Zehner et al. mentioned that the modification of surface dipole moment made it possible to tune the work function of the system. The experiment of Ganzorig et al. showed that there was a linear relationship between the dipole moment of the binding molecule and the work function change of the system using the modified surface of indium-tin oxide (ITO) with some benzoic acid derivatives. To elucidate the relation between the dipole moment of the molecule and the work function change, we investigated the modified surface of SnO2(110) using Sn7O14 cluster model which was embedded in the fixed point charges. On the modification of the surface, benzoic acid derivatives were bound to SnO2 surface. By changing the terminal group of benzoic acid with H, Cl, F, CF3 and CCl3, the work function changed and the dipole moment of the binding molecules of the modified SnO2(110) were evaluated. The results showed that there was a linear relationship between the dipole moment of the binding molecules and the work function changed. From this relation, the average value of the dipole moments of Sn-OOC linkage at the surface was also evaluated.

1. Introduction

The tuning of the work function of metal oxide is important in the research on the application field of the electronic devices [1]. The modification of the surface with self assembled monolayer (SAM) has been known as a method to change the work function of the metal oxide substrates [2,3]. One of such metal oxide substrates is tin oxide (SnO2), which has been used for gas sensors, transparent conductors, and catalysts [4]. The (110) surface of SnO2 is the thermodynamically most stable face compared to other low index faces of tin dioxide and has been investigated not only experimentally [5-8] but also theoretically the properties of its surface [9-15]. Many researchers studied molecular adsorption and oxygen vacancies of tin dioxide surface theoretically [16,17] to interpret how tin dioxide surfaces sense gases [18] and conduct electric current [19]. In this work, we studied the work function change of the SnO2(110) surface using the density functional theory (DFT) with the cluster model of SnO2(110) where surface was modified by various benzoic acid derivatives.

If SAM is conceptualized as parallel charged sheets, the work function change (ΔΦ) can be expressed by the following equation [20]

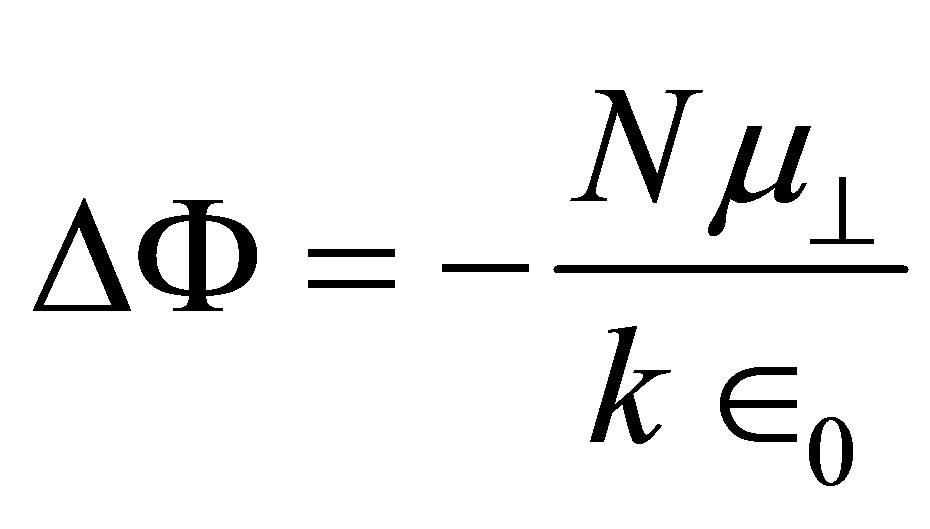(1)

where N is the density of the molecules on the surface; 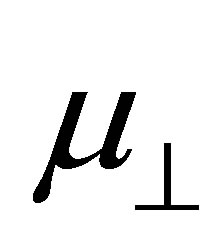is the component of the dipole moment of SAM normal to the surface; k is the dielectric constant of the dipole layer; and 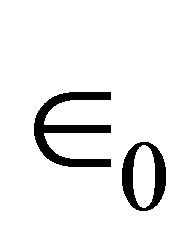is the permittivity of vacuum. By assuming the chemisorbed SAMs are modeled as two dipole sheets with different dielectric constants, Zehner et al. derived the Equation (2) for work function change (ΔΦ) of the chemisorptions of SAM from a series of arenethiol adsorbates on the gold [20].

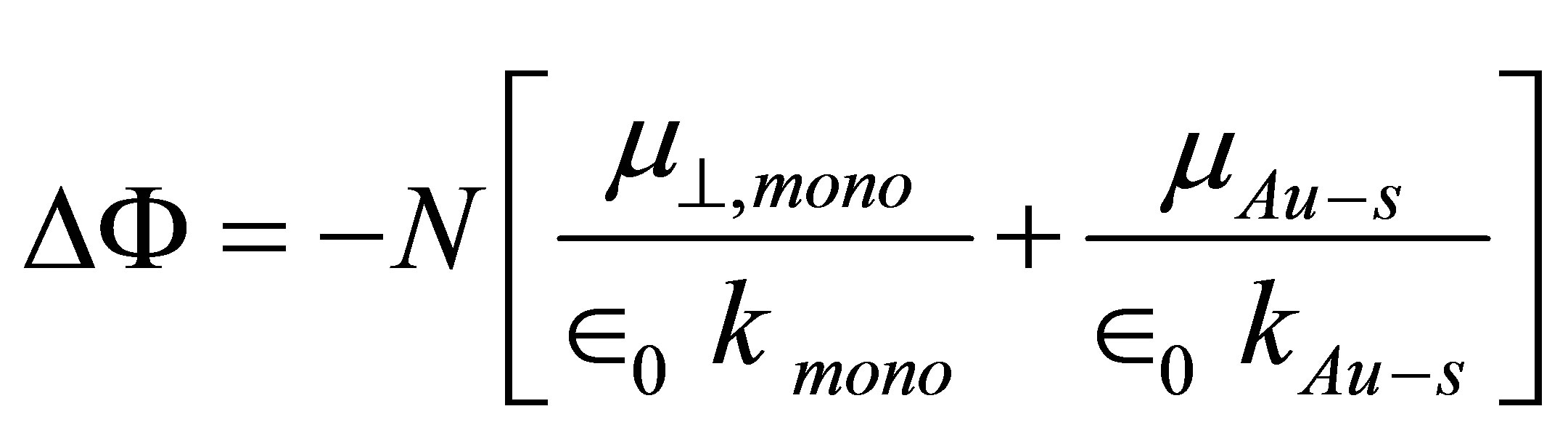(2)

where 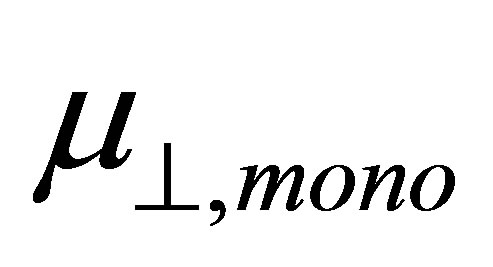is the dipole moment of the chemisorbed molecule normal to the surface plane, and, kAu−S, and kmono are the dipole moment of Au-S bond, dielectric constant of Au-S bond, and dielectric constant of monolayer, respectively. They were determined independently according to Zehner et al. [20]. If we apply this equation to the system of SnO2 surface modified by benzoic acid molecules, the following equation can be formed

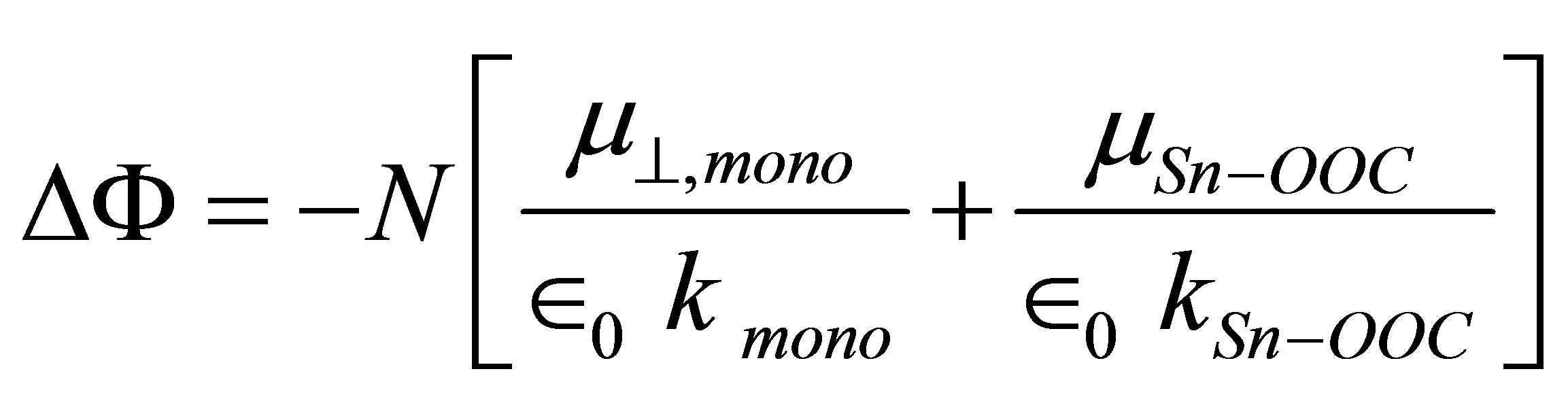(3)

where is the dipole moment of the modified monolayer component normal to SnO2(110) surface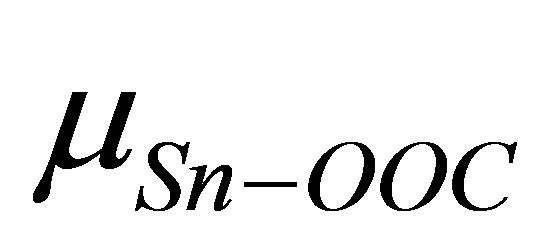, and and 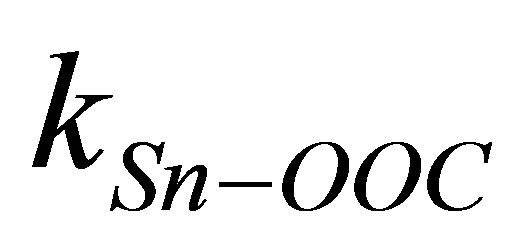are the dipole moment and the dielectric constant of Sn-OOC bonds, respectively. As there are no existing experimental values of surface density (N) and the work function change (ΔΦ) of the modified SnO2(110) surface with benzoic acid derivatives, it is difficult to evaluate the work function change by these dipole moments from Equation (3) directly. Therefore, we substituted left side of Equation (3) to the right side of Equation (1), then, we derived the following equation

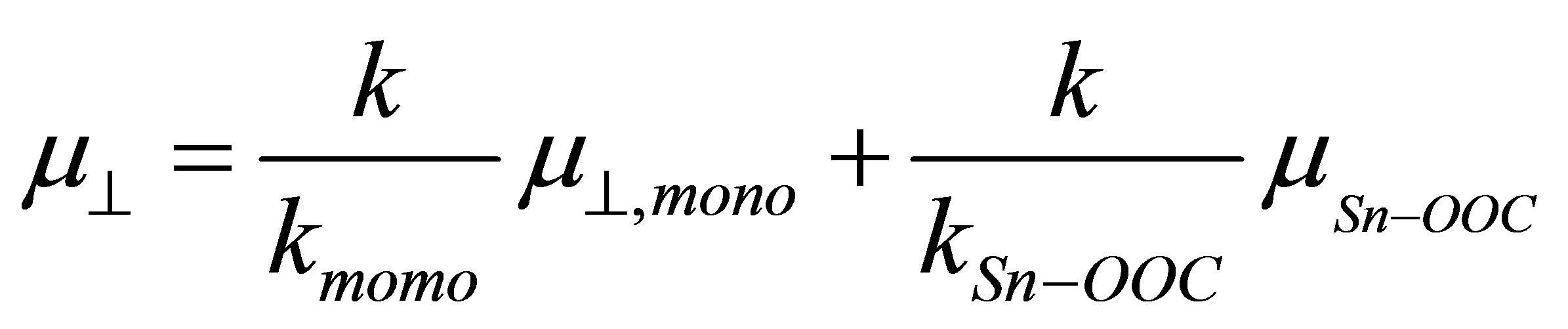(4)

If we assume the coefficient (k/kmono) of the first term and the whole second term of the right side of Equation (4) are constants, we can expect the linear relationship between 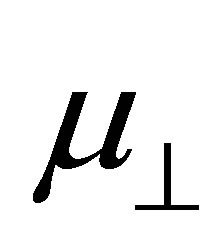and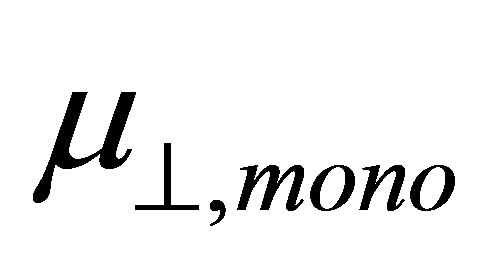. The main aim of this work is to check the relationship between them by using the first principle method. The results showed that the relation between dipole moment of 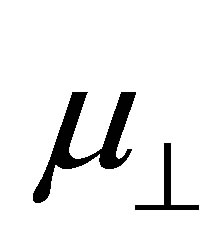and was linear.

2. Calculation Method

2.1. Calculation Procedure

DFT calculation was performed with Becke’s hybrid three parameters approach [21,22] and Lee-Yang-Parr exchange-correlation functional (B3LYP), [23] which is implemented in Gaussian03 package program, [24] was used. Basis set for Sn atom was chosen by a relativistic effective core potential (ECP) [25] with double zetta function (LanL2DZ) which treats 1s2 to 4p6 electrons are frozen and 5s25p2 electrons are explicitly included in the valence. For H, C, O, F and Cl atoms, basis set of 6-31G were used [26]. During the optimization, the atoms of the cluster of Sn7O14 were frozen and their geometric positions were the same as crystal geometry [27].

2.2. Calculation Model

The surface of SnO2(110) was modeled as a cluster of Sn7O14 embedded in point charges (PCs) according to the model of Melle-Franco and Pacchioni (Figure 1) [28]. In this figure, PCs are illustrated by wire model with +2 and −1 electrons substituted in positions of Sn and O atoms in the bulk geometry of SnO2, respectively [27]. This cluster model corresponds to the stoichiometric surface structure of SnO2(110).

The binding structure of the benzoic derivative YC6H4-COOH (Y: H, F, Cl, CCl3, CF3) on the SnO2 surface was modeled and shown in Figure 2.

Calatayud et al. [29] calculated the methanol adsorption on SnO2(110) surface. They modeled the cleavage of the methanol O-H bond and the resulting fragments of H and CH3O were bounded to the bridging oxygen (Ob) and 5-fold tin (Sn5) atoms, respectively. According to their model, we modeled the cleavage of benzoic acid COO-H bond and the resulting fragments of H and COO were bound to the same bridging oxygen (Ob) as Calatayud et al. model [29] and 5-fold tin (Sn5) atoms to make the system with singlet multiplicity as were shown in Figure 2, respectively.

3. Results and Discussion

Modified surface structures, where the benzoic acid derivatives of Y-C6H4-COOH (Y: H, F, Cl, CCl3 and CF3)

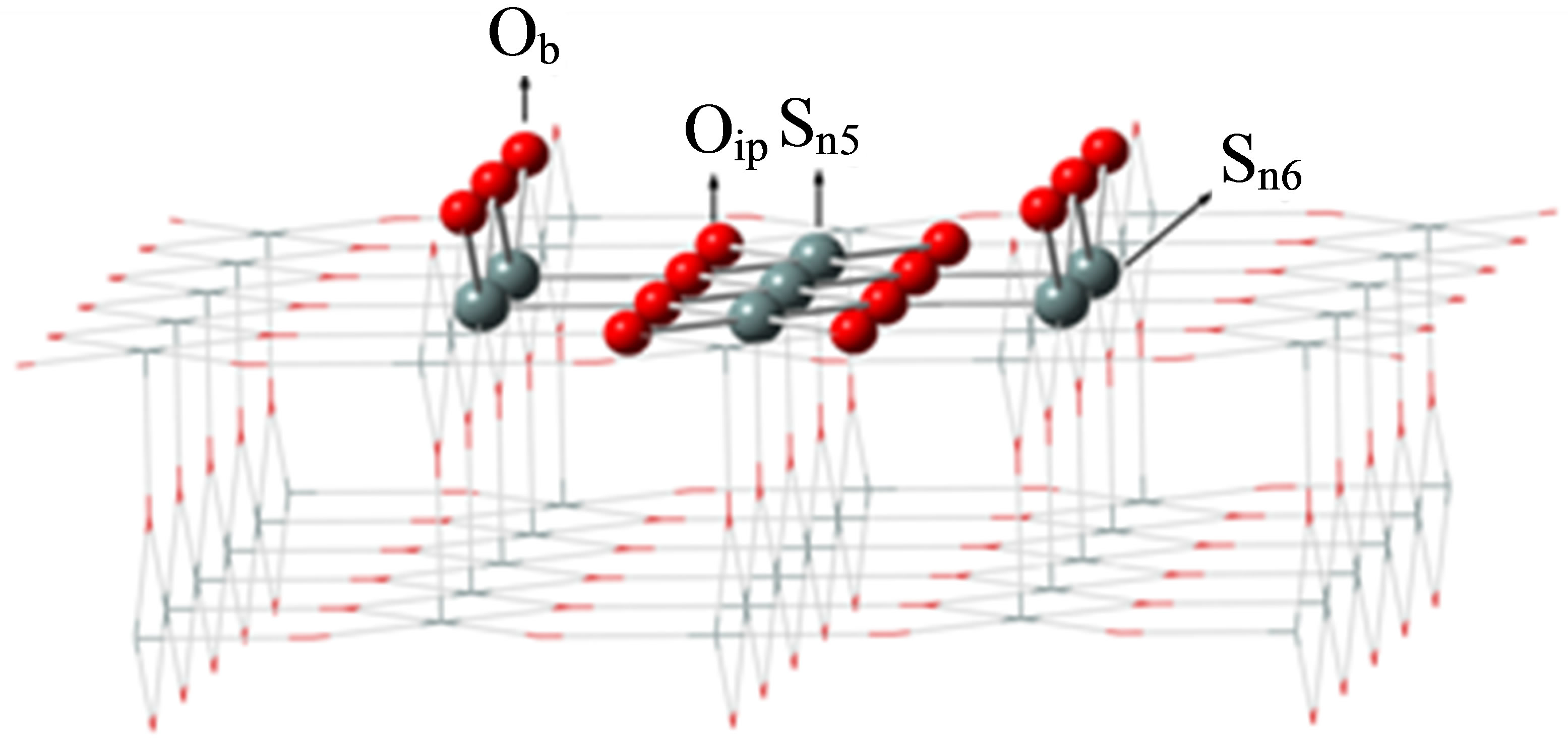
Figure 1. Structure of the Sn7O14 cluster model embedded in a point charge potential. Sn5; 5-fold tin, Sn6; 6-fold tin, Ob; bridging oxygen, Oip; in-plane oxygen atoms.

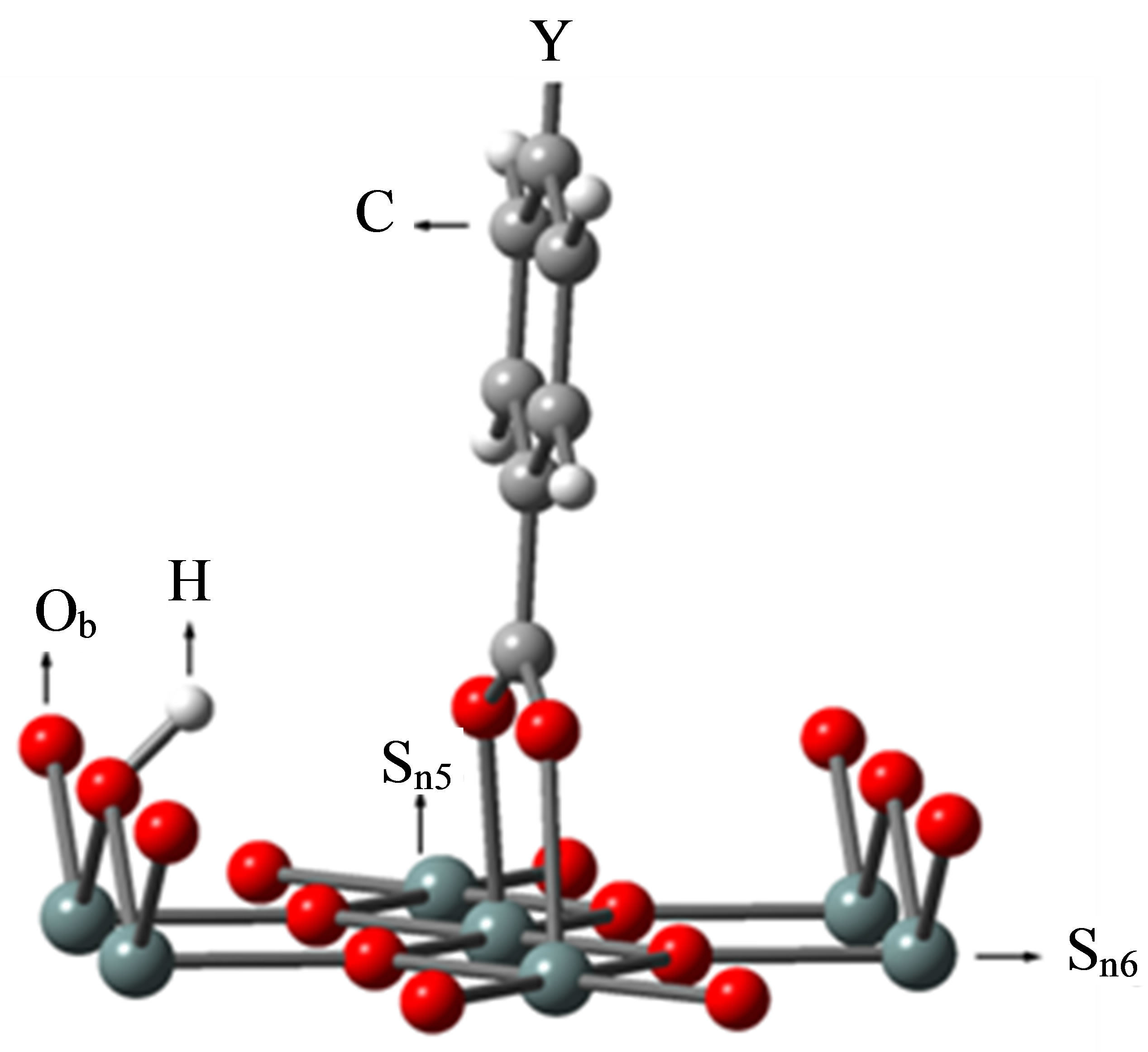
Figure 2. The binding structure of Y-C6H4-COOH after optimization. PCs are not shown for simplicity.

bind to the SnO2 surface, were investigated using DFT calculation. As the fragments of the cleavage of benzoic acid derivatives of H and Y-C6H4-COO were modeled to bind to the bridging oxygen (Ob) and the 5-fold tin (Sn5) atoms, the bound structures were first optimized to check the adequacy of its binding structure. In the optimization, surface atoms of the Sn7O14 cluster were fixed in the calculation. After the successful optimization of the binding structures of Y-C6H4-COO on Sn7O14-H cluster, it was found that the plane of benzene ring was oriented close to normal to the SnO2(110) surface. By using the optimized bound structure, dipole moments perpendicular to the surface of SnO2(110), 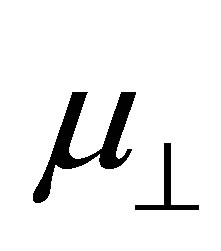, were evaluated. The obtained values were shown in Table 1. To investigate the relationship between 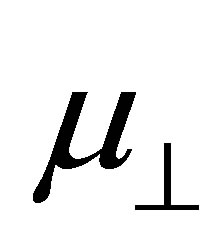and 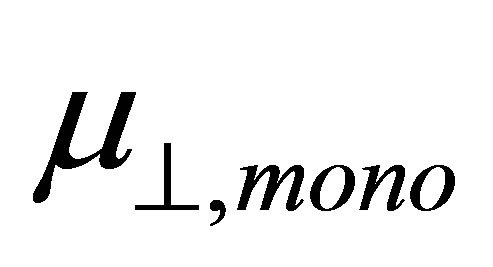shown in Equation (4), we calculated the values of the dipole moment of the modified monolayer component normal to SnO2(110) surface,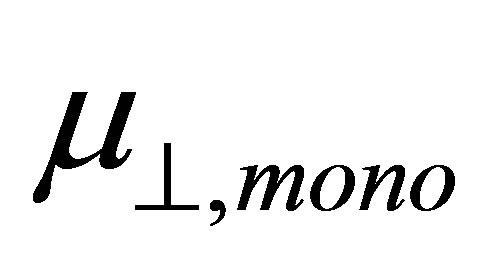. According to the model of Zehner et al. [20], 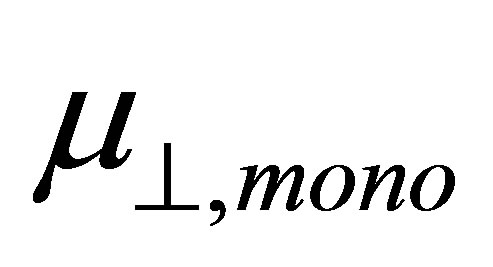corresponds to the dipole moment of Y-C6H4-COO radicals. This component of the dipole moment of Y-C6H4-COO radicals (Y: H, F, Cl, CF3, CCl3) was calculated and the dipole moments along to the normal to the surface were shown in Table 1 as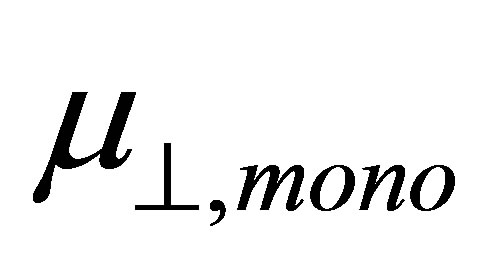. The relation between the dipole moment of 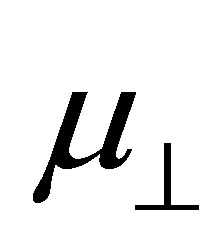and 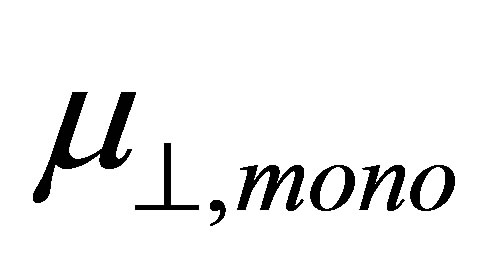is shown in Figure 3. It shows that there is a good linear relationship between these two dipole moments. The square of the correlation coefficient is 0.998. The value of the slope is 1.102 and the intercept is −22.1 D. As the slope value is close to 1, we can estimate from Equation (4) that the value of k is almost similar to kmono. On the other hand, the intercept value of −22.1 D corresponds to (k/kSn-OOC) term in equation 4. If we assume the values of k and kSn-OOC are also equal, the dipole moment for the Sn-OOC bonds, µSn-OOC, can be estimated. The evaluated value of µSn-OOC is −22.1 D.

It shows that the contribution of the binding group -COO to the surface dipole moment is constant in the series of Y-C6H4-COO molecules, even though the terminal groups of Y in the Y-C6H4-COO molecules are different. Carrara et al. [30] investigated the surface adsorption of carboxylic acid derivatives on both aluminium and indium-tin oxide surfaces and reported that the contribution of the binding group of -COO to the surface permanent dipole is relevant and +0.7 D and −2.2 D respectively in each series. Zehner et al. obtained the value of 2.3 - 3.8 D for some series of thiols on Au surface [20]. Compared to their values, the evaluated value of −22.1 D seems a little large. However, two Sn-OOC bonds are involved in the linkage in this model. By using the partial charges of Sn and oxygen of the carboxyl group, which were evaluated in this model, Sn-O average dipole moment was roughly estimated 12.11 D by using two Sn-O bonds for all five terminal groups (Y: H, F, Cl, CF3, CCl3). As two Sn-OOC bonds are involved in the linkage at the surface, the estimation of the dipole moment for the Sn-OOC bonds, µSn-OOC, value seems to be reasonable.

By using Equation (3), work function change can be estimated. As the value of the surface molecular density N can not be found in the literature, the value of 1.3 × 1014 cm−2, which was measured for nitrobenzoic acid by Langmuir isotherms, [31] was used as a rough estimation value for our cluster Sn7O14 model. kmono and kSn-OOC were chosen as benzoic acid dielectric constant equals to 2.5 [31]. The obtained work function changes are shown

Figure 3. Relationship between the calculated dipole moments of µ┴ and µ┴,mono.

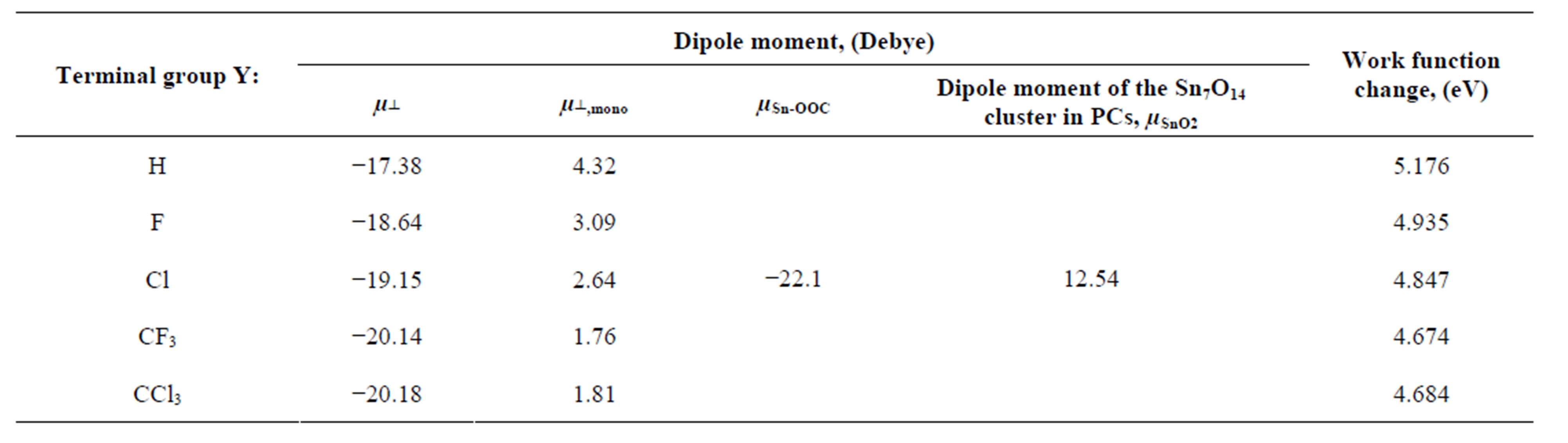
Table 1. Calculated dipole moments normal to the SnO2(110) surface.

in Table 1. Calculated values of work function change are large compared to the experimentally observed work function changes obtained by Nüesch et al. [30,31] and Appleyard et al. [32] on ITO and Aluminium surfaces graftification. Further calculation works on different series of metal oxide surfaces and the experimental work on the work function change and the molecular density of chemisorbed SAM should be desired.

4. Conclusion

Density functional calculation on the modified surface of SnO2(110) with benzoic acid derivatives was performed to obtain the information of the surface dipole moment and the work function changed using the cluster model. The result shows the linear relationship between the surface dipole moment 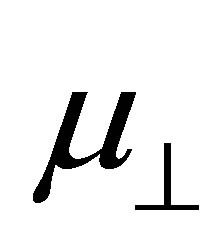and the dipole moment of binding molecule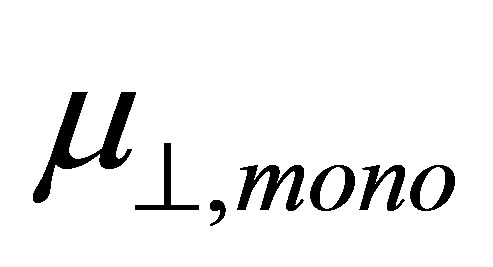. From this relation, dipole moment of the linkage of the Sn and OOC bonds at the surface was evaluated and the average value of −22.1 D was obtained.

5. Acknowledgements

The authors thank the Research Center for Computational Science, Okazaki, Japan for the use of a computer to perform part of the calculation.

REFERENCES

  1. M. Batzill, K. Katsiev and U. Diebold, “Tuning the Oxide/Organic Interface: Benzene on SnO2(101),” Applied Physics Letters, Vol. 85, No. 23, 2004, pp. 5766-5768. doi:10.1063/1.1831565
  2. C. Ganzorig and M. Fujihara, “Chemically Modified Oxide Electrodes. Encyclopedia of Electrochemistry,” WileyVCH Verlag GmbH & Co. KGaA, city, 2007. doi:10.1002/9783527610426.bard100107
  3. Ch. Ganzorig, K.-J. Kwak, K. Yagi and M. Fujihira, “Fine Tuning Work Function of Indium Tin Oxide by Surface Molecular Design: Enhanced Hole Injection in Organic Electroluminescent Devices,” Applied Physics Letters, Vol. 79, No. 2, 2001, pp. 272-274. doi:10.1063/1.1384896
  4. M. Batzil and U. Diebold, “The Surface and Materials Science of Tin Oxide,” Progress in Surface Science, Vol. 79, No. 2-4, 2005, pp. 47-154. doi:10.1016/j.progsurf.2005.09.002
  5. E. De Frésart, J. Darville and J. M. Gilles, “Influence of the Surface Reconstruction on the Work Function and Surface Conductance of (110)SnO2,” Application of Surface Science, Vol. 11-12, 1982, pp. 637-651. doi:10.1016/0378-5963(82)90109-X
  6. J. M. Themlin, R. Sporken, J. Darville, R. Caudano, J. M. Gilles and R. L. Johnson, “Resonant-Photoemission Study of SnO2: Cationic Origin of the Defect Band-Gap States,” Physical Review B, Vol. 42, No 18, 1990, pp. 11914-11925. doi:10.1103/PhysRevB.42.11914
  7. B. M. S. Giambastiani, “Evoluzione Idrologica ed Idrogeologica Della Pineta di San Vitale (Ravenna),” Ph.D. Thesis, Bologna University, Bologna, 2007.
  8. D. F. Cox, T. B. Fryberger and S. Semancik, “Oxygen Vacancies and Defect Electronic States on the SnO2(110)- 1 × 1 Surface,” Physical Review B, Vol. 38, No 3, 1988, pp. 2072-2083. doi:10.1103/PhysRevB.38.2072
  9. M. Batzill, K. Katsiev, J. M. Burst and U. Diebold, “GasPhase-Dependent Properties of SnO2 (110), (100), and (101) Single-Crystal Surfaces: Structure, Composition, and Electrocnic Properties,” Physical Review B, Vol. 72, No. 16, 2005, pp. 165414-165434. doi:10.1103/PhysRevB.72.165414
  10. J. Oviedo and M. J. Gillan, “Energetics and Structure of Stoichiometric SnO2 Surfaces Studied by First-Principles Calculations,” Surface Science, Vol. 463, No. 2, 2000, pp. 93-101. doi:10.1016/S0039-6028(00)00612-9
  11. O. Wright and W. Wright, “Flying-Machine,” US Patent No. 821393, 1906.
  12. J. Oviedo and M. J. Gillan, “The Energetic and Structure of Oxygen Vacancies on the SnO2 (110) Surface,” Surface Science, Vol. 467, No. 1-3, 2000, pp. 35-48. doi:10.1016/S0039-6028(00)00776-7
  13. I. Manassids, J. Goniakowski, L. N. Kantorovich and M. J. Gillan, “The Structure of the Stoichiometric and Reduced SnO2(110),” Surface Science, Vol. 339, No. 3, 1995, pp. 258-271. doi:10.1016/0039-6028(95)00677-X
  14. A. Bouzoubaa, A. Markovits, M. O. Calatayud and C. Minot, “Comparison of the Reduction of Metal Oxide Surfaces: TiO2-Anatase, TiO2-Rutile and SnO2-Rutile,” Surface Science, Vol. 583, No 1, 2005, pp. 107-117. doi:10.1016/j.susc.2005.03.029
  15. M. A. Mäki-Jaskari and T. T. Rantala, “Theoretical Study of Oxygen-Deficient SnO2(110) Surfaces,” Physical Review B, Vol. 65, No. 24, 2002, pp. 245428-245435. doi:10.1103/PhysRevB.65.245428
  16. M. Viitala, O. Cramariuc, T. T. Rantala and V. Golovanov, “Small Hydrocarbon Adsorbates on SnO2(110) Surfaces: Density Functional Theory Study,” Surface Science, Vol. 602, No. 18, 2008, pp. 3038-3042. doi:10.1016/j.susc.2008.08.001
  17. F. Trani, M. Causà, D. Ninno, G. Cantele and V. Barone, “Density Functional Study of Oxygen Vacancies at the SnO2 Surface and Subsurface Sites,” Physical Review B, Vol. 77, No. 24, 2008, pp. 245410-245417. doi:10.1103/PhysRevB.77.245410
  18. W. Zeng, T.-M. Liu and X. F. Lei, “Hydrogen Sensing Properties of Low-Index Surfaces of SnO2 from FirstPrinciples,” Physica B, Vol. 405, No. 16, 2010, pp. 3458- 3462. doi:10.1016/j.physb.2010.05.023
  19. D. F. Cox, T. B. Fryberger and S. Semancik, “Surface Reconstructions of Oxygen Deficient SnO2(110),” Surface Science, Vol. 224, No. 1-3, 1989, pp. 121-142. doi:10.1016/0039-6028(89)90905-9
  20. R. W. Zehner, B. F. Parsons, R. P. Hsung and L. R. Sita, “Tunning the Work Function of Gold with SelfAssembled Monolayers Derived from X-[C6H4-C≡C-]nC6H4-SH (n=0, 1, 2; X= H, F, CH3, CF3, and OCH3),” Langmuir, Vol. 15, No. 4, 1999, pp. 1121-1127.
  21. A. D. Becke, “Density-Functional Thermochemistry. III. The Role of Exact Exchange,” Journal of Chemical Physics, Vol. 98, No. 7, 1993, pp. 5648-5652. doi:10.1063/1.464913
  22. A. D Becke, “Density-Functional Exchange-Energy Approximation with Correct Asymptotic Behavior,” Physical Review A, Vol. 38, No. 6, 1988, pp. 3098-3100. doi:10.1103/PhysRevA.38.3098
  23. C. Lee, W. Yang and R.G. Parr, “Development of the Colle-Salvetti Correlation-Energy Formula into a Functional of the Electron Density,” Physical Review B, Vol. 37, No. 2, 1988, pp. 785-789. doi:10.1103/PhysRevB.37.785
  24. M. J. Frisch, et al., “Gaussian 03, Revision D.02,” Gaussian, Inc., Wallingford, 2004.
  25. W. R. Wadt and P. J. Hay, “Ab Initio Effective Core Potentials for Molecular Calculations. Potentials for Main Group Elements Na to Bi,” Journal of Chemical Physics, Vol. 82, No. 1, 1985, pp. 284-298. doi:10.1063/1.448800
  26. R. Dichfield, W. J. Hehre and J. A. Pople, “Self-Consistent Molecular-Orbital Methods. IX. An Extended Gaussian-Type Basis for Molecular-Orbital Studies of Organic Molecules,” Journal of Chemical Physics, Vol. 54, No. 2, 1971, pp. 724-728. doi:10.1063/1.1674902
  27. R. W. G. Wyckoff, “Crystal Structures,” 2nd Edition, Wiley Interscience, New York, 1964.
  28. M. Melle-Franco and G. Pacchioni, “CO Adsorption on SnO2(110): Cluster and Periodic Ab Initio Calculations,” Surface Science, Vol. 461, No. 1-3, 2000, pp. 54-66. doi:10.1016/S0039-6028(00)00528-8
  29. M. Calatayud, J. Andrés and A. Beltrán, “A Theoretical Analysis of Adsorption and Dissociation of CH3OH on the Stoichiometric SnO2(110) Surface,” Surface Science, Vol. 430, No. 1-3, 1999, pp. 213-222. doi:10.1016/S0039-6028(99)00507-5
  30. M. Carrara, F. Nüesch and L. Zuppiroli, “Carboxylic Acid Anchoring Groups for the Construction of Self-Assembled Monolayers on Organic Device Electrodes,” Synthetic Metal, Vol. 121, No. 1-3, 2001, pp. 1633-1634. doi:10.1016/S0379-6779(00)00728-1
  31. F. Nüesch, F. Rotzinger, L. Si-Ahmed and L. Zuppiroli, “Chemical Potential Shifts at Organic Device Electrodes Induced by Grafted Monolayers,” Chemical Physics Letters, Vol. 288, No. 5-6, 1998, pp. 861-867. doi:10.1016/S0009-2614(98)00350-9
  32. S. F. J. Appleyard, S. R. Day, R. D. Pickford and M. R. Willis, “Organic Electroluminescent Devices: Enhanced Carrier Injection Using SAM Derivatized ITO Electrodes,” Journal of Materials Chemistry, Vol. 10, No. 1, 2000, pp. 169-173. doi:10.1039/a903708j

NOTES

*Corresponding author.

Journal Menu >>