Journal of Sensor Technology
Vol.2 No.4(2012), Article ID:25486,5 pages DOI:10.4236/jst.2012.24024
Effect of Modulation Error on All Optical Fiber Current Transformers
Science School, Harbin Engineering University, Harbin, China
Email: zpwang@hrbeu.edu.cn
Received September 14, 2012; revised October 16, 2012; accepted November 17, 2012
Keywords: Electronic Current Transformer; All Optical Fiber Current Transformer; Faraday Effect; Active Modulation; Modulation Error
ABSTRACT
For actively modulated In-line Sagnac interferential all optic fiber current transformers (AOFCTs), the accuracies are directly affected by the amplitude of the modulation signal. In order to deeply undertand the function of the modulator, a theoretical model of modulation effect to AOFCTs is built up in this paper. The effect of the amplitude of the modulation signal to the output intensity of AOFCTs is theoretically formulated and numerical calculated. The results show that the modulation voltage variation could affect the output accuracies significantly. This might be some references on the investigation for practical applications of AOFCTs.
1. Introduction
At present, Electronic Current Transformers (ECTs) are widely used in power systems. Comparing with other kinds of ECTs, all optical fiber current transformers (AO FCTs) have been considered mainly for applications in high, ultra high, even high voltages substations. Most of reported articles about AOFCTs were based on the theory and technology of fiber optic gyroscope [1,2]. Ordinary Sagnac type interferometers have received considerable attention for optical fiber current transforming, because of their advantages [3-6] such as: optical fiber loop is located in high voltage area (without any electronic component), so it is easy to solve the problems like high-voltage partial discharge, insulation problems and electromagnetic shielding effectiveness. Moreover, in the high voltage area the elements of AOFCT are small and light [7-8]. In-line configuration [9], which is a kind of improved Sagnac interferometer, is two times more sensitive than that of Sagnac loop, substantially reduces the sensitivity to mechanical and thermal disturbances of the leading fibers, and exhibits accurate behavior in current measurement. Some major error sources of AOFCTs like temperature and mechanical perturbations, imperfect quarter wave plate, shot noise, performance of scale factor and residual fiber birefringence have already been well discussed [10-15].
According to the Faraday effect, the rotation of the plane of polarization is proportional to the intensity of the applied magnetic field in the direction of light propagation. The Faraday rotation angle 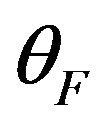 is proportional to the component of the magnetic field along the propagating direction of the light beam. For a closed optical loop, applying the Ampere’s law, the formula of the Faraday effect can be written as
is proportional to the component of the magnetic field along the propagating direction of the light beam. For a closed optical loop, applying the Ampere’s law, the formula of the Faraday effect can be written as
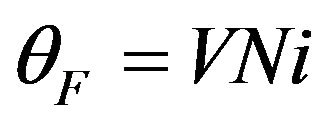 (1)
(1)
where V is the Verdet constant of the fiber, N is number of sensing coils and i is the current intensity to induce the effect. As Faraday rotation angle is very small, it may bring significant difficulties to detect the angle directly in AOFCTs without necessary phase shift. Therefore, it is necessary to add a phase modulator for easier detecting and achieving better accuracies. Accuracies of a few tenths of a percent are required for metering applications of ECT, and much better accuracies are required for certain incipient fault detection applications such as detecting the presence of leakage currents. Therefore, a careful analysis respect to modulation errors should be given to show how they affect the current transformers’ performance.
Nowadays, the reported achievements about modulation methods could divide into two groups: active modulation and passive modulation. The analysis about the effect of modulation errors of passively modulated AO FCTs was detailed in reference [16]. As to active modulation, there are two main kinds of methods, dynamic bias and static bias. Among them, the static bias will bring high instability. Usually, current transformers use dynamic bias to realize active modulation. Commonly, there are two types of dynamic bias: square-wave modulation and sine-modulation [17]. For current transformer, especially those for line protect applications, sine-modulation could much better meet the demand of responsivity.
2. Theoretical Analysis
For In-line AOFCTs, the reference frame (x, y, z) has its x and y axes at 45˚ with respect to the input linear polarization, the HiBi fiber has its birefringence axes parallel to the x and y axes and the orientation of the z axis is given by the propagation vector. The layout of an active modulation AOFCT is shown in Figure 1.
The optical vector emerging from the source can be described as E. After being launched into the fiber polarizer, the output light Ein of the polarizer, which will be lunched into the HiBi fiber delay line, can be represented by the Jones vector as
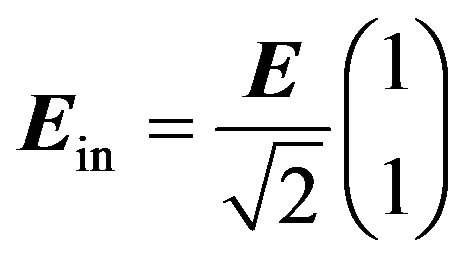 (2)
(2)
Suppose that the HiBi fiber is an ideal one, which means that no cross coupling arises from one birefringence axis to the other, the Jones matrices for forward and backward propagation of a light beam in the HiBi are the same, which could express by the Jones matrix as
 (3)
(3)
Here the right direction arrow represents forward propagation, and the left one represents backward propagation and  is the phase difference between the two modes propagating in the two principal axes of the HiBi fiber, respectively. The principal axes of a quarter wave retarder are connected at a 45˚ angle with respect to that of the HiBi fiber. The Jones matrices of the retarder can be given as
is the phase difference between the two modes propagating in the two principal axes of the HiBi fiber, respectively. The principal axes of a quarter wave retarder are connected at a 45˚ angle with respect to that of the HiBi fiber. The Jones matrices of the retarder can be given as
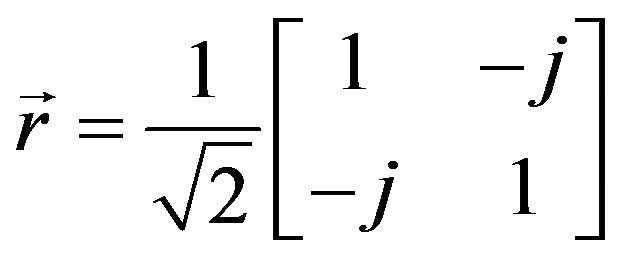 (4.1)
(4.1)
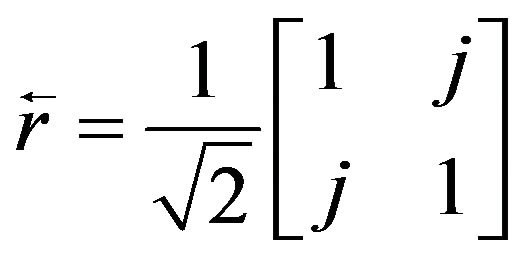 (4.2)
(4.2)
For the leading fiber, the use of highly twisted fiber can increase the circular birefringence of the fiber to quench its intrinsic linear birefringence. The circular birefringence of the leading fiber is reciprocal, hence the Jones matrices of the leading fiber for forward and backward propagation have the same form, which can be expressed as
 (5)
(5)
where  is the rotation angle induced by the highly
is the rotation angle induced by the highly
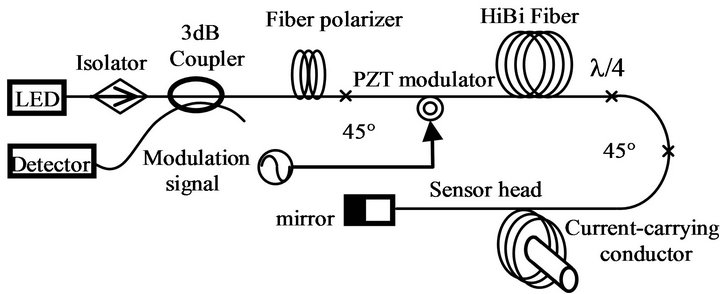
Figure 1. Layout of the AOFCTs with active modulation technique.
circular birefringence fiber.
In the sensor head part, the fiber used to compose the sensing coil is the same as the leading one. Thus they have identical Jones matrix representations. Because the Faraday effect is nonreciprocal, its induced term becomes negative for backward propagation. As the Faraday effect occurs, the induced extrinsic circular birefringence should superimpose onto the intrinsic one. So the Jones matrix representations for the sensor head could be represented as
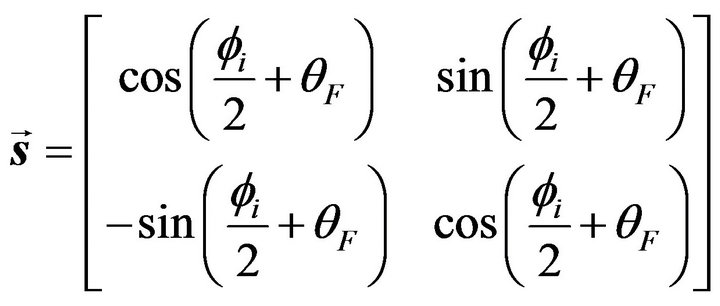 (6.1)
(6.1)
 (6.2)
(6.2)
where 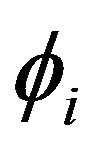 is the rotation angle in the highly twisting circular birefringence fiber.
is the rotation angle in the highly twisting circular birefringence fiber.
The mirror is represented by the Jones reflection matrix
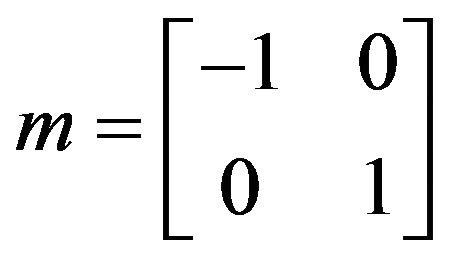 (7)
(7)
The output Eout at the connecting point between the fiber polarizer and the leading part is described as
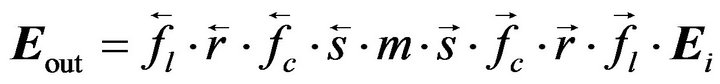 (8)
(8)
By means of Jones matrix manipulation, the result can be shown as
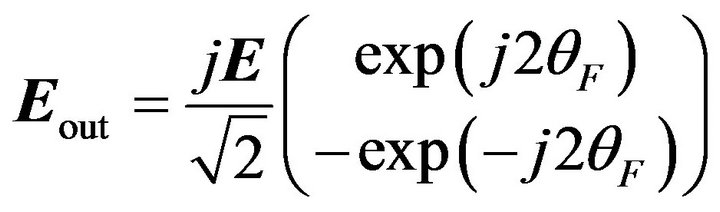 (9)
(9)
To get the interference between the two orthogonal polarizations at the output, a linear polarizer with its transmission axis aligned at 45˚ with respect to the reference axis has to be introduced.
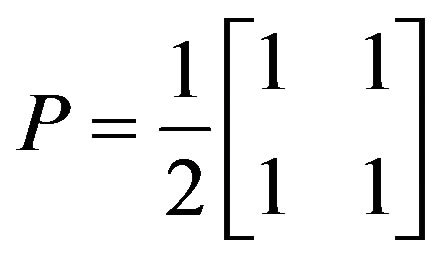 (10)
(10)
When the reflected light Eout is launched into the fiber polarizer, interference occurs. The interference Et in the output electrical field form is represented as
 (11)
(11)
Without further measures, the detected intensity resulting from the interference of the returning waves is given by
 (12)
(12)
where 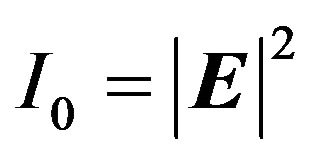 and
and 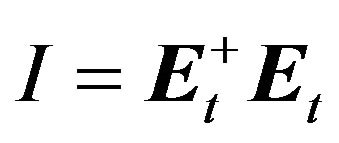 (“+” means Hermitian operators).
(“+” means Hermitian operators).
Equation (12) indicates that when the bus current intensity is very small, the detecting accuracy would be very small, because of the cosine function. Therefore, it is necessary to add a phase shift to move the working point to the most sensitive position.
PZT is one of the most widely used phase modulator. Under the control of the modulation signal u(t), the length L and refractive index n of the optical fiber wound around the PZT will correspondingly change to realize the phase modulate function. The phase variation of the fiber [18] can be written as:
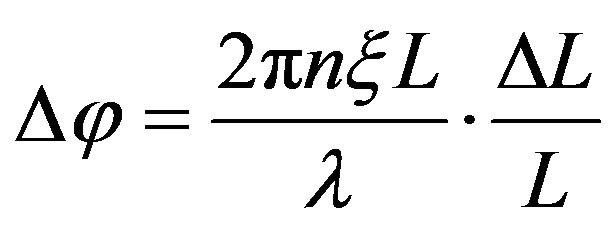 (13)
(13)
where ![]() is light wavelength in vacuum,
is light wavelength in vacuum,  is gauge factor of fiber, and
is gauge factor of fiber, and 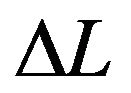 is the length variation of fiber.
is the length variation of fiber.
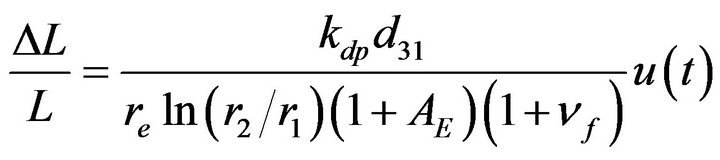 (14)
(14)
where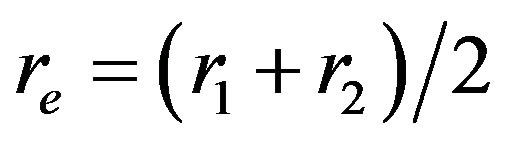 , r1 and r2 are the internal and external radius of the PZT,
, r1 and r2 are the internal and external radius of the PZT, 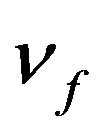 is the Poisson ratio of fiber, kdp is load coefficient, d31 is piezoelectric strain constant and AE is a constant associate with PZT material. To analyze the relationship between modulation signal and the detected output optical intensity.
is the Poisson ratio of fiber, kdp is load coefficient, d31 is piezoelectric strain constant and AE is a constant associate with PZT material. To analyze the relationship between modulation signal and the detected output optical intensity.
The phase modulation signal could be written as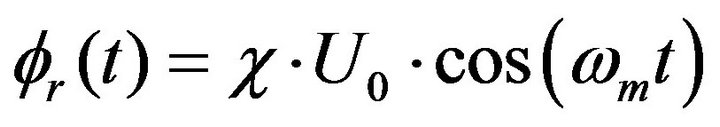 . Where U0 is the amplitude of the modulation signal and
. Where U0 is the amplitude of the modulation signal and 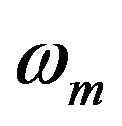 is the modulation frequency. Here it is supposed that the
is the modulation frequency. Here it is supposed that the 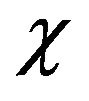 is a constant, because we are only interested in the effect of the U0, although the
is a constant, because we are only interested in the effect of the U0, although the 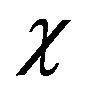 is changeable with the environment factors. Accordingly, Equation (12) become
is changeable with the environment factors. Accordingly, Equation (12) become
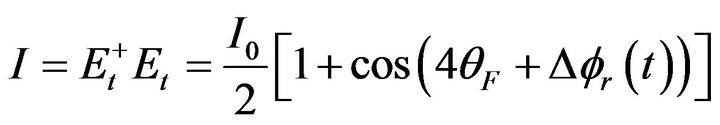 (15)
(15)
where
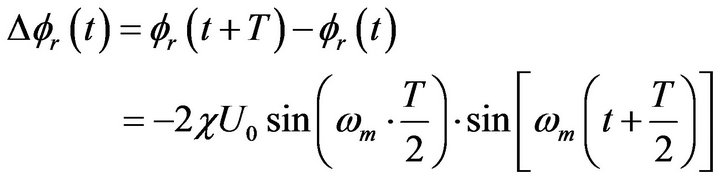
Ideally, 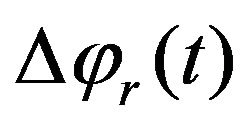 should equal to
should equal to
−p/2 (means ), but it can be seen form the equation that the amplitude of the modulation signal U0, the modulation frequency
), but it can be seen form the equation that the amplitude of the modulation signal U0, the modulation frequency  and the length of fiber L are the key factors to the output optical intensity. For a given In-line typed optical current transformer, ignoring any other influenced factor,
and the length of fiber L are the key factors to the output optical intensity. For a given In-line typed optical current transformer, ignoring any other influenced factor, 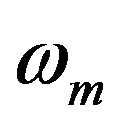 and L are fixed, so the main factor become U0.
and L are fixed, so the main factor become U0.
3. Numerical Calculation Results
To assess the effect of the amplitude of the modulation signal on the output, the transformer is assumed that all optical devices used are ideal except the modulator. And only the effect of U0 is taken into consideration. The normalized 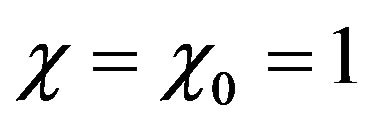 is used. Then one has
is used. Then one has
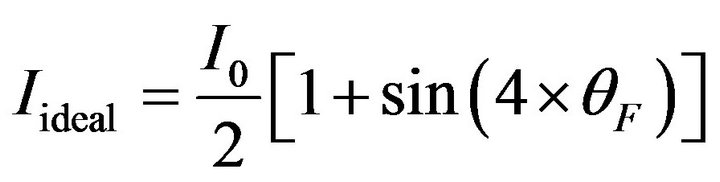
and
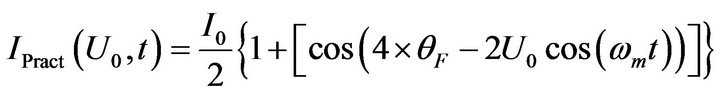
Assuming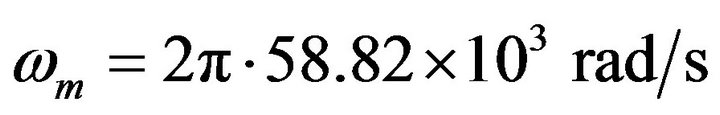 , matching the modulation frequency
, matching the modulation frequency  and the time delay
and the time delay
(means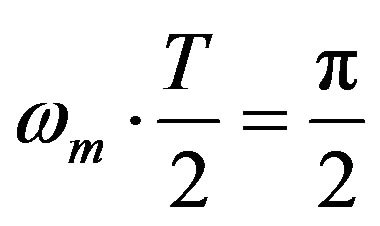 ), then L = 861 m could be obtained.
), then L = 861 m could be obtained.
Take 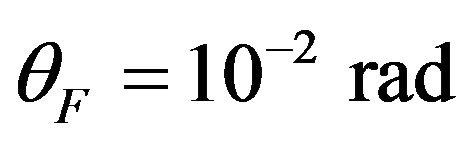 as an example, the output error of the system is defined as
as an example, the output error of the system is defined as
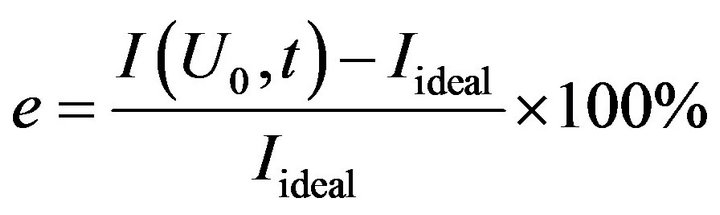 (16)
(16)
Equation (16) has its variable U0 and t. The simulation results are plotted in Figure 2 for a fixed voltage 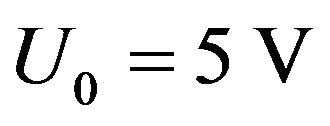 within the time interval between 20 ms and 38 ms and Figure 3 at a certain time t = 21.12 ms (when
within the time interval between 20 ms and 38 ms and Figure 3 at a certain time t = 21.12 ms (when 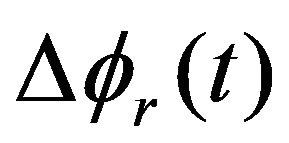 achieves –p/2 for the modulation voltage of 5 V) with the U0 ranging from 4.9 to 5.1 V.
achieves –p/2 for the modulation voltage of 5 V) with the U0 ranging from 4.9 to 5.1 V.
The pattern in Figure 2(a) is predictable form Equation (16) that the output error varies periodically with time t. Figure 2(b) shows that for a sampling process, the accuracy of the detected signal is such sensitive that different sampling time jilter may cause signficant error. Therefore, necessary technical desgn such as peak value preserving circuit should be used.
As depicted in Figures 3(a) and (b), if the magnitude of voltage shift is larger than 0.01 V from 5 V, the resulting output error would be greater than 0.2% of the ideal value and become unacceptable due to standards determined by the International Standard IEC 60044- 8:2002 [19] and the State Standard of P. R. China GB/T 20840.8-2007 [20]. Therefore, some effective and efficient methods of demodulation part of AOFCTs should be
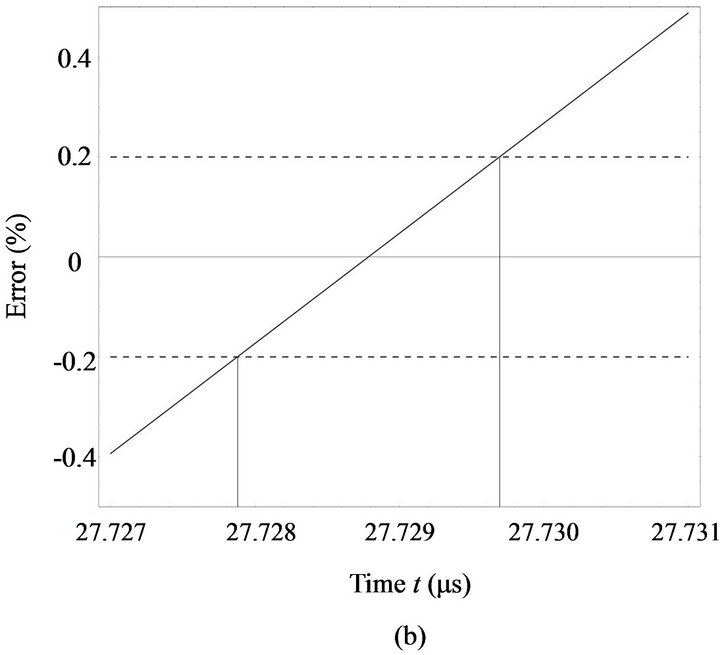
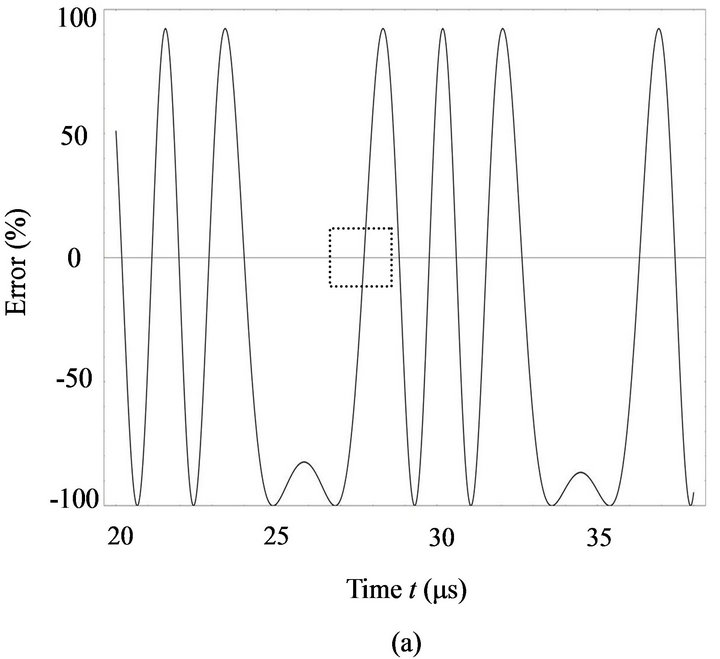
Figure 2. (a) The error for a fixed modulation voltage U0 = 5 V within the time interval between 20 s and 38 s; (b) The detailed view for the dots in the square region of (a) with parallel dash lines representing the up limit of acceptable error percentage (±0.2%, and the corresponding voltages are marked by vertical lines).


Figure 3. (a) The error induced by modulation voltage shifting from 5 V at the time t = 21.12 s; (b) The detailed view for the dots in the square region of (a). Two parallel dash lines refers to the maximum error acceptable (±0.2%). Vertical lines indicates the corresponding voltages.
carefully designed.
4. Conclusion
An analysis of modulation error associated with modulating voltage to the modulator of the AOFCTs has been calculated. The effects of the modulation voltagevariation used in the system on the performance of modulation signal to the AOFCTs have been theoretically analyzed, corresponding numerical calculation results have also been given. The results reported here indicate that even though the active modulation method has many advantages, the stability of the amplitude of modulation signal must still be taken into consideration during the design procedures for those practical applications.
REFERENCES
- L. R. Veeser and G. W. Day, “Faraday Effect Current Sensing Using a Sagnac Interferometer with a 3 × 3 Coupler,” Proceedings of the 7th Optical Fibre Sensors Conference, Sydney, 2-6 December 1990, pp. 325-328.
- K. B. Rochford, G. W. Day and P. R. Forman, “Polarization Dependence of Response Functions in 3 × 3 Sagnac Optical Fiber Current Sensors,” Journal of Lightwave Technology, Vol. 12, No. 8, 1994, pp. 1504-1509. doi:10.1109/50.317541
- M. C. Oh, J. K. Seo, K. J. Kim, H. Kim, J. W. Kim and W. S. Chu, “Optical Current Sensors Consisting of Polymeric Waveguide Components,” Journal of Lightwave Technology, Vol. 28, No. 12, 2010, pp. 1851-1857. doi:10.1109/JLT.2010.2049093
- V. H. Ortiz, J. L. Flores and G. García-Torales, “A Review on Optical Current Transducers for Power System Metering,” Proceedings of Fiber Optic Sensors and Applications V, Boston, 10-12 September 2007, p. 6770181. doi:10.1117/12.735082
- P. R. Watekar, S. Ju, S. A. Kim, S. Jeong, Y. Kim and W. T. Han, “Development of a Highly Sensitive Compact Sized Optical Fiber Current Sensor,” Optics Express, Vol. 18, No. 16, 2010, pp. 17096-17105. doi:10.1364/OE.18.017096
- I. S. Nikolay, V. R. Maksim, K. C. Yurii, P. G. Vladimir, I. S. Aleksandr, K. M. Sergey and M. K. Nikita, “Interferometric Fiber-Optic Electric Current Sensor for Industrial Application,” Key Engineering Materials, Vol. 437, 2010, pp. 314-318. doi:10.4028/www.scientific.net/KEM.437.314
- Y. N. Ning, Z. P. Wang, A. W. Palmer, K. T. V. Grattan and D. A. Jackson, “Recent Progress in Optical Current Sensing Techniques,” Review Science Instruments, Vol. 66, No. 5, 1995, pp. 3097-3111. doi:10.1063/1.1145537
- Z. P. Wang, Y. K. Wang and S. Sun, “Inquiry about All Fiber-Optic Electronic Current Transformer Technology,” Optics and Optoelectronic Technology, in press.
- J. Blake, P. Tantaswadi and R. T. Carvalho, “In-Line Sagnac Interferometer Current Sensor,” IEEE Transactions on Power Delivery, Vol. 11, No. 1, 1996, pp. 116-121. doi:10.1109/61.484007
- I. G. Clarke, “Temperature-Stable Spun Elliptical-Core Optical-Fiber Current Transducer,” Optics Letters, Vol. 18, No. 2, 1993, pp. 158-160. doi:10.1364/OL.18.000158
- J. Blake, P. Tantaswadi and R. T. de Carvalho, “In-Line Sagnac Interferometer Current Sensor,” IEEE Transactions on Power Delivery, Vol. 11, No. 1, 1996, pp. 116- 121. doi:10.1109/61.484007
- A. H. Rose, Z. B. Ren and G. W. Day, “Twisting and Annealing Optical Fiber for Current Sensors,” Journal of Lightwave Technology, Vol. 14, No. 11, 1996, pp. 2492- 2498.
- S. X. Short, J. U. de Arruda, A. A. Tselikov and J. Blake, “Stable Scale Factor Performance of an In-line Sagnac Interferometer Current Sensor,” The 12th International Conference on Optical Fiber Sensors, Washington DC, 28-31 October, 1997, pp. 100-103.
- K. Bohnert, P. Gabus, J. Nehring and H. Brändle “Temperature and Vibration Insensitive Fiber-Optic Current Sensor,” Journal of Lightwave Technology, Vol. 20, No. 2, 2002, pp. 267-276. doi:10.1109/50.983241
- R. Wüest, A. Frank, S. Wiesendanger, P. Gabus, U. E. Meier, J. Nehring and K. Bohnert, “Influence of Residual Fiber Birefringence and Temperature on the High-Current Performance of an Interferometric Fiber-Optic Current Sensor,” Conference on Optical Sensors, Prague, 20-22 April, 2009, pp. 73560K1-73560K8.
- Y. K. Wang and Z. P. Wang, “The Effect of Temperature Characteristic of Faraday Rotator to Passively Demodulated All Optical Fiber Current Transformers,” Power System Technology, in press.
- Y. X. Zhao, X. Y. Li, C. X. Liu and Y. L. Hao, “Comparative Research in Signal Processing of FOG,” Journal of Chinese Inertial Technology, Vol. 11, No. 2, 2003, pp. 52-56.
- G. Q. Liu, Z. Q. Le and D. F. Shen, “Magnetooptics,” Shanghai Science and Technology Press, Shanghai, 2001.
- International Electrotechnical Commission, International Standard IEC 60044-8, Instrument Transformers, Part 8, Electrical Current Transformers, 2002.
- General Administration of Quality Supervision, Inspection and Quarantine of the People's Republic of China and Standardization Administration of the People’s Republic of China. National Standard of People’s Republic of China, Instrument Transformers, Part 8: Electrical Current Transformers, 2007.

