Advances in Molecular Imaging
Vol.04 No.04(2014), Article ID:50842,11 pages
10.4236/ami.2014.44007
Temperature and Pressure Effects on Terahertz Time-Domain Spectroscopy of Crystalline Methedrine by Molecular Dynamics Simulation
Yu Xin, Hassan Yousefi Oderji, Ran Hai, Cailong Fu, Raja Aljarmouzi, Hongbin Ding*
School of Physics and Optical Engineering, Key Laboratory of Materials Modification by Laser, Ion and Electron Beams, Chinese Ministry of Education, Dalian University of Technology, Dalian, China
Email: *hding@dlut.edu.cn
Copyright © 2014 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 15 August 2014; revised 15 September 2014; accepted 14 October 2014
ABSTRACT
In this study, the terahertz time-domain spectroscopy (THz-TDS) of crystalline methedrine, which is one of the illegal drugs, is performed using molecular dynamics simulation by the Fourier transform of time derivative auto-correlation functions of the dipole moment. In order to accurately detect the drugs from samples, it is necessary to build a complete database for terahertz spectra under different external conditions from theoretical calculation, which are hardly obtained from the experiments directly. Our results show remarkable consistency with the available experimental data in the frequency range of 10 - 100 cm−1 indicating that the presented method has significant capability to simulate terahertz spectra at various conditions. We investigated the effects of temperature and pressure on THz-TDS by simulating the system at temperature range between 78.4 K and 400 K at pressures up to 100 atm. Results show the spectral features of THz-TDS both in intensity and profile are highly sensitive to the variation of temperature and with a lower magnitude to the variation of pressure. The vanishing, rebuilding and shifting of spectral peaks are due to the complex mechanisms such as the anharmonicity, shifting in the vibration energy levels, formation and destruction of hydrogen-binding and the deformation of the potential energy surface during the environment changing. This improved our understanding for complicated THz-TDS of crystalline methedrine and would be useful for assignment of the practical measurements.
Keywords:
Methedrine, Molecular Dynamics Simulation, Terahertz Time-Domain Spectroscopy

1. Introduction
(+)-Methamphetamine hydrochloride (known as methedrine in the trade) with the chemical formula of C10H16NCl, is a well-known synthetic stimulant selling as a kind of illegal drugs around the world. Dextrorotatory (+) enantiomer and levorotatory (−) enantiomer are two enantiomers of this compound; the former is roughly five times stronger than the latter in the pharmacological effects [1] . Therefore, the illegal production and the trade of (+)-methamphetamine hydrochloride has become a serious problem for criminal justice system in many countries [2] [3] , resulting in the need for accurately detecting and identifying methedrine inside the boxes and packages.
Although several detection methods for the illicit materials, such as using sniffer dogs or the X-ray scanners, have previously been examined, they suffer from serious restrictions; for example, canine and other trace detection methods are not so sensitive for the material inside the packages and X-ray scanners can only recognize the shape but not the type of drugs [4] . In recent years, terahertz time-domain spectroscopy (THz-TDS), an extremely attractive technique for the optoelectronics community, has been proved to be an effective means to study organic molecules and to identify some target compounds such as explosives and illicit drugs [5] . This is due to the several specific properties of the electromagnetic radiation in terahertz region. The first outstanding property is its excellent penetrability for most of the non-polar dielectric materials, such as plastic, paper, wood, cardboard and so on, which are transparent to terahertz radiation, so it can pass through the packaging cover and walls reaching the nontransparent materials inside. The second specific property, which is meaningful when it is compared with X-ray, is non-destructivity. X-ray is composed of the high energy photons, while THz radiation (T-ray) has relatively low energy photons making it safer for personnel scanning and a nondestructive evaluation tool for drug detection and inspecting other valuable samples such as antique relics [5] . THz spectroscopy has been emerging as an investigational technique to examine interesting aspects about the structure and dynamics for specific organization of intra- and intermolecular hydrogen bonds, collective motions, global nuclear motions significant in bio-molecular processes, conformations and so on [6] [7] . Additionally, interactions between THz radiation and large molecules may stimulate many resonances resulting in the THz photons being affected by characteristic amounts determined by specific interactions. As a result, abundant and valuable information of the interactions between molecules and vibration modes are contained in the absorption spectrum. Moreover, many materials exhibit characteristic spectral features which are considered “fingerprint” spectra in the THz frequency range (0.3 - 3 THz, 10 - 100 cm−1), enabling THz spectrum to be used as a particular tool to uniquely identify chemical species [8] .
When detecting the drug from samples, a complete database for the terahertz spectra of the target drug under different external conditions is necessary, while the results could not be obtained from experiments directly, since the terahertz sources are currently very expensive, and there are also some restrictions in preparing the samples of illicit drugs. That makes drug detection and identification become a challenging project recently. Hence only few reports focusing on illicit drugs, to our knowledge, have been published on experiments in this research field. This also highlights the significance of simulation methods to compensate for the lack of spectral data in the THz spectral range for the illicit drugs. Recently, Shen and co-workers experimentally studied some illicit drugs including Methamphetamine using THz-TDS and compared the results to those obtained by density functional theory (DFT) method for only a single molecule [9] -[12] . However, the weaker intermolecular bonds (such as hydrogen bond) also have strong terahertz absorptions and play an essential role in THz-TDS [13] . In this regard, Hakey et al. calculated the terahertz spectra for crystalline methedrine using solid-state density functional theory at zero temperature 1. Nevertheless, the terahertz time-domain spectroscopy, again due to the mentioned intermolecular bonds, is sensitive to the applied temperatures and pressures [14] [15] . Therefore, the simulation of THz-TDS needs an approach in which the temperature and pressure could be handled properly. Molecular dynamics (MD) simulation fits to these requirements.
Molecular dynamics simulation is a technique in which the classical equations of motion for all atoms are integrated simultaneously over a finite period of time. The resulting trajectory is then used to compute time-de- pendent properties of the system. In this work, the spectral features of solid methedrine crystal are investigated by analyzing the MD trajectories calculated under NPT ensemble at different temperatures and pressures. The results compared with the experimental are in good agreement showing that the simulation can be helpful to prepare the useful information in detection and identification of illegal drugs.
This paper is organized as follows: the next section presents the simulation details and provides the theoretical method for calculating the THz spectra. In Section 3, we compare our simulation under NPT ensemble with experimental results, and then we present the THz spectra as the functions of temperatures and pressures. Finally, we give the conclusion of our work in Section 4 indicating the potential of MD simulation approach in prediction of THz spectrum.
2. Simulation Details
The unit cell parameters of crystalline methedrine were rendered from POV-Ray [16] . The structure of (+)-Me- thamphetamine hydrochloride molecule, the unit cell that contains two molecules and the different surfaces of the supercell are shown in Figures 1(a)-(e). The hydrogen bonds are represented by dash lines. The unit cell has a space group of P21 with the lengths of a = 0.71022 nm, b = 0.72949 nm, c = 1.08121 nm, and angles of α = γ = 90˚ and β = 97.273˚. The supercell has monoclinic structure building by 5 × 5 × 5 unit cells including 7000 atoms in total.
To calculate the instantaneous dipole moments from the MD trajectories, the values of charges on each atom should be known. We used the Gaussian 03 package [17] to optimize the structure of (+)-Methamphetamine hydrochloride molecule and to determine the charge distribution on atoms of a system including four methedrine molecules using the density function theory (DFT) with 6 - 31 g (d, p) basic set at B3LYP level [18] . We used only four molecules because of the restriction in the number of atoms in the G03 software and finally we adopted the charge values from the most symmetric molecule among the 4 unique molecules of the cell. The charge values are reported in Table 1.
The MD simulation was performed with DL_POLY parallel simulation program package [19] . The force field of potential energy contributions was generated from parameter sets of Dreiding potential [20] . It has been proved that the simulation results of THz spectrum are only weakly affected by the substitute of the bonds constraints from harmonic oscillators to anharmonic oscillators [21] . For this reason, in this research, the covalent bond-stretching terms were just treated as harmonic oscillators in the force field.
In order to examine the effects of hydrogen bond interaction, we added two sets of hydrogen bond interaction parameters into force field parameters for non-bonded interactions. The interaction between donor and acceptor atom is represented by the form of 12 - 10 potential function,
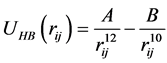 (1)
(1)
In our work, the constant A and B for H…N hydrogen bonds were obtained from [22] . While for H…Cl, the two parameters of hydrogen bond potential were not determined directly. Hence, we derived the values from the potential function which was shown to empirically describe linear hydrogen bonds properties [23] . The obtained potential parameters A and B for hydrogen bonds H…N and H…Cl are listed in Table 2.
In molecular dynamics simulation, we introduced periodic boundary conditions in all three directions. The velocity-Verlet algorithm was applied for integrating the equations of motion. The cut-off radii for electrostatic interactions and van der Waals interactions were set to 1 nm. Equilibrations with 20 ps were followed by pro-


Figure 1. One single molecule of (+)-Methamphetamine hydrochloride (a); the unit cell of crystalline methedrine (b); the projection for ab plane (c); bc plane (d) and ac plane (e).
Table 1. The electronic charge values of each atom in one methedrine molecule.
Table 2. Parameters for the 12 - 10 potential between hydrogen H and acceptor atoms.
duction runs of 100 ps using a time step of 0.1 fs. The SHAKE [24] algorithm was used during the whole simulation to constrain all the bond distances.
After obtaining the trajectory from MD simulation, the terahertz spectrum can be computed via the Fourier transform of the time auto-correlation function of the total dipole moment M of the system [25] ,
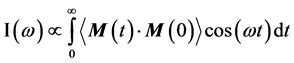 (2)
(2)
where I(ω) is the absorption line intensity, 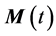 is the dipole moment operator and the bracket denotes the ensemble average.
is the dipole moment operator and the bracket denotes the ensemble average.
Decaying to zero is an obligatory condition for integrability of Equation (2). This condition easily establishes for the gases and liquids, due to randomly motions of molecules in fluid, however, in solids, with only atomic vibration, dipole moment values decays slowly, which is beyond the time scales capable by MD. For solids, it is proved that the calculation of I(ω) from the time derivative of auto-correlation function prepare a better way to obtain the terahertz spectrum [26] .
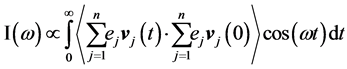 (3)
(3)
The auto-correlation function of the dipole moment is given by [26] -[28] ,
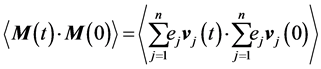 (4)
(4)
where ej is the charge of the jth atom, and rj(t) is the position vector of the jth atom at time t.
And the derivative is given as,
 (5)
(5)
Figure 2 shows, the time derivative auto-correlation function of the methedrine solid system decaying rapidly to zero. Due to the fluctuation around the value of zero for much a long time, a Gaussian type term exp(-αt2) was introduced to suppress the fluctuations of the dipole moment auto-correlation functions.
Therefore, the spectral density in this work was calculated as [26] ,
 (6)
(6)
The parameter α in Equation (6) determines the resolution for the frequencies of the vibrational spectrum. If one chose the parameter to be too large, the overlap between the close peaks occurs. Conversely, some unreal peaks would be calculated from the fluctuations. In Figure 3, the comparison between the calculated spectra using the different α values of 0.01, 0.04, and 1.00 is shown. In this work, we used α = 0.04 that provides reasonable comparison between the experimental and calculated results.
The absorption of light by crystals depends on the angle between the irradiated beam and the target surface. Hence as it can be seen in Figure 4, the absorption in x, y and z directions are different. Averaging on all direc-
Figure 2. The calculated time derivative auto-correlation function.
Figure 3. Comparison between the calculated spectra using different α values 0.01, 0.04, and 1.00.
Figure 4. Calculated results of x, y and z directions, and the averaged spectrum.
tions reasonably reproduced the conditions in available experiments, the spectral experimental detection [12] in which the samples are composed from fine particles.
3. Results and Discussions
Firstly, the spectra of methedrine at temperature of 78.4 K and 294 K at constant pressure of 1 atm (atmosphere) were simulated using Berendson NPT ensemble [29] with the relaxation time of 0.5 ps for both thermostat and barostat. By performing molecular dynamics simulations in NPT ensemble, the volume and the density of system are allowed to change and the pressure and temperature are kept constant. Hence, this ensemble provides the ability to control the temperature and pressure as it is usually desired to do experiments. The calculated peaks in terahertz spectra and the experimental results from [1] are reported in Table 3. In addition, Figure 5 presents a graphically comparison between the experimental and calculated spectra. The comparison shows that the calculated values are in good agreement with the experimental results within ±4 cm−1 for the calculation at 78.4 K. The detection of peaks in terahertz spectroscopy depends on the resolution and the quality of the experimental instruments and the methods. While in the experiment by Li et al. [12] a total of four spectral absorptions were noted, a fifth one was reported by Kanamori et al. [30] and two additional features were identified by Hakey et al. [1] . Here, simulations predict even more four features at temperature of 78.4 K, three peaks at frequencies lower than 44 cm−1 and another one at 66.933 cm−1. At this temperature, simulations also present that the experimental peak at 73.290 cm−1 could be regarded as an overlap of two sharper peaks at 71.262 cm−1 and 76.590 cm−1. Similarly, the peak of 85.153 cm−1 in experiment could also be the superposition of two peaks of 80.253 cm−1 and 87.246 cm−1 in simulation. Hence, accounting for the simulation results, the total number of spectral absorptions for methedrine reaches to 13 at temperature of 78.4 K. This situation is even more pronounced for the simulations under the higher temperature of 294 K at which the total number of spectral absorptions predicted by simulations reaches to 14. At this temperature, calculated spectral absorptions are even with a better agreement with the experimental results (±3 cm−1) in comparison to the lower temperature of 78.4 K. Even at low frequency (within 40 cm−1), we have calculated five peaks which are hardly detected by experiment. Similar to the peaks at 73.290 cm−1 and 85.153 cm−1 for the simulation at 78.4 K, the absorption at 60.875 cm−1 detected by the experiments can be interpreted as a superposition of the peaks at 57.942 cm−1 and 62.271 cm−1 obtained from simulations.
To investigate the effect of temperature on the THz absorption of methedrine, we also simulated the changes of spectra with temperatures at constant pressure. The calculated THz spectra of crystalline methedrine in the range of 10 - 100 cm−1 are presented in Figure 6, at the constant pressure of 1 atm and at different temperatures of 78.4 K, 100 K, 294 K and 400 K. As a general trend, Figure 6 shows that the intensities of the frequencies lower than 45 cm−1 are less than the intensities of the higher frequencies. The intensities of frequencies at this region mostly increase with temperature. This effect can be easily seen from the temperature profile at frequency of 10 cm−1 in Figure 6 at which the intensity at 400 K is twice in magnitude of the intensity at 78.4 K. However,
Figure 5. Comparison between the experiment and simulation spectra under NPT ensemble of methedrine with the temperature of 78.4 K (a) and 294 K (b).
Figure 6. Simulated THz spectra of methedrine at constant pressure of 1 atm and different temperatures of 78.4 K, 100 K, 294 K and 400 K.
the peaks at frequencies higher than 45 cm−1 do not exhibit a monotonic behavior by the increasing of temperature. For example, the absorption intensity of 78.255 cm−1 at temperature of 100 K is stronger than that of the same frequency at other temperatures. Similarly, comparing with other temperatures, the vibrations with frequencies of 62.604 cm−1 and 87.246 cm−1 at low temperature of 78.4 K occur with high intensities. We also collected the values of spectral peaks in Table 4, presenting 13 peaks at 78.4 K, 11 peaks at 100 K, 14 peaks at 294 K and 11 peaks at 400 K. The table shows that increasing the temperature can effect on the peaks not only by shifting frequencies slightly to lower or higher frequencies, but also it can completely change the mode of vibration. It can be explained by considering the nature of the features at terahertz region in which originates from the weak bonds between the molecules. Increasing the temperature can considerably change the configuration of molecules within the crystal (or equivalently the shape of potential energy surface), leading to the interferer of farther atoms belonging to other molecules and creating new vibrational modes. We take the peak of 19.980 cm−1 at 78.4 K as an example (19.980 cm−1 at 78.4 K, 17.316 cm−1 at 100 K and 16.650 cm−1 at 400 K); it is thought that the peak should move to lower frequency with the increasing temperature. The peak at 19.980 cm−1, however, appears again at T = 294 K. This situation also happens to the peak 57.942 cm−1 existing at both 100 K and 294 K and the peak 66.933 cm−1 existing at both 78.4 K and 294 K. This may be due to the breaking and rebuilding of weak interactions such as hydrogen bond. At some temperatures, the atoms in the new configuration may not be close enough to make interactions or binding, so some corresponding vibrational frequencies may be vanished. However, some peaks can be seen at all the temperatures indicating that they are belonging to the stronger covalent bonds, for example, the peaks around 43 cm−1, 53 cm−1, 82 cm−1 and 88 cm−1. Moreover,
Table 3. The spectral peaks of experiment and simulation spectra of methedrine with the temperature of 78.4K and 294K. (Experiment data are from [1] ).
Table 4. The calculated spectral peaks of methedrine at temperature of 78.4 K, 100 K, 294 K and 400 K at pressure of 1 atm.
some peaks show the blue shift while some others show the red shift. For example, the peak of 41.292 cm−1 at 78.4 K presents an obvious blue shift, while the peak of 27.972 cm−1 at 100 K shifts to lower frequencies by increasing the temperature.
The effect of pressure on the peak positions and intensities was investigated by simulating the systems at constant temperature of 78.4 K under the different pressures of 1, 2, 10 and 100 atm, presented in Figure 7. This figure shows that the effect of pressure on the THz-TDS is not as strong as the effect of temperature. However, this effect is also considerable. At the constant temperature of 78.4 K and under every pressure, the absorption begins from the frequency of 25 cm−1 and shows two outstanding regions of 60 - 75 cm−1 and 80 - 100 cm−1. The absorption intensities of the vibrations with very low frequency (below 20 cm−1) are almost zero at different pressures. The highest absorption intensities at peaks of 43.956 cm−1, 55.611 cm−1, 80.919 cm−1 and 87.246 cm−1 are obtained under the pressure of 10 atm while the highest intensity for the peaks at 64.935 cm−1 and 92.974 cm−1 can be obtained by applying 100 atm of pressure. The values of spectral peaks are also collected in Table 5.
Figure 7. Simulated THz spectra of methedrine at constant temperature of 78.4 K and different pressures of 1 atm, 2 atm, 10 atm and 100 atm.
Table 5. The calculated spectral peaks of methedrine with the temperature of 1 atm, 2 atm, 10 atm and 100 atm at temperature of 78.4 K.
There are 13, 12, 10 and 11 peaks at the pressure of 1, 2, 10 and 100 atm, respectively. Similar to what occurs due to the increasing of temperature, some peaks are vanished and again appeared by increasing the pressure; some of them show a blue shift and some a red shift. There is no constant trend for the THz-TDS by increasing the pressure. The reason for this complex behavior, similarly to the case of variation of the temperature, mostly refers to the configuration deformation caused by the pressure which in turn changes the potential energy surface. We note that if there was no change for the configuration or potential energy surface, increasing the temperature would shift the peaks to lower frequencies due to the anharmonicity. At high temperatures system mostly populates at the high-energy levels. However, due to the anharmonicity the high-energy levels are much closer than the lower ones. Therefore, the vibrational transitions need the photons with lower energies (or lower frequencies). As a results, increasing the temperature leads to the increasing of the absorption at lower frequencies. In contrast, increasing the pressure increases the energy gaps between the energy levels resulting in increasing the energy of photon required to excitation. This in turn shifts the frequencies to higher values.
4. Conclusion
Variation of the absorption THz spectra of crystalline methedrine with the change of temperature and pressure was investigated by molecular dynamics simulations for the first time. Dreiding potential was used to model the covalent bonds and the hydrogen bonds were modeled by 12 - 10 potential function. The absorption line intensities were calculated using the time derivative of the auto-correlation functions of the dipole moment. The results were compared with the available experimental data and indicated a reasonable agreement within at most ±4 cm−1 at T = 78.4 K and ±3 cm−1 at T = 294 K. In addition, we examined the positions and intensities variation of methedrine terahertz spectra at the different temperatures of 78.4 K, 100 K, 294 K, 400 K and the different pressures of 1 atm, 2 atm, 10 atm, 100 atm in the frequency range of 10 - 100 cm−1. The results showed that the THz-TDS of crystalline methedrine is very sensitive to the temperature and pressure. The effects were found to be very complex showing the red shift for some peaks and blue shift for some other peaks as well as the occasionally vanishing some peaks and appearing new ones. These complex behaviors were explained to be related to the anharmonicity, increasing the gap between the energy levels, destruction and building of the weak interactions and the deformation of the potential energy surface, respectively. Based on the features of positions and intensities of methedrine terahertz absorption spectra, it is proved to possibly detect and identify the samples under the different temperatures and pressures. This work helps to deeply understand the crystal properties, population and distribution of molecular vibrational and hydrogen bonding depending on variation of applied conditions. Moreover, our results in conclusion provide a database for identifying the drugs from samples and demonstrate the importance of controlling the ambient pressure and temperature in detection of crystalline methedrine using THz-TDS technique.
Acknowledgements
This work has been supported by the Fundamental Research Funds for the Central Universities (Nos. DUT12ZD (G)01) and the National Natural Science Foundation of China (Nos. 11175035).
References
- Cho, A.K. (1990) Ice: A New Dosage form of an Old Drug. Science, 249, 631-634. http://dx.doi.org/10.1126/science.249.4969.631
- Hakey, P.M., Allis, D.G., Ouellette, W. and Korter, T.M. (2009) Cryogenic Terahertz Spectrum of (+)-Methampheta- mine Hydrochloride and Assignment. Journal of Physical Chemistry A, 113, 5119-5127. http://dx.doi.org/10.1021/jp810255e
- Tubergen, M.J., Lavrich, R.J., Plusquellic, D.F. and Suenram, R.D. (2006) Rotational Spectra and Conformational Structures of 1-Phenyl-2-propanol, Methamphetamine, and 1-Phenyl-2-propanone. Journal of Physical Chemistry A, 110, 13188-13194. http://dx.doi.org/10.1021/jp064810u
- Neutze, R., Wouts, R., van der Spoel, D., Weckert, E. and Hajdu, J. (2000) Potential for Biomolecular Imaging with Femtosecond X-Ray Pulses. Nature, 406, 752-757. http://dx.doi.org/10.1038/35021099
- Davies, A.G., Burnett, A.D., Fan, W., Linfield, E.H. and Cunningham, J.E. (2008) Terahertz Spectroscopy of Explosives and Drugs. Materials Today, 11, 18-26. http://dx.doi.org/10.1016/S1369-7021(08)70016-6
- Walther, M., Fischer, B.M. and Uhd Jepsen, P. (2003) Noncovalent Intermolecular Forces in Polycrystalline and Amorphous Saccharides in the Far Infrared. Chemical Physics, 288, 261-268. http://dx.doi.org/10.1016/S0301-0104(03)00031-4
- Allis, D.G., Fedor, A.M., Korter, T.M., Bjarnason, J.E. and Brown, E.R. (2007) Assignment of the Lowest-Lying THz Absorption Signatures in Biotin and Lactose Monohydrate by Solid-State Density Functional Theory. Chemical Physics Letters, 440, 203-209. http://dx.doi.org/10.1016/j.cplett.2007.04.032
- Ge, M., Wang, W., Zhao, H., Zhang, Z., Yu, X. and Li, W. (2007) Characterization of Crystal Transformation in the Solid-State by Terahertz Time-Domain Spectroscopy. Chemical Physics Letters, 444, 355-358. http://dx.doi.org/10.1016/j.cplett.2007.07.028
- Sun, J., Shen, J., Liang, L., Xu, X., Liu, H. and Zhang, C. (2005) Experimental Investigation on Terahertz Spectra of Amphetamine Type Stimulants. Chinese Physics Letters, 22, 3176-3178. http://dx.doi.org/10.1088/0256-307X/22/12/054
- Wang, G., Shen, J. and Jia, Y. (2007) Vibrational Spectra of Ketamine Hydrochloride and 3, 4-Methylenedioxyme- thamphetamine in Terahertz range. Journal of Applied Physics, 102, Article ID: 013106. http://dx.doi.org/10.1063/1.2752139
- Deng, F., Shen, J., Wang, G. and Liang, M. (2008) Spectroscopy Study of Ephedrine Hydrochloride and Papaverine Hydrochloride in Terahertz Range. 2008 International Conference on Optical Instruments and Technology: Microelectronic and Optoelectronic Devices and Integration, 2008, 71580S.
- Li, N., Shen, J., Sun, J., Liang, L., Xu, X., Lu, M. and Yan, J. (2005) Study on the THz Spectrum of Methamphetamine. Optics Express, 13, 6750-6755. http://dx.doi.org/10.1364/OPEX.13.006750
- Agarwal, V., Huber, G.W., Conner, W.C. and Auerbach, S.M. (2011) Simulating Infrared Spectra and Hydrogen Bon- ding in Cellulose Iβ at Elevated Temperatures. Journal of Chemical Physics, 135, Article ID: 134506. http://dx.doi.org/10.1063/1.3646306
- Olejniczak, I. and Pogorzelec-Glaser, K. (2012) Lattice Dynamics through the Structural Phase Transition in D-Am- phetamine Sulfate. Journal of Physical Chemistry A, 116, 9854-9862. http://dx.doi.org/10.1021/jp304843g
- Walther, M., Plochocka, P., Fischer, B., Helm, H. and Jepsen, P.U. (2002) Collective Vibrational Modes in Biological Molecules Investigated by Terahertz Time-Domain Spectroscopy. Biopolymers, 67, 310-313. http://dx.doi.org/10.1002/bip.10106
- Hakey, P., Ouellette, W., Zubieta, J. and Korter, T. (2008) Redetermination of (+)-Methamphetamine Hydrochloride at 90 K. Acta Crystallographica Section E: Structure Reports Online, 64, o940. http://dx.doi.org/10.1107/S1600536808011550
- Frisch, M., Trucks, G., Schlegel, H., Scuseria, G., Robb, M., Cheeseman, J., Montgomery, J., Vreven, T., Kudin, K. and Burant, J. (2008) Gaussian 03, Revision C. 02.
- Lee, C., Yang, W. and Parr, R.G. (1988) Development of the Colle-Salvetti Correlation-Energy Formula into a Functional of the Electron Density. Physical Review B, 37, 785. http://dx.doi.org/10.1103/PhysRevB.37.785
- Smith, W. and Forester, T.R. (1996) DL_POLY_2.0: A General-Purpose Parallel Molecular Dynamics Simulation Pa- ckage. Journal of Molecular Graphics, 14, 136-141. http://dx.doi.org/10.1016/S0263-7855(96)00043-4
- Mayo, S.L., Olafson, B.D. and Goddard, W.A. (1990) DREIDING: A Generic Force Field for Molecular Simulations. Journal of Physical Chemistry, 94, 8897-8909. http://dx.doi.org/10.1021/j100389a010
- Pereverzev, A. and Sewell, T.D. (2011) Terahertz Spectrum and Normal-Mode Relaxation in Pentaerythritol Tetranitrate: Effect of Changes in Bond-Stretching Force-Field Terms. Journal of Chemical Physics, 134, Article ID: 244502. http://dx.doi.org/10.1021/j100234a011
- Nemethy, G., Pottle, M.S. and Scheraga, H.A. (1983) Energy Parameters in Polypeptides. 9. Updating of Geometrical Parameters, Nonbonded Interactions, and Hydrogen Bond Interactions for the Naturally Occurring Amino Acids. Jour- nal of Physical Chemistry, 87, 1883-1887. http://dx.doi.org/10.1021/j100234a011
- Schroeder, R. and Lippincott, E.R. (1957) Potential Function Model of Hydrogen Bonds. II. Journal of Physical Chemistry, 61, 921-928. http://dx.doi.org/10.1016/0021-9991(77)90098-5
- Ryckaert, J.P., Ciccotti, G. and Berendsen, H.J. (1977) Numerical Integration of the Cartesian Equations of Motion of a System with Constraints: Molecular Dynamics of n-Alkanes. Journal of Computational Physics, 23, 327-341. http://dx.doi.org/10.1016/0021-9991(77)90098-5
- McQuarrie, D.A. (2000) Statistical Mechanics. Sausalito.
- Praprotnik, M., Janežič, D. and Mavri, J. (2004) Temperature Dependence of Water Vibrational Spectrum: A Molecular Dynamics Simulation Study. Journal of Physical Chemistry A, 108, 11056-11062. http://dx.doi.org/10.1021/jp046158d
- Bornhauser, P. and Bougeard, D. (2001) Intensities of the Vibrational Spectra of Siliceous Zeolites by Molecular Dynamics Calculations. I. Infrared Spectra. Journal of Physical Chemistry B, 105, 36-41. http://dx.doi.org/10.1021/jp0014925
- Bren, U. and Janežič, D.A. (2012) Individual Degrees of Freedom and the Solvation Properties of Water. Journal of Chemical Physics, 137, Article ID: 024108. http://dx.doi.org/10.1063/1.4732514
- Berendsen, H.J., Postma, J.P.M., van Gunsteren, W.F., DiNola, A. and Haak, J. (1984) Molecular Dynamics with Cou- pling to an External Bath. Journal of Chemical Physics, 81, 3684. http://dx.doi.org/10.1063/1.448118
- Kanamori, T., Tsujikawa, K., Iwata, Y.T., Inoue, H., Ohtsuru, O., Kishi, T., Hoshina, H., Otani, C. and Kawase, K. (2005) Application of Terahertz Spectroscopy to Abused Drug Analysis. The Joint 30th International Conference on Infrared and Millimeter Waves and 13th International Conference on Terahertz Electronics, 1, 180-181.
NOTES
*Corresponding author.










