Advances in Chemical Engineering and Science
Vol.06 No.01(2016), Article ID:62677,9 pages
10.4236/aces.2016.61002
A Convective Thin Layer Drying Model with Shrinkage for Kent Mango Slices
Alfa Oumar Dissa1*, Hélène Desmorieux2, Jean Koulidiati1
1Laboratoire de Physique et de Chimie de l’Environnement (LPCE), Unité de Formation et de Recherche en Sciences Exactes et Appliquée (UFR/SEA), Université de Ouagadougou, Ouagadougou, Burkina Faso
2Laboratoire d’Automatisme et de Génie des Procédés (LAGEP), UCBL1-CNRS UMR 5007-CPE Lyon, Université Claude Bernard Lyon 1, Lyon, France
Copyright © 2016 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 7 November 2015; accepted 9 January 2016; published 12 January 2016
ABSTRACT
In this work, a model of convective drying of mango slices was developed and validated by experiments. This model was established by considering slices shrinkage in the energy and the mass balances during the thin layer drying. The drying kinetics and the temperature curves of the product were simulated using the model at various drying temperatures. The simulated curves were then compared to the experimental curves obtained using a convective dryer controlled in temperature and moisture. The results showed that the drying curves were suitably fitted by the thin layer drying model with a correlation coefficient r2 = 0.997. Thus, taking shrinkage into account, it is possible to predict more effectively the thin layer drying kinetics of mango slices. This study therefore contributed to the mango drying modelling and to the mango dryer setting.
Keywords:
Convective Drying, Mango, Modelling, Thin Layer, Kinetic

1. Introduction
The dried mango occupies a great part of dried fruit export from West Africa. For example, in Burkina Faso, the seasonal production of mango is about 47,600 to 54,000 tons and its export has gone up from 602.1 to 4921.2 tons respectively from 1992 to 2005 [1] . In spite of the increase in these exports, great quantities of mango fruit (about 50% of the national production) are perishing under trees each season because of the lack of suitably designed dryers. In the case of mango fruit, the drying method commonly used in industry and traditionally is convective drying and the drying process is generally carried out in thin layer. Therefore, the modelling of convective thin layer drying of mango slices is necessary for a better control of the drying process and for having dried fruits of good quality respecting the standards of importing countries. It is within this framework that this work takes place. Few studies were undertaken, in the literature on convective mango drying: Dissa, Demorieux, Bathiebo & Koulidiati [2] studied the convective drying characteristics of Amelie mango (Mangifera indica L. cv. “Amelie”) by taking shrinkage into account in drying data processing. Dissa, Bathiebo, Kam, Savadogo, Desmorieux & Koulidiati [3] modelled and experimented thin layer indirect solar drying of Amelie mango slices. By experimenting a solar with natural convective heat flow, Gbaha et al. [4] studied the direct solar drying kinetics of plantain banana, sweet banana, cassava and mango. Madlopa, Jones & Kalenga [5] studied the indirect solar drying of mango slices using a natural convection solar dryer with a composite-absorber system. Touré and Kibangu-Nkembo [6] studied the free convection sun-drying of cassava, banana and mango. Majority of these works did not deal with the modelling of thin layer convective drying of mango slices whereas this drying process is the most used. Thus, the aim of this work is to propose a convective drying model which suitably describes the drying kinetic of mango slices in thin layer. This study therefore contributes to the setting of thin layer convective dryer of mango.
2. Materials and Methods
2.1. Mango Samples
The Kent variety used in this study was purchased from a local fruit market of Bobo Dioulasso, town in the west of Burkina Faso. At their arrival to the laboratory, the measures were made on the fruits between the first and seventh day. For measures, good quality fruits were selected and washed into water to which a small quantity of Natrium hypochlorite was added as disinfectant, rinsed with drinking water and peeled. The pulp was separated from the stone and sliced through according to the desired thickness.
2.2. Drying Experiments
Drying kinetics of Kent mango slices were established from samples mass loss kinetics using a laboratory mechanical convection oven dryer with digital controller (universal MEMMERT UFP 600 256L 30˚C - 250˚C) (Figure 1). The drying system allowed controlling temperature and the velocity of drying air. The air velocity is given in percentage of maximal velocity. This maximal velocity was previously measured by an anemometer TESTO 425 (resolution: 0.01 m/s for 0 to 20 m/s). The relative humidity in dryer was measured by digital probe thermohygrometer TESTO 635 (resolution: 0.1% for 0% to 100% RH). Mass measurements according to drying time were carried out at three temperatures (50˚C, 60˚C, and 70˚C) for samples of 5 mm thick. This thickness was the average value of mango slices initial thickness used in dryers in Burkina Faso. To obtain this desired
Figure 1. The experimental dryer set-up: 1―mango sample; 2―thermocouple for sample temperatures; 3―temperature data recorder; 4―heater (electrical resistance); 5―fan for force convection; 6― balance for sample weighing; 7―computer for data recording and processing.
thickness, the samples thickness were measured using a micrometer Mitutoyo (Japan) of 2 × 10−5 meter precision at the beginning of the drying. At the end of the drying experiment, the dry mass was evaluated by drying the final sample in an oven-dryer (MEMMERT) at 70˚C for 24 h [7] . From mass loss curves and dry mass, moisture content at each instant of drying and drying kinetics were determined.
2.3. Shrinkage Measurement
The shrinkage curves of Kent mango were established at 40˚C, 50˚C, 60˚C and 70˚C by using parallelepipedic shape samples. The initial dimensions of these samples were presented in Table 1. For shrinkage measurements, the mango slices were dried at 40˚C, 50˚C, 60˚C or 70˚C in an oven-dryer (WTF BINDER). During drying, the dimensions of slices were measured using a micrometer Mitutoyo (Japan) of 2 × 10−5 meter precision. These measurements were done every 10 min during the first 110 min, then every 15 min until 300 min drying and finally every 30 min until the end of drying determined by constant weight. The dimensions were measured at several places of the mango samples and only their mean values were considered.
Although the sizes changes due to the great water loss during the drying process, it was noticed that the initial shape of the slices was approximately conserved. The results of shrinkage measurements obtained were the means of three trials at every temperature. The volume of the sample at each instant of the drying was thus calculated as length × width × thickness. The shrinkage coefficient was then deduced from experimental data according to the following formula:
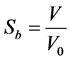 (1)
(1)
where V is the sample volume at an instant of the drying and V0 its initial volume.
During the drying process, the weight of the sample was regularly measured with a balance (SARTORIUS, 0.001 g precision, France). For each measure, the corresponding weights were noted. An oven-dryer and a balance (SARTORIUS, France) of 0.001 g precision were used to determine samples moisture content. At the end of the drying experiment, the dry mass was evaluated by drying the final sample in an oven-dryer (MEMMERT) at 70˚C for 24 h [7] . Changes in Sb with respect to the moisture content (reported to its initial value) constitute the shrinkage curve. The experimental shrinkage curves obtained were then simulated with a linear model of volume additivity.
2.4. Desorption Isotherm Establishment
Isotherm of Kent mango was established at 40˚C using an activimeter, FA-st (Food Analysis Science and Technology GBX, France) with activity precision of ±0.003. The temperature of this activimeter was regulated by circulating of water under the samples. The pieces of mangoes used in the activimeter were from 14 mangoes. The activimeter was limited by a maximal temperature of 40˚C and did not allowed to obtain desorption isotherms for higher drying air temperatures. A modified Henderson model of isotherms was then used to take drying temperature variation into account. The use of the parameters of this model for the whole drying air temperature range was motivated by the results of Myara and Sablani’s works [8] which showed that mango isotherm does not vary much with temperature in 15˚C to 60˚C range. The experiences were carried out three times to check the repeatability. To prepare samples, the two cheeks of each fruit used were removed and shared into about 5 mm thick slices of about 12 g each. All the pieces were placed at 60˚C in an oven dryer (WTF BINDER, Germany). As drying progressed, a portion of mango was retrieved from the oven at regular time intervals,
Table 1. Characteristic of samples used for shrinkage measurement.
chopped into tiny pieces to facilitate the transfer, and then placed in the cupel of the activimeter. The activimeter records the air dew temperature around the product, when equilibrium is reached between the product and the air. From this measurement and that of the dry temperature of air, the relative humidity of air is deducted. At equilibrium, this relative humidity of air equals the water activity of the product [1] . The equilibrium moisture content Xeq, corresponding to the air relative humidity was determined by drying the final sample in an oven-dryer (MEMMERT) at 70˚C for 24 h [7] .
3. Drying Model Formulation
In fruits with high initial water content such as mango, the volume of shrinkage is almost equal to the volume of water loss by dehydration [1] . The shrinkage is then close to an ideal shrinking where the decrease of material volume is exactly equal to the volume of removed liquid. In this case, both heat and mass transfer phenomena are strongly affected by the material deformation and it is essential to take shrinkage into account in the drying modelling. Therefore, the thin layer drying of Kent mango was studied by coupling drying and shrinkage processes.
3.1. Model of Shrinkage
In this current study, the shrinkage was taken into account both in drying rates and mass and energy balances through the surface area shrinkage. The model of shrinkage used is based on the hypothesis of the additivity of volumes of water and solids, assuming that the volume of air in pores is negligible and that cellular tissues are incompressible. Thus, the volume versus the moisture content (on dry basic) X of the product can be expressed as:
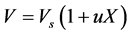 (2)
(2)
where: rs is the density of solid matrix and rw the density of water.
Then, the shrinkage coefficient can be stated as:
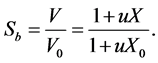 (3)
(3)
Then the surface area shrinkage is deduced from the bulk shrinkage as:
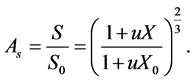 (4)
(4)
u is determined from experimental shrinkage data. Assuming an ideal shrinkage during diffusion period, the value of u is evaluated from a linear fitting of volume ratio versus dimensionless moisture content according to the following formula [2] :
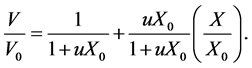 (5)
(5)
3.2. Thin Layer Drying Model
3.2.1. Hypothesis
To model the thin layer drying of mango slices, it was assumed that:
- The transfers are unidirectional.
- The dryer is cut off along its length (in the air flow direction) in sections of Dx thick.
- The temperature and moisture content in each section are invariable.
- Physical parameters vary “step by step” in each tray and from one tray to another.
- Exchanges into each tray are determined by the exit conditions of drying air from the preceding tray.
- The drying rates are known by experiment carried out in laboratory.
- The humid air and its components (water vapour and dry air) are ideal gases at the drying pressures.
- The air flow is constant and the thermal losses at the dryer bottom are neglected.
Taking the assumptions above into account, the depending variables of the model are:
- T5 drying air temperature (K, ˚C).
- T4 slices temperature (K, ˚C).
- T3wi internal wall temperature (K, ˚C).
- T3we external wall temperature (K, ˚C).
- Cv mass fraction of the water vapour in the air.
- Ci mass fraction of the water vapour in the product.
These variables evolve according to the fixed variables which are:
- t time (s).
- x x-coordinate in the direction of the air flow across the drying bed (m).
3.2.2. Transfer Equations
The energy balance on each section of the dryer was written as:
- Heat balance on the dryer walls
Þ Internal wall:
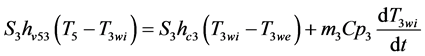 (6)
(6)
Þ External wall:
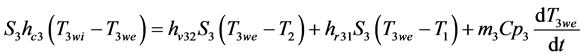 (7)
(7)
- Energy balance on the air
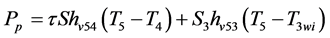 (8)
(8)
 (9)
(9)
- Heat balance on the product
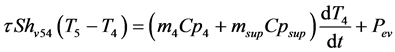 (10)
(10)
With:
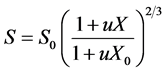 (11)
(11)
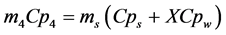 (12)
(12)
- Heat balance on the air and the product
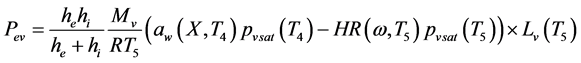 (13)
(13)

With:


where: S is the current surface of exchange of slices, S0 the surface of air-tray contact, the contact rate of tray- product, 
3.3. Simulation of Transfers
The drying simulation was carried out by using the average data on the drying characteristics of “Kent” mango variety and the thermophysical properties of the drying air showed in Table 2. The water content of mango slices in thin layer was supposed to be uniform. It was obtained from the transfer equations, a simultaneous equations system solved by iterations through an explicit method using a simulation program adapted to software MATLAB version 7.0.1.
4. Results and Discussions
4.1. Shrinkage and Isotherm Curves
4.1.1. Shrinkage
Volume ratios versus dimensionless water content of Kent mango samples for 40˚C, 50˚C, 60˚C and 70˚C are were presented on Figure 2. These shrinkage curves have almost linear profiles at each level of drying. Each
Table 2. Drying characteristics of mango and thermophysical properties of drying air used in model.
Figure 2. Shrinkage curves of Kent mango at 40˚C - 70˚C.
curve showed an almost linear profile with a slope very close to unity at the beginning of drying and slightly higher than unity towards the last stages of drying. It can be deduced that for Kent mango as well as for other variety of mango, the shrinkage is almost ideal and the volume of lost water during the process is then almost equal to the drying product volume reduction. The volume reduction is slightly higher than evaporated water volume only for the latest drying stages. That is due to a simultaneous volume reduction of gas and solid matter of drying product as noticed by May & Perré [11] for apple. This ideal shrinkage behaviour of Kent mango samples proves that the dry Kent mango should be a compact product with a low porosity, as reported by Dissa et al. [2] . The linear fitting of experimental shrinkage data allowed establishing a correlation used for drying kinetic correction for shrinkage. The value of the linear shrinkage coefficient deduced from this expression is u = 1.472.

4.1.2. Desorption Isotherm
The variation of equilibrium moisture content (Xeq) as a function of the water activity of Kent mango at 40˚C is presented in Figure 3. The desorption curves at 40˚C present almost constant equilibrium moisture contents for low water activities (Aw < 0.3). According to Van den Berg & Bruin (1981), most of biological products are preserved for activities lower than 0.6, because microorganisms can no longer take up the water necessary for their development and enzymes become inactive. This 0.6 activity of preservation for biological product was confirmed by Pott, Neidhart, Mühlbauer, & Carle [12] for non-sulphited dried mangoes. According to Figure 2 the equilibrium moisture content corresponding to that limit of micro-organisms development (aw < 0.6) is 58.27% (db) at 40˚C for Kent mango. A modified Henderson model was used to obtain the desorption curve for many temperatures. The fitting of experimental data with this model lead to the following correlation of the desorption isotherm:

4.2. Drying Kinetics
The experimental and modelled convective drying kinetics (X/X0 vs. time) obtained for 5 mm thickness mango slices at 50˚C, 60˚C and 70˚C are presented on Figure 4. The initial water content used was 6.01 d.b. One can
Figure 3. Experimental and simulated desorption isotherm of Kent mango at 40˚C.
Figure 4. Experimental and simulated convective drying kinetics of 5 mm thickness Kent mango slices at 50˚C, 60˚C and 70˚C (Vair = 0.8 m/s, RHair = 15%).
easily notice that the product reached its equilibrium moisture content in 80 min at 70˚C, 150 min at 60˚C and 210 min at 50˚C. According to Figure 4, experimental and simulation results were very close. The correlation coefficient of fitting experimental data by simulation curves was r2 = 0.997. Therefore, it can be deduced that experimental drying kinetics of Kent mango can be approached by the model. Thus, the thin layer drying model may be assumed to represent suitably Kent mango slices convective drying kinetics profile. The final water content obtain was about 0.23 X0 i.e. 13.8% d.b. This final water content of mango slices was in the range 12% - 20% w.b. of previous work reported by Touré and Kibangu-Nkembo [6] and very close to 13% w.b. that obtained by Gbaha et al. [4] .
5. Conclusion
A model of convective thin layer drying of mango slices was developed and validated by experiments in this study. The drying kinetics and the temperature curves of the product were simulated using the model at various drying temperatures. The simulated curves were then compared to the experimental curves obtained using a convective dryer controlled in temperature and moisture. Our results showed that the drying curves were suitably fitted by the thin layer drying model with a correlation coefficient r2 = 0.997. Thus, taking shrinkage into account, it is possible to predict more effectively the thin layer drying kinetics of Kent mango slices.
Cite this paper
Alfa OumarDissa,JeanKoulidiati,HélèneDesmorieux, (2016) A Convective Thin Layer Drying Model with Shrinkage for Kent Mango Slices. Advances in Chemical Engineering and Science,06,20-28. doi: 10.4236/aces.2016.61002
References
- 1. Dissa, A.O. (2007) Séchage convectif de la mangue: Etude de l’influence des paramètres aérauliques et intrinsèques, conception et modélisation du fonctionnement d’un séchoir solaire indirect. Thèse de Doctorat Unique, Université de Ouagadougou, Burkina Faso.
- 2. Dissa, A.O., Desmorieux, H., Bathiebo, J. and Koulidiati, J. (2008) Convective Drying Characteristics of Amelie Mango (Mangifera indica L. cv. “Amelie”) with Correction for Shrinkage. Journal of Food Engineering, 88, 429-437.
http://dx.doi.org/10.1016/j.jfoodeng.2008.03.008 - 3. Dissa, A.O., Bathiebo, J., Kam, S., Savadogo, P., Desmorieux, H. and Koulidiati, J. (2009) Modelling and Experimental Validation of Thin Layer Indirect Solar Drying of Mango Slices. Renewable Energy, 34, 1000-1008.
http://dx.doi.org/10.1016/j.renene.2008.08.006 - 4. Gbaha, P., Yobouet Andoh, H., Kouassi Saraka, J., Kaménan Koua, B. and Touré, S. (2007) Experimental Investigation of a Solar Dryer with Natural Convective Heat Flow. Renewable Energy, 32, 1829-1817.
http://dx.doi.org/10.1016/j.renene.2006.10.011 - 5. Madhlopa, A., Jones, S.A. and Kalenga, S.J.D. (2002) A Solar Air Heater with Composite-Absorber Systems for Food Dehydration. Renew Energy, 27, 37-27.
http://dx.doi.org/10.1016/S0960-1481(01)00174-4 - 6. Touré, S. and Kibangu-Nkembo, S. (2004) Comparative Study of Natural Solar Drying of Cassava, Banana and Mango. Renewable Energy, 29, 990-975.
http://dx.doi.org/10.1016/j.renene.2003.09.013 - 7. AOAC (1990) Official Methods of Analysis. No. 934-06. Association of Official Chemists, Washington DC.
- 8. Myara, M.R. and Sablani, S. (2001) Unification of Fruit Water Sorption Isotherms Using Artificial Neural Networks. Drying Technology, 19, 1543-1554.
http://dx.doi.org/10.1081/DRT-100107258 - 9. Michel, D. (1985) Séchoirs Solaires: Théorie et Pratique. UNESCO, France, 568224.
- 10. Desmorieux, H. (1992) Le Séchage en Zone Subsaharienne: Une analyse Technique à Partir des Réalités Géographiques et Humaines. Thèse Présentée à l’INPL, Loraine, France.
- 11. May, B.K. and Perré, P. (2002) The Importance of Considering Exchange Surface Area Reduction to Exhibit a Constant Drying Flux Period in Foodstuffs. Journal of Food Engineering, 54, 271-282.
http://dx.doi.org/10.1016/S0260-8774(01)00213-8 - 12. Pott, I., Neidhart, S., Mühlbauer, W. and Carle, R. (2005) Quality Improvement of Non-Sulphited Mango Slices by Drying at High Temperatures. Innovative Food Science and Emerging Technologies, 6, 412-419
http://dx.doi.org/10.1016/j.ifset.2005.05.004
NOTES
*Corresponding author.








