Received 28 April 2016; accepted 27 June 2016; published 30 June 2016

ABSTRACT

Modeling highway traffic crash frequency is an important approach for identifying high crash risk areas that can help transportation agencies allocate limited resources more efficiently, and find preventive measures. This paper applies a Poisson regression model, Negative Binomial regression model and then proposes an Artificial Neural Network model to analyze the 2008-2012 crash data for the Interstate I-90 in the State of Minnesota in the US. By comparing the prediction performance between these three models, this study demonstrates that the Neural Network is an effective alternative method for predicting highway crash frequency.

Keywords:

Poisson Regression, Negative Binomial Regression, Artificial Neural Network, Crash Frequency

1. Introduction

Highway safety is a global concern, and a socio-economic aspect, leading to tremendous life and property loss each year around the world, and therefore a comprehensive understanding of the traffic safety system is always emphasized in transportation engineering. Public agencies have put great effort into preventive measures, such as illumination and policy enforcement; however, the annual number of traffic accidents has not yet significantly decreased. For instance, in the US according to the 2012 crash overview report, published in Feb 2014 by the fatality analysis reporting system (FARS) and the national automotive sampling system-general estimates system (NASS-GES), a total of 33,561 people were killed in motor vehicle crashes in 2012 with 3.3% increase over 2011 fatalities, and an additional of 2,362,000 people were injured in crashes with an increase of 6.5% over 2011 injuries. Therefore, there should be further research studies on the risk factors associated with traffic accidents. The occurrence of crashes can be attributed to driver, vehicle, environment, and roadway characteristics. This paper begins with a literature review of modeling accident frequencies, followed by a description of the data used in the analysis, then introduces the methodological approach of evaluating Poisson regression and Negative Binomial regression, and then proposes the Artificial Neural Network approach to improve upon the two previous methods, followed by discussion of findings, and comparison of results. The paper concludes with a summary and directions for future researches.

2. Literature Review

Modeling of crash count data is very important topic in highway safety analysis, and in the past few decades, modelers have proposed a significant number of analysis tools for analyzing crash data. The number of crashes per year (or per more than one year, such as five years) is called the crash frequency, which has been widely used as an indicator of the crash occurrence at highways or certain segments of the roads. A variety of independent variables can affect crash frequency that are related to the driver behaviors, road geometric, vehicle, and environment. The influence of such variables on crash occurrence could significantly vary on case by case basis, but in general, past researches have shown that both behavioral factors related to the driver’s errors, and non- behavioral factors related to the road geometry, vehicle, and environment can significantly affect traffic accidents, and researchers usually extract only a limited number of variables from each class to be used as independent variables in the modeling process [1] . Previous researches in the literature that attempted to estimate crash frequency can be classified into two types. One type includes conventional univariate regression models, such as the Poisson regression model, Poisson-Gamma (Negative Binomial) model, Poisson-lognormal model, zero-inflated model, and Conway-Maxwell-Poisson model. The second type includes more specification-based models such as generalized additive models, random-parameters models, finite mixture, Markov switching models, and hierarchical models [2] . Crash prediction models were first based on the simple Multiple Linear Regression models assuming normally distributed errors. However, researchers soon discovered that crash occurrence is more fitted with the Poisson distribution, and hence began to utilize the Poisson regression model that was developed by an advanced modeling technique called the Generalized Linear Models (GLM), instead of the conventional multiple linear regression technique [3] . The Multivariate Poisson (MVP) regression models have been used for several decades, and become one of the most popular modeling techniques in the traffic safety field, especially for crash rate or crash frequency estimation. Several papers in the literature, such as [4] - [6] produced an MVP model approach to explore the relationship between the risk factors and crash rates. However, many researchers have found that the Poisson regression model has one important constraint that is the mean must be equal to the variance, and when this assumption is violated, the standard errors estimated by the maximum likelihood method, will be biased and the test statistics derived from the model will be incorrect. Since recent studies have shown that the accident data were usually over-dispersed (i.e. the variance is much greater than the mean), therefore, this will result in incorrect estimation of the likelihood of accident occurrence when using the Poisson regression model [2] . In overcoming the problem of over-dispersion, researchers began to employ the Negative Binomial (NB) distribution (or Poisson-Gamma) instead of the Poisson distribution, which relaxes the condition of mean equals to variance, and hence can take into account the over-dispersion in the crash data counts [2] . The NB models have been widely used in crash frequency modeling, and several papers can be found in the literature addressing the NB models, such as [7] - [12] . However, the NB model has some limitations such as its inability to handle the case of under-dispersion of the data count, where the mean of the crash counts is higher than the variance, and this (although rare) can exist when the sample size used is very small, and the mean value is too low, which can result in inadequate parameter estimates [13] [14] . Hence, to overcome the limitations of the NB models, some researchers introduced the Poisson-Lognormal model, in which the error term is Poisson-lognormal rather than gamma-distributed, and can handle the under-dispersed data counts [11] [12] [15] [16] . Another widely used crash frequency modeling that can be found in the literature is the zero-inflated Poisson and zero-inflated negative binomial models, which have been introduced mainly to deal with the over-dispersion problem caused by the excessive zeroes (i.e. locations where no accidents can be observed) in traffic accident data counts. The zero-altered procedure allows modeling the accident frequencies in two states, namely; the zero-accident state, and the non-zero accident state (where accident frequencies follow some distribution occurrence, such as the Poisson or negative binomial distribution), and the probability of a section being in zero or non-zero states can be found by a binary log it model or a probit model. These zero-inflated models have shown great flexibility in both states, although some researchers have criticized their applications in crash predictions because of the long term mean equals to zero in the safe state, and hence, it can produce some biased estimates [10] [17] . The Conway-Maxwell-Poisson model has been recently investigated in highway safety researches, but it has limited applications in crash frequency modeling [9] [18] . A limited number of researches have used the Generalized Additive Models that can provide smoothing functions for the explanatory variables, however their estimation process can become very difficult to be employed as they include more parameters than the traditional count models, and therefore their applications to the crash frequency prediction are very limited [19] [20] . Random-parameters models have also been used in few researches to take the effect of the unobserved heterogeneity from one roadway site to another, but they have been very limited in their applications [21] - [23] . Finite mixture and Markov switching models have been used recently in some limited applications of highway safety and crash frequency, but still they are very complex in their processing procedures to be widely employed [10] [24] [25] . Hierarchical-multilevel models have also been used in crash frequency modeling to address the effect of large correlation within the hierarchical clustering if exist, but their outputs are very difficult to be interpreted, and have not been popular in their applications [8] . Artificial Neural Networks (ANNs) have been employed in some applications of highway safety as predictive tools, such as driver behavior analysis, pavement maintenance, vehicle detections, traffic signal control, and vehicle emissions [26] - [28] . However, their applications in crash frequency analysis have been extremely few, and therefore this paper examines whether ANNs can be used as an alternative method to determine the relationships between the risk factors and crash occurrence by comparing their performance with other methods.

3. Data Source and Description

Data were obtained from the Highway Safety Information System (HSIS) database maintained by the Federal Highway Administration (FHWA) of the United States Department of Transportation. This paper used a 5-year crash period extending from 2008 to 2012 on the interstate highway (I-90) in the state of Minnesota. The interstate I-90 is a multi-lane divided highway that connects the eastern and western coasts of the US, and it passes through the southern part of Minnesota with a length of 444 km (276 mi). The data provided by the HSIS for Minnesota was carefully examined, labelled, filtered, and outliers and missing data were excluded from the analysis. All crashes that occurred on the I-90 during the study period 2008-2012 were considered in the analysis including fatal, different levels of severity injury, and property damage crashes. The data from the HSIS were obtained in three separate folders: the accident files, the road files, and the vehicle files on a year-by-year basis for the state of Minnesota. The accident files contained information about the crashes, the environment, and the circumstances of the crash occurrence. The vehicle files described various characteristics of the vehicle(s) involved. The road files provided information on the road characteristics where the accidents occurred. For the purposes of this study, the three data files for each of the 5 years period were combined to create a single dataset of the crash records containing all relevant data about the drivers, roads, environment, and vehicles involved in these crashes. The (I-90) study area was divided into manageable and homogenous roadway sections, such that within each section there was reasonable constancy of geometric characteristics so that each section can be treated as an observation in the dataset. The total length of I-90 in MN (444 km) was disaggregated into 897 sections with section length varies from 0.2 km to 0.9 km. Different risk factors related to the road geometry, the driver behavior, the environment, and the vehicles involved in the crashes were carefully examined, classified, and pertaining with previous studies in the literature, the following group factors were chosen to be included in the analysis: the road characteristics factors (i.e. straight segments, upgrades, downgrades, horizontal curves);the road surface conditions (i.e. dry, wet, muddy); the section lengths; the weather conditions (i.e. clear, rain, snow, fog); the annual average daily traffic (AADT) of each section; the light conditions (i.e. day light, dark with street light on, dark and no light);the driver age; the driver sex; and the vehicle type (i.e. passenger car, van, bus, truck).The number of lanes, width of lanes, shoulder widths, and route classifications have been widely used in the literature as contributing factors in the analysis of crash prediction, however they were removed from this study because the interstate I-90 mostly consists of homogenous and fixed number of lanes and shoulders throughout the study area, and therefore they cannot contribute to the crash frequency in this paper. The HSIS criteria for labelling and classifying of the risk factors were used in the analysis. The data were randomly divided into two subsets, one for the training process that includes 70% of the observations, and the other for testing process that includes 30% of the observations. Hence, the total number of the road sections (897) was disaggregated into 628 sections for the training data, and 269 sections for the testing data. Table 1 shows the risk factors (i.e. the explanatory variables) included in the analysis, their name interpretations, and their statistics.

The correlation between all the explanatory (independent) variables were tested using Pearson correlation test in order to exclude the highly correlated variables (i.e., correlation of 60% or more), and the correlations were

found to be very low among all variables (i.e. no correlation value exceeded 21%), and therefore all the selected explanatory variables were kept in the analysis. The observed crash frequency of I-90 at all road sections from 2008 to 2012 ranges from 0 to 7, the average frequency is 0.77, sections with zero crash frequency are 480, and sections with only one crash frequency are 286, as shown in Figure 1.

4. Methodology

Two widely used crash prediction approaches were chosen for the analysis of crash data of the interstate highway I-90 in Minnesota; namely the Poisson Regression Model, and the Negative Binomial (NB) Regression Model. In order to improve the prediction outputs, a new approach was proposed for conducting the analysis, and comparing the results namely; the Artificial Neural Network (ANN) model as described below:

1―The Poisson Regression Model

Poisson regression model was widely used in the past few decades as an introductory method of modeling the highway crash prediction because it can easily handle the nature of the crash frequency data counts, which are often described as random events, discrete, and non-negative integers, and often their distributions were found to be skewed, and close to the Poisson distribution rather than other distributions such as the normal distribution [2] [6] [29] . The Poisson model can be expressed as:

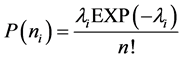(1)

where,

P(n_i): the probability of n crashes occurring on section i of a highway during a period of time,

λ_i: the expected crash frequency on section i of the highway.

Accordingly, the crash frequency can be estimated by the expression:

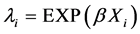(2)

where,

λ_i: the dependent variable (the expected number of crashes per time period),

X_i : a vector of the independent (explanatory) variables,

β: a vector of the estimates (coefficients) of the independent variables X_i.

The Poisson model assumes that the mean equals the variance, and hence can’t handle the over-dispersion nature of the crash data when the variance exceeds the mean, especially if the sample size is small [2] [14] . A crash frequency analysis was conducted on both the training and testing datasets using the Poisson regression model, and the results of the Poisson model fit were obtained by using the SPSS software as shown in Table 2. Since the Poisson regression model is a form of the Generalized Linear Models (GLMs), therefore many goodness of fit measures can be used for estimating how well the model fits the data, such as the deviance, and Pearson Chi square. If the model fits the data well, the ratio of the deviance to the degrees of freedom (df), and the ration of the Pearson Chi square to the degrees of freedom should be close to one [7] - [10] . Table 2 shows that both the deviance/df (unitless), and the Pearson Chi square/df (unitless) for both the training and testing data are significantly larger than one, indicating that the Poisson regression model might not be well suited for these data, apparently because of the over dispersion in the data count, that cannot be handled effectively by the Poisson regression. The overall model fit determined by the software is 53.45% for the training data, and 55.87% for the testing data, as shown in Table 2.

2―The Negative Binomial (Poisson-Gamma) Regression Model (NB)

The Negative Binomial (or Poisson-Gamma) Regression Model is the most commonly used model in crash frequency modeling, and it was introduced as an alternative to the Poisson Regression Model to take into account a possible over-dispersion in the crash data counts. The NB uses Gamma Probability Distribution, and can relax the assumption of the mean equals the variance that the Poisson regression model takes into account, and hence the NB can deal with the over-dispersion that usually exists in the crash data counts. In order to obtain the NB model, the Poisson regression can be rewritten by adding an error term to its predicted number of crashes, and becomes:

(3)

where:

: a gamma-distributed error with mean equals one and variance equals α.

This error term which is called the over-dispersion parameter, allows the variance to differ from the mean

such that:

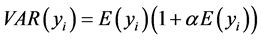(4)

where,

VAR(y_i): the variance of the dependent variable y_i,

E(y_i): the expected mean value of the dependent variable y_i.

and both α and β can be estimated from the maximum likelihood function. When α is zero, the model becomes Poisson regression, and if α is found to be significantly different from zero, then the NB regression can be used instead of the Poisson regression model [2] [9] [26] . A crash frequency analysis was conducted on both the training and testing datasets using the Negative Binomial regression model, and the results of the NB model fit were obtained by using the SPSS software as shown in Table 3. The NB model also belongs to the GLMs, and as was the case in Poisson regression, if the model fits the data well, the ratio of the deviance to the degrees of freedom, and the ration of the Pearson Chi square to the degrees of freedom should be close to one. Table 3 shows that both the deviance/df (unitless), and the Pearson Chi square/df (unitless) for both the training and testing data are very close to one, indicating a good fit of this model. The overall model fit is 59.18% for the training data, and 61.88% for the testing data, indicating much better fits than the results obtained from the Poisson regression, apparently because the NB can easily handle the over dispersion nature of the data counts, and hence can effectively improve the overall fit and prediction results.

3―The Artificial Neural Network (ANN)

Artificial Neural Networks (ANNs) are robust functions and analytical tools for prediction and classification problems that can model very complex non-linear functions to high accuracy levels using a process of learning that is similar to the learning procedure of the cognitive system in the human brain. The network body is composed of a series of nodes and weight factors that connect the nodes together in hierarchical style that consists of input layers, hidden layers, and output layers. These models have been used in recent years in many research areas including highway safety as predicting approaches, and researches have shown that they can predict complex observations more accurately than the traditional regression models. ANNs have many advantages over the classical statistical models. For instance, regression models need a pre-defined relationship or functional form between the dependent variable (crash frequency) and the independent explanatory variables that can be estimated by some statistical approaches, whereas the ANNs do not require the establishment of these functional forms, and can be easily applied for the analysis. On the other hand the ANNs differ from the statistical models in that they behave as black-boxes and do not provide interpretation for the parameter estimates related to the explanatory variables [2] [27] [28] . In this paper, a three-layer Neural Network has been used consisted of an input layer with 9 explanatory variables that contained a total of 27 subunits, the hidden layer with 8 neurons, and the output layer that represents the 8 classes of the crash frequency occurrence on the I-90 in MN (i.e. sections with 0, 1, 2, 3, 4, 5, 6, 7 crash rate occurrence), and the structure of the Neural Network is shown in Figure 2. The same independent variables that were introduced into the Poisson regression and the Negative Binomial regression models were fed into the input layer of the ANN for the purpose of the performance comparison between the different models. The number of the neurons in the hidden layer were tested for optimization using the cross-validation design experiment by the SPSS software, and the optimal number was found to be 8 (i.e. 7 neurons plus the bias neuron). The output layer was set to predict the crash frequency at each section of the I-90. The data were randomly divided into two subsets as was already done for the Poisson and the NB models, the training data which consists of 70%, and the testing data consists of 30% of the total observations. The back propagation algorithm was employed for training the Neural Network in this study, as it is currently the most widely used rule for training neural networks, which tries to minimize the total mean square error (MSE) of the output as follows [26] :

(5)

where,

MSE: the mean square error,

t: the target output,

α :the model output,

K: the number of neurons,

N: the number of observations in the data.

The software default hyperbolic tangent activation function was used for processing the hidden layer, and the soft max activation function was used for the output layer. The best MSE results for the training and testing data were obtained after conducting thousands of learning cycles by the Tiberius software. The results of the overall model fit, and the overall model error determined by the software for both the training and testing data are shown in Table 4. The overall ANN fit is 69.3% for the training data, and 70.2% for the testing data, and the overall error for the training data is 6.3% and for the testing data is 5.7%. These results show that the ANN can fit the training and testing datasets much better than the Poisson and the NB models, and thus, a significant improvement has been achieved by using the ANN model over the Poisson and the NB model fits.

5. Discussion of Findings

The results of the coefficient’s estimates of the explanatory variables for the testing data from both the Poisson regression, and the NB regression models are shown in Table 5. The Wald Chi square statistics shown in the table is a popular way of testing the significance (similar to the t-statistics) of the explanatory variables used in the Generalized Linear Models, such as Poisson and NB models. If the Wald statistics turned to be significant for any variable (as indicated by the associated p-value), then this variable is significant, and should be kept in the model, and if not, then this variable can be omitted from the model [9] - [12] . Since the Wald statistics shown in

the table are significant at the 95% confidence level for all the explanatory variables used in the model (i.e., their p-values are less than 0.05) except for the clear weather condition (with p-value of 0.077 in the Poisson model, and 0.079 in the NB model), and the day light condition (with p-value of 0.092 in the Poisson model, and 0.107 in the NB model), then these two factors can be omitted from the model, and all other factors are significant, and should be kept. Also, the coefficient’s estimates and their signs for the testing data in both Poisson and NB models shown in Table 6 can be used to explore the contribution of each explanatory variable to the resulting dependent variable (i.e. crash frequency). The positive sign of the estimate indicates that the associated explanatory variable would increase the likelihood of the crash occurrence, and the negative sign indicates negative contribution of the variable to the crash occurrence. For example, when inspecting the road characteristics factors in both the Poisson and NB models, the positive sign of the upgrade, downgrade, and horizontal curves means that the occurrence of crashes at road segments with these features are more likely to happen than at the straight portions of the road. The grades and curves affect the operation of vehicles and their speed, and this obviously could increase the probability of the vehicle accidents. The wet, and muddy conditions of the road surface would decrease the coefficient of friction between the tires and the road surface, and hence would increase the crash probabilities, as indicated by the positive sign of the wet and muddy coefficient estimates compared to the negative sign of the dry condition estimate. For the weather factors estimates, the positive sign of the snow, and fog conditions indicates increased crash frequency at these conditions, as the driver vision within the fog could decrease, and the friction coefficient within the snow could substantially decrease, and hence, causing the increased probability of more accidents. The accidents could also increase in the dark with no light, as indicated by the positive sign of the (No light) factor estimate in the table. The driver age group of (21 to 65 years) has negative estimate, indicating that this group is less likely to increase the crash occurrence, whereas the young drivers (less than 21 years), and the elderly (more than 65 years) can positively contribute to the increased crash frequency, as indicated by their positive sign estimates. The driver sex has negative estimates for both males and females, indicating no preferences on crash occurrence in term of driver sex. The vehicle type factors show that both the passenger cars and vans or mini vans have negative sign estimates, meaning that their contribution to the accidents is less likely to increase, compared to the buses and trucks with positive estimates that can increase the crash occurrence likelihood. The negative sign of the section length estimates shows that the different section lengths have no effect on the increased accident probability. The annual average daily traffic (AADT) has positive estimate sign, indicating that the increased daily traffic volume at any section can increase the crash frequency as vehicles are more likely to interact with each other in higher volume conditions.

The ANN model can directly determine the % importance of each explanatory variable in predicting the output (crash frequency) as shown in Table 6. The road characteristics factors (road geometry) have the highest importance of 42% in determining the crash occurrence rate as shown in the table, and this is obvious because the road geometrics can affect the operational speed of the vehicles, especially on the grades and curves, and hence, increasing the likelihood of the crash occurrence. The second important explanatory variable is the AADT with 27.9%, indicating that the increased traffic volume at any section of the road can increase the prob-

ability of the crash occurrence resulting from the increased interaction between vehicles. The importance of the weather factors is 6.7%, indicating that the adverse weather conditions, such as snow and fog conditions, could increase the probability of the crash occurrence by 6.7%. Next, the importance of the driver age is 5.2%, indicating that the driver age can contribute to the crash occurrence, especially for young drivers (less than 21 years), and elderly drivers (more than 65 years) by as much as 5.2%. Next, the vehicle type (i.e., passenger car, van, bus, truck) with 5.1% importance. Next, the road surface factors with an importance of 4.3%, indicating that these factors (i.e., dry, wet, muddy) can contribute to the crash occurrence by 4.3%. The light conditions factors have 4.2% importance on the crash frequency, and the section length has only 2.6% importance. The least important variable is the driver sex with only 2% contribution to the crash occurrence.

This classification tool from the ANN model is very useful in determining the most influential explanatory variables that can contribute to the crash occurrence instead of using the coefficient estimates from the Poisson and NB models. This % importance is easier to be interpreted than the estimates and their signs in the other two regression models. Furthermore, the ANN does not require pre-defined relationships between the independent and the dependent variables, and can be easily applied in the crash frequency analysis.

6. Comparison of Prediction Performance between the Three Approaches

The prediction performance of the three models used in this paper can be presented by comparing the observed crashes versus the predicted crashes for each model at each crash occurrence rate, as shown in Table 7 for both the training and testing data. The ANN crash prediction results are much better than the NB, and Poisson models in all crash occurrence rate (i.e. within sections of 0, 2, 3, 4, 5, 6, 7), except for sections with one crash occurrence rate for the training data, where the NB performs better, followed by the Poisson model. Also, the overall prediction performance of the ANN is much better than the NB, and Poisson models for the testing data. The overall prediction performance of the ANN is 74.4% compared to the NB overall performance of 63.7% and the Poisson performance of 54.9% regarding the testing data. These prediction results of the ANN demonstrate that the ANN model is an effective approach in predicting highway crash frequency, and can improve the accuracy of the prediction results upon the results obtained from the traditional statistical models, such as the NB, and the Poisson regression models.

7. Conclusion

In this paper two crash prediction methods were analyzed using the crash data counts on the interstate highway I-90 in Minnesota, namely; the Poisson Regression Model, and the Negative Binomial (NB) Regression Model. Then the Artificial Neural Network (ANN) approach was used as a third method. The analysis showed that the Poisson model might not be well suited to fit the crash data counts because it assumes that the mean must equal the variance, and hence, it cannot deal with the over-dispersion nature of the crash data counts. The NB can take

the over-dispersion into account, and hence, can produce better prediction results. However, the prediction results obtained from the ANN model were superior to the other two methods, and hence, this paper recommends employing the ANNs in crash frequency modeling, as they can predict results with much more accuracy than the traditional statistical models, and can directly determine the importance of each explanatory variable without the need of statistical estimates to interpret the results. In addition, the ANNs do not require pre-defined relationships between the risk factors, and the crash frequency compared to the traditional statistical models. Also, when applying the ANN in the analysis of crash frequency, the correlation problems between the explanatory variables would not be a concern, because ANN can effectively handle the correlation problem without affecting the output. Future work might focus on how to improve the prediction performance of the ANN models in crash modeling by using different training algorithms than the back propagation algorithm, different number of neurons in the hidden layer that could further improve the results of prediction, and different activation functions for processing the hidden and output layers.

Acknowledgements

The author would like to thank the Highway Safety Information System (HSIS) for providing the MN crash data for the years (2008-2012) that were used in the analysis.

Cite this paper

Azad Abdulhafedh, (2016) Crash Frequency Analysis. Journal of Transportation Technologies,06,169-180. doi: 10.4236/jtts.2016.64017

References