Journal of Transportation Technologies
Vol.4 No.1(2014), Article ID:41973,11 pages DOI:10.4236/jtts.2014.41002
Real-Time Short-Term Forecasting Based on Information Management
1Faculty of Exact Science, Computer Science Department, Al Qasemi Acedemic College, Haifa, Israel
2Faculty of Civil and Environmental Engineering, Department of Transportation Engineering, Technion-Israel Institute of Technology, Haifa, Israel
Email: raiyn@qsm.ac.il, toledo@technion.ac.il
Received August 11, 2013; revised September 12; 2013; accepted October 9, 2013
ABSTRACT
Traffic congestions and road accidents continue to increase in industry countries. There are three basic strategies to relieve congestion. The first strategy is to increase the transportation infrastructure. However, this strategy is very expensive and can only be accomplished in the long-term. The second strategy is to limit the traffic demand or make traveling more expensive that will be strongly opposed by travelers. The third strategy is to focus on efficient and intelligent utilization of the existing transportation infrastructures. This strategy is gaining more and more attention because it’s well. Currently, the Intelligent Transportation System (ITS) is the most promising approach to implementing the third strategy. Various forecast schemes have been proposed to manage the traffic data. Many studies showed that the moving average schemes offered meaningful results compared to different forecast schemes. This paper considered the moving average schemes, namely, simple moving average, weighted moving average, and exponential moving average. Furthermore, the performance analysis of the shortterm forecast schemes will be discussed. Moreover, the real-time forecast model will consider the abnormal condition detection.
Keywords:Forecast Scheme; Moving Average; Intelligent Transportation System
1. Introduction
This paper introduces a modern forecast strategy. Conceptually, traffic information [1,2] may fall into one of the three categories as follows: historical information, real-time information, and predictive information. The historical data [3,4] are a collection of past observations of the system. Real-time information is the most up-todate and can be calculated, e.g., by on-line simulations. The real-time information achieves to update the historical adaptive information, special in the case that the realtime information does not match the historical information. To optimize the forecast algorithm, we have collected travel data by the mobile phone. For a successful forecast of traffic flow, it ought to apperceive the variety of environment and can adjust the parameters automatically. Furthermore, it is important that the forecast model takes into consideration the abnormal conditions that occurred in real-time [5,6]. The paper is organized as follows. Section 2 describes the problem in transportation engineering. Section 3 introduces the information collection based on cellular phone services. Section 4 introduces the short-term forecast scheme based on historical and real-time information. Section 5 discusses the performance analysis of the proposed short-term forecast scheme based on exponential moving average.
2. Methodology
The purpose of this paper is to assess the strengths and limitations of available of the traffic data collection based on the cellular mobile services and their corresponding processing algorithms. The performance of an incident detection system is determined on two levels:
data collection technologies and data processing algorithms. Variations in cellular mobile services [7] and algorithm schemes result in a variety of solutions for incident detection. Various short-term traffic forecasting scheme have been proposed [8-19]. In this section we introduce the forecast model based on the moving average. There are three types of moving average, that is, simple moving average (SMA), weight moving average (WMA), and exponential moving average (EMA) [20- 23]. In this study, an exponential moving average is considered. An exponential moving average uses a weighting or a smoothing factor which decreases exponentially. The weighting for each older data point decreases exponentially, giving much more importance to recent observations while not discarding the older observations entirely. Figure 1 illustrated the proposed forecast model. The forecast model is divided into two phases, namely, detection phase, and forecast phase. The detection phase focused on the collected data analysis. To increase the accuracy of the forecast model we need to detect the abnormal events in the collected data. The forecast scheme is based on the exponential moving average. The robustness and accuracy of the exponential smoothing forecast is high and impressive. The accuracy of the exponential smoothing technique depends on the weight smoothed factor alpha value of the current demand. To determine the optimal alpha factor value we use the fitting curve.
There are two kinds of exponential moving average forecasting (EMA) that is exponential moving average based historical information (EMA-H) and exponential moving average based real-time information (EMA-R). The EMA-R consists of two main phases, namely detec-
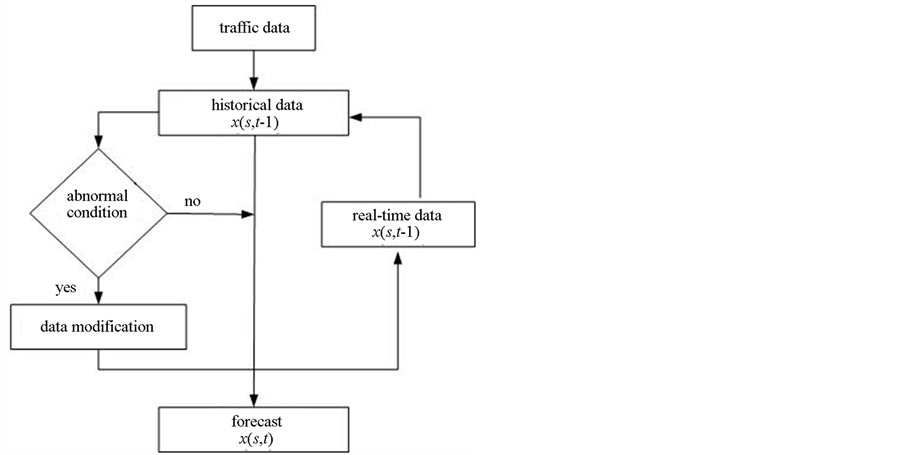
Figure 1. Algorithm process.
tion phase and forecast phase
2.1. Forecast Based Historic Observations
The historical database is a collection of past travel observations of the system. Exponential smoothing is forecasting method that gives weight to the observed time series unequally. The unequal weight is accomplished by using one or more smoothing parameters, which determine how much weight is given to each observation. The major advantage of exponential smoothing methods is that gives good forecasts in a wide variety of applications. In addition, data storage and computing requirements are minimal, which makes exponential smoothing suitable for real-time application.
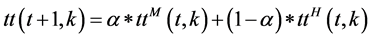 (1)
(1)
where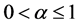 ,
, 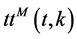 the actual travel time in section
the actual travel time in section 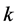 at the time
at the time 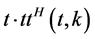 the historical travel time in section
the historical travel time in section 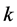 at time
at time .
.
Smoothed Parameter Alpha
To achieve short-term traffic flow forecasting with high accuracy, the proposed forecast scheme required to optimize the smoothed parameter alpha. Alpha determines how responsive a forecast is to sudden jumps and drops. It is the percentage weight given to the prior, and the remainder is distributed to the other historical periods. Alpha is used in all exponential smoothing methods. The lower the value of alpha, the less responsive the forecast is to sudden change. The smoothing parameter “alpha” lies between 0 and 1. To determine the optimized smoothing factor, a sum of the square errors between the observed and the forecasted alpha dose rates was analyzed by increasing the smoothing filter factor from 0.1. Sum of the square errors is decreased as the smoothing filter factor is increased as showed in Figure 2.
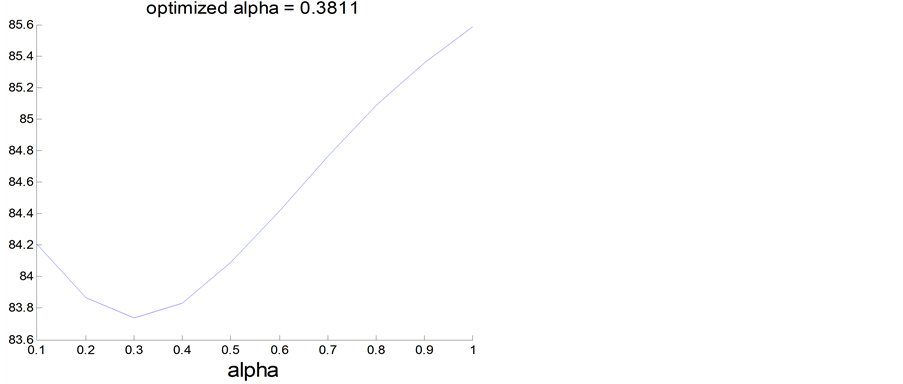
Figure 2. Smoothed parameter alpha.
2.2. Real-Time Forecasting
Occurrence of Abnormal conditions in flow travel information decrease the accuracy of the forecasting based historical information and may increase the complexity of the forecasting of unusual incidence. The forecast model in real-time gives a small weight to the history information and a big weight to the real-time observation.
 (2)
(2)
where .
.
Figure 3 illustrates the real-time forecast model in abnormal conditions.
2.2.1. Smoothed Parameter-Gamma
Figure 4 illustrated that the value of gamma for real-time forecasting is closed to 0.9885.
2.2.2. Section Mutual Influence
In the real-time forecasting we take into consideration the effect of the upstream (UP) and downstream (DS).
 (3)
(3)
where
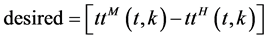
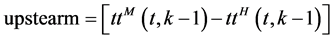

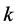 is the desired section,
is the desired section,  is the upstream section
is the upstream section  is the downstream section.
is the downstream section.

Figure 3. Real-time forecast.

Figure 4. Smoothed parameter gamma.
2.3. Accident Detection Strategy
The performance of an incident detection system is determined on two levels: data collection and data processing. Data collection refers to the detection/sense/surveillance technologies that are used to obtain traffic flow data. Data processing refers to the algorithms used for detecting and classifying incidents through analyzing the traffic parameters from detectors or sensors for the purpose of alerting observers of the occurrence, severity, and location of an incident. The hybrid of data collection strategies and data processing methodologies results in a variety of solutions for incident detection. The main task of the proposed accident detection (AD) algorithm is to identify and distinguish different traffic modes. It depends on an upstream occupation increase and a downstream occupation decrease at the level of loop detector where an incident happened. This algorithm compares a value of a traffic flow parameter with a known value. The algorithm trusts that an upstream occupation will increase and downstream occupation will decrease where an incident happened. In traffic incident detection, a time sequence is used to describe a traffic state. When a current measured value is deviated from the output of the algorithm seriously, the algorithm will think that an incident has occurred. The time sequence analytic algorithms include a moving average algorithm, an exponential smoothing algorithm.
● The accident characterized by temporal variation of speed at fixed road section (location) that expressed as the coefficient of variation in speed.
● The spatial variation of speed along road sections expressed as the difference in speed between upstream and downstream location (Q).
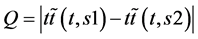 (4)
(4)
where ,
, 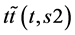 average speeds computed over period of
average speeds computed over period of  upstream and downstream of a road sections, respectively (km/h).
upstream and downstream of a road sections, respectively (km/h).
2.3.1. Incident-Influence Traffic Data
An incident occurring on section  within time interval
within time interval 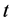 is considered to have a significant impact on traffic when traffic measurements from the upstream and downstream stations satisfy the following conditions:
is considered to have a significant impact on traffic when traffic measurements from the upstream and downstream stations satisfy the following conditions:
1) The difference between upstream speed 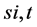 and downstream speed
and downstream speed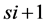 ,
, 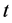 is greater than the threshold value;
is greater than the threshold value;
2) The ratio of the difference between the upstream and downstream speeds to the upstream speed 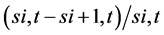 , is greater than the threshold value; and 3) The ratio of the difference between the upstream and downstream speeds to the downstream speed
, is greater than the threshold value; and 3) The ratio of the difference between the upstream and downstream speeds to the downstream speed  is greater than the threshold value.
is greater than the threshold value.
The abnormal record shows that at least 30 km/h lower traffic speed than the average speed of all records at the same time on the same day of the week. The threshold of 30km/h is a symbolic value of the smallest speed change that people would consider “abnormal”. The vehicle speed starts to decrease in upstream however the speed in downstream starts to increase.
 (5)
(5)
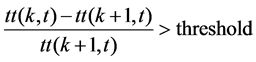 (6)
(6)
2.3.2. Real-Time Accident Detection
The travel time forecast model considers the incident and non-incident conditions. We make different between
● Accident during peak time (morning/afternoon)
● Accident during regular time
● Heavy accident
● Light accident The accident is cleared at current time t in section s, the duration is known and the speed is considered to be 30 km reduced of the average speed.
 (7)
(7)
 ,
,

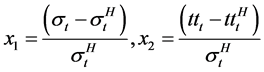 ,
,
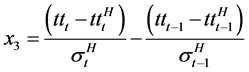 ,
,
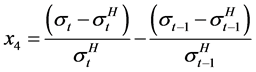
where X denotes the vector of predictor variables. β is the vector of coefficient associated with the predictor va0 riables. and can be computed according to the binary logit model. νt is the logit link function (which is a linear combination of the predictor variables).
2.4. Smoothed Parameter Optimization
To increase the exponential moving average forecast accuracy in real-time, the smoothed parameter alpha and gamma in Equation (2) should be optimized. Figure 5 illustrated the value of the optimized smoothed parameter gamma in real-time accident conditions.
Figure 6 illustrated value of the optimized smoothed
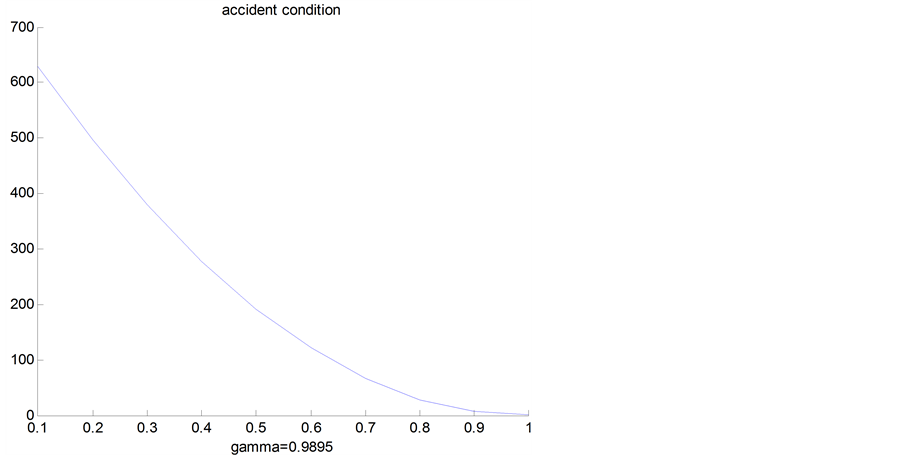
Figure 5. Gamma value AD.
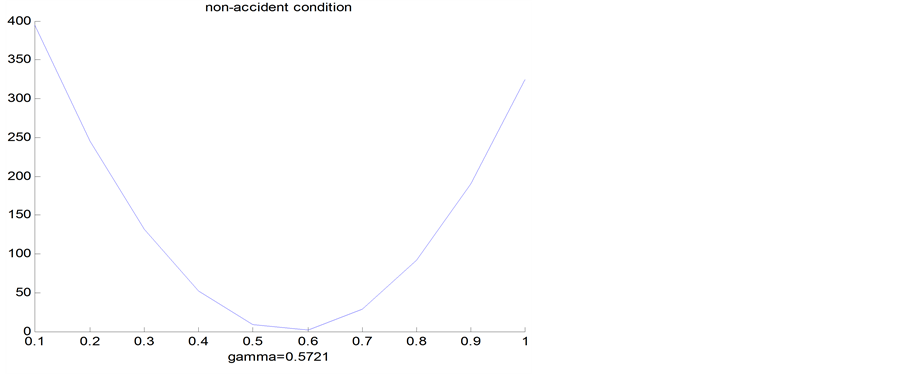
Figure 6. Gamma value in NAD.
parameter gamma in real-time non-accident conditions.
Based on Equation (7), the optimized parameters in real-time accident conditions and real-time non-accident conditions are summarized in Table1
3. Performance Analysis
There are various measures of forecasting accuracy techniques proposed in the literature [24-29]. The aim of this study is to evaluate forecast accuracy travel observations. The forecasting accuracy techniques are used to be able to select the most accurate forecast scheme. Furthermore we aim to analyze the moving average schemes, namely simple moving average, weighted moving average, and exponential moving average. The forecasting performance of the various models and the measures of the predictive effectiveness was evaluated using various summary statistics. The comparing experiments are carried out under normal traffic condition and abnormal traffic condition to evaluate the performance of four main branches of forecasting models on direct travel time data obtained by license plate matching (LPM). The MAE is a measure of overall accuracy that gives an indication of the degree of spread, where all errors are assigned equal weights. The MSE is also a measure of overall accuracy that gives an indication of the degree of spread, but here large errors are given additional weight. It is the most common measure of forecasting accuracy. Often the square root of the MSE, RMSE, is considered, since the seriousness of the forecast error is then denoted in the same dimensions as the actual and forecast values themselves. Mean square percentage error (MSPE) is the relative measure that corresponds to the MSE. The more commonly used measure is the root mean square percentage error (RMSPE). Theil’s Coefficient is another statistical measure of forecast accuracy. One specification of theil’s compares the accuracy of a forecast model to that of a naïve model. A theil’s greater than 1.0 indicates that the forecast model is worse than the naïve model; a values less than 1.0 indicates that it is better. The closer U is to 0, the better the model.
Modern vs. Traditional Traffic Data
In this section we illustrate the simulation results and analysis of the implementation of the measured traffic speeds and travel time. The information of the dual magnet loop detectors will be compared to the information that is provided from cellular phone service. Based on the WEKA platform we have carry out analysis and comparison of different Prediction schemes. WEKA (Waikato Environment for Knowledge Analysis) is a collection of machine learning algorithms for data mining tasks. WEKA contains tools for data pre-processing, classification, regression, clustering, association rules and visualization [30]. We have used the WEKA to make comparison between the following schemes:
1) Smoothed Linear Models (LM)
2) Tree Decision (TD)
3) NearestNeighbor Classifier (NN)
The comparison is focused on various statistical measurements error, mean absolute error (MAE), root mean squared error (RMSE), relative absolute error (RAE), root relative squared error (RRSE), and Theil’s coefficient. Tables 2-4 illustrate general comparison between cellular travel speed and sensor travel speed. The results of the quality measurements are summarized in Tables 2-4. Furthermore Tables 2-4 illustrate that the Nearest
Neighbor Scheme offers a clear and the best results compared to the linear model and tree decision schemes. Table 5 illustrates a comparison between the SMA, WMA, EMA.
4. Simulation Results
Results indicate that all three moving average methods, SMA, WMA and EMA, have more or less similar performance in forecasting short-term travel times. However, as one would expect the method using optimized weights produced slightly better forecasts at a higher computational cost. Quality of forecasts is diminished as the time for which forecasts are made is farther in the future. Moving average methods overestimate travel speeds in slow-downs and underestimate them when the congestion is clearing up and speeds are increasing. Figures 7-9 described the comparison between SMA, WMA and EMA based on the various statistical measurements error. Figure 10 compared the EMA to optimized EMA based on historical observations. Figures 11 and 12 showed the actual observations compared to EMA based Information and to EMA based on real-time information. Results indicate that all three moving average methods have more or less similar performance in forecasting short-term travel times. However, as one would expect the method using optimized weights produced slightly better fore
Table 5. SMA vs. WMA vs. EMA.
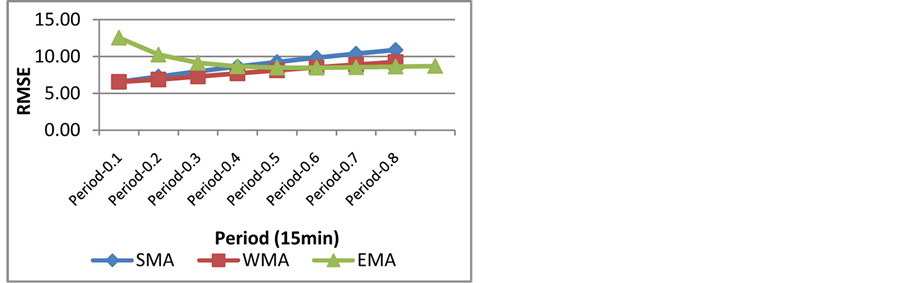
Figure 7. SMA, WMA, EMA in comparison.
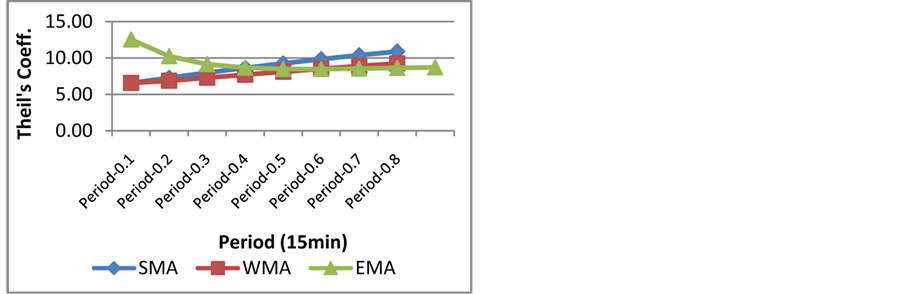
Figure 8. Theil’s coefficient.

Figure 9. MAE.
casts at a higher computational cost. Quality of forecast is diminished as the time for which forecasts are made is farther in the future. Moving average methods overestimate travel speeds in slow-downs and underestimate them when the congestion is clearing up and speeds are increasing. Figure 13 illustrated the comparison between the exponential moving average based historical information (EMA-H) and the exponential moving average based real-time information (EMA-R) compared to actual observations. EMA-H detects the abnormal conditions in travel flow traffic based pervious information that are collected in same location and at the same time. The advantage of the EMA-H is an identification of incident in flow traffic. However a repeated incident with the same characteristics in the future is not certain. Furthermore Figure 13 illustrated that EMA-R identify the incident in the flow traffic and provides incident clearness. Tables 6 and 7 illustrated the comparison between EMA based historical information and EMA based realtime in accident and in non accident conditions.
5. Conclusion
Various forecast schemes have been proposed to manage the travel flow. In order to select the fit forecast scheme, we have carried out analysis and comparison among

Figure 10. Comparison between EMA and Opt-EMA.
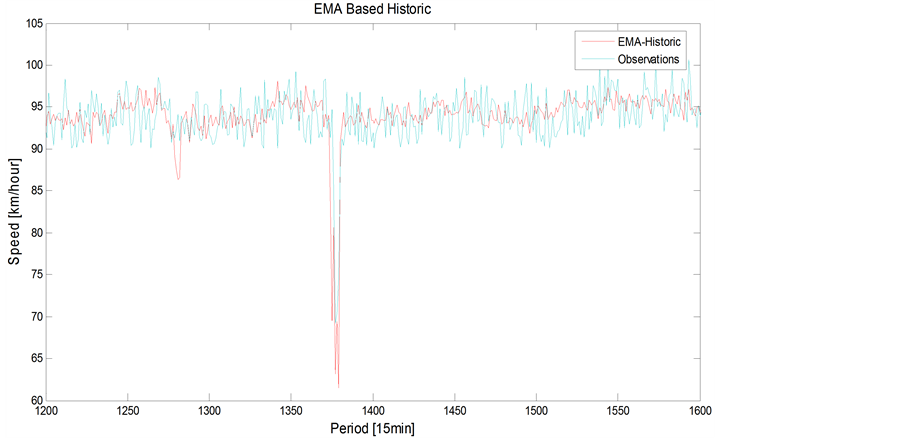
Figure 11. EMA-H vs. actual observations.
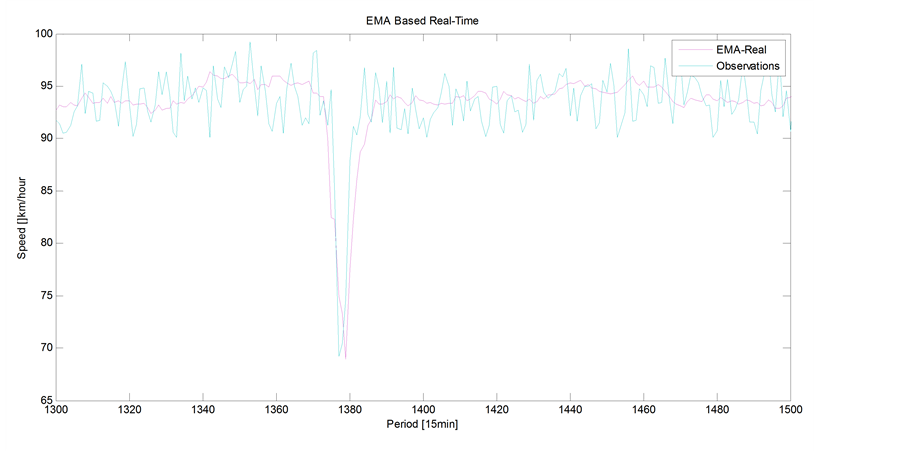
Figure 12. EMA-R vs. actual observations.

Figure 13. EMA-H, EMA-R in comparison.
different forecast schemes. In this paper, we have introduced various forecast schemes based on the historical data and real-time observations. Furthermore, in this paper, we discuss and summarize some prediction methods based on their performance analysis. We conclude that the optimized exponential moving average is the most accurate method. Moreover, the proposed algorithm has been
given the best solution for traffic travel forecast. However, the number of the road accidents increase rapidly. To reduce the incidents, a new detection scheme should be developed that takes driver’s behaviors into consideration.
REFERENCES
- J. P. Bickel, C. Chen, J. Kwon, J. Rice, V. E. Zwet and P. Varaiya, “Measuring Traffic,” Statistical Science, Vol. 22, No. 4, 2007, pp. 581-597. http://dx.doi.org/10.1214/07-STS238
- T. M. Borzacchielo, “The Use of Data from Mobile Phone Networks for Transportation Applications,” Transportation Research Board, 2010, 20 p.
- R. Chrobok, O. Kaumann, J. Wahle and M. Scheckenberg, “Three Categories of Traffic Data: Historical, Current, and Predictive,” 9th IFAC Symposium, Braunschweig, Vol. 1, 13-15 June 2000, pp. 221-226.
- R. Chrobok, O. Kaumann, J. Wahle and M. Schreckenberg, “Different Methods of Traffic Forecast Based on Real Data,” European Journal of Operational Research, Vol. 15, No. 3, 2004, pp. 558-568. http://dx.doi.org/10.1016/j.ejor.2003.08.005
- M. Alger, “Real-Time Traffic Monitoring Using Mobile Phone Data,” Proceedings on 49th European Study, 2004.
- D. Wild, “Short-Term Forecasting Based on a Transformation and Classification of Traffic Volume Time Series,” International Journal of Forecasting, Vol. 13. No. 1, 1997, pp. 63-72. http://dx.doi.org/10.1016/S0169-2070(96)00701-7
- Y. Lv and S. Tang, “Real-Time Highway Traffic Accident Prediction Based on the k-Nearest Neighbor Method,” International Conference on Measuring Technology and Mechatronics Automation, Vol. 3, 2010, pp. 547-550.
- Y. Lee and C. H. Wei, “A Computerized Feature Selection Using Genetic Algorithms to Forecast Freeway Accident Duration Times,” Computer-Aided Civil and Infrastructure Engineering, Vol. 25, No. 2, 2010, pp. 132-148. http://dx.doi.org/10.1111/j.1467-8667.2009.00626.x
- M. Martínez-Zarzuela, “Wavelet-Based Denoising for Traffic Volume Time Series Forecasting with Self-Organizing Neural Networks,” Computer-Aided Civil and Infrastructure Engineering, Vol. 25, No. 7, 2010, p. 530- 545.
- H. Nicholson and C. D. Swann, “The Prediction of Traffic Flow Volumes Based on Spectral Analysis,” Transportation Research, Vol. 8, No. 6, 1974, pp. 533-538. http://dx.doi.org/10.1016/0041-1647(74)90030-6
- I. Okutani and J. Y. Stephanedes, “Dynamic Prediction of Traffic Volume through Kalman Filtering Theory,” Transportation Research, Vol. 18B, No. 1, 1984, pp. 1-11. http://dx.doi.org/10.1016/0191-2615(84)90002-X
- B. Ronen, A. Coman and E. Schragenheim, “Peak Management,” International Journal of Production Research, Vol. 39, No. 14, 2011, pp. 3183-3193. http://dx.doi.org/10.1080/00207540110054588
- M. Sabry, H. Abd-El-Latif, S. Yousef and N. Badra, “A Time-Series Forecasting of Average Daily Traffic Volume,” Australian Journal of Basic and Applied Sciences, Vol. 1, No. 4, 2007, pp. 386-394.
- M. Sabry, H. Abd-El-Latif and N. Badra, “Comparison between Regression and Arima Models in Forecasting Traffic Volume,” Australian Journal of Basic and Applied Sciences, Vol. 1, No. 2, 2007, pp. 126-136.
- A. Stathopoulos, L. Dimitriou and T. Tsekeris, “Fuzzy Modeling Approach for Combined Forecasting of Urban Traffic Flow,” Computer-Aided Civil and Infrastructure Engineering, Vol. 23, No. 7, 2008, pp. 521-535. http://dx.doi.org/10.1111/j.1467-8667.2008.00558.x
- Y. J. Stephanedes, P. G. Michalopoulos and R. A. Plum, “Improved Estimation of Traffic Flow for Real-Time Control,” Transportation Research Record, Vol. 795, 1981, pp. 28-39.
- H. Tu, H. Van Lint and H. Van Zuylen, “The Effects of Traffic Accidents on Travel Time Reliability,” IEEE Conference on Intelligent Transportation Systems, Beijing, 12-15 October 2008, pp. 79-84.
- E. I. Vlahogianni, M. G. Karlaftis and J. C. Golias, “Temporal Evolution of Short-Term Urban Traffic Flow: A Non-Linear Dynamics Approach,” Computer-Aided Civil and Infrastructure Engineering, Vol. 23, No. 7, 2008, pp. 536-548.
- Z. Wang and P. Murray-Tuite, “Modeling Incident-Related Traffic and Estimating Travel Time with a Cellular Automaton Model,” Transportation Research Board, 2010, 21 p.
- M. S. Ahmed and A. R. Cook, “Analysis of Freeway Traffic Time-Series Data by Using Box-Jenkins Techniques,” Transportation Research Record, Vol. 722, 1997, pp. 1-9.
- J. Andrada-Felix and F. Fernandez-Rodriguez, “Improving Moving Average Trading Rules with Boosting and Statistical Learning Methods,” Journal of Forecasting, Vol. 27, No. 5, 2008, pp. 433-449. http://dx.doi.org/10.1002/for.1068
- R. R. Andrawis and F. A. Atiya, “A New Bayesian Formulation for Holt’s Exponential Smoothing,” Journal of Forecasting, Vol. 28, No. 3, 2009, pp. 218-234. http://dx.doi.org/10.1002/for.1094
- A. Guin, “Travel Time Prediction using a Seasonal Autoregressive Integrated Moving Average Time Series Model,” Proceedings of the IEEE Intelligent Transportation Systems Conference, Toronto, 17-20 September 2006, pp. 493-498.
- H. Jo, B. Lee, Y.-C. Na, H. Lee and B. Oh, “Prioritized Traffic Information Delivery Based on Historical Data Analysis,” Proceedings of the 2007 IEEE Intelligence Transportation Systems Conference, Seattle, 30 September-3 October 2007, pp. 568-573. http://dx.doi.org/10.1109/ITSC.2007.4357758
- A. Karim and H. Adeli, “Fast Automatic Incident Detection on Urban and Rural Freeways Using Wavelet Energy Algorithm,” Journal of Transportation Engineering, ASCE, Vol. 129, No. 1, 2003, pp. 57-68. http://dx.doi.org/10.1061/(ASCE)0733-947X(2003)129:1(57)
- H. Lee, N. K. Chowdhury and J. Chang, “A New Travel Time Prediction Method for Intelligent Transportation Systems” Springer-Verlag, Berlin, 2008, pp. 473-483.
- J. Xia, “Predicting Freeway Travel Time Under Incident Condition,” Transportation Research Record: Journal of the Transportation Research Board, 2010, pp. 58-66.
- X. Q. Zhao, R. M. Li and X. X. Yu, “Incident Duration Model on Urban Freeways Based on Classification and Regression Tree” 2nd International Conference on Intelligent Computation Technology and Automation, Changsha, 10-11 October 2009, pp. 625-628.
- X. Zheng and M. Liu, “An Overview of Accident Forecasting Methodologies,” Journal of Loss Prevention in the Process Industries, Vol. 22, No. 4, 2009, pp. 484-491. http://dx.doi.org/10.1016/j.jlp.2009.03.005
- J. Han, and M. Kamber, “Data Mining: Concepts and Techniques,” 2nd Edition, Morgan Kaufmann, San Francisco, 2006.


