Journal of Signal and Information Processing
Vol.06 No.04(2015), Article ID:61498,11 pages
10.4236/jsip.2015.64025
Nonparametric Spectral Estimation Technique to Estimate Dominant Frequency for Atrial Fibrillation Detection
Shafa-at Ali Sheikh1, Aftab Zafar Majoka2, Khalil Ur Rehman2, Nauman Razzaq1, Tahir Zaidi1
1Department of Electrical Engineering, College of E&ME, National University of Sciences and Technology (NUST), Rawalpindi, Pakistan
2Department of Electrical and Computer Engineering, CASE, University of Engineering and Technology, Taxila, Islamabad, Pakistan
Copyright © 2015 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).


Received 27 September 2015; accepted 23 November 2015; published 26 November 2015

ABSTRACT
Atrial fibrillation (Afib) is related with heart failure, stroke, and high mortality rates. In frequency domain analysis, pre-requisite for Afib detection has been the estimation of reliable dominant frequency (DF) of atrial signals via different spectral estimation techniques. DF further characterizes Afib, and helps in its treatment. This paper aims at finding the most appropriate nonparametric FFT-based spectral estimation technique to estimate reliable DF for Afib detection. In this work, real-time intra-atrial electrograms have been acquired and pre-processed for frequency analysis. DF is estimated via Bartlett using Hanning window, and Welch methods. Regularity index (RI), a parameter to ensure reliability of DF, is calculated using Simpson 3/8 and Trapezoidal rules. The best method is declared based upon high accuracy of Afib detection using reliable DF. On comparison, Welch method is found to be more appropriate to estimate reliable DF for Afib detection with 98% accuracy.
Keywords:
Atrial Fibrillation, Dominant Frequency, Regularity Index, Nonparametric Spectral Estimation Techniques, Welch Method

1. Introduction
Atrial fibrillation (Afib) is a supra ventricular tachycardia (SVT) in which the pacemaker activity of the sinoatrial node is overwhelmed by disorganized electrical impulses, causing rapid and irregular quivering of the atria. Atrial cells will fire at rates of about 350 - 600 bpm. Reference [1] was amongst the pioneers to propose 3- fold theory to explain Afib mechanism. Multiple wavelet hypotheses were proposed by [2] , and verified by [3] . Reference [4] attained the breakthrough by identifying Afib initiation areas in pulmonary veins. All these models indicated that although Afib appears to be an irregular arrhythmia, it follows a definite pattern of initiation and maintenance [5] . Therefore, researchers preferred frequency domain analysis over time domain analysis to detect: 1) Afib, 2) areas of rapid activations, 3) differences in pathophysiology, and 4) changes in rate as a result of interventions. For frequency domain analysis, the pre-requisite for Afib detection and its further analysis has been the estimation of reliable dominant frequency (DF) using different parametric and nonparametric spectral estimation techniques [6] .
Parametric spectral estimation techniques try to fit a parametric model to signal by minimizing certain cost function. The model order is not known in practice. An underestimation of the model order results in missing of signal poles thus reducing the resolution and causing some harmonic components to be unidentifiable. An overestimation of model order produces poles linked to the noise as well, which makes noise more prominent in spectrum by creating false peaks.
Nonparametric spectral estimation techniques do not make any assumptions on data-generating process or model. Also, the nonparametric Fast Fourier Transform (FFT) based spectral estimation techniques are more time-efficient than the parametric spectral estimation technique for real-time applications (e.g. to minimize the duration of catheter deployment) [7] . Popular nonparametric FFT-based spectral estimation techniques used for DF estimation have been: 1) periodogram, 2) modified periodogram, 3) Bartlett, and 4) Welch.
Periodogram method (without windowing) has been used by [8] -[12] . Modified periodogram method, using Hanning/Hamming windows, has been applied by [13] -[15] . However, the issue of bias and variance with periodogram and modified periodogram methods affects the quality of these spectral estimators [16] . Reference [17] suggested the Bartlett method with Hanning window to minimize the issue of bias and variance. Welch method has been applied by [18] -[20] .
DF is the frequency containing maximum power [21] . Estimation of the local atrial activation rate in AF is the key advantage of DF analysis [22] . For Afib, the DF lies in the range of 3 - 12 Hz [21] -[24] . For periodic activations, e.g. Normal Sinus Rhythm (NSR), DF gives the robust estimation of activation rate. However, for irregular activation like Afib, the estimation may not be as robust. Therefore, DF analysis for Afib is built upon selection of the lowest-noise signal. Regularity index (RI), defined as “ratio of the power spectral area under the DF and its harmonics divided by the total spectral area” has been used to ensure reliability of DF [6] -[20] . Mostly, DF with RI > 0.2 has been considered reliable for Afib detection and its further analysis [25] [26] .
Different researchers have used different nonparametric FFT-based spectral estimation techniques (periodogram, modified periodogram, Bartlett, and Welch) for DF estimation to carry out Afib detection/analysis [6] - [26] . No study has been carried to find out the most appropriate nonparametric FFT-based spectral estimation technique. Also, no details have ever been mentioned regarding calculation of power spectral areas, which are required for RI computation.
In this paper, the objective is to find the most appropriate nonparametric FFT-based spectral estimation technique to estimate reliable DF for Afib detection. As periodogram and modified periodogram are inconsistent spectral estimators and yield fluctuating estimates from successive realizations [27] , Bartlett method [28] using Hanning window, as suggested by [17] , and Welch spectral estimation method [29] are compared. Also, power spectral areas required for RI have been calculated using numerical analysis.
This paper is organized in the following way. The detailed description of the signal processing steps and algorithms is given in Section 2. Section 3 discusses the results. Limitations and conclusion/future recommendations related to this research work are highlighted in Section 4 and Section 5 respectively.
2. Methodology
2.1. Overview
In this work, ICEGMs for Afib and non-Afib (NSR) cases have been acquired from High Right Atrium (HRA) and Superior Vena Cava (SVC) for frequency domain analysis. ICEGMs are recorded using bipolar catheters with minimum inter electrode spacing (IES), which eliminated the need for cancellation of far field ventricular activity [30] . Pre-processing steps similar to [31] with addition of zero padding for better frequency resolution have been used. DF has been calculated using both Bartlett with Hanning window and Welch methods. RI is calculated using Simpson 3/8 and Trapezoidal rules [32] . Afib detection algorithm has been applied to find out Afib and non-Afib (NSR) cases. An overview of methodology is depicted in Figure 1.
2.2. Data Set and Signal Acquisition
The data set consists of ICEGMs obtained from Armed Forces Institute of Cardiology (AFIC), Rawalpindi, Pakistan, and online MIT Physionet database [33] . The study protocol has been approved by local institutional review board.
AFIC data set consists of ICEGMs for both Afib and non-Afib (NSR) cases from de identified patients. The data has been recorded from 10 patients using quadripolar catheter with 2-5-2 mm IES at sampling rate of 2000 hertz. To avoid far field ventricular activity, ICEGMs from HRA Distal catheter have been used for analysis. HRA Distal catheter configuration is shown in Figure 2.
MIT Physionet data consists of ICEGMs for Afib cases from de identified patients. The data has been recorded from the right atria of 8 patients using decapolar catheter with 2-5-2 mm IES at sampling rate of 1000 hertz. To avoid far field ventricular activity, ICEGMs extracted from catheters CS 12 and CS 34 (close to annulus of SVC) have been used for further analysis in this paper. Catheter configuration for MIT Physionet data is depicted in Figure 3.
Figure 1. Methodology overview.
Figure 2. Catheter configuration-AFIC data.
Figure 3. Catheter configuration-MIT Physionet data.
2.3. Signal Pre-Processing
Pre-processing of ICEGMs is carried out to obtain the signal corresponding to the local depolarization, and to restrict the frequency spectrum to physiological range. These include: 1) band pass (40 - 250 hertz) filtering using 3rd order Butterworth filter, 2) obtaining monophasic waveform by rectification and 3) low pass filtering (15 hertz) using 3rd order Butterworth filter.
2.4. Spectral Estimation Using Bartlett Method with Hanning Window
The Bartlett Method divides the signal segment of length N into K sub segments, with each sub segment having length L = N/K [23] . As suggested by [17] , the modified periodogram method is then applied to each K sub segment. The average of the resulting estimated power spectral density is taken as the estimated power spectrum. Mathematically, it is given as
 (1)
(1)
In this case, the signal segment (N) of 10 secs duration is defined as an “event”. It is further divided into non overlapping sub segments (K) of 2 secs each. Modified periodogram with Hanning window w(n) of each sub segment (k) is computed. The average of these five spectral estimates gives Bartlett spectral estimate. Frequency resolution is kept to be 0.1221 hertz. Figure 4 depicts the signal segment and sub segments for Bartlett method with Hanning window.
2.5. Spectral Estimation Using Welch Method
The Welch method eliminates the tradeoff between spectral resolution and variance in the Bartlett method by allowing the sub segments to overlap [27] . In the Welch method, the signal segment of length N is divided into K sub segments, with each sub segment having length L = N/K. The K sub segments of length L are overlapped and the modified periodogram are computed from the overlapped K sub segments. Also, the periodogram are normalized by the factor U to compensate for the loss of signal energy owing to the windowing procedure [22] . Mathematically, it is calculated as
 (2)
(2)
where D is the offset between two consecutive sub segments and U is given as
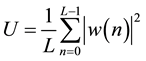 (3)
(3)
The signal segment (N) of 10 secs duration is defined as an “event”. It is divided into overlapping sub segments (K) of 2 secs each. The overlap percentage is kept to be 50% (D). Modified periodogram of each sub segment with Hanning window w(n) is taken. The average of these nine spectral estimates gives Welch spectral estimate. Frequency resolution is kept to be 0.1221 hertz. Figure 5 depicts the signal segment and sub segments for Welch method.
2.6. Dominant Frequency Estimation
The frequency having maximum peak in Power Spectral Density (PSD) estimate within range of 1 - 12 hertz is declared as DF. The maximum peak and the peaks of up to three harmonics (if exists) are found for both methods.
Figure 4. Signal segment and sub segments for Bartlett method with Hanning window.
Figure 5. Signal segment and sub segments for Welch method.
2.7. Calculation of Regularity Index (RI)
To ensure the reliability of DF, RI is computed by dividing the spectral area under DF and its harmonics within approximately1 hertz base by the spectral area for 3 - 12 hertz. The spectral area under curve is computed using Simpson 3/8 and Trapezoidal rules by using algorithm as depicted in Figure 6.
2.8. Afib Detection Algorithm
Afib detection algorithm is based on DF and RI. Figure 7 depicts the detection algorithm for Afib. After ICEGMs pre-processing, spectral estimate of the signal have been found using both Bartlett (with Hanning window) and Welch methods. Maximum peak in the range of 1 to 12 hertz has been found and declared as DF. For DF less than 3 hertz or greater than 12 hertz, RI is not calculated. For DF between 3 to 12 hertz, peaks of up to three harmonics (if exists) are also found. RI is computed to ensure reliability of DF between 3 - 12 hertz.
Afib is said to be detected if DF is in range of 3 - 12 hertz, and RI is greater than 0.2. The event is declared as non-Afib for following: 1) DF is less than 3 hertz or greater than 12 hertz, and 2) DF is between 3 - 12 hertz, but RI is less than 0.2.
3. Results and Discussions
In this work, 2500 events (2000-Afib and 500-non-Afib) have been tested by Afib detection algorithm using Bartlett (with Hanning window) and Welch methods. All these events have been marked as Afib and non-Afib by the doctors for comparison and validation of the algorithm.
3.1. Afib Event-I-Detection by Both Bartlett (Using Hanning Window) and Welch Method
In this Afib event, Afib has been detected by both Bartlett (using Hanning window) and Welch methods. Figure 8 depicts the pre-processing steps of ICEGMs. Figure 8(a) presents the ICEGMs recorded using catheters. These ICEGMs have been filtered using 3rd order band pass Butterworth filter so as to accentuate signal corresponding to local depolarization (see Figure 8(b)). Figure 8(c) depicts the absolute value of band pass filtered signal. The rectification has been performed to transform biphasic waveform into monophasic waveform. Figure 8(d) shows the low pass rectified band pass ICEGMs. Low pass filtering (LPF) with cut off frequency of 15 hertz has been carried out to limit the frequency spectrum to physiological range.
PSD for the signal depicted in Figure 8(d) has been computed using both Bartlett (with Hanning window) and Welch methods. PSD comparison is shown in Figure 9. For both methods, DF (maximum peak) turned out to be 6.1 hertz and RI was 0.50. The Afib detection algorithm has successfully declared the event as Afib for both spectral estimation techniques.
3.2. Afib Event-II-Detection by Welch Method Only
In this Afib event, Welch method has been successful in detecting Afib, however, Bartlett method (using Hanning window) declared it as non-Afib. Same pre-processing steps as of Figure 8 have been applied to ICEGMs. PSD has been computed using both Bartlett (using Hanning window) and Welch methods. On PSD comparison, as depicted in Figure 10, Welch PSD has DF (maximum peak) at 5 hertz with RI = 0.23; however, Bartlett PSD has DF (maximum peak) at 4.64 hertz with RI = 0.18. Although, DF using Bartlett method is within range of 3 - 12 hertz, however, RI is less than 0.2. This indicates that sufficient power is not contained by the peak frequency so as to qualify it as reliable DF. The Afib Detection Algorithm has successfully declared the event as Afib for
Figure 6. Algorithm to find area under curve using numerical techniques.
Figure 7. Afib detection algorithm.
Figure 8. (a) ICEGMs recorded using catheters; (b) Band passed ICEGMS; (c) Rectified band passed ICEGMS; (d) Low passed rectified band passed ICEGMS.
Welch method only.
3.3. Non-Afib Event-Detection by Both Bartlett (Using Hanning Window) and Welch Method
In this non-Afib event, NSR ICEGMs have been tested using both spectral estimation techniques. Both methods give same DF values which remained within range of 1 - 2 hertz. The Afib detection algorithm declared all such events as non-Afib for both Bartlett (using Hanning window) and Welch methods with 100% accuracy.
Figure 9. Power spectral density comparison.
Figure 10. Power spectral density comparison.
3.4. Analysis
For NSR, the Afib detection algorithm has been 100% accurate for either of the spectral estimation techniques. The reason for high accuracy and precision is the inherent periodicity of NSR. The frequency of regular pattern of NSR waveforms has been accurately estimated by both spectral estimation techniques.
For Afib events, it is found that Welch method has more accurately detected Afib events with 98% accuracy; however, Bartlett method using hanning window has an accuracy of 90%. Table 1 and Table 2 depict the range of DF and RI for both methods. It is evident that for Bartlett method (using Hanning window) DF falls within
Table 1. DF range for Bartlett and Welch methods.
Table 2. RI range for Bartlett and Welch methods.
range of 3.42 - 11.47 hertz with RI range 0.15 - 0.73. However, for Welch method the DF ranges between 3.42 - 9.52 hertz with RI range of 0.18 - 0.70.
The reasons for high accuracy of Welch method are: 1) variance of Welch method is less than that of Bartlett method, 2) averaging nine overlapped spectral estimates for Welch method in comparison of five nonoverlapped spectral estimates of Bartlett method helped in reduction of estimation error, and 3) reduction is estimation error helped to reproduce reliable DF more closer to the local activation rate.
4. Limitation
In this work, ICEGMs for analysis have been acquired from HRA and SVC only. ECG signals, ICEGMs from left atrium, and ICEGMs from other locations of right atrium have not been studied in this paper; however, this limitation does not affect the accuracy of this research work. To address the limitation, the atrial signals can be extracted from ECG/ICEGMs, and same algorithm can be applied on extracted atrial signal for estimation of DF.
5. Conclusion
Clinical applicability of frequency domain analysis for Afib has been shown by a number of researchers. However, no study has been carried out to standardize the nonparametric FFT-based spectral estimation technique for estimation of reliable DF used for Afib detection. Periodogram and modified periodogram spectral estimators are inconsistent, and carry a greater degree of estimation error. In this work, comparison of Bartlett method (with Hanning window) and Welch method is carried out. Welch method is found to be more accurate because of its better statistical properties and can be standardized not only for Afib detection but also for other frequency domain analysis like detection of areas of rapid activations, differences in pathophysiology, and changes in rate as a result of interventions. The approach presented in this paper can be modified and applied to ECG signals, ICEGMs from left atrium, and ICEGMs from other locations of right atrium to extend its applicability.
Acknowledgements
The authors wish to thank AFIC, Rawalpindi, Pakistan for their support during the course of this research, and ICT R & D Fund, Pakistan for providing the funding for this work.
Conflict of Interest
The authors declare that they have no conflict of interest.
Cite this paper
Shafa-at AliSheikh,Aftab ZafarMajoka,Khalil UrRehman,NaumanRazzaq,TahirZaidi, (2015) Nonparametric Spectral Estimation Technique to Estimate Dominant Frequency for Atrial Fibrillation Detection. Journal of Signal and Information Processing,06,266-276. doi: 10.4236/jsip.2015.64025
References
- 1. Garrey, W.E. (1924) Auricular Fibrillation. Physiological Reviews, 4, 215-250.
- 2. Moe, G.K. and Abildskov, J.A. (1958) Atrial Fibrillation as a Self-Sustaining Arrhythmia Independent of Focal Discharges. American Heart Journal, 58, 59-70.
- 3. Allessie, M.A., Lammers, W.J.E.P., Bonke, F.I.M. and Hollen, S.J. (1985) Experimental Evaluation of Moe’s Multiple Wavelet Hypothesis of Atrial Fibrillation. Cardiac Electrophysiology and Arrhythmias, 265-275.
- 4. Ha?ssaguerre, M., Ja?s, P. and Shah, D.C. (1998) Spontaneous Initiation of Atrial Fibrillation by Ectopic Beats Originating in the Pulmonary Veins. New England Journal of Medicine, 339, 659-666.
http://dx.doi.org/10.1056/NEJM199809033391003 - 5. Nademanee, K., McKenzie, J., Kosar, E., Schwab, M., Sunsaneewitayakul, B., Vasavakul, T., Khunnawat, C. and Ngarmukos, T. (2004) A New Approach for Catheter Ablation of Atrial Fibrillation: Mapping of the Electrophysiologic Substrate. Journal of the American College of Cardiology, 43, 2044-2053.
http://dx.doi.org/10.1016/j.jacc.2003.12.054 - 6. Ng, J. and Goldberger, J.J. (2007) Understanding and Interpreting Dominant Frequency Analysis of AF Electrograms. Journal of Cardiovascular Electrophysiology, 18, 680-685.
http://dx.doi.org/10.1111/j.1540-8167.2007.00832.x - 7. Ahmad, A., Schlindwein, F.S. and Ng, G.A. (2010) Comparison of Computation Time for Estimation of Dominant Frequency of Atrial Electrograms: Fast Fourier Transform, Blackman Tukey, Autoregressive and Multiple Signal Classification. Journal of Biomedical Science and Engineering, 3, 843-847.
http://dx.doi.org/10.4236/jbise.2010.39114 - 8. Skanes, A.C., Mandapati, R., Berenfeld, O., Davidenko, J.M. and Jalife, J. (1998) Spatiotemporal Periodicity during Atrial Fibrillation in the Isolated Sheep Heart. Circulation, 98, 1236-1248.
http://dx.doi.org/10.1161/01.CIR.98.12.1236 - 9. Raine, D., Langley, P., Murray, A., Dunuwille, A. and Bourke, J.P. (2004) Surface Atrial Frequency Analysis in Patients with Atrial Fibrillation: A Tool for Evaluating the Effects of Intervention. Journal of Cardiovascular Electrophysiology, 15, 1021-1026.
http://dx.doi.org/10.1046/j.1540-8167.2004.04032.x - 10. Mansour, M., Mandapati, R., Berenfeld, O., Chen, J., Samie, F.H. and Jalife, J. (2001) Left-to-Right Gradient of Atrial Frequencies during Acute Atrial Fibrillation in the Isolated Sheep Heart. Circulation, 103, 2631-2636.
http://dx.doi.org/10.1161/01.CIR.103.21.2631 - 11. Lazar, S., Dixit, S., Marchlinski, F.E., Callans, D.J. and Gerstenfeld, E.P. (2004) Presence of Left-to-Right Atrial Frequency Gradient in Paroxysmal but Not Persistent Atrial Fibrillation in Humans. Circulation, 110, 3181-3186.
http://dx.doi.org/10.1161/01.CIR.0000147279.91094.5E - 12. Yoshida, K., Ogata, K., Inaba, T., Nakazawa, Y., Ito, Y., Yamaguchi, I., Kandori, A. and Aonuma, K. (2015) Ability of Magnetocardiography to Detect Regional Dominant Frequencies of Atrial Fibrillation. Journal of Arrhythmia. (In Press)
http://dx.doi.org/10.1016/j.joa.2015.05.003 - 13. Sahadevan, J., Ryu, K., Peltz, L., Khrestian, C.M., Stewart, R.W., Markowitz, A.H. and Waldo, A.L. (2004) Epicardial Mapping of Chronic Atrial Fibrillation in Patients: Preliminary Observations. Circulation, 110, 3293-3299.
http://dx.doi.org/10.1161/01.CIR.0000147781.02738.13 - 14. Sanders, P., Berenfeld, O. and Hocini, M. (2005) Spectral Analysis Identifies Sites of High-Frequency Activity Maintaining Atrial Fibrillation in Humans. Circulation, 112, 789-797.
http://dx.doi.org/10.1161/CIRCULATIONAHA.104.517011 - 15. Matsuo, S., Yamane, T., Date, T., Tokutake, K.-I., Hioki, M., Ito, K., Narui, R., Tanigawa, S.-I., Tokuda, M., Yamashita, S., Inada, K., Minai, K., Komukai, K., Sugimoto, K.-I. and Yoshimura, M. (2012) Real-Time Dominant Frequency Analysis of the Pulmonary Vein in Patients with Paroxysmal Atrial Fibrillation. Pacing and Clinical Electrophysiolog, 35, 28-37.
http://dx.doi.org/10.1111/j.1540-8159.2011.03259.x - 16. Houben, R.P.M. and Allessie, M.A. (2007) Processing of Intracardiac Electrograms in Atrial Fibrillation; Diagnosis of Electropathological Substrate of AF. IEEE Engineering in Medicine and Biology Magazine, 25, 40-51.
http://dx.doi.org/10.1109/EMB-M.2006.250507 - 17. Ng, J., Kadish, A.H. and Goldberger, J.J. (2007) Technical Considerations for Dominant Frequency Analysis. Journal of Cardiovascular Electrophysiology, 18, 757-763.
http://dx.doi.org/10.1111/j.1540-8167.2007.00810.x - 18. Marco, L.Y.D., Raine, D., Bourke, J.P. and Langley, P. (2014) Atrial Fibrillation Type Characterization and Catheter Ablation Acute Outcome Prediction: Comparative Analysis of Spectral and Nonlinear Indices from Right Atrium Electrograms. Computing in Cardiology, 41, 817-820.
- 19. Salinet, J.L., Tuan, J.H., Sandilands, A.J., Stafford, P.J., Schlindwein, F.S. and Ng, G.A. (2014) Distinctive Patterns of DF Trajectory Behavior in Drug-Refractory Persistent AF: Preliminary Characterization of Spatio-Temporal Instability. Journal of Cardiovascular Electrophysiology, 25, 371-379.
http://dx.doi.org/10.1111/jce.12331 - 20. Cervigón, R., Moreno, J., García-Quintanilla, J., Pérez-Villacastín, J., Millet, J. and Castells, F. (2014) Frequency Spectrum Correlation along Atria to Study Atrial Fibrillation Recurrence. Computing in Cardiology, 41, 1125-1128.
- 21. Tsai, W.-C. and Lin, Y.-J. (2012) The Frequency Analysis and the Atrial Fibrillation. Journal of Biocatalysis & Biotransformation, 1, 1-2.
- 22. Traykov, V.B., Pap, R. and Sághy, L. (2012) Frequency Domain Mapping of Atrial Fibrillation—Methodology, Experimental Data and Clinical Implications. Current Cardiology Reviews, 8, 231-238.
http://dx.doi.org/10.2174/157340312803217229 - 23. Lin, Y.-J., Tai, C.-T., Kao, T., Tso, H.-W. and Higa, S. (2006) Frequency Analysis in Different Types of Atrial Fibrillation. Journal of the American College of Cardiology, 47, 1401-1407.
http://dx.doi.org/10.1016/j.jacc.2005.10.071 - 24. Arenal, A., Datino, T., Atea, L., Atienza, F., González-Torrecilla, E., Almendral, J., Castilla, L., Sánchez, P.L. and Fernández-Aviles, F. (2009) Dominant Frequency Differences in Atrial Fibrillation Patients with and without Left Ventricular Systolic Dysfunction. Europace, 11, 450-457.
http://dx.doi.org/10.1093/europace/eup053 - 25. Everett, T.H., Akar, J.G., Kok, L.C., Moorman, J.R. and Haines, D.E. (2010) Use of Global Atrial Fibrillation to Optimize the Success of Burst Pace Termination. Journal of the American College of Cardiology, 40, 1831-1840.
http://dx.doi.org/10.1016/S0735-1097(02)02476-2 - 26. Atienza, F., Almendral, J., Moreno, J., Vaidyanathan, R., Talkachou, A., Kalifa, J., Arenal, A., Villacastín, J.P., Torrecilla, E.G., Sánchez, A., Ploutz-Snyder, R., Jalife, J. and Berenfeld, O. (2006) Activation of Inward Rectifier Potassium Channels Accelerates Atrial Fibrillation in Humans: Evidence for a Reentrant Mechanism. Circulation, 114, 2434-2442.
http://dx.doi.org/10.1161/CIRCULATIONAHA.106.633735 - 27. Ifeachor, E.C. and Jervis, B.W. (1993) Digital Signal Processing: A Practical Approach. Pearson Education Ltd., Delhi.
- 28. Bartlett, M.S. (1948) Smoothing Periodograms from Time Series with Continuous Spectra. Nature, 161, 686-687.
http://dx.doi.org/10.1038/161686a0 - 29. Welch, P. (1967) The Use of Fast Fourier Transform for the Estimation of Power Spectra: A Method Based on Time Averaging Over Short, Modified Periodograms. IEEE Transactions on Audio and Electroacoustics, 15, 70-73.
http://dx.doi.org/10.1109/TAU.1967.1161901 - 30. Nagashima, K., Okumura, Y., Watanabe, I., Nakai, T., Ohkubo, K., Kofune, T., Kofune, M., Mano, H., Sonoda, K. and Hirayama, A. (2012) Effects of Inter-Electrode Spacing on Complex Fractionated Atrial Electrograms and Dominant Frequency Detection. Journal of Interventional Cardiac Electrophysiology, 34, 51-57.
http://dx.doi.org/10.1007/s10840-011-9654-1 - 31. Botteron, G.W. and Smith, J.M. (1995) A Technique for Measurement of the Extent of Spatial Organization of Atrial Activation during Atrial Fibrillation in the Intact Human Heart. IEEE Transactions on Biomedical Engineering, 42, 579-586.
http://dx.doi.org/10.1109/10.387197 - 32. Burden, R.L. and Faires, J.D. (2011) Numerical Analysis. Cengage Learning, Boston.
- 33. Goldberger, A.L., Amaral, L.A.N., Glass, L., Hausdorff, J.M., Ivanov, P.C., Mark, R.G., Mietus, J.E., Moody, G.B., Peng, C.-K. and Stanley, H.E. (2000) PhysioBank, PhysioToolkit, and PhysioNet: Components of a New Research Resource for Complex Physiologic Signals. Circulation, 101, e215-e220.
http://circ.ahajournals.org/cgi/content/full/101/23/e215
http://dx.doi.org/10.1161/01.cir.101.23.e215












