Journal of Signal and Information Processing
Vol.06 No.01(2015), Article ID:53580,18 pages
10.4236/jsip.2015.61002
Robust Non-Coherent Demodulation Scheme for Bluetooth Voice Transmission Using Linear, Extended, and Unscented Kalman Filtering
Ali S. Alghamdi1,2,3, Mahdi N. Ali4, Mohamed A. Zohdy1
1Electrical and Computer Engineering Department, Oakland University, Rochester, MI, USA
2Saudi Red Crescent Authority, Riyadh, Saudi Arabia
3Ministry of Higher Education, Riyadh, Saudi Arabia
4Hyundai Motor Company, Superior Township, MI, USA
Email: asalgham@oakland.edu, zohdyma@oakland.edu, mali@hatci.com
Copyright © 2015 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 10 January 2015; accepted 26 January 2015; published 28 January 2015
ABSTRACT
This paper presents a novel and cost effective method to be used in the optimization of the Gaussian Frequency Shift Keying (GFSK) at the receiver of the Bluetooth communication system. The proposed method enhances the performance of the noncoherent demodulation schemes by improving the Bit Error Rate (BER) and Frame Error Rate (FER) outcomes. Linear, Extended, and Unscented Kalman Filters are utilized in this technique. A simulation model, using Simulink, has been created to simulate the Bluetooth voice transmission system with the integrated filters. Results have shown improvements in the BER and FER, and that the Unscented Kalman Filters (UKF) have shown superior performance in comparison to the linear Kalman Filter (KF) and the Extended Kalman Filter (EKF). To the best of our knowledge, this research is the first to propose the usage of the UKF in the optimization of the Bluetooth System receivers in the presence of additive white Gaussian noise (AWGN), as well as interferences.
Keywords:
Bluetooth System Unscented Kalman Filter (UKF), Interferences, Gaussian Frequency Shift Keying (GFSK), Noncoherent Demodulation, Additive White Gaussian Noise (AWGN), Bit Error Rate (BER), Matlab Simulink

1. Introduction
In recent years, we have seen that the Bluetooth technology [1] becomes usable in diverse applications, in addition to being a standard feature in cell-phone devices. Due to its low costs, it has been used in most of the short distance communication systems, and there is a significant reason for that: the Bluetooth technology has free wireless bandwidth for short distance connection within 2.4 GHz frequencies.
The proposed method in this research is employed at the Gaussian Frequency Shift Keying (GFSK) modulation level in the physical layer of the Bluetooth system [2] . Bluetooth receivers implement on-coherent demodulation, which results in low cost products, but unreliable and poor performance in most applications. On the other hand, in order to optimize a non-coherent demodulation system, some complex Maximum Likelihood Sequence Estimators (MLSE) are used. Figure 1 shows a top level diagram of the Bluetooth system with our contribution of the robust Kalman Filter scheme. In the system block diagram, each block will be explained in detail in subsequent sections of this paper. We can see that the Kalman Filter (KF) is integrated in the receiver before the demodulation stage, so that it optimizes the detection processes. Furthermore, since we are dealing with a nonlinear system, the Extended Kalman Filter (EKF) and the Unscented Kalman Filter (UKF) are used in the optimization of the detected signals.
In 1960, Rudolf E. Kalman presented his idea of Kalman Filtering in [3] . KF is an estimator that estimates the states in linear dynamic systems by minimizing the Mean Square Error (MMSE). Kalman invented his filter based on modifying the Wiener-Kolmogorov filter, which was derived in 1940. While Wiener and Kolmogorov developed their filters based on frequency domain analysis, Kalman proposed his filter based on time domain analysis. The KF originated from Baye’s probabilistic theory, in which, if a good number of past samples are known, then the future samples can be predicted and updated based on continuously collected results. Since most practical systems in real life are nonlinear, many research methods have been proposed to modify KF to be applied to nonlinear systems. The EKF has been proposed to be used in nonlinear systems by linearizing the states and measurement variables under study. In [4] , the EKF has been used to optimize the received signal in the Bluetooth system in the presence of interferences, and produced better MSE in different Signal to Noise Ratio (SNR).
Literature [4] [5] has presented solid improvements, in which the KF proved to be useful in optimizing the Bluetooth system; however, the research in [5] investigated the performance of the system with the UKF. It concluded that the UKF produced a better outcome than the EKF. However, that paper performed the analysis without considering the interferences in the 2.4 GHz band in the AWGN. The work of this paper will continue on their work, which was listed in [4] [5] . In this research, the KF, EKF, and UKF are integrated into the Bluetooth receivers. The mathematical theory and derivation will be presented. The simulation model and results analysis will be analyzed and compared.
2. Literature Study
There has been a great deal of literature, which has focused on the performance of the Bluetooth receivers. A
Figure 1. Bluetooth system with the integrated robust Kalman Filtering technique.
significant amount of research has been performed to improve the non-coherent detection in the area of signal processing. Most of the research has developed techniques to improve the synchronization performance in low complexity demodulation schemes. The following sections describe the contributions that have been done in this related work.
Since 2003, up to the present, a GFSK has been optimized by many different techniques, which resulted in BER improvements. In [6] , the authors investigated the performance of frequency hopped on GFSK for the Rayleigh fading channel; they showed an improvement in BER over the fading channel, which was corrupted by AWGN by the pilot assisted differential detection. Meanwhile, the authors in [7] proposed a new digital receiver for a BT, where they combined a zero crossing demodulation with the de-correlating matched filter, and it also was tested on the BER performance versus , the modulation index for GFSK.
, the modulation index for GFSK.
The paper in [8] presents an improvement on the GFSK modulation method by using maximum likelihood sequence estimation (MLSE), based on a linearized model of the modulation. Furthermore, the authors were dedicated to evolving a scheme that had MLSE-oriented detection using the Viterbi equalizer considering a GFSK inherent inter symbol interference (ISI), with the channel gain sensitivity of 0 - 7 dB. In the article [9] , the author proposed a new receiver design, studying the sequence detection and discovering an algorithm, which they called non-coherent sequence detection (NSD). The new algorithm is unique in low complexity, as it operates distinctions caused by low-cost local oscillators. The NSD is combined with a forward error correction decoder, which yields optimal results in real Bluetooth devices. Another proceeding [10] developed a simulator for the Bluetooth scatternet, which had been tested in BER performance with an ad-hoc network using the ARQ scheme.
Some of these researches were proposed for the general purpose of optimization of signal detection for the GFSK modulation; hence, it can be considered for the Bluetooth systems improvement method. Digital carrier synchronization in [11] used a decision-aided data cancellation algorithm to compute the carrier frequency offset (CFO) for GFSK, where they measured the error difference due to the decision output between the
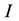 and
and
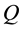 receiver channels. The CFO will be taken into account, if the orthogonal frequency division multiplexing (OFDM) multi-user’s technique is desirable, yet it is useful only for the multi-Piconet connection in a fading environment. Later on, a new optimization was published in a differential GFSK demodulator [12] . The author proposed the splitting of the transmitting data into a sequence of segments assigned different coefficients by setting up the first half of the sequence as linear and the other half as non-linear.
receiver channels. The CFO will be taken into account, if the orthogonal frequency division multiplexing (OFDM) multi-user’s technique is desirable, yet it is useful only for the multi-Piconet connection in a fading environment. Later on, a new optimization was published in a differential GFSK demodulator [12] . The author proposed the splitting of the transmitting data into a sequence of segments assigned different coefficients by setting up the first half of the sequence as linear and the other half as non-linear.
Some literature, which is the focus of our research, was published during the last four years. The article in [13] investigated the Bluetooth interference by enabling the Enhanced Data Rates (EDR) to run on three types of modulation techniques: Differential Quadratic Phase Shift Keying (π/4-DQPSK, 8-DPSK, and GFSK). Their result and analysis were impressive, because they applied to a real Bluetooth experimental application. The article produced significant results for the three types of modulations in the packet delay, which was stable and unaffected when the BER was 10−3 or higher. On the other hand, a study had been done on a similar topic in [14] , in which the authors studied the interference of 802.11b WLAN, in which they developed a new Bluetooth voice packet synchronous connection oriented with a repeated transmission (SCORT) scheme. Their analysis focused on the interferences in the 2.4 GHz frequency unlicensed bandwidth, and their application was applied in a medium access control (MAC) layer. This paper focused on the future work as it is presented in [5] , in which the authors proposed an optimization method of the GFSK and DPSK demodulation schemes using UKF, without considering the 802.11b interference factors in their work. The authors came up with an interactive Kalman Filtering technique to optimize the non-coherent GFSK and DPSK to produce better BER results. Finally, in [4] [15] -[17] , the authors made decent contributions using an EKF for GFSK, in order to estimate the phase of the signal at the receiver of the Bluetooth system, while considering the 802.11b interference factors in Gaussian noise and non-Gaussian noise environments.
3. GFSK Signal Description
The GFSK modulation method is widely used in digital communications, including Bluetooth systems. Figure 2 illustrates the GFSK modulation system, and its modulated waveform can be represented as follows [3] [5] [18] :
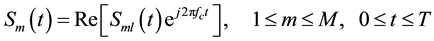 (1)
(1)
Figure 2. GFSK modulation block diagram.
 (2)
(2)
where
 (3)
(3)
Equation (2) is the formal GFSK signal generated by shifting the carrier within the amount of ,
,
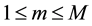 , to reflect the digital information that will be transmitted. This GFSK modulation is different from the Frequency Shift Keying (FSK), because we need to avoid using signals having large spectral side lobes. The information-bearing signal frequency modulates a signal carrier whose frequency is changed continuously. This is the result of the modulated signal, which is phase-continuous, and is called the Continuous-Phase Frequency Shift Keying (CPFSK); hence, this type of signal has memory, and the phase of the carrier is constrained to be continuous [18] .
, to reflect the digital information that will be transmitted. This GFSK modulation is different from the Frequency Shift Keying (FSK), because we need to avoid using signals having large spectral side lobes. The information-bearing signal frequency modulates a signal carrier whose frequency is changed continuously. This is the result of the modulated signal, which is phase-continuous, and is called the Continuous-Phase Frequency Shift Keying (CPFSK); hence, this type of signal has memory, and the phase of the carrier is constrained to be continuous [18] .
A complete presentation of CPFSK will start to drive the signal representation from the Pulse Amplitude Modulation (PAM):
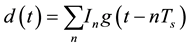 (4)
(4)
where
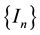 denoted the sequence of the amplitudes obtained by mapping
denoted the sequence of the amplitudes obtained by mapping
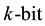 block in
block in , information symbols
, information symbols
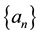 can be represented in the format of
can be represented in the format of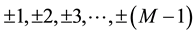 , and
, and

pulse of the amplitude


the carrier. Consequently, the complex baseband waveform


where



The



Carrying out the integral of the phase carrier in the interval



where:



The parameter



where


4. Noisy Channel
The employed channel is an additive white Gaussian noise (AWGN), which is widely and extensively used in wireless communication, especially with short distance connections [9] . The receiving signal can be represented as:

where




802.11 Interference Model
IEEE 802.11b is an exponential model developed for a 2.4 GHz indoor channel. It is used for small coverage areas, such as a Wi-Fi network inside a building. However, the channel conditions may vary with time and location, due to the environment being enclosed by walls, which still requires a power delay profile (PDP) to characterize their channel delay and power average. The channel impulse response can be calculated through the
Figure 3. Noisy channel structure.
output of a finite impulse response (FIR) filter; of course, each channel is modeled by a complex Gaussian random variable with its average power. In order to determine the maximum number of paths, we need to calculate the RMS delay


Let us consider that we have a Gaussian distribution
maximum excess delay, according to the specification of the 802.11 channels, is 10 times the RMS delay. So, the power of each channel can be represented as:

where


Figure 4 is an illustration of an example of the 802.11 indoor channel impulse response, and its power average, when

5. Non-Coherent Detection
The detection is part of the demodulation stage at the receiver side of the BT in Figure 1. In BT, we do not have a reliable receiver, or, in other words, the transmitter does not have a distinguished receiver, which has none of the transmitting signal property. Therefore, they are called a non-coherent detection, due to the invalid assumption of the signals

Obviously, Figure 5 provides a proof of our statement, when we address the GFSK modulation as a product of the periodic square signal and the Gaussian filter, so the phase increases


Figure 4. 802.11b channel impulse example with their power.
Figure 5. Phase trajectory for binary GFSK.
the real convolution of the complex baseband waveform Equation (3):

where




In this case


with the probability of transmitting



6. GFSK State Space Model
A GFSK module signal needs to be modified according to the KF procedure, because KF operates in two steps: a prediction and an update, so GFSK signals have a magnitude and a phase angle. For non-coherent detection, we proposed the phase estimation, in order to detect the information using the phase trajectory illustrated in Figure 5. Prediction and update processes have the relation between the previous phase and current phase estimations, finding the error among them, and then predicting the next phase.
GFSK Description
In the KF development procedure, the implementation took place to evaluate or estimate in two steps: predict and update. The prediction has been computed by KF to evaluate the current phase and the previous state phase, finding the error, to update the future state, using the residual calculated error. GFSKs have a magnitude and a phase angle, which are unpredictable, due to the noise effect. Our KF are involved in two states to estimate the phase





Now, our desirable result is to estimate the phase





Equation (23) shows that the system begins the module in nonlinear format, and the receiving signal can be written as:

7. State Model
By substituting Equation (26) into Equations (23) and (24), the state difference equations can be formalized as:

Noise Measurement Model
According to the non-coherent detection, the typical receiver of AWGN has a correlated process when the receiving signal is divided in two phases: in-phase and quadratic phase components, which are the more familiar phase




8. Proposed Scheme Analysis
Referring to Figure 1, the first stage at the receiver, which we have called the “Robust Kalman Filter Scheme”, yields our contributed scheme, yet we are using a KF, which is one of the adaptive filters for signal processing manner. Although in this paper we adjust our results in three types of filters: linear KF, EKF, and UKF, all of them have been extensively used in stochastic random signal processing. The result could be a rich optimization for a wireless communication connection. Moreover, the author in [5] implemented an interactive KF, using a two-modulation technique, and simultaneously concluded his article by proving the UKF had a better result, but his effort was in the system with no interference, assuming the BT system was operated in an area such as a vehicle, where there is not much 802.11b interference. Nonetheless, the authors in [4] [15] -[17] have also contributed meaningfully to the same topic, to improve the non-coherent detection for GFSK proposed in their work for the BT system, by involving 802.11b interference in their results. Hence, their efforts were published, concluding with using the EKF for the purpose of a nonlinear optimization minimizing the mean square error (MES).
Beginning with our scheme description, we are designing three types of stochastic filters, as we mentioned earlier: linear KF, EKF, and UKF, while we have fully considered the latest literature review, as applied to the BT voice transmission system [19] . Consequently, we will be presenting our schemes analysis in three sections, each one discussing the details of our filters, and Figure 6 gives an image of our robust scheme that cascaded with the demodulation stage.
Figure 6. Slave non-coherent demodulation black diagram.
In the early 1960s, R. E. Kalman considered the same problem that Wiener had dealt with. In his 1960 paper, he proposed the noise measurement to be a discrete sequence in time, applied to a continuous-time signal [20] . In addition, the KF recursive equation was treated as a computational loop between an input and an output of the dynamic system, so the loop had two major tasks: predict and update. The following is the general form of the linear KF equations [20] [21] :


where:






Now, for our system, the general Kalman state equations need to modify the base on the signal representation of GFSK, so we let




Nonetheless, we need to have



The prior (or a priori) estimate will be denoted as





8.1. Linear Kalman Filter (KF)
First of all, we have to rewrite a KF state space model, corresponding to our GFSK modulated signal, carried in the general KF format in Equations (30) and (31).


For linear estimation, we have two types of covariance matrices that need to be considered for





Corresponding to error Equation (34), the error covariance matrix is:

Now, we are looking to use the measurement


where




By substituting the Equation (36) into Equation (41), we will yield a result that has been substituted in Equa-
tion (42), and illustrate that

error . Although, from the algebraic substitutions, we will be end up with a general expression for the update er- ror covariance matrix.

Expanding Equation (43) becomes:

Optimizing





Thus, the Equation (45) gives the suitable value of


Hence, we still need to find





Back to using the error estimation Equation (34), according to Equation (44), we have:


So far, we derived the entire KF algorithm processes associated with the modulated BT system, and Figure 7 shows the block diagram of the KF algorithm to prove the statement of recursive equation.
8.2. The Extended Kalman Filter (EKF)
It was mentioned earlier, in Section 2, that [4] [15] -[17] have made meaningful contributions in the same subject that with which we are working, especially in using EKF for a non-coherent BT receiver. Furthermore, proposing an EKF for this article becomes more a matter of comparison, and some of the better achievements will be illustrated in Section 10. The EKF has been developed for nonlinear dynamic systems, and nonlinear measurement relationships, certainly, will require a linearization process for prediction and update measurements. Thus, the linearization will accommodate the general linear KF system module, so, starting with our system, we have an associated measurement relationship that may be written as [20] :


where







So, Equations (50) and (51) can be written as:


Now, we approximate the





Equation (57) is the Jacobian matrix, and it allows having the nominal trajectory of

Figure 7. Kalman recursive algorithm.


Finally, the EKF can apply to the linear KF algorithm shown in Figure 7; once the linearization process is taken care of, the sequences and the coefficients of the measurements



8.3. The Unscented Kalman Filter (UKF)
For random variables (RV), or Gaussian random variables (GRV), the UKF proposed an extension development of EKF, in particular, for nonlinear statistical estimation regarding the main principles of linear KF, which are prediction and update. Obviously, the name of UKF came after the unscented transformation (UT), which developed the solution; in another words, the UT evaluates the mean and covariance (

Assuming a nonlinear function






(i) Scaling the unscented samples:

where:

Figure 8. The principle of UT.




(ii) Transforming the unscented samples:
(iii)

(iiii)


Equations (64) and (65) describe how UT computes the mean and covariance; also, Figure 9 visualizes the UT data process. Now, it is necessary to run the linear KF through the output of UT, starting with the basic form of the linear KF dynamic system, involving the process update and measurement update.
The UKF algorithm starts from the original linear KF measurement model, and then takes inside an initial state where


Figure 9. UT mean and covariance processes.

Equations (66) and (67) are the nonlinear UKF equations with noise inputs


Initialize:


Calculating the sigma points:

Time update processes:
The prediction of UKF projects the set of samples through the nonlinear Equation (66) as


Thus, after computing the optimal mean Equation (71), and its error covariance Equation (72), we can re- sample a new sigma point for the remainder from the following relationship:

The next steps are the measurement update processes, which required the sigma points operated through the nonlinear Equation (67).





Finally, the Kalman gain



9. Simulations and Numerical Results
The BT voice transmission system has been created on Matlab/Simulink environments [19] ; the demo version has been modified for the purpose of our optimization. We set the transmitting signal power to 10 mW, which is sufficient for an indoor radius of 20 meters. The high level Simulink model is shown in Figure 10 for the BT system [19] .
Figure 11 shows the linear KF system model that has been implemented as a cascaded stage at the slave receiver side, and, as it is illustrated, it has two embedded functions: one for imaginary, and the other for real estimation. Furthermore, Figure 12 and Figure 13 will illustrate the modulation scheme for the EKF and UKF respectively, while all of the three Kalman filters have been identified in Figure 6 as a Kalman filter subsystem block.
The simulation results have been analyzed in two different aspects: Bit Error Rate (BER) and Frame Error Rate (FER). The significance of the BER shows the performance of these types of filters in BT system application, and, as a result, it is concluded that the UKF contributes the better result between the linear KF and the EKF. Moreover, the linear KF gives the worst result, which is proof of our expectation about the nonlinear propagation of the transmitting signals, because it is only suitable for linear purposes. According to the theoretical AWGN, shown in Figure 14, the UKF gave the best result at a high noise measurement, and at a low noise measurement, versus the AWGN theoretical result.
Second, in an analysis approach based on the FER, or, in other words, on a package transmitting estimation, we divide every 366 bits into a frame, or a package. The package transmitting concept was more useful on broadcasting data transmission, and, from Figure 15, where the UKF wins the computation of the three types of Kalman filters, according to expectation; the UKF will produce the best results in the matter of the FER. Nonetheless, the FER does not show a theoretical result, but the UKF in Figure 14 illustrates better than do the linear KF and the EKF.
In summary, the experiment simulation is designed and run in different SNR values to come up with the previous results shown in Figure 13, and Figure 14, and each result was computed out of 100 bits of error. Even
Figure 10. Top level Simulink Bluetooth system model.
Figure 11. Linear Kalman Filter Scheme implemented at the robust stage at the receiver of the Bluetooth.
Figure 12. Extended Kalman Filter Scheme implemented at the robust stage at the receiver of the Bluetooth.
Figure 13. Unscented Kalman Filter Scheme implemented at the robust stage at the receiver of the Bluetooth.
Figure 14. Bit Error Rate (BER).
so, the results will be summarized in Table 1, denoting the meaningful outcomes of this experiment.
10. Conclusion and Future Work
In this paper, a novel achievement has been delivered through the design of the UKF, which shows a high qual- ity for the BT system. The challenge was not only filtering a signal, but also utilizing the optimal contributions from among the related works that have been done previously. Therefore, the non-coherent GFSK has been
Figure 15. Frame Error Rate (FER).
Table 1. Summarizing the Kalman filters performance verses signal to noise ratio (SNR).
validated using the Bluetooth voice transmission model, which had already been created in Matlab/Simulink software. As a result, an improvement has been executed on the physical layer, which is where we dealt with non-coherent GFSK modulation and demodulation; definitely, our robust scheme has been designed in order to use a faster sampling rate for the execution time of the filter.
There is always room for future works in this area, and some of them are going to be our next tasks, to continue our work. One future task will be applying the same experiment from this paper to an interactive Kalman filter, where the signals have to be modulated into two different techniques simultaneously for tunable purposes. A second task will be to develop the UKF for a multi-path fading channel, which is extensively valid for the 802.11 indoor channel models. The third task will be to consider the multi-user OFDM system, which is useful for master transmitting to Piconet and scatternet; in other words, using a multi-slave receivers connection. Finally, the experiment for the in-vehicle channel mode should be created, which would be a benefit for a tremendous number of the in-vehicle multimedia applications.
Acknowledgements
I really would like to thank to Saudi Red Crescent Authority for its help in providing me the time, and the financial support, to establish my Ph.D. research.
I would also like to express my appreciation to the Saudi Arabian Cultural Mission for its infinite support, and supervising us in the United States, in order to achieve our dream.
Additionally, this research paper could not have been done without Debbie Barry, for her editing and linguistics help.
Cite this paper
Ali S.Alghamdi,Mahdi N.Ali,Mohamed A.Zohdy,11,11, (2015) Robust Non-Coherent Demodulation Scheme for Bluetooth Voice Transmission Using Linear, Extended, and Unscented Kalman Filtering. Journal of Signal and Information Processing,06,9-27. doi: 10.4236/jsip.2015.61002
References
- 1. B. S. I. Group (2014) Bluetooth SIG. Bluetooth SIG. https://www.bluetooth.org/en-us
- 2. Leon, I. and Couch, W. (2007) Digital and Analog Communication Systems. 7th Edition, Pearson Prentice Hall, Upper Saddle River.
- 3. Brown, R.G. and Hwang, P.Y. (2012) Introduction to Random Signals and Applied Kalman Filtering. 4th Edition, John Wiley & Sons, Inc., Hoboken.
- 4. Nsour, A., Abdallah, A.-S. and Zohdy, M. (2013) Phase Tracking in Bluetooth Receivers Using Extended Kalman Filtering. 3rd International Conference on Wireless Communications, Vehicular Technology, Information Theory and Aerospace & Electronic Systems (VITAE), Atlantic City, 24-27 June 2013, 1-5.
- 5. Ali, M. and Zohdy, M. (2012) Interactive Kalman Filtering for Differential and Gaussian Frequency Shift Keying Modulation with Application in Bluetooth. Journal of Signal and Information Processing, 3, 63-76. http://dx.doi.org/10.4236/jsip.2012.31009
- 6. Liu, H., Venkatesan, V., Nilsen, C., Kyker, R. and Magaña, M. (2003) Performance of Frequency Hopped Noncoherent GFSK in Correlated Rayleigh Fading Channels. ICC’03. IEEE International Conference, 11-15 May 2003, 2779-2783.
- 7. Scholand, T. and Jung, P. (2003) Novel Receiver Structure for Bluetooth Based on Modified Zero-Crossing Demodulation. Global Telecommunications Conference, GLOBECOM’03. IEEE, 1-5 December 2003, 729-733.
- 8. Lampe, L., Schober, R. and Jain, M. (2005) Noncoherent Sequence Detection Receiver for Bluetooth Systems. Selected Areas in Communications, IEEE Journal, 23, 1718-1727.
http://dx.doi.org/10.1109/JSAC.2005.853791 - 9. Roh, J.S. (2006) Performance Analysis and Evaluation of Bluetooth Networks in Wireless Channel Environment. Systems and Networks Communications, ICSNC’06, October 2006, Tahiti, 61 p.
- 10. Chang, D.-C. and Shiu, T.-H. (2006) Digital GFSK Carrier Synchronization. Circuits and Systems, APCCAS 2006, IEEE Asia Pacific, Singapore, 4-7 December 2006, 1523-1526.
- 11. Yu, B., Yang, L. and Chong, C.-C. (2011) Optimized Differential GFSK Demodulator. IEEE Transactions on Communications, 59, 1497-1501. http://dx.doi.org/10.1109/TCOMM.2011.041111.100010A
- 12. Luque, J.R., Morón, M.J. and Casilari, E. (2012) Analytical and Empirical Evaluation of the Impact of Gaussian Noise on the Modulations Employed by Bluetooth Enhanced Data Rates. EURASIP Journal on Wireless Communications and Networking, 2012, 94.
http://dx.doi.org/10.1186/1687-1499-2012-94 - 13. Mathew, A., Chandrababu, N., Elleithy, K. and Rizvi, S. (2010) Interference of 802.11B WLAN and Bluetooth: Analysis and Performance Evaluation. International Journal of Computer Networks & Communications (IJCNC), 2, 140-150.
- 14. John, P.G. and Masoud, S. (2008) Digital Communications. McGraw-Hill, New York.
- 15. Nsour, A., Abdallah, A.-S. and Zohdy, M. (2013) An Investigation into Using Kalman Filtering for Phase Estimation in Bluetooth Receivers for Gaussian and Non-Gaussian Noise. Proceedings of the 2013 IEEE International Conference on Electro/Information Technology (EIT), Rapid City, 9-11 May 2013, 1-5.
- 16. Nsour, A., Abdallah, A.-S. and Zohdy, M. (2013) GFSK Phase Estimation Using Extended Kalman Filtering for Non-Gaussian Noise. Proceedings of the Wireless Telecommunications Symposium (WTS), Phoenix, 17-19 April 2013, 1-6.
- 17. Nsour, A., Abdallah, A.-S. and Zohdy, M. (2014) Non-Coherent Detection of GFSK Using Extended Kalman Filtering for Non-Gaussian Noise. Proceedings of the Wireless Telecommunications Sym-posium (WTS), Washington DC, 9-11 April 2014, 1-6.
- 18. Mathworks, Inc. (2014) Bluetooth® Voice Transmission.
http://www.mathworks.com/help/comm/examples/bluetooth-voice-transmission.html - 19. Wan, E. and Van der Merwe, R. (2000) The Unscented Kalman Filter for Nonlinear Estimation. Proceedings of the IEEE 2000 Adaptive Systems for Signal Processing, Communications, and Control Symposium, Lake Louise, 1-4 October 2000, 153-158.
- 20. Brown, R.G. and Hwang, P.Y.C. (2012) Introduction to Random Signals and Applied Kalman Filtering. In: Brown, R.G. and Hwang, P.Y.C., Eds., Introduction to Random Signals and Applied Kalman Filtering with Matlab Exercises, 4th Edition, John Wiley & Sons, Inc., Hoboken, 141-148.
- 21. Yang, W.Y., Cho, Y.S., Choo, C.Y., Shim, J., Jeon, W.G., Kim, J., Yu, S., Park, K.W. and Wee, J. (2012) MATLAB/Simulink for Digital Signal Processing. Hongrung Publishing Company, Seoul.
- 22. Julier, S. and Uhlmann, J. (2004) Unscented Filtering and Nonlinear Estimation. Proceedings of the IEEE, 92, 401- 422.
- 23. Cho, Y.S., Kim, J., Yang, W.Y. and Kang, C.G. (2010) MIMO-OFDM Wireless Communications with MATLAB. John Wiley& Sons (Asia), Singapore.


















