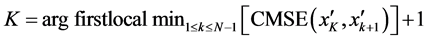Journal of Signal and Information Processing
Vol.05 No.04(2014), Article ID:50365,7 pages
10.4236/jsip.2014.54013
A De-Noising Method for Track State Detection Signal Based on EMD
Liming Li, Xiaodong Chai, Shubin Zheng, Wenfa Zhu
College of Urban Railway Transportation, Shanghai University of Engineering Science, Shanghai, China
Email: liming0028@126.com, cxdyj@163.com, zhengshubin@126.com, zhuwenfa1986@163.com
Copyright © 2014 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 14 August 2014; revised 10 September 2014; accepted 5 October 2014
ABSTRACT
In the track irregularity detection, the acceleration signals of the inertial measurement unit (IMU) output which with low frequency components and noise, this paper studied a de-noising algorithm. Based on the criterion of consecutive mean square error, a de-noising method for IMU acceleration signals based on empirical mode decomposition (EMD) was proposed. This method can divide the intrinsic mode functions (IMFs) derived from EMD into signal dominant modes and noise dominant modes, then the modes reflecting the important structures of a signal were combined together to form partially reconstructed de-noised signal. Simulations were conducted for simulated signals and a real IMU acceleration signals using this method. Experimental results indicate that this method can efficiently and adaptively remove noise, and this method can better meet the precision requirement.
Keywords:
Track Irregularity, Signal De-Noising, Empirical Mode Decomposition, Consecutive Mean Square Error

1. Introduction
Track irregularity is an important geometric parameters of reflecting the quality of the track, is to detect the quality of the track, which tracks long-wave irregularity include track vertical and the level of irregularity two aspects, as the excitation source of railway system, high and low irregularity aggravate the fluctuation of vibration of the train, and the level irregularity intensifies the sway of the train [1] [2] . Track irregularity has a great effect on train running stability and passengers ride comfort, and adverse to the driving safety, many countries in the world is to strengthen for detection of track irregularity. The current railway system mainly uses the verse sine method and the inertial reference method to measure track long-wave irregularity [3] [4] .
In using strap down inertial technology testing track irregularity, due to the track on a certain length of horizontal pendulum angle can’t be very big, the implementation of track inspection car speed is low, the inertial unit output value of the acceleration and angular velocity is small, and its output signal is very weak, and contains a certain amount of noise, easy to cause integrator saturation, thereby affects the detection accuracy of long wave irregularities [5] - [10] . This paper is based on EMD (empirical mode decomposition, the EMD) under the CMSE principles to collect inertial unit to deal with the noise signal, the experimental results show that the method can effectively suppress noise and improve the detection accuracy.
2. Empirical Mode Decomposition (EMD)
2.1. The Definition Intrinsic Mode Function
According to different signal time scale, the EMD can decompose complex signal into several intrinsic mode function (intrinsic mode function, the IMF) arranging from high to low according to the frequency, so it can be seen as based on the extremum characteristic scale for measuring signal filtering process of space and time, can use this property to filter the signal analysis and de-noising [11] - [13] .
After decomposition of each intrinsic mode function (IMF) meet the following two conditions:
1) Throughout the time sequence, the number of passing zero is equal to the number of the pole or at best, a difference;
2) At any point, the mean value composed of local maximum value upper envelope and lower local minima envelope must be zero.
2.2. The Basic Steps of EMD Decomposition
1) Find 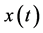 on all the maximum and minimum points, respectively, on the cubic spline interpolation to get the upper envelope
on all the maximum and minimum points, respectively, on the cubic spline interpolation to get the upper envelope  and lower envelope
and lower envelope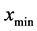 . The mean value of envelope is defined as
. The mean value of envelope is defined as 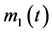
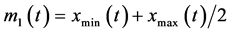 (1)
(1)
Using the original data after subtracting the mean can obtain:
 (2)
(2)
2) To determine whether 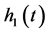 to meet the two conditions, if meet the
to meet the two conditions, if meet the 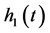 is the first order of the IMF, otherwise the
is the first order of the IMF, otherwise the 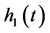 as a new signal repeat the above steps, so
as a new signal repeat the above steps, so
 (3)
(3)
Repeat the above process 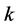 times, when the variance between
times, when the variance between 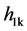 and
and 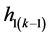 is satisfied the termination condition, such a
is satisfied the termination condition, such a 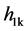 for the IMF, namely
for the IMF, namely
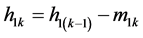 (4)
(4)
Assuming that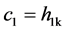 , define the remnants of the component for
, define the remnants of the component for



So you got the 




3. A De-Noising Method on EMD under Consecutive Mean Square Error Criterion
The thought of a de-noising method on EMD under consecutive mean square error criterion is [14] [15] , the first dealing with signal 


The concrete definition formula of consecutive mean square error criterion CMSE as shown below:

Among them, 

Namely find the global minimum position of the IMF as the cut-off point 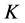
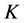


Collected at the scene of the track state detection, the sensor signals in the process of converted into digital signals, test circuit noise and the external environment, the influence of such factors as the observed acceleration signal in computer is mainly composed of periodic components, constant and noise. Therefore Formula (9) can be used to describe the acceleration signal:

In the formula,
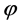



Using the EMD de-noising method under the rule of CMSE, to deal with the noise signal
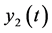
spectively, among them, 



is


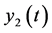
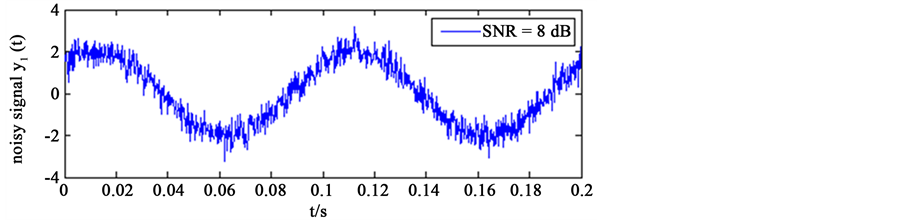

Figure 1. Different SNR of signal source

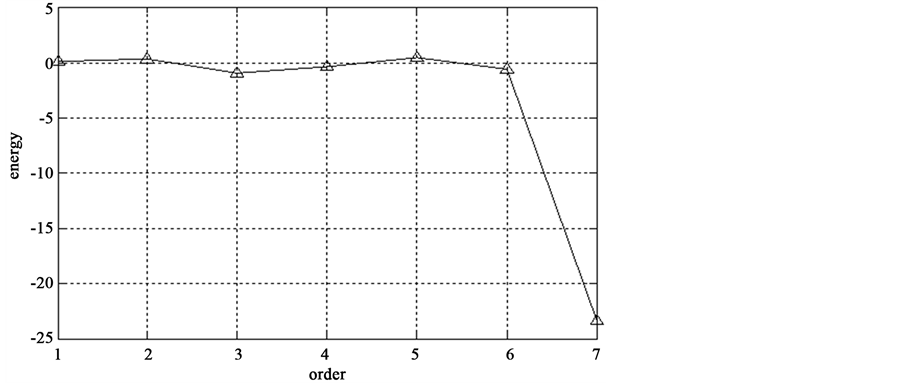
Figure 2. Energy change.


Figure 3. The de-noising results.
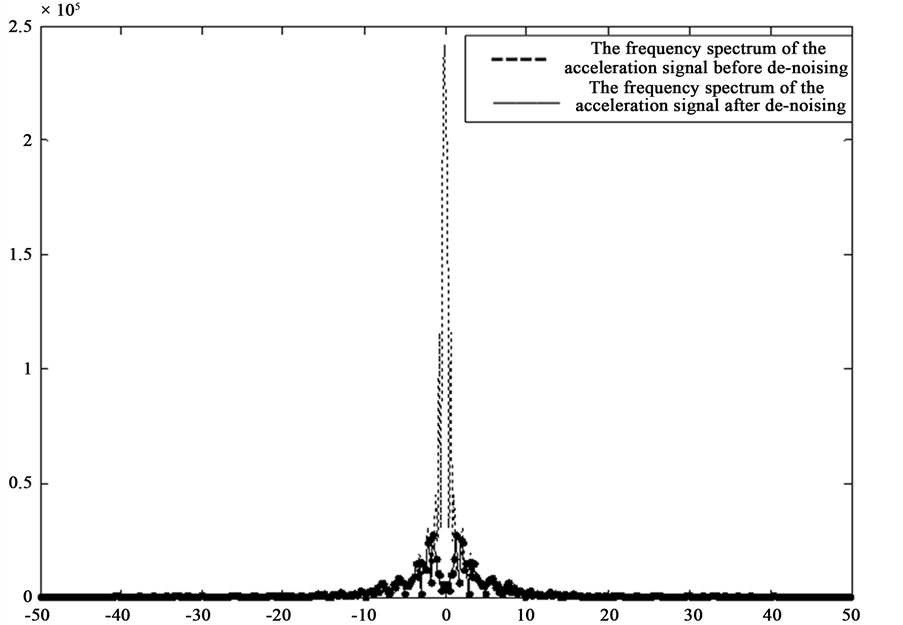
From Figure 3, the higher signal noise ratio (SNR), the de-noising effect is better; in low signal noise ratio (SNR), changed obviously after de-noising signal distortion. This shows that the de-noising method on EMD under consecutive mean square error criterion in the case of low signal noise ratio (SNR) de-noising performance is unstable [16] . The cause of this unstable basically has the following two points:
1) “One size fits all” approach only focus on who play a leading role in the IMF component, while ignoring the fact that useful signal in dominant mode of noise’s proportion is big, that remove noise but also remove the useful signal by mistake;
2) for any noise signal, the algorithm considered in the curves of the IMF's energy minimum weight must be a dominant mode noise of the IMF, however, under the condition of low signal noise ratio (SNR), the rule does not necessarily is founded.
Therefore, the Formula (7) for 
If the local minimum value exists before the global minimum, then
else,
4. The Analysis of Experiment Results
Experiment system uses XW-IMU5250 tiny mechanical inertial device of Beijing Star Neto Technology Development Co., Ltd., used as shown in Figure 4 shows the simulate rail cars as the carrier of strap down inertial system, in the process of experiment, to reduce the vector relative to the movement of the inertial measurement unit, inertial measurement unit should be installed in the center of gravity of the simulate rail cars, so as to improve the measurement accuracy of accelerometers.
In the experiments for loading of the inertial measurement unit testing the car through an analog line segments, and then collect the inertial measurement unit acceleration among the car movement. First of all, using the average filtering method to eliminate the acceleration signal contained in the direct current; Then this method is applied to the actual inertial unit signal noise processing.
With IMU5250 output 
Figure 4. The track on experimental platform.
Figure 5. IMF components of acceleration signal on y-axis after EMD decomposition.
From Figure 6 obtain the cut-off point 


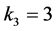

Figure 6. Acceleration energy changing curve on y-axis.
Figure 7. Comparison of y-axis acceleration spectrograms before and after the de-noising processing.
Figure 8. Spatial linear displacement.
5. Conclusion
This paper puts forward a kind of de-noising method for track state detection signal based on EMD under the CMSE principles, at the same time fixed the judgment methods of cut-off point
Acknowledgements
The project is jointly supported by the Shanghai Tertiary Education Speicalized Fund for Planning to Support Young Teacher’s Trainnings (ZZGJD12007), the Natural Science Foundation of Shanghai (12ZR1412300), the Science and Technology Commission of Shanghai Municipality Key Support Project (13510501300), and the Shanghai Graduate Education Innovation Project in Layout and Construction Project (13sc002).
References
- Zheng, S.B., Lin, J.H. and Lin, G.B. (2007) Maglev Track Long-Wave Irregularity Detection Based on Inertia Method and Its Implementation. Journal of Electronic Measurement and Instrument, 21, 61-65.
- Zheng, S.B., Lin, J.H. and Lin, G.B. (2007) High-Speed Maglev Track Long-Wave Irregularity Detection System Design. Chinese Journal of Scientific Instrument, 28, 1781-1786.
- Du, H.T. (2000) Long Wavelength Track Irregularity Detection Method of Digital Filter. China Railway Science, 4, 58-64.
- Zhu, H.T., Cai, J. and Wang, Z.Y. (2007) Based on the Orbit of Fiber Optic Gyroscope Direction Irregularity Detection System. Microcomputer Information, 23, 268-269.
- Boudraa, A.O. and Cexus, E.-C. (2007) EMD-Based Signal Filtering. IEEE Transactions on Instrumentation and Mea- surement, 56, 2196-2202. http://dx.doi.org/10.1109/TIM.2007.907967
- Tan, S.W., Qin, S.R. and Tang, B.P. (2004) The Hilbert-Huang Transform Filtering Properties and Application. Journal of Chongqing University, 27, 9-14.
- Zhao, W.W. and Zeng, X.W. (2008) A New Method of EMD De-Noising. Electronic Science and Technology, 5, 30- 32, 36.
- Zhu, W.F., Chai, X.D. and Zheng, S.B. (2012) Based on the Integration Filter Displacement Information Acquisition. Instrument Technique and Sensor, 11, 87-90.
- Ren, C.H., Xiong, L.X. and Zhao, X.J. (2010) Wavelet Threshold Filtering in Signal Processing, the Application of Fiber Optic Gyroscope. Piezoelectrics & Acoustooptics, 32, 957-959.
- Wang, T. (2010) The EMD Algorithm and Its Application in Signal Denoising. Haerbin Engineering University, Haerbin.
- Liu, L.J., Shen, Y. and Wang, Y. (2012) Radar Signal Filter Design Base on HHT Method. Control Conference (CCC), 3611-3616.
- Antonino-Daviu, J., Roger-Folch, J., Pons-Llinares, J., Pineda-Sanchez, M., Perez, R.B. and Charlton-Perez, C. (2011) Application of the Empirical Mode Decomposition to Condition Monitoring of Damper Bars in Synchronous Motors. Industrial Electronics (ISIE), Gdansk, 27-30 June 2011, 2118-2123.
- Yang, G.L., Zhu, Y.Q. and Yu, H.Y. (2010) The Automatic Seismic Signal Denoising Algorithm Based on HHT. Journal of Geodesy and Geodynamics, 3, 39-42.
- Zhu, L.P., Liu, A.J. and Wang, H.X. (2011) Based on the Radar Clutter Suppression of HHT. Modern Defense Technology, 6, 185-190.
- Gao, Y.C., Sang, E.F. and Liu, B.F. (2007) The Adaptive De-Noising Algorithm Based on Empirical Mode Decomposition. Computer Engineering and Applications, 43, 59-61.
- Sun, W.F., Peng, Y.H. and Xu, J.H. (2008) The Laser Noise Signal De-Noising Method Based on EMD. Journal of Shandong University, 38, 121-125.