Agricultural Sciences
Vol.06 No.05(2015), Article ID:56630,9 pages
10.4236/as.2015.65047
Illusion of a Density-Dependent Effect in Biology
Kazumi Sakuramoto
Department of Ocean Science and Technology, Tokyo University of Marine Science and Technology, Minato, Tokyo, Japan
Email: sakurak@kaiyodai.ac.jp
Copyright © 2015 by author and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 27 March 2015; accepted 19 May 2015; published 25 May 2015
ABSTRACT
Population changes are believed to be controlled by multiple factors, including an important density-dependent effect. This paper reviews the literature on this topic and shows that this density- dependent effect does not exist. This paper also gives a typical example in which no density-de- pendent effect was detected in the stock-recruitment relationship in Japanese sardines. The recruitment was found to be determined in proportion to the spawning stock biomass and to be affected by environmental factors. This simple mechanism is applicable not only in fish species but also in insects such as Thrips imaginis in Australia. The reason that many biologists have not become aware that the density-dependent effect does not exist is discussed using a metaphor. This paper proposes a new concept in the study of population change. The new concept proposed here will replace the currently used basic concept that has been assumed to be correct for more than 50 years.
Keywords:
Arctic Oscillation Index, Density-Dependent Effect, Ricker Model, Sardine, Stock-Recruitment Relationship

1. Introduction
The existence of a density-dependent effect is assumed as a matter of course, and doubts about this mechanism are typically not entertained. This consensus grew from a debate between scientists whose ideas differed drastically [1] -[7] . Davidson and Andrewartha [1] [2] found that the population size of Thrips imaginis can be predicted accurately based on temperature and precipitation data, and they concluded that the population size could be explained by the succession of good and bad seasons and by the heterogeneity of the places where they live [8] . However, Smith [5] reanalyzed the same data used by Davidson and Andrewartha [1] [2] and detected a density-dependent effect in the relationship between population change and population density. The result derived by Smith [5] greatly overshadowed the findings of Davidson and Andrewartha [1] [2] , and thereafter almost all biologists assumed the existence of a density-dependent effect. This effect has been widely considered an important factor in controlling population fluctuations.
Recently, however, Sakuramoto [9] reanalyzed Davidson and Andrewartha’s data [1] [2] and showed that the density-dependent effect found by Smith [5] was not valid. Sakuramoto [9] showed that the decreasing trend observed in the plot of population change against population size (density) did not imply the existence of a density-dependent effect. Such decreasing trends are always detected in response to observation errors contained in the dependent and/or independent variables. The results of the Monte-Carlo simulations conducted by Sakuramoto [9] also showed that the probability indicating a statistically significant false negative slope was high when the variance of the errors was high and/or the amount of data was large. Similar points have been made by Maelzer [10] , Kuno [11] and Ito [12] . They noted that in the attempts to detect a density-dependent effect using regression analysis, the error consistently acts as if it were a density-dependent effect. Under the effect of sampling error, the slope b for the regression of log Nt+1 on log Nt, for example, is expected to become <1 even where there is no density-dependent factor at all; note that Nt denotes the population in year t. Therefore, the results proposed by Sakuramoto [9] strongly indicated that the conclusion of Smith [5] was invalid and that no density-dependent effect existed in the population change in T. imaginis as Smith [5] asserted.
In the field of fisheries science, Sakuramoto and Suzuki [13] conducted detailed simulations to confirm whether or not a density-dependent effect truly exists in the stock-recruitment relationship. The stock-recruit- ment relationship shows a relationship between spawning stock biomass (SSB) and recruitment (R) that has been a main issue in fisheries population dynamics. They showed the mechanism by which the density-dependent effect was erroneously detected in response to observed and/or process errors in the variables. In particular, the density-dependent effect was large when the errors in the independent variables increased. Further, Sakuramoto and Suzuki [13] specifically proposed that the opposite result was not possible. That is, when the true model showed a density-dependent effect, as in the Ricker [14] or Beverton and Holt model [15] , the proportional model was seldom selected in response to process and/or observation errors. This suggests that if a proportional model is identified to analyze actual data, in almost all cases, the proportional model is not erroneously produced in response to process and/or observation errors.
2. Material and Methods
2.1. Data
This paper used the spawning stock biomass (SSB) and recruitment (R) data for the Pacific stock of Japanese sardines. The data from 1951 to 1975 were obtained from Yatsu et al. [16] and those from 1976 to 2012 were obtained from Kawabata et al. [17] . The index of Arctic Oscillation was obtained from the NOAA Climate Prediction Center [18] .
2.2. Model and Statistical Methods
I discuss the stock-recruitment relationship, which refers to the relationship between spawning stock biomass and recruitment and is considered a key issue in fisheries sciences. It is usually plotted in the form of ln(R) against ln(SSB). That is,
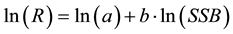 (1)
(1)
If no density-dependent effect exists, the slope of the regression line, b, is equal to unity; however, if a density-dependent effect exists, b is less than unity. Usually we ignore the case when the slope is greater than unity, although it also signifies the existence of a density-dependent effect; however, it is a special case of the density-dependent effect and seldom occurs.
In this study, I used three regression methods to plot ln(R) against ln(SSB), i.e., simple regression analysis, Deming regression analysis [19] , and Passing and Bablok regression analysis [20] . A simple regression analysis is problematic in that it assumes that there is no observation error in the independent variable; therefore, parameter estimates derived from a simple regression analysis exhibit bias [10] -[12] . When both independent and dependent variables contain observational errors, the Deming and Passing and Bablok regression analyses can effectively remove the bias inherent in a simple regression analysis. The estimations using the Deming and Passing and Bablok regression analyses were conducted using the programs developed by Aoki [21] [22] .
3. Results
3.1. Why Have Biologists Not Noticed This Mistake?
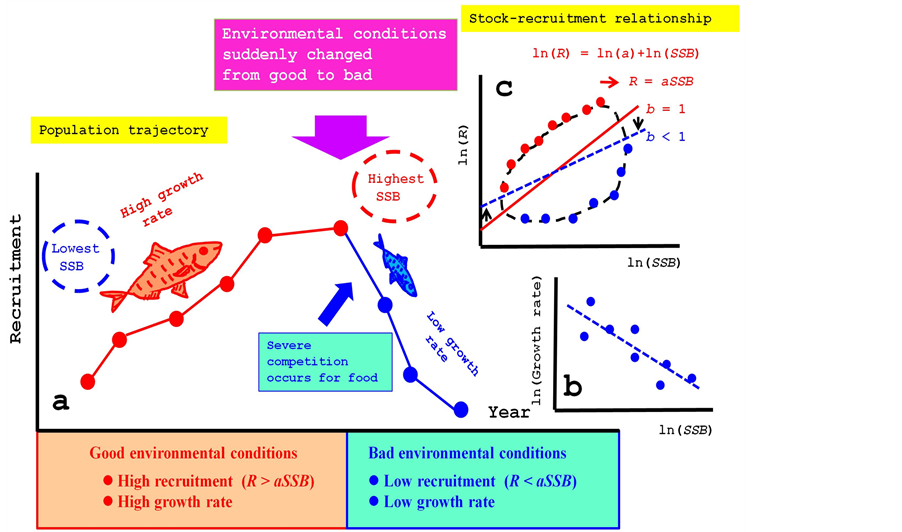
As I mentioned above, many papers have pointed out that false density-dependent effects were detected by the regression lines even where there was no density-dependent factor at all [9] -[13] . Still, up to the present, many biologists discuss the existence of density-dependent effects using regression analysis and still assume the existence of density-dependent effects [6] [7] [16] [23] -[26] . Apparently they are influenced by seemingly clear evidence indicating the existence of density-dependent effects. For instance, it has been found that body size or body weight decreases when the density is high [19] [26] . However, such phenomena do not indicate the existence of a density-dependent effect any more than a regression line with a slope less than unity indicates the existence of a density-dependent effect. Using the metaphor shown in Figure 1, I will try to explain why biologists have continued to assume the existence of a density-dependent effect.
Figure 1 shows three components that determine the stock-recruitment relationship. Two components, R and SSB, have a biological relationship that is proportional: R = a∙SSB. The third component is environmental conditions, which are represented in the figure by the sun. Environmental conditions strongly affect R and SSB, and as a result, two shadows are constructed, which change depending on the position of the sun (i.e., the environmental conditions). Usually, some observation errors (eε, eλ) are present when these shadows of R and SSB are observed, (Robs, SSBobs), as the components R and SSB themselves cannot be observed directly. Figure 1 metaphorically shows these differences using the relationship between the sun and the shadows.
Figure 1. Three components that determine the stock-recruitment relationship. Two components, R and SSB, have a biological relationship that is proportional: R = a∙SSB. The third component is environmental conditions, which are represented in the figure by the sun. Environmental conditions strongly affect R and SSB, and as a result, two shadows are constructed, which change depending on the position of the sun (i.e., the environmental conditions). Usually, some observation errors (eε, eλ) are present when these shadows of R and SSB are observed, (Robs, SSBobs), as the components R and SSB themselves cannot be observed directly.
The current model of the stock-recruitment relationship simply treats the two-dimensional relationship between Robs and SSBobs, which can be referred to as a “closed model”, which treats only intra-specific relationships such as the relationship between variables within a species. It does not consider other variables outside of the intra-specific relationship. Figure 1 clearly shows that this approach is wrong, because Robs and SSBobs are not the observed values of the components R and SSB, but the observed values of the shadows of components R and SSB. Therefore, not wo-dimensional model for Robs and SSBobs can express the direct biological relationship between the components R and SSB. Three or more than three-dimensional open model could express the relationship between Robs and SSBobs. An “open model” incorporates variables related not only to the biological inter-specific relationship but also to physical environmental factors.
Therefore, if a density-dependent effect is detected in the relationship between these two shadows (Robs and SSBobs), this only indicates that a density-dependent effect exists in the relationship between the two shadows, not in the relationship between the components R and SSB. That is, we have so far discussed the stock-recruit- ment relationship using those two shadows, Robs and SSBobs, not R and SSB.
Here I explain using time series data why biologists have come to unconsciously believe in the existence of a density-dependent effect (Figure 2). When the environmental conditions are good for a species, for instance, the temperature is suitable for the species and the abundance of prey is high. Under good environmental conditions, the recruitment and the body size growth rate of fish are higher than those determined under regular environmental conditions. As a result, SSB also increases in response to the high recruitment. When those good conditions continue for several years, the SSB will continuously increase at an extremely high level. However, those good conditions will not continue forever. An abrupt large change from good to bad conditions is likely to occur at some point. The temperature will no longer be suitable for the species, and the abundance of prey will decrease. Then, strong reductions in the survival and growth rates will occur because of the bad environmental conditions. Not only a reduction in recruitment but also reductions in the weight and body size of the fish simultaneously occur at high SSB levels.
Figure 2. Why do biologists misunderstand the density-dependent effect? Recruitment, R, is significantly influenced by environmental conditions. When environmental conditions are good, R increases, and vice versa. When environmental conditions change from good to bad, severe competition for food occurs and body size decreases (a). Then, an apparent density-dependent effect between SSB and body size is observed (b). Along with the cyclic pattern of environmental conditions, R and SSB also show similar cyclic patterns. Then, these two cyclic patterns produce a loop in the stock-recruitment relationship (c).
Therefore, when we investigate the relationship between body size and SSB, or recruitment and SSB, clear density-dependent relationships between them will seem to exist. However, there is no direct relationship between body size and SSB or recruitment and SSB. Changes in body size, recruitment, and SSB all originally occurred in response to environmental factors. That is, the environmental change, not the high SSB density, produces the reductions in both body size and recruitment.
3.2. A New Proposed Mechanism for Population Changes
Using the stock-recruitment data for Japanese sardines [16] [17] and Arctic Oscillation (AO) data [18] , I here propose a surprisingly simple mechanism that can explain the population fluctuations.
Figure 3 shows the plot of ln(Rt) versus ln(SSBt) for Japanese sardines. The slope estimated by a simple regression analysis, shown by a thin line, was 0.769, and the 95% confidence interval was (0.585, 0.953). That is, the estimated slope was statistically less than unity, and a density-dependent effect was detected. However, Maelzer [10] , Kuno [11] and Ito [12] pointed out that the slope b for the regression line becomes less than unity even where there is no density-dependent factor at all. When the Deming regression [19] [21] and Passing- Bablok regression [20] [22] , which are regression analyses applicable to cases in which errors also exist in the independent variables, were applied, the estimated slopes (95% confidence intervals) were 0.899 (0.794, 0.969) and 0.979 (0.900, 1.075), respectively. In the Deming regression, the slope was larger than that estimated by a simple regression analysis; however, the upper limit of the 95% confidence interval was slightly less than unity. When the Passing-Bablok regression was applied, the slope was not statistically different from unity. A detailed discussion was given in Sakuramoto [27] . The regression line estimated by the Passing-Bablok regression is shown as a thick line in Figure 3. Hereafter, I use the regression line estimated by the Passing-Bablok regression method as the line that expresses the stock-recruitment relationship of Japanese sardines. That is:
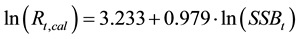 (2)
(2)
Figure 3. Stock recruitment relationship observed in Japanese sardine. The thin and thick lines denote the regression lines estimated by simple and Passing and Bablok regression analyses. Three loops, plotted by purple, blue and green closed circles, were recognized regardless of the stock levels. Numbers indicate years.
Figure 3 shows that when the observed recruitment in year t, ln(Rt,obs), was higher than that on the line shown in Equation (1), SSBt+2 increased, and vice versa, regardless of the ln(SSBt) level. For instance, ln(SSBt) was extremely low, around 2 to 4, in some years such as 1969, 1970 and 1971, the values of ln(Rt,obs) were much higher than those on the line, and in some years, such as 1961-1966, they were much lower than those on the line. The situation was the same in cases in which the ln(SSBt) level was extremely high, around 6 to 9. Table 1 shows the values of ln(Rt,obs) − ln(Rt,cal) and ln(SSBt+2) − ln(SSBt). The number of years that satisfied both ln(Rt,obs) > ln(Rt,cal) and ln(SSBt+2) > ln(SSBt) was 27 (shown in blue closed circles), and the number that satisfied both ln(Rt,obs) < ln(Rt,cal) and ln(SSBt+2) < ln(SSBt) was 22 (shown in red closed circles). Therefore, in 49 out of 60 years (more than 82%), the increase or decrease in SSB was simply determined by whether recruitments were above or below the regression line shown in Equation (1), regardless of the levels of recruitment and SSB. This indicates that the population fluctuation mechanism is surprisingly simple. The value of ln(SSBt+2) increases when ln(Rt,obs) > ln(Rt,cal) and decreases when ln(Rt,obs) < ln(Rt,cal) regardless of the ln(SSBt) level. These findings never indicate the existence of a density-dependent effect, such as recruitment showing a supplementary increase when ln(SSBt) is low or tending to decrease in response to a high ln(SSBt) value.
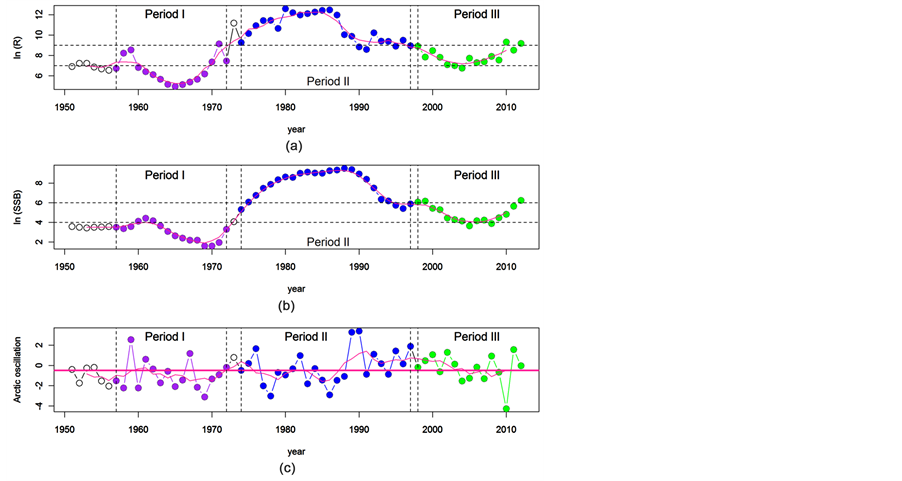
Figure 3 further shows three loops surrounding the regression line for three levels of SSB. One loop was formulated for low ln(SSBt) values around 2 to 4, which correspond to the years from 1957 to 1972 (we will call these years Period I). The second loop was formulated for high SSB values in the years from 1974 to around 1997 (Period II). The third loop was a narrow loop formulated along the line and corresponding to the years from 1998 to 2012 (Period III). In each period, the trajectories of ln(R) and ln(SSB) showed cyclic patterns, although the levels of ln(SSB) and ln(R) were all different (Figures 4(a)-(b)). The cyclic patterns of ln(R) coincided with the levels of AO in February (Figure 4(c)). In the years when AO was greater than the average of −0.437 (horizontal line), recruitment showed a decreasing trend, and vice versa. Therefore, it seems that the increasing or decreasing trend of the recruitment had the same strong relationship with the value of AO in February.
When the recruitment was above the regression line shown in Equation (1), the SSB related to the recruitment began to increase, and the trajectory on the R-SSB plane was increasing and concave. In contrast, when recruitment was below the line, the SSB began to decrease, and the trajectory on the R-SSB plane was decreasing and convex. Therefore, two cyclic patterns in ln(R) and ln(SSB) generate a loop shape shown in Figure 2(c) and noted by Sakuramoto [28] . This is the mechanism by which the loop is produced and why it always appears in the stock-recruitment relationship.
4. Discussion
Sakuramoto [9] [29] simply summarized the general stock-recruitment model as follows:
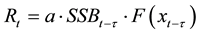 (3)
(3)
where τ denotes the time lag that corresponds to the age of recruitment. For Japanese sardines, τ = 0, because recruitment occurs at age 0. Then, Rt denotes the recruitment in March-May of year t, SSBt denotes the spawning stock biomass in January of year t, and f(.) denotes a function that determines the effects of environmental conditions in year t, xt = [xt,1, …, xt,k] (k denotes the number of environmental factors). For Japanese sardines, the Kuroshio Extension sea surface temperature in February of year t and the AO in February of year t were used as the environmental conditions. In particular, the crucial failures in recruitment that occurred from 1988 to 1991 can be explained by huge changes in environmental factors such as AO and sea surface temperature in the sou- thern area of the Kuroshio Extension during the spawning season [30] .
The letter a indicates a proportional constant. That is, the population fluctuation mechanism is surprisingly simple.
As shown in Figure 3, in the case of Japanese sardines, three loops appeared, one at each stock level. These are usually observed. For instance, the anchoveta stock-recruitment relationship in Peru also showed two loops, one each on the high and low SSB levels [31] . Other examples in which the stock-recruitment relationship showed loops were reported by Walters [32] and Zhen and Kruse [33] . Walters [32] showed the relationship between surplus production and stock size in the case of the Northeast Atlantic herring stocks. He noted that three of the stocks (North Sea, Norwegian Spring and Celtic) represented one-way trips, and two stocks (west of Scotland and Iceland spring spawners) showed a loop pattern, which has a clockwise direction. Sakuramoto [28]
Table 1. Surplus recruitments (R) produced by environmental factors increase SSB. ln(Rt,cal) denotes the recruitment calculated by the equation: ln(Rt,cal) = 3.233 + 0.979 ln(SSBt). ln(Rt,obs) and ln(SSBt) denote the observed recruitment and SSB in year t, respectively. The years satisfied both ln(Rt,obs) > ln(Rt,cal) and ln(SSBt+2) > ln(SSBt) are marked by blue closed circles. The years that satisfied both ln(Rt,obs) < ln(Rt,cal) and ln(SSBt+2) < ln(SSBt) are marked by red closed circles.
Figure 4. Trajectories of ln(R), ln(SSB) and the index of Arctic Oscillation (AO) in February. The purple curves in each panel indicate five-year moving averages. The three periods marked by different color correspond to the three loops shown in Figure 3. The horizontal thick line in panel c denotes the mean value of AO, which is −0.473.
showed that the Pacific stock of mackerel (Scomber japonicus) in Japan, the stock of saury (Cololabis saira) in the Pacific Ocean off of northern Japan, pink salmon (Onchorhynchus gorbuscha) at McClinton Creek, BC, Canada, Pacific herring (Clupea pallasii), and North Sea haddock (Melanogrammus aeglefinus) also showed the loop shapes.
When environmental conditions change from good to bad, the per capita amount of food decreases in proportion to the population size. Some may insist that this phenomenon is a “density-dependent effect”. However, it always occurs regardless of the density. Figure 3 shows that bad conditions occurred at three SSB levels, low (around 3.6), middle (around 6.0) and high (around 9.3). This indicates that a “density-dependent effect” occurred regardless of the density. Figure 3 shows the case when the number of years was 60. If the number of years was, for instance, 600, around 30 circles would have emerged. That is, when the per capita amount of food decreases, reductions in recruitment from high to low would occur at around 30 different SSB values. This means that a “density-dependent effect” occurs regardless of the density; in other words, this phenomenon is not a density-dependent effect.
As shown in this paper, the population fluctuation mechanism is surprisingly simple. The recruitment, Rt, is determined in proportion to SSBt, and further, the recruitment is affected by environmental factors. That is, when ln(Rt,obs) > ln(Rt,cal), SSBt+2 increases, and when ln (Rt,obs) < ln(Rt,cal), SSBt+2 decreases. The difference between ln(Rt,obs) and ln(Rt,cal) occurs in response to environmental factors. This is the mechanism by which populations fluctuate. Of course, fishing also affects the survival process, and this was discussed in detail in Sakuramoto [29] and Sakuramoto et al. [34] .
This paper proposes a new concept in the study of population change. The new concept proposed here will replace the currently used basic concept that has been assumed to be correct for more than 50 years.
Acknowledgements
I thank Drs. Seizo Hasegawa and Mitsuo Sakai for his useful comments that improved this manuscript.
References
- Davidson, J. and Andrewartha, H.G. (1948) Annual Trends in a Natural Population of Trips Imagines (Thysanoptera). Journal of Animal Ecology, 17, 193-199. http://dx.doi.org/10.2307/1484
- Davidson, J. and Andrewartha, H.G. (1948) The Influence of Rainfall, Evaporation and Atmospheric Temperature on Fluctuations in the Size of a Natural Population of Thrips imaginis (Thysanoptera). Journal of Animal Ecology, 17, 200-222. http://dx.doi.org/10.2307/1485
- Nicholson, A.J. and Bailey, V.A. (1935) The Balance of Animal Populations. Part I. Proceedings of the Zoological Society of London, 105, 551-598. http://dx.doi.org/10.1111/j.1096-3642.1935.tb01680.x
- Huffaker, C.B. (1958) The Concept of Balance in Nature. Proceeding Tenth Internet. Congress of Entomology, 2, 625- 636.
- Smith, F.E. (1961) Density Dependence in the Australian Thrips. Ecological Society of America, 42, 403-407. http://dx.doi.org/10.2307/1932093
- Sibly, R.M., Barker, D., Denham, M.C., Hone, J. and Pagel, M. (2005) On the Regulation of Populations of Mammals, Birds, Fish, and Insects. Science, 22, 607-610. http://dx.doi.org/10.1126/science.1110760
- Brook, B.W. and Bradshaw, C.J.A. (2006) Strength of Evidence for Density Dependence in Abundance Time Series of 1198 Species. Ecology, 87, 1445-1451. http://dx.doi.org/10.1890/0012-9658(2006)87[1445:SOEFDD]2.0.CO;2
- Birch, L.C. and Browning, T.O. (1995) Herbert George Andrewartha 1907-1992. Australian Academic of Society. http://www.sciencearchive.org.au/fellows/memoirs/andrewartha.html
- Sakuramoto, K. (2014) A Common Concept of Population Dynamics Applicable to Both Thrips Imaginis (Thysanoptera) and the Pacific Stock of the Japanese Sardine (Sardinops melanostictus). Fisheries and Aquaculture Journal, 4, 140-151.
- Maelezer, D.A. (1970) The Regression of log Ni+1 on log Ni as a Test of Density Dependence: An Exercise with Computer-Constructed Density-Dependent Populations. Ecology, 51, 810-822. http://dx.doi.org/10.2307/1933973
- Kuno, E. (1971) Sampling Error as a Misleading Artifact in “Key Factor Analysis”. Research Population Ecology, 13, 28-45. http://dx.doi.org/10.1007/BF02522011
- Ito, Y. (1972) On the Methods for Determining Density-Dependence by Mean of Regression. Oecologia, 10, 347-372. http://dx.doi.org/10.1007/BF00345737
- Sakuramoto, K. and Suzuki, N. (2012) Effect of Process and/or Observation Errors on the Stock-Recruitment Curve and the Validity of the Proportional Model as a Stock-Recruitment Relationship. Fisheries Science, 78, 41-45. http://dx.doi.org/10.1007/s12562-011-0438-4
- Ricker, W.E. (1954) Stock and Recruitment. Journal of the Fisheries Research Board of Canada, 11, 559-623. http://dx.doi.org/10.1139/f54-039
- Beverton, R.J.H. and Holt, S.J. (1957) On the Dynamics of Exploited Fish Populations. Fishery Investigations Series II 19 [1-533], Her Majesty’s Stationery Office, London.
- Yatsu, A., Watanabe, T., Ishida, M., Sugisaki, H. and Jacobson, L.D. (2005) Environmental Effects on Recruitment and Productivity of Japanese Sardine Sardinops melanostictus and Chub Mackerel Scomber japonicus with Recommendations for Management. Fisheries Oceanography, 14, 263-278. http://dx.doi.org/10.1111/j.1365-2419.2005.00335.x
- Kawabata, J., Honda, S., Watanabe, C., Okamura, H. and Ichinokawa, M. (2014) Stock Assessment and Evaluation for the Pacific Stock of Japanese Sardine (Fiscal Year 2013). In: Marine Stock Fisheries Stock Assessment and Evaluation for Japanese Waters (Fiscal Year 2013/2014), Fisheries Agency and Fisheries Research Agency, Japan, 15-46.
- AO, Arctic Oscillation NOAA Climate Prediction Center (2014) Web: http://www.cpc.ncep.noaa.gov/products/precip/CWlink/daily_ao_index/monthly.ao.index.b50.current.ascii.table
- Deming, W.E. (1943) Statistical Adjustment of Data [1-261]. Dover Publication Inc., New York.
- Passing, H. and Bablok, W. (1983) New Biometrical Procedure for Testing the Equality of Measurements from Two Different Analytical Methods. Application of Linear Regression Procedures for Method Comparison Studies in Clinical Chemistry, Part I. Journal of Clinical Chemistry& Clinical Biochemistry, 21, 709-720. http://dx.doi.org/10.1515/cclm.1983.21.11.709
- Aoki, S. (2009) Parameter of a Regression Line Estimated by Deming Regression Method. http://aoki2.si.gunma-u.ac.jp/R/Deming.html
- Aoki, S. (2009) Parameter of a Regression Line Estimated by Passing Bablok Regression Method. http://aoki2.si.gunma-u.ac.jp/R/PassingBablok.html
- Ohman, M.D. (2001) Density-Dependent Mortality in an Ocean Copepod Population. Nature, 412, 638-641. http://dx.doi.org/10.1038/35088068
- Mayers, R.A. (2001) Stock and Recruitment: Generalizations about Maximum Reproductive Rate, Density Dependence, and Variability Using Meta-Analytic Approaches. ICES Journal of Marine Science, 58, 937-951. http://dx.doi.org/10.1006/jmsc.2001.1109
- Imre, I., Grant, J.W.A. and Cunjak, R.A. (2005) Density-Dependent Growth of Young-of-the-Year Atlantic Salmon Salmo salar in Catamaran Brook New Brunswick. Journal of Animal Ecology, 74, 508-516. http://dx.doi.org/10.1111/j.1365-2656.2005.00949.x
- Sundstrom, L.F., Kaspersson, R., Naslund, J. and Johnsson, J.I. (2013) Density-Dependent Compensatory Growth in Brawn Trout (Salmo trutta) in Nature. PloS ONE, 8, 1-7. http://dx.doi.org/10.1371/journal.pone.0063287
- Sakuramoto, K. (2012) A New Concept of the Stock-Recruitment Relationship for the Japanese Sardine, Sardinops melanostictus. The Open Fisheries Science Journal, 5, 60-69.
- Sakuramoto, K. (2005) Does the Ricker or Beverton and Holt Type of Stock-Recruitment Relationship Truly Exist? Fisheries Sciences, 71, 577-592. http://dx.doi.org/10.1111/j.1444-2906.2005.01002.x
- Sakuramoto, K. (2013) A Recruitment Forecasting Model for the Pacific Stock of the Japanese Sardine (Sardinops Melanostictus) That Does Not Assume Density-Dependent Effects. Agricultural Science, 4, 1-8. http://dx.doi.org/10.4236/as.2013.46A001
- Sakuramoto, K., Shimoyama, S. and Suzuki, N. (2010) Relationships between Environmental Conditions and Fluctuations in the Recruitment of Japanese Sardine Sardinops melanostictus in the Northwestern Pacific. Bulletin of Japanese Society of Fisheries and Oceanography, 74, 88-97.
- Singh, A.A., Sakuramoto, K. and Suzuki, N. (2014) Model for Stock-Recruitment Dynamics of the Peruvian Anchoveta (Eugraulis ringens) off Peru. Agricultural Sciences, 5, 140-151. http://dx.doi.org/10.4236/as.2014.52017
- Watlers, C.J. (1987) Nonstationarity of Population Relationships in Exploited Populations. Canadian Journal of Fishers and Aquatic Sciences, 44, 156-165. http://dx.doi.org/10.1139/f87-319
- Zheng, J. and Kruse, G.H. (2003) Stock-Recruitment Relationships for Three Major Alaskan Crab Stocks. Fisheries Research, 65, 103-121. http://dx.doi.org/10.1016/j.fishres.2003.09.010
- Sakuramoto, K., Sugiyama, H. and Suzuki, N. (2001) Models for Forecasting Sandfish Catch in the Coastal Waters off Akita Prefecture and the Evaluation of the Effect of a 3-Year Fisheries Closure. Fisheries Sciences, 67, 203-213. http://dx.doi.org/10.1046/j.1444-2906.2001.00241.x