Journal of Data Analysis and Information Processing
Vol.04 No.02(2016), Article ID:66577,17 pages
10.4236/jdaip.2016.42006
Robust Regression Analysis with LR-Type Fuzzy Input Variables and Fuzzy Output Variable
Dan Zhang, Qiujun Lu
College of Science, University of Shanghai for Science and Technology, Shanghai, China

Copyright © 2016 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 11 January 2016; accepted 15 May 2016; published 19 May 2016
ABSTRACT
In this paper, we propose a fuzzy linear regression model with LR-type fuzzy input variables and fuzzy output variable, the fuzzy extent of which may be different. Then we give the iterative solution of the proposed model based on the Weighted Least Squares estimation procedure. Some properties of the estimates are proved. We also define suitable goodness of fit index and its adjusted version useful to evaluate the performances of the proposed model. Based on the Least Median Squares-Weighted Least Squares (LMS-WLS) estimation procedure, we give robust estimation steps for the proposed model. Compared with the well-known fuzzy Least Squares method, the effectiveness of our model on reducing the outliers influence is shown by using two examples.
Keywords:
LR-Type Fuzzy Input Variables, LR-Type Fuzzy Output Variable, LMS-WLS, Outliers, Robust

1. Introduction
Fuzzy linear regression analysis is a well-known method for seeking the fuzzy relationship between inputs and output data. Fuzzy linear regression is useful in a fuzzy domain where model parameters and/or data are fuzzy, or imprecise, or vague. The main approaches of fuzzy linear regression are Possibilistic concepts introduced by Tanaka et al. [1] and Least-Squares (LS) approach that extends the LS criterion to fuzzy setting [2] . The probabilistic approaches mainly involve a linear mathematical programming method and their aim is to cover the spreads of the output up to an h-level [3] . On the other hand, in the least squares, the objective is to maximize the model fitting measure between the estimated outputs from the estimated model and the observed outputs. For contributions on this subject see Refs. [2] [4] - [10] . The LS method has several theoretical and applicative advantages, but it has a critical drawback, because it is extremely sensitive to the presence of outliers. In the fuzzy regression literature, the outlier problem has been solved with regard to both outlier detection criteria and robust estimation procedures. In the following, we briefly illustrate some contributions on robust estimation procedures.
Watada and Yabuuchi [11] propose a robust fuzzy regression model based on a hyperelliptic function. Chang and Lee [5] have suggested generalized fuzzy weighted least squares method for an outlier condition, making weighted with degree of membership and lean on an interaction with the decider. For a simple regression, Yang and Ko [12] suggest weighted fuzzy at the least squares of analyzed iterative algorithm, which has two stages. Oussalsh and Schutter [13] make use of Least Trimmed Squares (LTS) and Least Median Squares (LMS) for the fuzzy regression model, and study the performance of the proposed model when data is contaminated by outliers. Yang and Liu [14] have suggested the fuzzy least squares for models of fuzzy interaction linear regression. This algorithm is robust against the outlier for simple regression. Şanli and Apaydin [15] propose a robust estimation procedure for fuzzy linear regression model with fuzzy input-output based on the least median squares.
In recent years, there is a growing literature that is related to robust fuzzy regression in a fuzzy domain. Varga [16] presents two robust estimations of unknown fuzzy parameters in fuzzy regression model, and investigates the relationship between the proposed models both for fuzzy and non-fuzzy regression analysis. Choi and Buckley [17] utilize the Least Absolute Deviations (LAD) for the fuzzy regression model, and investigate the performance of the model when data contains fuzzy outliers. Kula and Apaydin [18] propose a robust fuzzy regression analysis based on the ranking of fuzzy sets. On the basis of Modarres et al. [19] [20] , a robust nonlinear fuzzy regression model using multilayered feedforward neural networks where weights, biases, input and output variables are assumed to be fuzzy is presented by Nasrabadi and Hashemi [21] . Hu [22] suggests a genetic-algo- rithm-based method for determining two functional-link nets for the robust nonlinear interval regression model. A robust version of a spline-based estimate is presented by Maronna and Yohai [23] , which has the form of an MM-estimate. D’Urso et al. [24] propose a robust fuzzy linear regression model with crisp inputs and fuzzy outputs based on the least median squares-weighted least squares estimation procedure. Based on the least trimmed squares estimation, Chachi and Roozbeh [25] propose a estimation procedure for determining the coefficients of the fuzzy regression model for crisp input-fuzzy output data (see also D’ Urso et al. (2011) for a list of possible references on the topic of robust fuzzy regression analysis).
The rest of the paper is organized as follows. In Section 2, we set up the fuzzy regression model for fuzzy input variables (explanatory variables or independent variables) and fuzzy output variable (dependent variable or response variable) according to Refs. [8] [9] . Then, in Section 3, the estimation procedure is described. This is based on the Weighted Least Squares (WLS) principle. WLS objective function is defined (Section 3.1). An iterative WLS solution is shown in section 3.2 and some relevant properties of this solution are proved in Section 3.3, while in section 3.4 special case of model is discussed. In Section 4, we introduce some goodness of fit indices to assess model fitting. In Section 5, by considering the Least Median Squares and the Weighted Least Squares (LMS-WLS) approach, we give steps of the LMS-WLS estimation procedure with fuzzy output variable and fuzzy input variables. Section 6 reports an example and a simulation study to illustrate the effectiveness of our model in presence of outlier. Finally, Section 7 contains concluded remarks.
2. The Linear Regression Model with LR-Type Fuzzy Input Variables and Output Variable
Let consider a fuzzy output variable Y and p fuzzy input variables 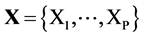 observed on n units. Data are denoted by
observed on n units. Data are denoted by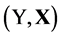 . We assume that Y is a LR-type fuzzy variable:
. We assume that Y is a LR-type fuzzy variable: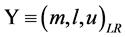 , where m is the center, l and u the left spread and right spread respectively;
, where m is the center, l and u the left spread and right spread respectively; 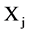 is also a LR-type fuzzy variable:
is also a LR-type fuzzy variable: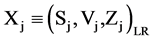 , where
, where 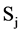 is the center,
is the center, 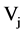 and
and  the left spread and right spread of the jth LR-type fuzzy input variable.
the left spread and right spread of the jth LR-type fuzzy input variable.
Let 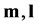 and
and 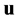 be the vectors of the observed centers, left spreads and right spreads, respectively. Firstly, we model the observed centers and lower and upper boundary of the response variable, as sums of unknown theoretical values and of their respective residuals:
be the vectors of the observed centers, left spreads and right spreads, respectively. Firstly, we model the observed centers and lower and upper boundary of the response variable, as sums of unknown theoretical values and of their respective residuals:
 (1)
(1)
where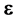 ,
,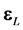 and
and 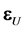 are the vectors of residuals and
are the vectors of residuals and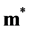 ,
, 


where








3. The Estimation Procedure
3.1. Distance and Objective Function
In some cases, it may happen that the membership functions of the dependent variable vary across the observation units. This can occur if we allow for different levels of uncertainty associated with each response: for instance, a person might be extremely sure about her/his opinion, but another one might be rather uncertain. These levels of uncertainty may then correspond to square root and parabolic membership functions, respectively. The very common triangular membership function can be seen as expressing a medium level of uncertainty. Based on the above consideration, according to the WLS criterion, once weights are determined, the parameters of the model (2) should be estimated by the minimizing the weighted squared distance between the observed values of the response variable Y, and the corresponding estimated values 

where the influence of the shape of the relationship function on the distance is embodied in the matrices 







On the basis of distance, we can set the WLS objective function in terms of the parameters 

3.2. Iterative Weighted Least Squares Solution
In order to solve minimize (4), we equate to zero the partial derivatives of 








An iterative solution of the above system can be based on the following set of equations, orderly derived from Equations (5)-(11).







3.3. Properties of the WLS Solution of the Proposed Model
In this section we will prove some propositions showing useful properties of the WLS solution illustrated in Section 3.2.
Proposition 1 
Proof By (7), (8) and (9), we have



Due to


Finally, by (20) and (21) into (23), we obtain
Proposition 2 
Proof Set
Merge (9), (10) and (11), we obtain that

Then, we have

By considering (5) and (6), we obtain


Finally, by substituting (27) and (28) into (26), we obtain
3.4. Special Case of the Model
In the symmetric case






The distance (3) turns into

Therefore we iterate the procedure described in section 3.2.We derive the following symmetric iterative weighted least squares solutions.








4. Goodness of Fit
In this section, in order to measure the goodness of fit for a multiple regression model with LR-type fuzzy output variable and fuzzy input variables, we define the coefficient of determination and its adjusted version.
Definition 1 For the LR-type fuzzy output variable
The total weighted deviation of fuzzy output variable, given by the weighted total sum of squares:

where




The weighted deviation “explained” from the model, given by the weighted regression sum of squares:

The residuals weighted deviation, i.e. the deviation not explained from the model, given by the weighted sum of squares of errors:

Propositions 3 The total weighted deviations of




Proof The expression concerning 


To prove the decomposition (43), we have to verify that the following term is null:

After a little algebra, we can write (44) as

which is null, taking into account the finding of proposition 1, proposition 2, (20) and (21).
Definitions 2 The goodness of fit index for the model (2) estimated by WLS is defined as follows:

Given the relationship between


From proposition 3 follows that



Definition 3 The adjusted coefficient of determination is defined as follows:

The adjusted 


5. Steps of the LMS-WLS Estimation Procedure
In this section, we illustrate the steps of the suggested robust estimation procedure based on the Least Median Squares-Weighted Least Squares (LMS-WLS) [24] , LMS is used to give the initial solution of WLS to ensure robustness of the model:
1. Given n observations on one LR-type fuzzy dependent variable and fuzzy independent variables, we randomly select a sub-sample of 
2. Regression parameters 

3. At the first step, the estimators 

And then to compute the squared residuals:
4. Finally, we compute the median of the estimated squared residuals:
Steps 1 - 4 are repeated until convergence is achieved. At the kth iteration, we obtain, the estimators 






In order to enhance these estimates, we employ the WLS procedure, assigning to each observation a weight. A simple way to weight observations on the basis of residuals [24] is:

where 

where



6. Numerical Experiment
In order to evaluate the proposed model, we show two examples. As for the WLS phase of the estimation procedure, weights (48) are assigned to data, putting
6.1. Example 1
In this example, we consider a fuzzy linear regression model, in which we consider fuzzy output data and fuzzy input data with a triangular fuzzy number, putting






where
On the sample of 8 units we have simulated a fuzzy output variable and a fuzzy input variable
Figure 1 shows the results of the fuzzy regression model obtained with the original dataset, respectively with LS (left panel) and LMS-WLS (right panel). The results are very similar, as can be seen from the value of 
It can be noticed that the presence of whatsoever kind of outliers does not affect LMS-WLS estimates, as can be seen from Figures 2-6 and Table 1.
On the contrary, outliers heavily distort LS estimates. For example, in Figure 2(a) we see that the presence of a single outlier in m has troublesome effect on the fitting of the centers model to the data, and produces a large

Figure 1. Estimated model of the centers on the original dataset with LS (a) and LMS-WLS (b).

Figure 2. Estimated model of the centers with LS (a) and LMS-WLS (b) after contamination of m1 = 200.

Figure 3. Estimated model of the centers with LS (a) and LMS-WLS (b) after contamination of

Figure 4. Estimated model of the centers with LS (a) and LMS-WLS (b) after contamination of

Figure 5. Estimated model of the centers with LS (a) and LMS-WLS (b) after contamination of
bias in the parameter estimates of the centers models, as can be seen from the case (b) of Table 1. However, the parameter estimates for the models on the spreads are only slightly affected.
Figure 3(a) illustrates that the presence of single outlier in the spreads of the fuzzy response variable has little effect on the fitting of the centers model to the data, while the LS estimates for the spreads are heavily affected (Table 1, the case (c)). Note that the model fit to the data decreases to a lesser extent than in other situations, since, in the computation of 


The overall pattern of results remains the same also in the cases where there is an outlier in the spreads or centers of the fuzzy explanatory variable. When we contaminate data with single outlier in center or spread of input variables, LS estimates are distorted for the models of the centers (see Figure 4(a) and Figure 5(a)). We

Figure 6. Estimated model of the centers with LS (a) and LMS-WLS (b) after contamination of
can see from the cases (d) and (e) of Table 1 that the presence of single outlier in the centers of fuzzy input has bigger impact on the parameter estimates.
Finally, in Figure 6 we consider the more general situation embodies all previous cases. Both the models of centers and the models of spreads are strongly affected. As a consequence, also the fit performance of the model is quite poor.
As said before, Table 1 reports the parameter estimates for all the cases considered, both for the LS and LMS-WLS model.
6.2. Example 2
This example consists of 14 fuzzy observations with two fuzzy explanatory variables and one fuzzy response variable from Wu [27] , which is listed in Table 2. In this example, we set three different fuzzy numbers in the dataset, respectively, higher fuzzy extent, median fuzzy extent and lower fuzzy extent [28] . The setting is as follows:
LS and LMS-WLS estimates are reported in Table 3, in the first and second column respectively, obtained in correspondence to different types of outliers in the datasets.
LMS-WLS estimates do not noticeably change regardless of the absence or presence of outliers that is the same as the previou-s example, thus proving the effectiveness of the estimation procedure proposed.
If there is an outlier in the centers of output variable (Table 3, the case (b)), LS estimate of the coefficient vectors 

If we contaminate the vector X (Table 3, the case (c)) with a single outlier, LS produces biased estimates respectively for
If there is an outlier in the left spreads of output variable (Table 3, the case (d)), the estimates for 
When we consider the more general cases (Table 3, the case (g) and Table 3, the case (h)), LS estimates are strongly biased with respect to the estimates obtained with the original dataset. As a consequence, also the fit performance of model is quite poor.
Table 1. Estimated coefficients, 

7. Conclusions
The main problem that is investigated in this paper is to give a suitable method to deal with fuzzy data contaminated by outliers, the fuzzy extent of which may be different. In this regard, a fuzzy regression model with fuzzy output and fuzzy inputs has been proposed. Then on the basis of the Least Median Squares-Weighted Least
Table 2. Original data.
Table 3. Estimated coefficients, 

Squares estimation procedure, we introduce a robust version of the proposed model. In order to analyze the performance of our model, we also suggest a suitable goodness of fit index, and its adjusted version, which is effective for the model selection. The proposed model was applied in two examples, the results of which show that our model outperforms the fuzzy regression model estimated with LS method in the presence of different typologies outliers. In addition, the proposed model is applicable for all kinds of fuzzy numbers.
In the future, we will consider other robust regression approaches that usually are used in standard (non-fuzzy) regression analysis, for fuzzy linear regression analysis, such as the least trimmed squares. In addition, we will extend our robust fuzzy linear regression model with fuzzy inputs and output to robust non-linear regression models with fuzzy inputs and fuzzy output.
Cite this paper
Dan Zhang,Qiujun Lu, (2016) Robust Regression Analysis with LR-Type Fuzzy Input Variables and Fuzzy Output Variable. Journal of Data Analysis and Information Processing,04,64-80. doi: 10.4236/jdaip.2016.42006
References
- 1. Tanaka, H., Uejima, S. and Asai, K. (1982) Linear Regression Analysis with Fuzzy Model. IEEE Transactions on Systems Man and Cybernetics, 12, 903-907. http://dx.doi.org/10.1109/TSMC.1982.4308925
- 2. Diamond, P. (1988) Fuzzy Least Squares. Information Sciences, 46, 141-157. http://dx.doi.org/10.1016/0020-0255(88)90047-3
- 3. Shakouri, H. and Nadimia, R. (2009) A Novel Fuzzy Linear Regression Model Based on A Non-Equality Possibility Index and Optimum Uncertainty. Applied Soft Computing, 9, 590-598. http://dx.doi.org/10.1016/j.asoc.2008.08.005
- 4. Celmins, A. (1987) Multidimensional Least-Squares Fitting of Fuzzy Models. Mathematical Modelling, 9, 669-690. http://dx.doi.org/10.1016/0270-0255(87)90468-4
- 5. Chang, P.T. and Lee, E.S. (1996) A Generalized Fuzzy Weighted Least-Squares Regression. Fuzzy Sets and Systems, 82, 289-298. http://dx.doi.org/10.1016/0165-0114(95)00284-7
- 6. Chang, Y.H. (2001) Hybrid Fuzzy Least-Squares Regression Analysis and Its Reliability Measures. Fuzzy Sets and Systems, 119, 225-246. http://dx.doi.org/10.1016/S0165-0114(99)00092-5
- 7. Coppi, R. and D’Urso, P. (2003) Regression Analysis with Fuzzy Informational Paradigm: A Least-Squares Approach Using Membership Function Information. International Journal of Pure and Applied Mathematics, 8, 279-306.
- 8. Coppi, R., D’Urso, P., Giordani, P. and Santoro, A. (2006) Least Squares Estimation of a Linear Regression Model with LR Fuzzy Response. Computational Statistics and Data Analysis, 51, 267-286. http://dx.doi.org/10.1016/j.csda.2006.04.036
- 9. D’Urso, P. (2003) Linear Regression Analysis for Fuzzy/Crisp Input and Fuzzy/Crisp Output Data. Computational Statistics and Data Analysis, 42, 47-72. http://dx.doi.org/10.1016/S0167-9473(02)00117-2
- 10. D’Urso, P. and Gastaldi, T. (2000) A Least-Squares Approach to Fuzzy Linear Regression Analysis. Computational Statistics and Data Analysis, 34, 427-440. http://dx.doi.org/10.1016/S0167-9473(99)00109-7
- 11. Watada, J. and Yabuuchi, Y. (1995) Fuzzy Robust Regression Analysis Based on a Hyperelliptic Function. Journal of the Operations Research Society of Japan, 39, 512-524. http://dx.doi.org/10.1109/fuzzy.1995.409931
- 12. Yang, M.S. and Ko, C.H. (1997) On Cluster-Wise Fuzzy Regression Analysis. IEEE Transactions on Systems Man and Cybernetics Part B, 27, 1-13. http://dx.doi.org/10.1109/3477.552181
- 13. Oussalah, M. and De Schutter, J. (2002) Robust Fuzzy Linear Regression and Application for Contact Identification. Intelligent Automation and Soft Computing, 8, 31-39. http://dx.doi.org/10.1080/10798587.2002.10644195
- 14. Yang, M.S. and Liu, H.H. (2003) Fuzzy Least Squares Algorithms for Interactive Fuzzy Linear Regression Models. Fuzzy Sets and Systems, 135, 305-316. http://dx.doi.org/10.1016/S0165-0114(02)00123-9
- 15. Sanli, K. and Apaydin, A. (2004) The Fuzzy Robust Regression Analysis, the Case of Fuzzy Data Sethas Outlier. Gazi University Journal of Science, 17, 71-84.
- 16. Varga, S. (2007) Robust Estimations in Classical Regression Models versus Robust Estimations in Fuzzy Regression Models. Kybernetika, 43, 503-508.
- 17. Choi, S.H. and Buckley, J.J. (2008) Fuzzy Regression Using Least Absolute Deviation Estimators. Soft Computing— A Fusion of Foundations, Methodologies and Applications, 12, 257-263.
- 18. Kula, K.S. and Apaydin, A. (2008) Fuzzy Robust Regression Analysis Based on the Ranking of Fuzzy Sets. Inter- national Journal Uncertainty, Fuzziness and Knowledge-Based Systems, 16, 663-681. http://dx.doi.org/10.1142/S0218488508005558
- 19. Modarres, M., Nasrabadi, E. and Nasrabadi, M.M. (2004) Fuzzy Linear Regression Analysis from the Point of View Risk. International Journal Uncertainty, Fuzziness and Knowledge-Based Systems, 12, 635-649. http://dx.doi.org/10.1142/S0218488504003120
- 20. Modarres, M., Nasrabadi, E. and Nasrabadi, M.M. (2005) Fuzzy Linear Regression with Least Squares Errors. Applied Mathematics and Computation, 163, 977-989. http://dx.doi.org/10.1016/j.amc.2004.05.004
- 21. Nasrabadi, E. and Hashemi, S.M. (2008) Robust Fuzzy Regression Analysis Using Neural Networks. International Journal Uncertainty, Fuzziness and Knowledge-Based Systems, 16, 579-598. http://dx.doi.org/10.1142/S021848850800542X
- 22. Hu, Y.C. (2009) Functional-Link Nets with Genetic-Algorithm-Based Learning for Robust Nonlinear Interval Regression Analysis. Neurocomputing, 72, 1808-1816. http://dx.doi.org/10.1016/j.neucom.2008.07.002
- 23. Maronna, R.A. and Yohai, V.J. (2013) Robust Functional Linear Regression Based on Splines. Computational Statistics and Data Analysis, 65, 46-55. http://dx.doi.org/10.1016/j.csda.2011.11.014
- 24. D’Urso, P., Massari, R. and Santoro, A. (2011) Robust Fuzzy Regression Analysis. Information Sciences, 181, 4154- 4174. http://dx.doi.org/10.1016/j.ins.2011.04.031
- 25. Chachi, J. and Roozbeh, M. (2015) A Fuzzy Robust Regression Approach Applied to Bedload Transport Data. Communications in Statistics-Simulation and Computation, Online Publication Date: 7 April 2015. http://dx.doi.org/10.1080/03610918.2015.1010002
- 26. Wang, L. (2013) Robust Estimation Methods and Applicative Examples of Linear Regression Models. Master Thesis, Shandong University, Jinan.
- 27. Wu, H.C. (2003) Linear Regression Analysis for Fuzzy Input and Output Data Using the Extension Principle. Computers and Mathematics with Applications, 45, 1849-1859. http://dx.doi.org/10.1016/S0898-1221(03)90006-X
- 28. Ren, L.L. and Lu, Q.J. (2013) E-Commerce Trading Volume Forecast Based on Fuzzy Linear Regression. Statistics and Decision, 3, 31-34.





















