Journal of Data Analysis and Information Processing
Vol.03 No.04(2015), Article ID:61038,16 pages
10.4236/jdaip.2015.34012
Probabilistic, Statistical and Algorithmic Aspects of the Similarity of Texts and Application to Gospels Comparison
Soumaila Dembele1,2, Gane Samb Lo2,3
1LSTA, Université Pierre et Marie Curie, Paris, France
2LERSTAD, Université Gaston Berger de Saint-Louis, Saint-Louis, Sénégal
3Université des Sciences de Gestion de Bamako, Bamako, Mali

Copyright © 2015 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).


Received 11 August 2015; accepted 9 November 2015; published 12 November 2015

ABSTRACT
The fundamental problem of similarity studies, in the frame of data-mining, is to examine and detect similar items in articles, papers, and books with huge sizes. In this paper, we are interested in the probabilistic, and the statistical and the algorithmic aspects in studies of texts. We will be using the approach of k-shinglings, a k-shingling being defined as a sequence of k consecutive characters that are extracted from a text (k ≥ 1). The main stake in this field is to find accurate and quick algorithms to compute the similarity in short times. This will be achieved in using approxi- mation methods. The first approximation method is statistical and, is based on the theorem of Glivenko-Cantelli. The second is the banding technique. And the third concerns a modification of the algorithm proposed by Rajaraman et al. ([1] ), denoted here as (RUM). The Jaccard index is the one being used in this paper. We finally illustrate these results of the paper on the four Gospels. The results are very conclusive.
Keywords:
Similarity, Web Mining, Jaccard Similarity, RU Algorithm, Minhashing, Data Mining, Shingling, Bible’s Gospels, Glivenko-Cantelli, Expected Similarity, Statistical Estimation

1. Introduction
In the modern context of open publication, particularly in Internet, similarity studies between classes of objects become crucial. For example, such studies can detect plagiarism of books, articles, and other works (see [2] [3] for example). Also they may reveal themselves as decision and management tools. An other illustration of the importance of such a knowledge concerns commercial firms. They may be interested in similarity patterns between clients from different sites or between clients who buy different articles. In the same order of ideas, movies renting companies may try to know the extent of similarity between clients subscribing for violence films and those renting action films for example.
As a probability concept, the notion of similarity is quite simple. However, in the context of Internet, the data may be huge. So that the main stake is the quick determination of some similarity index. The shorter the time of computation, the better the case. So similarity studies should rely on powerful algorithms that may give clear indications on similarities in seconds. The contextualization of the similarity, and forming the sets to be compared, and the similarity computations may take particular forms according to the domains of application.
The concept of similarity has been studied and is still studied by researchers from a variety of disciplines (mathematics, web-mining, information sciences, applied sciences, etc.) from several point of views (theoricical, algorithmic, high dimension reduction, computer calculations, etc.). The following references on top of [2] [3] already cited, to cite a few, may help the reader to have a broad idea on this concept : Chen et al. [4] for visual similarity, Cha [5] for the use of density functions in similarity detection, Gower et al. [6] and Zezula et al. [7] for the metric space approach, Strehl et al. [8] , Formica [9] in the context of information sciences, Bilenko et al. [10] and Theobold et al. [11] for focus similarity on on large-web collections.
In this paper, we will be focusing on similarity of texts. This leads us to consider the approach of shinglings, that we will define in Section 2.
The reader is referred to Rajaraman et al. ([1] ) for a general introduction to similarity studies in the context of webmining. In their book, they provide methods of determination of approximated indices of similarity. Also, they propose an algorithm that we denote as RU (Rajaraman and Ullman). However, this algorithm has not been yet investigated in the context of probability theory, up to our knowledge. Furthermore, an evaluation of the performances of such algorithms on usual texts may be of relevance to justify such methods.
First, we want to review these methods in a coherent probabilistic and statistical setting allowing to reach later―all the aspects of similarity in this field. Then we will describe the RU algorithm in details. We will point out its redundant sides, from which a modified algorithm-denoted RUM (for RU modified) will be proposed.
To evaluate the studied techniques, the four Gospels will be used with the ends of study of similarity. The techniques will be compared in terms of speed, request of time, request of computer science resources, and request of accuracy.
The obtained results constitute a plea for improving these techniques when dealing with larger sizes.
Regarding Gospels study, our results seem to be conclusive, that is the fourth canonical Gospels are significantly similar.
This paper is organized as follows. In the next section, we define the similarity of Jaccard and its metric and probabilistic approaches. Section 3 is concerned with the similarity of texts. In Section 4, we discuss about computation stakes of similarity. In Section 5, we present different methods to estimate the similarity index. Finally in Section 7, we deal with applications of the described methods to the similarity between the four Gospels. We conclude the paper by giving some perspectives.
2. Similarity of Sets
2.1. Definition
Let A and B be two sets. The Jaccard similarity of sets A and B, denoted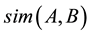 , is the ratio of the size of the intersection of A and B to the size of the union of A and B
, is the ratio of the size of the intersection of A and B to the size of the union of A and B
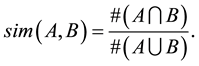 (1)
(1)
It is easy to see that for two identical sets, the similarity is 100% and for two totally disjoint sets, it is 0%.
2.2. Metric Approach
Let us consider a non-empty set S and its power set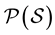 . Let us consider the application of dissimilarity
. Let us consider the application of dissimilarity

We have this simple result.
Proposition 1. The mapping d is metric.
Proof. Proving this simple result is not so obvious one might think. Indeed, special techniques are required to demonstrate the triangle inequality. This is done, for example, in ([6] ), page 15. Here, we just outline the other conditions for a metric:
1) First, let us show that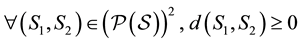 .
.
We have
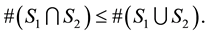
Then
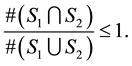
Next

Therefore
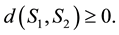
2) Let us show that . From (2.1), we get
. From (2.1), we get
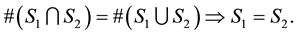
3) Let us remark that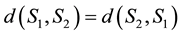 , since we have
, since we have , and
, and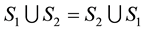 , that is: the roles of
, that is: the roles of
 and
and

So, studying of the similarity is equivalent to studying the distance of dissimilarity d between two sets. For more on the metric approach, see [7] .
2.3. Probabilistic Approach
Let us give a probabilistic approach of the similarity. For that, let us introduce the notion of the representation matrix. Let n be the size of the introduced set above.
Let us consider p subsets of S:

・ We form a rectangular array of

・ We put

・ We put in the column of S all the elements of S, that we might write from 1 to n in an arbitrary order.
・ In the column of each









An illustration of the matrix representation is given in Table 1.
Let us denote

This formula can be written also in the following form:
In the next theorem, we will establish that the similarity is a conditional probability.
Theorem 1. Let us randomly pick a row X among n rows. Let

Table 1. Representation matrix.





Proof. We first observe that for the defined matrix below, the set of rows can be split into three classes, based on the columns


1) The rows X such as we have



2) The rows Y such as we have




3) The rows Z such as we have



Let us show that
Clearly, the similarity is the ratio of the number of rows X to the sum of the numbers of rows X and the number of rows Y. The rows Z are not involved in the similarity between


Then, by dividing the numerator and the denominator by n, we will have
Hence, we get the result
This theorem will be the foundation of the statistical estimation of the similarity as a probability.
Important remark. When we consider the similarity of two subsets, say







2.4. Expected Similarity
Here we shall use the language of the urns. Suppose that we have a reference set of size n that we consider as an urn U. We pick at random a subset X of size k and a subset Y of size m. If m and k have not the same value, the picking order of the sets does have an impact on our results. We then proceed at the beginning by picking at random the first subset, that will be picked all at once, next put it back in the urn U (reference set). Then we pick the other subset. Let us ask ourselves the question: what is the expected value of the similarity of Jaccard?
The answer at this question allows us later to appreciate the degree of similarity between the texts. We have the following result.
Proposition 2. Let U be a set of size n. Let us randomly pick two subsets X and Y of U, of respective sizes m and k according to the scheme described above. We have

Further

Proof. Let us use the scheme described above. Let us first pick the set X. We have



Once

Since
The result corresponding to picking up Y first, is obtained by symmetry of roles of k and n. We then get (2). The formula (3) comes out immediately since

3. Similarity of Texts
The similarity is an automatic tool to anticipate plagiarisms, abusive quotations, influences, etc. However the study of the similarity of texts relies for instance on the words and not on the meanings.
3.1. Forming of Sets for Comparison
If we want to compare two texts




We observe a serious difficulty in the practice in using the notion of similarity defined on sets of k-shinglings. Indeed, when we consider the k-shinglings of a text, it is very probable that some k-shinglings will be repeated. Then the collection of k-shinglings cannot define a mathematical set (whose elements are supposed to be distinct).
But fortunately, a k-shingling is determined by its value and its rank. Suppose that a text has a length n. We can denote the k-shinglings by means of a vector t of




With this definition, the k-shinglings are different and do form a well-defined mathematical set.
3.2. Interpretation of the Similarity of Texts
Does the similarity between two texts have necessarily another explanation other than randomness? To answer to this question, let us remark that in any language, a text is composed from an alphabet that is formed by a finite and even small number of characters. A text in English is a sequence of lowercase and uppercase letters of the alphabet, of numbers and of some signs such as punctuations, apostrophes, etc. This set doesn’t exceed a hundred characters.
Suppose that the computed similarity between the two sets is




It is therefore important to have an idea of the value of


3.3. Implementation of the Algorithm for Computing the Similarity of Texts
Let A and B be two texts. For a fixed
and
The determination of the similarity between the two texts is achieved through comparing each k-shingling of A with all k-shinglings of B. We will have two problems to solve.
Suppose that a k-shingling is represented many times in B. We have the risk that the same value of this k-shingling in A is used as many times when forming the intersection between of k-shinglings sets. This would result in a disaster.
To avoid that, we associate to each k-shingling


It suffices to introduce the sentinel variables that identify if a k-shingling husband or a k-shingling wife has a wife or a husband at the moment of the comparison.
Let us introduce the vectors
and
We put



1. Set
2. Repeat for


2a. If
2b. Else
2b-1. Do for:


2b-11. If
2b-12. Else compare


2b-13. If equality holds, increment



2b-14. Else go to the next j.
3. Report the similarity
4. Computation Stakes
The search of similarity faces many challenges in the Web context and at the local post of personal computer.
4.1. Limitation of the Random Access Memory (RAM)
When we want to compare two sources of texts, each leading to a large number of shinglings, say










We are tempted to appeal to another method, that directly uses data from files. Here is how it works:
1) open the file of the text A;
2) read a row of the file A;
3) open the file B: read all these rows one by one and compare the k-shinglings of the file B with the k-shinglings at the current row of file A;
4) close the file B;
5) go to the next row of file A.
This method that we denote by the similarity by file does practically not use the RAM of the computer. We are then facing to two competing methods. Each of them has its qualities and its defects.
4.1.1. The Direct Method
It loads the vectors of k-shinglings in the RAM. It leads to quick calculations. However we have the risk to stuck the machine when the sizes of the files are huge.
4.1.2. The Method of Similarity by File
It spares the RAM of the machine and increases the computing speed. However it leads to considerable times of computations since, for example, the second file is opened as many time as the first contains rows. We spare the RAM but we lose time.
You have to notice that in the implementation of this method, we always have to carry the incomplete ends of each row at the next row.
Example 1. Suppose that we compare the 5-shinglings of the first row of A and the first row of B. The last four letters of the row cannot form a 5-shinglings. We have to use them by adding them at the first place of the second row of A. These additional ends are denoted “boutavant 1”s in the procedures done in (4.1), when we implement the similarity by file method. We do the same thing for the rows of B that give the “boutavant 2” s.
For example, in the work on the Gospel versions, where the numbers of k-shinglings are of the order of one hundred thousands, the method of similarity by file takes around thirty minutes and the direct method requires more or less ten minutes. We reduce the time of computation by three at the risk to block the RAM.
All what precedes advocates using approximated methods for computing similarity. Here, we are going to see three approaches but we only apply two of them in the study of the Gospel texts.
5. Approximated Computation of Similarity
5.1. Theorem of Glivenko-Cantelli
Since the similarity is a conditional probability in according to Theorem 1, we can deduce a law of Glivenko- Cantelli in the following way.
Theorem 2. Let p be the similarity between two sets of total size n. Let us pick at random two subsets of respective sizes








That is a direct consequence of the classical theorem of Glivenko-Cantelli. It then yields a useful tool. For example, for the similarity of Gospels for which the similarity is determined in more or less ten minutes, the random choice of subsets of size around ten thousand k-shinglings for each Gospel gives a computation time less than one minute, with an accuracy of 90%. To avoid the instability due to one random choice only, the average on ten random choices gives a better approximated similarity in more or less one minute. We will widely come back to this point in the applications.
5.2. Analysis of the Banding Technique
The banding technique is a supplementary technique based on the approximation of Theorem of Glivenko- Cantelli. Suppose that we divide the representation matrix, in b bands of r rows. The similarity can be computed first by considering the similarity between the different rows of one band then, between some bounds only. We do not use this approach here.
5.3. The RU Algorithm
It is based on the notion of minhashing to reduce documents of huge sizes into documents of small sizes called signatures. The computation of the similarity is done on their compressed versions, i.e. on their signatures. To better explain this notion, let us consider p subsets of a huge reference set and let us use the matrix be defined in Table 2.
The similarity between two sets is directly got as soon as this table is formed by using the formula (2.1) in a quick way. But the setting of this matrix takes time. This is serious drawback of the original RU algorithm that we will describe soon. For the moment, suppose that the table exists. On this basis, we are going to introduce the RU algorithm. By this algorithm, we do three things. First, we consider an arbitrary permutation of the rows. Then, we replace the columns transformations called minhashes by means of congruence functions. Then, a new table is formed to replace the original table. This new and shorter one, that we describe immediately below, is called signature matrix.
5.3.1. Minhashing Signature
Suppose that the elements of S are given in a certain order denoted from 1 to n. Let us consider p functions




where



The RU algorithm replaces this matrix by another smaller one called minhashing signature, represented in Table 4.
Table 2. Subsets representation matrix.
Table 3. Completition of the representation matrix by minhashing columns.
Table 4. Signature matrix.
To fill in the table above, Anand et al. ([1] ), page 65, propose the algorithm below:
Algorithm of filling of the columns
1. Set all the


2. For each column
2-a. For each element i, from 1 to n, compute
2-b. If i is not in

2-c. If i is in


2-d. Go to
3. Go to
4. End.
At the end of the procedure, each column will contain only integers between 1 and n. The computed simi- larity on this compressed table between



However, we can simplify this algorithm in a very simple way, by saying this.
Criterion 1. The transpose of the column
coordinate,


This simple remark allows to set up programs in a much easier way.
5.3.2. The RUM Algorithm or the Modified RU Algorithm
It is clear that by forming the matrix of Table 2, the similarity is automatically computed. Indeed, when we consider the columns






1) Form one set S by putting the elements of



2) Apply the RU algorithm at this collection by using Criterion 1.
We do not seek to find the intersections. Elements of the intersection are counted twice here. But it is clear that we still have a zero similarity index if the two sets


The question is: how well the estimations of the similarity using RU or RUM algorithm are good approxi- mations of the true similarity index? In this paper, we give an empirical response based on the Gospels comparison by showing that the RUM approximation of the similarity of good while performing only in a few seconds in place of thirty minutes (1.800 seconds)!
The exact distribution of the RUM index is to be found depending on the laws of the stochastic laws of the coefficients


6. The Applications of the Similarity of the Bible Texts
6.1. Textual Context of the Four Versions of the Gospels
Here, we are going to resume a few important points for the backgrounds of our Gospels analysis. In all this subsection, we refer to [12] [13] .
The Gospels (In Latin, Gospel means good news) are texts that relate the life and the teaching of Jesus of Nazareth, called Jesus Christ. Four Gospels were accepted as canonical by the Church: the Gospel according to Matthew, to Mark, to Luke and to John. The other unaccepted Gospels are qualified apocryphal ones. Numerous Gospels have been written in the first century in our era. Before to be consigned as written, the message of Christ was verbally transmitted. From tale stories, many texts were composed, among which the four Gospels that were retained in the Biblical canon. The canonical Gospels are anonymous. They were traditionally attributed to disciples of Jesus Christ. The Gospel according to Matthew and the Gospel according to John would have been from direct witnesses of the preaching of Jesus. Those of Mark and Luke are related to close disciples.
The first Gospel is the one attributed to Mark. It would have been written in about 70 years AD. In about 80 - 85, follows the Gospel according to Luke. The Gospel according to Matthew is dated between 80 and 90, and to finish, the one of John is dated in between 80 and 110. However, these uncertain dates vary according to the authors that propose chronologies of the evangelical texts. The original Gospels were written in Greek.
The Gospel according to Matthew, Mark and Luke are called synoptic. They tell the tale of Jesus in a relatively similar way. The Gospel according to John is written using another way of taling Jesus’ life and mission (christology) qualified as Johannist. The first set of Gospel that has been written seems to be Mark’s one. According to some researchers, the common parts between Matthew and Luke Gospels may depend on a more older text that was lost. This text is referred as the Q source.
The source Q or Document Q or simply Q (The letter is from the German word QUELLE, meaning source) is a hypothetical source, of whom some exegetes think it would be at the origin of common elements of Gospels of Matthew and Luke. Those elements are absent in Mark. It would be a collection of words of Jesus of Nazareth that some biblists attempted to reconstitute. This source is thought to date around of 50 AD.
The Gospels of Matthew and Luke are traditionally influenced by Mark’s Gospel and the Old Testament. But though separately written, they have in common numerous extracts that don’t come from the two first cited sources. This is why the biblists of XIXe century generally think that these facts suggest the existence of a second common source, called “document Q”. Since the end of XIXe century, Logia (i.e. the speech in Greek) seems to have been an essentially collection of speeches of Jesus. With the hypothesis of the priority of the Gospel of Mark, the hypothesis of the existence of the document Q is part of what the biblists call the hypothesis of two sources.
This hypothesis of two sources is the most general solution that is accepted for the synoptic problem, that concerns the literary influences between the three canonical Gospels (Mark, Matthew, Luke), called Synoptic Gospels. These influences are sensitive by the similarities in the choice of words and the order of these words in the statement. The synoptic problem wonders about the origin and the nature of these relationships. From the hypothesis of two sources, not only Matthew and Luke learned all both on the Gospel according to Mark, independently one to other; but as we detect similarities between the Gospels of Matthew and Luke, that we cannot find in the Gospel of Mark, we have to suppose the existence of a second source.
Synoptic Gospels
The Gospels of Matthew, Mark, and Luke are considered synoptic Gospels on the basis of many similarities between them that are not shared by the Gospel of John. Synoptic means here that they can be seen or read together, indicating the many parallels that exist among the three.
The Gospel of John, on the contrary has been recognized, for a long time as distinct of first three Gospels so much by the originality of its themes, of its content, of the interval of time that it recovers, and of its narrative order and the style. Clément of Alexandria summarized the single character of the Gospel of John by saying: John came last, and was conscious that the terrestrial facts had been already exposed in the first Gospel. He composed a spiritual Gospel.
Indeed, the Gospel of John, presents a very different picture of Jesus and his ministry from the synoptics. In differentiating history from invention, some historians interpret the Gospel accounts skeptically but generally regard the synoptic Gospels as including significant amounts of historically reliable information about Jesus. The common parts of the Gospels of Matthew and of Luke depend on an antiquarian document but lost called source Q according to some researchers.
The synoptic Gospels effectively have many parallels between them: thus around 80% of verses of Mark may be found in Matthew and Luke Gospels. As the content is in three Gospels, one talks about of Triple Tradition. The passages of the Triple Tradition are essentially narrations but we can find in it some speeches of Christ.
But otherwise, we also find numerous identical passages between Matthew and Luke, but absent in the Gospel of Mark. Almost 25% of verses of the Gospel according to Matthew find an echo from Luke (but not from Mark). The common passages between Matthew and Luke are mentioned as the Double Tradition.
The four Gospels constitute the principle documentary concerning the life and the teachings of Christ. Each of them uses a particular perspective. But all of them use the same general scheme and convey the same philosophy. We stop here. For further details see [?]. We will attempt to explain the results in our own analysis of similarity below.
6.2. The General Setting
All the computations were done in the environment of VB6R. Once the four texts are chosen, we follow these steps. We first proceed to the editing files by dropping the words of less than three letters. Then we proceed to the computations of the similarity between the different Gospels.
Next, we find for each gospel, the number of the rows of files as well as the number of letters.
Table 5 gives the numbers of the rows, before and after editing, of each Gospel.
Now we are going to report the common numbers of k-shinglings with

The results are in Table 6 and Table 7.
Approximated Similarity
In this part, the computation of the similarity will be done by the direct method. Let us pick randomly 10,000 k-shinglings from first file and 10,000 k-shinglings from the second file. We remark that the time of com- putation of the similarity turns around 20 seconds. We get approximated values of similarities between the Gospels. Let us use the two methods of computation through a double approximation of the similarity i.e. approximation using the theorem of Glivenko-Cantelli and of the RUM algorithm. The results are given in Table 8.
This approach is simply extraordinary since we may use a very low number of hash functions (pp) and get good approximations. To guarantee the stability of the results, we report the average results got for

Table 5. Total numbers of rows and letters of the synoptic Gospels.
Table 6. Computation durations of the exact Jaccard similarity beetwen two Gospels by using the direct methods.
Table 7. Computation durations of the exact Jaccard similarity beetwen two Gospels by using the file method.
Table 8. Computation durations of the approximated Jaccard similarity beetwen two Gospels by using the glivenko-cantelli theorem.
6.3. Analysis of Results
6.3.1. Evaluation of Algorithms on the Similarity by the Direct Method
In this algorithm, we first form the k-shinglings sets for each text. Then we compute the similarity between them.
We remark that the time of the determination of the similarity between the different Gospels turns around ten minutes. The different similarity amounts are around 50%.
1) Algorithm on the similarity by the method by file
Here we remark that the times of the determination are much greater than those in the case of the similarity by the direct method. The time turns around 30 minutes. We naturally have the same similarities already given by
Table 9. Computation durations of the approximated Jaccard similarity beetwen two Gospels by using the RUM algorithm with pp = 5 minhashing functions.
Table 10. Computation durations of the approximated Jaccard similarity beetwen two Gospels by using the RUM algorithm with pp = 10 minhashing functions.
Table 11. Computation durations of the approximated Jaccard similarity beetwen two Gospels by using the RUM algorithm with pp = 15 minhashing functions.
the direct method.
2) Algorithm on the similarity by the theorem of Glivenko-Cantelli
We randomly pick a number

Table 12. Computation durations of the approximated Jaccard similarity beetwen two Gospels by using the RUM algorithm with pp = 20 minhashing functions.
We remark a considerable reduction of the time of the determination of the similarity. The result is huge. The similarity indices are got in less a minute. The similarity also turns around 50%.
3) RUM Algorithm for the similarity computation
We randomly pick


Finally, we arrive at a tuning result: by using subsamples of the two sets and by using the approximation method via the RUM algorithm, we get an acceptable estimation of the similarity in a few number of seconds. But since the results may be biased, performing the process a certain number of times and reporting the average is better.
We may study the variability of the results. If we proceed


For the Gospels for example, we finally conclude that the true estimation of the similarity is in an interval centered at the approximated value given by the RUM method with magnitude 10%. This result, that is achieved only in seconds, is very significant for large sets.
We may also appreciate the power of this algorithm that allows estimation of the similarity of set around one hundred thousand (100.000) characters in only 6 seconds.
6.3.2. Comparison of Gospels
From the Tables 9-12, we notice that the Gospels of Luke and Matthew have the greatest similarity around 70%. From what we already said in Subsection 6.1, Luke and Matthew have used the Gospel of Mark and in addition, are based on unknown source Q. Likewise the similarity between the Gospel of John and the others might explained by the fact that the John Gospel is the last to be released in about year 100 or year 110 of our era. He might already be aware of the contents of the other three gospels.
We might hope to have a similarity around 90%. But many factors can influence on the outcomes. Actually, the Gospels are written by four different persons. Each of them may use his own words. Besides, we used translated versions. This latter fact can result in a significant decrease of the true similarity. An other point concerns the fact that a limited alphabet is used. This in turn is in favor of forming a structural part in the similarity. For example, for the considered sizes, this part is around 30%.
With the order of the sets sizes, we have the automatic and stochastic similarity of order of 30%. Since the similarities turn around 50% between the Gospels, we conclude that Gospels really have a significant similarity. By taking account the remarks that have been made above, we may expect that these similarities should be really much greater. This is in favor of the hypothesis of the existence of a common source that can be denamed as the source Q.
6.3.3. Recommendations and Perspectives
To conclude we recommend these following steps in assessing similarity:
1) Determine the automatic and stochastic part of the similarity, by simulation studies by using formula (4);
2) Form the sets of k-shinglings of the two studied sets;
3) Pick at random


4) Apply the RUM algorithm;
5) Compare the finding similarity with the results of the point (1);
6) Conclude on a significant similarity if the reached similarity, is widely superior tothe stochastic similarity determined in (1). Otherwise the similarity is not accepted;
7) Apply the RUM algorithm a number of times before doing definitive conclusion.
6.3.4. Conclusions
In this paper, we described the main methods of determination of the similarity. We empirically estimated the incompressible stochastic similarity between two texts. We proposed a modification of the RU algorithm, named RUM, and we applied on subsamples of the studied texts. The combination of the Glivenko-Cantelli theorem and an empirical study of the RUM algorithm, led to the conclusion that the approximated similarity that was given by this procedure, was a good estimation of the true similarity. Since this approximated similarity was computed in seconds, the method showed remarkable performance. Hence it was recommended for the study of similarity for very large data sets.
We applied our methods to the four Gospels. The obtained results concerned the study of Gospels themselves as well as the evaluation of different methods of computation of the similarity. In conclusion, the Gospels had indices of similarity at least 50%.
In a coming paper, we would concentrate on the theoretical foundations of the RUM algorithm in the setting of Probability Theory and Statistics.
Acknowledgements
The reviewer drew our attention on profound sights and interesting facts about the Gospels writing history. For example, he pointed out that for each gospel, there are several authors, each of them providing a contribution. He also drew to our attention on other methods for texts analysis. As he concluded himself, this text is data analysis oriented. The Bible’s Gospels has been used as a material on which the theory is illustrated. The ideas, the suggestions and the points of views he provided will certainly be extensively used in the final version of the PhD dissertation of the first author.
The first author thanks the Programme de formation des formateurs des Universités de Bamako which financed his stays in the LERSTAD of UGB while preparing his PhD dissertation. The authors acknowledge support from the Réseau EDP-Modélisation et Contrôle, of Western African Universities, that financed travel and accomodation of the second author while visiting USTTB in preparation of this work.
Cite this paper
SoumailaDembele,Gane SambLo,11, (2015) Probabilistic, Statistical and Algorithmic Aspects of the Similarity of Texts and Application to Gospels Comparison. Journal of Data Analysis and Information Processing,03,112-127. doi: 10.4236/jdaip.2015.34012
References
- 1. Rajaraman, A. and Ullman, J.D. (2011) Mining of Massive Datasets. Cambridge University Press, Cambridge. http://dx.doi.org/10.1017/cbo9781139058452
- 2. Stein, B. and Eissen, S.M. (2006) Near Similarity Search and Plagiarism Analysis. In: Spiliopoulou, et al., Eds., From Data and Information Analysis to Knowledge Engineering Selected Papers from the 29th Annual Conference of the German Classification Society (GfKl) Magdeburg, Springer, Berlin Heidelberg, 430-437. http://dx.doi.org/10.1007/3-540-31314-1_52
- 3. Gionis, A., Indyk, P. and Motwani, R. (1999) Similarity Search in High Dimensions via Hashing. Proceedings of the 25th VLDB Conference, Edinburgh, Scotland, 1999, 518-529.
- 4. Chen, D.-Y., Tian, X.-P., Shen, Y.-T. and Ouhyoung, M. (2003) On Visual Similarity Based 3D Model Retrieval. Eurographics 2003, 22, 223-232.
- 5. Cha, S.H. (2007) Comprehensive Survey on Distance Similarity Measures between Probability Density Functions. International Journal of Mathematical Models and Methods in Applied Sciences, 4, 300-307.
- 6. Gower, J.C. and Legendre, P. (1986) Metric and Euclidean Properties of Dissimilarity Coefficients. Journal of Classification, 3, 5-48. http://dx.doi.org/10.1007/BF01896809
- 7. Zezula, P., Dohnal, V. and Amato, G. (2006) Similarity Search the Metric Space Approach. Advances in Database Systems, Springer Series, 32, 220 p.
- 8. Strehl, A., Ghosh, J. and Mooney, R. (2000) Impact of Similarity Measures on Web-Page Clustering. American Association for Artificial Intelligence, 78712-1084.
- 9. Formica A. (2005) Ontology-Based Concept Similarity in Formal Concept Analysis. Information Sciences, 176, 2624-2641.
- 10. Bilenko, M. and Mooney, R.J. (2003) Adaptive Duplicate Detection Using Learnable String Similarity Measures. Proceedings of the 9th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining (KDD), Washington DC, 2003, 39-48, http://dx.doi.org/10.1145/956750.956759
- 11. Theobold, M., Siddharth, J. and Paepcke, A. SpotSigs: robust and efficient near duplicate detection in large web collections. Proceedings of the 31st Annual International ACM SIGIR Conference on Research and Development in Information Retrieval, Singapore, 2008, 563-570.
- 12. http://fr.wikipedia.org/wiki/évangiles
- 13. http://www.info-bible.org/lsg/INDEX.html














