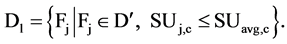Journal of Data Analysis and Information Processing
Vol.02 No.04(2014), Article ID:51490,10 pages
10.4236/jdaip.2014.24012
A Feature Subset Selection Technique for High Dimensional Data using Symmetric Uncertainty
Bharat Singh, Nidhi Kushwaha, Om Prakash Vyas
Department of Information Technology, Indian Institute of Information Technology, Allahabad, India
Email: bharatbbd1@gmail.com, kushwaha.nidhi12@gmail.com, dropvyas@gmail.com
Copyright © 2014 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 18 September 2014; revised 20 October 2014; accepted 11 November 2014
ABSTRACT
With the abundance of exceptionally High Dimensional data, feature selection has become an essential element in the Data Mining process. In this paper, we investigate the problem of efficient feature selection for classification on High Dimensional datasets. We present a novel filter based approach for feature selection that sorts out the features based on a score and then we measure the performance of four different Data Mining classification algorithms on the resulting data. In the proposed approach, we partition the sorted feature and search the important feature in forward manner as well as in reversed manner, while starting from first and last feature simultaneously in the sorted list. The proposed approach is highly scalable and effective as it parallelizes over both attribute and tuples simultaneously allowing us to evaluate many of potential features for High Dimensional datasets. The newly proposed framework for feature selection is experimentally shown to be very valuable with real and synthetic High Dimensional datasets which improve the precision of selected features. We have also tested it to measure classification accuracy against various feature selection process.
Keywords:
High Dimensional Datasets, Feature Selection, Classification, Predominant Feature

1. Introduction
Data Mining is a multidisciplinary task to find out hidden nuggets of information from data. In recent years, as the technology advances in various fields, the data generated in these fields, have become increasingly larger in both number of instances and number of features in various field. The proliferation of High Dimensional data in various applications poses challenges to Data Mining field. This enormity cause serious problems to many Data Mining and Machine Learning algorithms with respect to scalability and learning performance [1] . Feature selection is an active field of research and development since the 70’s, in multidisciplinary field. It includes statistical pattern recognition [2] [3] , machine learning [4] - [7] , Data Mining [8] - [10] and it is extensively applied to various field such as text categorization [11] [12] image retrieval [13] [14] , genomics analysis [7] [15] [16] , CRM [17] . Due to these applications, not only the datasets get larger, but different and new kinds of data are also generated, for example, stream data, microarray in proteomics and genomics, social computing and system biology datasets.
Within this, High Dimensional datasets are flattering more and more copious in learning process. Relatively it has made traditional search algorithm too expensive in terms of time and memory storage resource. Thus, several modification or enhancement to local search algorithm can be found to deal with such problem. Therefore, feature selection is indispensable for the Data Mining and Machine Learning process while managing High Dimensional datasets. Various established search techniques have shown promising results in a number of feature selection problems, but there are only few techniques which deal with High Dimensional data. The central hypothesis is that the important attribute sets are strongly correlated with the target class, and uncorrelated attributes are less important. Further, strong correlation among attribute with other attributes makes strong only one of them and other can be removed. If two or more attributes have the same importance to the target class values, it will be good to consider only one of them. As the attributes of a particular application increases, the dimension of that dataset increases. Then feature selection algorithm becomes intractable for finding the best subset, so this problem, sometimes becomes the NP-hard.
Feature selection is a simple method that tries to find out a subset of original features that have the same information regarding the whole datasets, without the loss of generality. Here, the main goal is to identify a few features/genes from thousands of genes to identify a specific set features/gene for specific diseases. However, as the number of attributes becomes extremely larger, most of these presented techniques face the problem of unachievable time computation. In this context, the main problem with this type of data is due to less number of instances, within hundred, while the number of feature is in the order of thousands or even in order of millions. The major challenge in these types of applications is to haul out a set of impressive features, as small as possible, that accurately classifies the learning algorithms [18] . In various Data Mining tasks, the input is represented by a very large number of features, many of which are not required for classifying the class. Feature selection is the task of choosing a small subset of features that is sufficient to classify the target class effectively. The main rea- son to use feature selection is to reduce computational cost, improved accuracy, and problem understanding.
From the study, there is no feature selection method available for handling the all requirement presents in the inconsistent real world datasets. So the hybrid methods were also present for improving the efficiency of this method. Ranking of features is also applicable for managing the number of large set of feature. After ranking all the features we select only features that are above then some threshold value and then apply our traditional Data Mining approaches on the reduced features to check its correctness and accuracy of the trained model with the reduced set of features.
The motivation for investigating the feature subset selection algorithms came from the requirement to give support to application domain experts with very important quantified evidence that the selected features ultimately become more robust to variations in the training data. This requirement is particularly decisive in biological applications, e.g. DNA-microarrays, genomics, and proteomics, mass spectrometry. These applications are generally characterized by high dimensionality; the goal is to find a small output set of highly uncorrelated variables on which biomedical and Data Miner experts will subsequently invest considerable less time and research effort.
The remaining of this paper is organized as follows. In section 2 we give the related work and background of feature selection techniques that are required for our proposed algorithm. Section 3 details the methodology and correlation based feature subset selection for High Dimensional data using SU. In section 4 we have presented our framework and algorithm. In the section 5 we have done complexity analysis of the proposed algorithm. Then, we have analyzed our algorithm’s result, on synthetic data as well as on real world data in section 6, and finally we conclude in section 7.
2. Literature Review and Background
The recent problem in Machine Learning and Data Mining is to discovering representative set of attributes from which to construct a model for classifying or clustering for a specific task. The Feature selection aims at selection a small subset of feature that meets certain criteria given by the user [15] [16] [18] - [20] . It reduces the number of attribute, separate out the irrelevant, noisy and redundant data, that improve and speed up the Data Mining techniques like prediction accuracy of classification. The central hypothesis is that the important attribute sets are strongly correlated with the class values, and uncorrelated attributes are less important. Further, strong correlation among attribute with other attributes makes strong only one of them and other can be removed. If two or more attributes having the same importance to the target class values then it will be good to consider only one of them.
In literature, a large number of feature selection algorithms have been already proposed and they were applied to different fields: bioinformatics [19] , text categorization [11] [12] , image processing [13] [14] , etc. Various taxonomies can be found in the literature in order to classify feature selection algorithms [9] . These algorithms can be of three models: Filter model, Wrapper model, and Embedded model. Filter model does not consider any Data Mining algorithm. They are strongly relies on underlying characteristics of the data variable depends on certain criteria. For example feature selection using, information gain [7] , fisher score, Laplacian score; these are methods to find features with the largest information gain, fisher score, Laplacian score respectively. These methods have some limitation as most of the methods are univariate. Consequently, each feature is considered individually without consideration of correlation among features. Wrapper model consider a learning process. Its aim to select a subset of feature that is used to predict or classify efficiently, that gives more discriminative power with that particular learning process; therefore, it consume more time compare to filter. The advantage of wrapper techniques is the suitably used the correlation among the features and the simultaneously interaction with the learning process. However, this type of algorithm has some limitations as it require very large calculation and computation. To overcome the wrapper model, we found very few algorithms in literature, which combine filter and wrapper search to benefit from the singular advantages of each methodology. But, in this paper, we will only consider filter-based approach. And, based on ranking of feature, we will select important attribute which are not redundant and whose SU value is greater than a particular threshold value.
In the process of feature selection, the most important and necessary key operation is, how the individual feature are clearly discriminated. For evaluation of discrimination power of attribute various methods have been proposed, in which information gain is the older and often used techniques [21] . Ding et al. [19] used mutual information gain for feature selection from biological dataset i.e. Microarray Gene Expression data.
A characteristic feature selection method consists of four fundamental steps as depicted in Figure 1, namely, generation of all possible subset, evaluation of generated subset, stopping criterion, and validation of result [10] . Generation of all possible subset is a brute force method that generates candidate feature subsets for estimation based on a particular search procedure. Each generated candidate feature subset is estimated and compared with the preceding most excellent one according to a certain estimating criterion [10] . If the criteria score of new subset come out to be better, it replaces the previous best subset. The process of generation of subset and estimation is recurring until a given stopping criterion is not satisfied [10] . Then, the most excellent subset usually needs to be tested by prior knowledge or many separate tests on synthetic datasets and/or real-world datasets. Feature selection can be found in various areas of Data Mining and Machine Learning such as classification, clustering, association rules, and regression with different applications in different domain [10] .
Figure 1. Four basic steps of feature selection.
Almuallim and Dietterich proposed FOCUS [22] , an exhaustive search algorithm, in this they showed that FOCUS can find the important and required features in quasi-polynomial time, but having some constraint like:
1) Limitation of difficulties in target class;
2) Data is free from the noise.
But the main problem in High Dimensional data is the computational complexity, that can be as large as O(2p), for example when all the features are relevant, it may be intractable. Devijver and Kittler in their paper review heuristic search algorithm. They have find Sequential Forward Selection (SFS) and Sequential Backward Selection (SBS) algorithms. These algorithms totally based on heuristic, “find out the most important attribute to add in every step of the iteration is the attribute to be selected and find out the most important attribute to remove in every step of the iteration is the attribute rejected”. These techniques cause problem with High Dimensional data because they did not consider the interaction among attributes.
Relief [23] has been a fundamental and traditional technique for feature selection for normal datasets but when handling High Dimensional data, it failed due to infeasibility of computation. An optimization using supervised model construction has been proposed to improve starter selection. Relief is a basic technique which depends on near-hit, near-miss and some statistical techniques for an instance. It is also noise tolerance and could be untouched by interaction of feature.
2.1. Mutual Information
How to measure the correlation between two or more attributes based on label data? Mutual information (MI) is a basic technique to measures how much knowledge between two attributes are correlated. It is defined as the difference between the sum of the marginal entropies and their joint entropy. For two totally independent objects the mutual information is always zero. In [20] , maximum dependency condition based on MI is used for feature selection, and various implementations for classification accuracies have been done. In this paper, we use mutual information, where Shannon’s entropy is utilized [20] .
Consider the High Dimensional data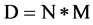 , where M is the number of feature and N is the number of the instances. Let x and y be two random features or variables, p(x) and p(y) be their probability density functions and p(x, y) be their joint probability density function. Then their mutual information (MI) has been defined as follows [24] :
, where M is the number of feature and N is the number of the instances. Let x and y be two random features or variables, p(x) and p(y) be their probability density functions and p(x, y) be their joint probability density function. Then their mutual information (MI) has been defined as follows [24] :
 (1)
(1)
We can use the relation of entropy and mutual information to solve the problem in different ways, these are as follow. Let H(X) denote Shannon’s entropy of X, then
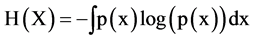 (2)
(2)
The entropy is related to mutual information as follows:
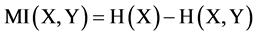 (3)
(3)
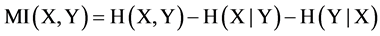 (4)
(4)
The feature’s values are considered to be discrete. Here, the marginal entropies is represented by H(X) and H(Y), 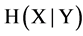 and
and 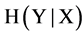 are the conditional entropies, and the joint entropy of X, Y is represented by H(X, Y). Mutual information is a symmetric estimation. That is the amount of mutual information with the relation with Y is equal to the amount of mutual information after observing X. We can say that the sequence of calculation for two variable X and Y (e.g., (x, y) or (y, x)) will not change the measurement.
are the conditional entropies, and the joint entropy of X, Y is represented by H(X, Y). Mutual information is a symmetric estimation. That is the amount of mutual information with the relation with Y is equal to the amount of mutual information after observing X. We can say that the sequence of calculation for two variable X and Y (e.g., (x, y) or (y, x)) will not change the measurement.
As a feature selection criterion, the best feature will maximize the mutual information MI(X, Y), where X is the feature vector and Y is the class indicator. This is a nonlinear statistics of correlation between feature values and class values. The symmetric uncertainty (SU) [1] [7] [16] [19] , is extended from MI with normalizing it to the entropy value of features and entropy value of features with class label. SU has been used to evaluate the effectiveness of features for classifying the data by various number of researchers [4] [13] [15] [16] [20] . Our approach also based on SU for correlation between either two features or a feature and a class value.
2.2. Symmetric Uncertainty
Symmetric uncertainty can be used to calculate the fitness of features for feature selection by calculating between feature and the target class. The feature which has high value of SU gets high importance. Symmetric uncertainty defined as
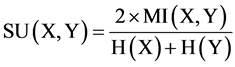 (5)
(5)
where H(X) is the entropy of a discrete random variable X. If the prior probability of each element of X is p(x), then H(X) can be calculated by equation (2).
Symmetric uncertainty, equation (5), behave a couple of variables symmetrically, it compensates for mutual information’s bias towards features having large number of different values and normalizes within range [0, 1]. A value 1 of SU(X, Y) indicate that knowledge of the object value strongly represent the values of other and the SU(X, Y) value 0 indicate the independence of X and Y. In this paper, we also deal with continuous features by normalized in proper discrete form.
2.3. Relevant Feature and F-Correlation
The definition of relevant feature is defined as: Fi is relevant to the target concept C if and only if there exists
some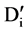 ,
, 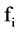 , and c, such that, for probability
, and c, such that, for probability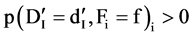 ,
, 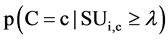 otherwise, feature
otherwise, feature
 is an irrelevant feature [1] . Definition of relevant Feature indicates that there are two type of relevant features due to different
is an irrelevant feature [1] . Definition of relevant Feature indicates that there are two type of relevant features due to different :
:
1) When , from the above definition, we can know that Fi is fundamentally relevant to the target class;
, from the above definition, we can know that Fi is fundamentally relevant to the target class;
2) When 
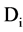
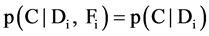
It can be concluded that 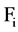
Given SU(X, Y) the symmetric uncertainty of features X & Y, the correlation between two attributes is refers
as F-correlation. The correlation between any pair of attributes 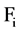
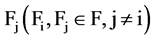
relation of 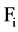
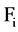
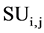
3. A Correlation Based Feature Subset Selection Algorithm
In this section, we propose the framework of our feature subset selection techniques which can improve the classification and clustering technique. To select important feature for classification or clustering accuracy, we require some aspect i.e.
· How to decide which of the attributes is relevant for a particular class and which of the all attributes are not?
· How to decide among all relevant which attribute is redundant?
· How to decide whether two attribute are closely correlated?
Using the symmetric uncertainty (SU) as the fitness function, we are able to generate an algorithm and framework to select important features for Data Mining task. This framework and algorithm is totally based on the correlation analysis of attributes using supervised High Dimensional datasets.
The answer to these questions can be sorted out by applying appropriate approaches, like, for first question we can use a user defined threshold value, generally used with filter approach of feature selection. For example, let us consider a dataset D having M feature and N instances and set of C classes. Let 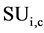
value, which is the second step in our framework. It can be defined as: 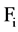
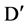
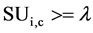
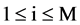
The answer to the next question is important because this is the main question on which we are focusing. For this, we have to analyze pair-wise correlations among all attributes, but if we calculate the pair wise correlation, the time complexity for this will be O(M2), where M is the number of attributes which are very high in High Dimensional data.
Correlation between attributes are also captures by symmetric uncertainty values, but to decide and differentiate between relevant and redundant attribute, we have a reason, why we are selecting a particular threshold value. We can say, need to define whether the value of correlation or symmetric uncertainty between two attributes in 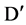
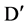
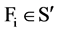
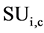
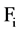
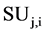
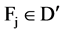
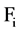
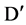
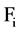
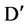
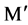
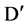
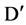
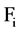
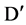
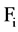
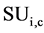
The correlation between a feature 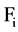
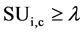
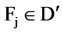
there should not be any 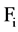
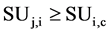
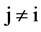
If there exists such 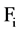
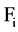
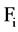
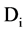
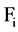
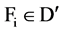
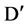
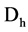
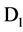
where 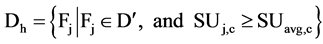
According to the above definitions, a attribute is good if it is predominant in predicting the class value, and feature selection, for classification, is a process that determine all predominant attributes to the class value and remove other attributes.
We are considering some assumptions in development of this framework, that is, if two attributes are seems redundant to each other and we have to remove one attribute, then we will remove the attributes that is less relevant to the class value and keeps more information to predict the class. The attribute with the highest 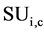
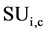
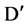
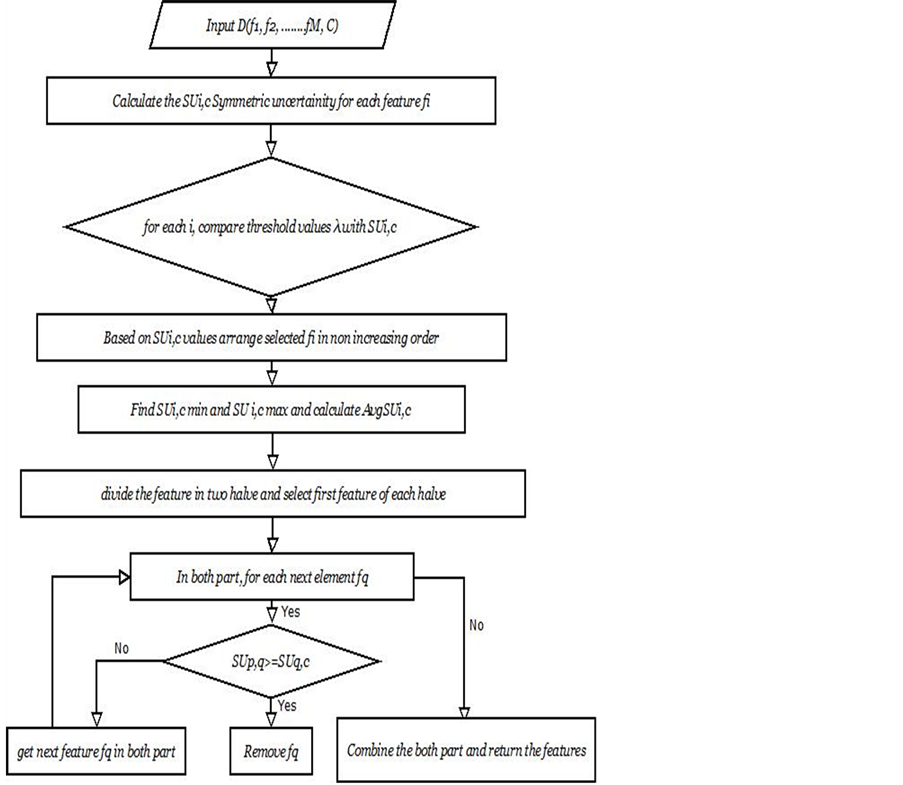
4. Proposed Framework and Algorithm
As we discussed the methodology so for, we are now going to propose a framework and algorithm. By using SU, that reimburse for the Information Gain’s bias toward attributes with more values and normalize their values in the range of [0, 1] where the value 1 represent the knowledge of either one of the values totally classify the value of the another and value 0 represent that X and Y are independent. The main advantages of using symmetric uncertainty are that it treats a pair of feature symmetrically.
We are using the SU value for two main reasons: as we can see in step two, it can remove the attributes that have less SU value than predefined threshold λ because those attribute which are having high 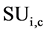
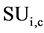
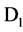
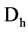
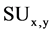
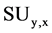
Figure 2. Proposed framework for feature subset selection.
the SU value for 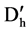
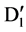
In this, we have given a High Dimensional dataset with M different attributes and a class label C, the approach finds a set of predominant attributes subset for the class values and reject all other attributes which are irrelevant. It can be divided in to two sections. In the earlier section, it calculates the 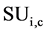
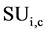
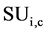
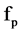
The process start with the calculation of SU for each attributes, after that we select the first and last element and continues as follow. Calculate the middle index of the sorted element and divide the whole attributes into two parts. In the first part, we start from the first element to the middle index and in the second part from last element till the middle index. For all the remaining feature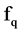
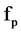
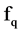
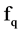
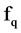
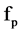
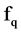
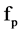
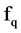
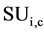
5. Computational Complexity of Proposed Approach
We analyze time complexity of the proposed algorithm. In the computation of symmetric uncertainty (SU) values of each feature have linear time complexity in terms of the number of feature M. Most of the time this number of feature also called dimensionality of datasets. Subsequently, this task is performed only once and stored in D’, the computation is consider negligible in compared to the further consideration of important features. In the second part (14 - 23) and (24 - 33), in each round, the proposed algorithm can delete a large number of attributes that are redundant to the fp in the same loop. In the best case, all of the remaining fq will be redundant and so all of attributes are removed and time complexity will be of order O(M)). In the worst case, when all the fq are stored in the D’ the time complexity will O(M2). In the average case, we can assume that out of important attribute half of the attributes are deleted in the each iteration. So, the time complexity may be of order O(M logM) where M is the number of attributes. We divide the D’ into two part and treat them individually. On average, Line (14 - 23) and (24 - 33) can be computed in O(M/2 logM/2). Since, in the line (1 - 7) we calculate a pair of attribute’s SU values in term of the number of instances N in the data, so the complete complexity of the above proposed algorithm O(N M logM).
6. Experimental Result and Discussion
In our experimental work, we experimentally evaluate the effectiveness of the proposed technique. The objective of our proposal is to evaluate the method in term of speed, number of selected attributes, and predictive accuracy for a particular classifier on selected feature. The algorithm compared against some already existing techniques: Information gain (IG), Chi Square, ReleifF and FCBF on the 5 benchmarking high dimension datasets. Because our approach finding less number of features as compared to information gain, chi square, FCBC and ReliefF, results in reduction of time for the resultant mining algorithm. A list of datasets used in our approach is listed in the table 1. This table contains 5 benchmarking High Dimensional datasets along with their characteristics, number of attribute, how many classes contained in the datasets. All of these datasets are taken from the UCI Repository [25] . A brief summary of datasets is described in Table 1.
For each dataset from the table 1 we will run our algorithm and note down the time required to run in table 2 and the number of selected features by the proposed algorithm table 4. We are also analyze the same from some traditional algorithm like ReliefF, information Gain, chi square, FCBF and record time required and number of selected feature for each algorithm in table 2 and table 3.
For the validation of our proposed algorithm we have tested the classification accuracy against to different classifier. Mainly, decision tree, SVM and NB classifier are used to check the classification accuracy with all 5 previous feature selection. Table 4 shows the accuracy by J48 classifier on our techniques and four traditional features selection on reduced dataset. The full data column represent the accuracy on whole data. Similarly, Table 5 and table 6 show the accuracy obtained by NB and SVM classifier respectively, while considering the four dataset obtained by four feature selection techniques and our technique. From tables 4-6, we can observed that our proposed methods works more accurately as compared to the given feature selection techniques, that was the main goal of this work. We get the better result in compare to IG, ReliefF, Chai Square, but similar to
Table 1. Dataset and their description.
Table 2. Time required (in ms) for relevent feature by different feature selection techniques and out proposed techniques.
Table 3. A comparision of number of selected feature through various techniques and our tech.
Table 4. Classification accuracy by J48 classifier.
Table 5. Classification accuracy by NB classifier.
Table 6. Classification accuracy by SVM classifier.
FCFS method in respect to classification accuracy. But when we talk about the time consumption, our approach outperform then all other methods.
7. Conclusion
In this paper, we have proposed an algorithm for feature subset selection for High Dimensional datasets. We are using correlation based feature ranking method, symmetric uncertainty (SU), which forms the basis of our approach. Our future plan is to extend this approach on very High Dimensional data (it is proposed that the current approach be explored on very High Dimensional data (i.e. ovarian dataset)). We have noticed that this algorithm generally works fine with numerical data; we can also try to extend this approach to working with mixed type of data (containing both nominal and categorical) without normalizing them in discrete values. This may also solve the problem of feature selection for High Dimensional data and biological datasets with millions of features using this approach. Since, for example the next generation sequencing techniques in biological analysis can produce data with several millions features in a single computation. Existing approaches make it hard to access data of this dimensionality, which creates the challenges of computational power, algorithm stability and accuracy of algorithm in parallel.
References
- Song, Q., Ni, J. and Wang, G. (2013) A Fast Clustering-Based Feature Subset Selection Algorithm for High-Dimen- sional Data. IEEE Transactions on Knowledge and Data Engineering, 25, 1-14. http://dx.doi.org/10.1109/TKDE.2011.181
- Ben-Bassat, M. (1982) Pattern Recognition and Reduction of Dimensionality. In: Krishnaiah, P.R. and Kanal, L.N., Eds., Handbook of Statistics-II, Vol. 1, North Holland, Amsterdam, 773-791. http://dx.doi.org/10.1016/S0169-7161(82)02038-0
- Mitra, P., Murthy, C.A. and Pal, S.K. (2002) Unsupervised Feature Selection Using Feature Similarity. IEEE Transaction on Pattern Analysis and Machine Intelligence, 24, 301-312. http://dx.doi.org/10.1109/34.990133
- Blum, A.L. and Langley, P. (1997) Selection of Relevant Features and Examples in Machine Learning. Artificial Intelligence, 97, 245-271. http://dx.doi.org/10.1016/S0004-3702(97)00063-5
- Kohavi, R. and John, G.H. (1997) Wrappers for Feature Subset Selection. Artificial Intelligence, 97, 273-324. http://dx.doi.org/10.1016/S0004-3702(97)00043-X
- John, G.H., Kohavi, R. and Pfleger, K. (1994) Irrelevant Feature and the Subset Selection Problem. Proceedings of 11th International Conference on Machine Learning, New Brunswick, 10-13 July 1994, 121-129.
- Chow, T.W.S. and Huang, D. (2005) Effective Feature Selection Scheme Using Mutual Information. Neurocomputing, 63, 325-343. http://dx.doi.org/10.1016/j.neucom.2004.01.194
- Kim, Y., Street, W. and Menczer, F. (2000) Feature Selection for Unsupervised Learning via Evolutionary Search. Proceedings of 6th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, Washington, D.C., August, 365-369.
- Dash, M., Choi, K., Scheuermann, P. and Liu, H. (2002) Feature Selection for Clustering a Filter Solution. Proceedings of Second International Conference on Data Mining, Florida, 19-22 November, 115-122.
- Liu, H. and Yu, L. (2005) Toward Integrating Feature Selection Algorithms for Classification and Clustering. IEEE Transactions on Knowledge and Data Engineering, 17, 491-502. http://dx.doi.org/10.1109/TKDE.2005.66
- Yang, Y. and Pederson, J.O. (1997) A Comparative Study on Feature Selection in Text Categorization. Proceedings of 14th International Conference on Machine Learning, Nashville, 8-12 July 1997, 412-420.
- Nigam, K., Mccallum, A.K., Thrun, S. and Mitchell, T. (2000) Text Classification from Labeled and Unlabeled Docu- ments Using EM. Journal of Machine Learning, 39, 103-134. http://dx.doi.org/10.1023/A:1007692713085
- Guldogan, E. and Gabbouj, M. (2008) Feature Selection for Content-Based Image Retrieval. Signal, Image and Video Processing, 2, 241-250. http://dx.doi.org/10.1007/s11760-007-0049-9
- Vasconcelos, M. and Vasconcelos, N. (2009) Natural Image Statistics and Low-Complexity Feature Selection. IEEE Transactions on Pattern Analysis and Machine Intelligence, 31, 228-244. http://dx.doi.org/10.1109/TPAMI.2008.77
- Oveisi, F., Oveisi, S., Efranian, A. and Patras, I. (2012) Tree-Structured Feature Extraction Using Mutual Information. IEEE Transactions on Neural Networks and Learning Systems, 23, 127-137. http://dx.doi.org/10.1109/TNNLS.2011.2178447
- Press, W.H., Flannery, B.P., Teukolsky, S.A. and Vetterling, W.T. (1988) Numerical Recipes in C. Cambridge Univer- sity Press, Cambridge.
- Ng, K.S. and Liu, H. (2000) Customer Retention via Data Mining. Artificial Intelligence Review, 14, 569-590. http://dx.doi.org/10.1023/A:1006676015154
- Liu, H. and Motoda, H. (2001) Feature Extraction, Construction and Selection: A Data Mining Perspective. Second Printing, Kluwer Academic, Boston.
- Ding, C. and Peng, H. (2003) Minimum Redundancy Feature Selection from Microarray Gene Expression Data. Proceedings of the IEEE Computer Society Conference on Bioinformatics, Berkeley, 11-14 August 2003, 523-528.
- Yu, L. and Liu, H. (2003) Feature Selection for High-Dimensional Data: A Fast Correlation-Based Filter Solution. 20th International Conference on Machine Learning (ICML-03), Washington DC, 21-24 August 2003, 856-863.
- Hariri, S., Yousif, M. and Qu, G. (2005) A New Dependency and Correlation Analysis for Features. IEEE Transactions on Knowledge and Data Engineering, 17, 1199-1207. http://dx.doi.org/10.1109/TKDE.2005.136
- Almuallim, H. and Dietterich, T.G. (1991) Learning with Many Irrelevant Features. Proceeding of 9th National Con- ference on Artificial Intelligence (AAAI-91), Anaheim, 14-19 July 1991, 547-552.
- Kononenko, I. (1994) Estimating Attributes: Analysis and Extensions of RELIEF. Machine Learning: ECML-94, Euro- pean Conference on Machine Learning, Secaucus, 6-8 April 1994, 171-182.
- Kannan, S.S. and Ramraj N. (2010) A Novel Hybrid Feature Selection via Symmetrical Uncertainty Ranking Based Local Memetic Search Algorithm. Knowledge-Based Systems, 23, 580-585. http://dx.doi.org/10.1016/j.knosys.2010.03.016
- Blake, C.L. and Merz, C.J. (2010) UCI Repository of Machine Learning Database. Department of Information and Computer Sciences, University of California, Irvine.