Open Journal of Modelling and Simulation
Vol.05 No.03(2017), Article ID:77788,8 pages
10.4236/ojmsi.2017.53013
Simulation Analysis of Flow Characteristics in the Vortex Diode with Double Tangential Tube
Lijun Zhang, Yuelai Dai, Yulei Li, Qun Wang, Xiaoyu Jin, Lan Ma, Wentao Huang
Ningbo Sub-Academy, National Weapons Science Research Academy, Ningbo, China

Copyright © 2017 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution-NonCommercial International License (CC BY-NC 4.0).
http://creativecommons.org/licenses/by-nc/4.0/



Received: April 29, 2017; Accepted: July 18, 2017; Published: July 21, 2017
ABSTRACT
The paper analyzed flow characteristics in vortex diode with double tangential tube by numerical simulation. Compared to traditional vortex diode with one tangential tube, the structure of double tangential tube can reduce the forward resistance and improve overall performance. The symmetrical design adopted in vortex diode with double tangential tube; the internal flow field in chamber showed symmetrical distribution in the reverse flow, which can improve the flow stability and accelerate the convergence speed in simulation.
Keywords:
Vortex Diode, Double Tangential Tube, Performance Parameters

1. Introduction
As a new maintenance-free device, vortex diode pump device begins to be used in nuclear industry for spent fuel transportation, and is extended to the chemical and pharmaceutical industries. The basic working principle of vortex diode is that its working fluid through the pros and cons vortex diode has different drag coefficients, which is similar to the role of “diode” in the circuit. The structure of Vortex diode includes three parts: tangential tube, axial tube and chamber. In the case of forward flow, the working fluid flows into the chamber from the axial tube, and outflows from the tangential tube. Its internal flow field is relatively simple. In the case of reverse flow, the working fluid flows into the chamber from tangential tube and outflows from the axial tube. The internal field is rendered as complex three-dimensional turbulent flow field, in which a strong vortex is formed near the center of chamber. The most important parameter to measure its overall performance is impedance ratio which is defined as the ratio of reverse resistance coefficient to the forward resistance coefficient.
Many scholars have done a lot of work in studying the structure of vortex diode. Tapered and divergent structure was used in the axial tube. Taper angle of tangential tube was changed and the chamber in configuration was designed. All above is in order to improve its overall performance or one-way performance. In addition, some calculation models were considered in reverse flow. Malhotra A used standard k-ε model to calculate swirl problem, which had a degree of error [1] . Realizable k-ε model and RNG k-ε model were used by Speziale C G to calculate turbulence model for separated flows; the results were better than standard k-ε model, but not ideal [2] . Reynolds stress model was very close to the experimental results, verified by Launder B E [3] . Large eddy simulation is the best model in swirl flow, verified by Pierce C D, but quite time-consuming [4] . In overall consideration, Reynolds stress model is suitable to calculate swirl problem. However, less research is done on vortex diode with double tangential tube.
This paper analyzed flow characteristics in vortex diode with double tangential tube by numerical simulation. Vortex diode with double tangential tube shows better performance in the forward flow and overall performance, compared with traditional vortex diode. What’s more, the convergence performance is improved, which can reduce computing time.
2. Working Mechanism and Characteristic Parameters
The traditional vortex diode structure is shown in Figure 1, whose working mechanism is as follows. When the fluid flows from the tangential tube into the axial tube, the working fluid jets into the chamber due to the contraction of the pipe, so that a vortex is formed by the action of the wall. This leads to a great flow resistance, which is called reverse flow. When the working fluid flows from the axial tube into the tangential tube, the flow, known as the forward flow, is relatively simple. In this condition, no swirl flow is generated so that the flow resistance is relatively small. The main performance parameters of vortex diode include the resistance coefficient ξ (Euler number Eu) and the impedance ratio ε:
 (1)
(1)
Figure 1. The 3D model of vortex diode.
 (2)
(2)
where ∆P is the difference between input pressure and output pressure and ρ is the density of working fluid. u is the velocity of working fluid. EuF is the forward flow resistance coefficient and EuR is the reverse flow resistance coefficient.
3. The Model
3.1. Geometry Model
The vortex diode structure of double tangential tube is shown in Figure 2. The structure of the two tangential tubes set symmetrically are the same. Cavity diameter of chamber is 150 mm, and the tube diameter of import and export are both 25 mm. Pre-treatment of finite model is carried out by ICEM software. Hybrid meshes are generated using structured grids and unstructured grids, and tetrahedral meshes are applied to joints between chamber and tangential tube. The rest part is meshed by hexahedral meshes. Mesh quality is good, and the total number of grids is more than 80 million.
3.2. Calculation Model
In Forward flow, for it is in isotropic turbulence state, so the calculation model uses the standard k-epsilon model. In reverse flow, the fluid inside the chamber presents vortex motion, which shows the performance of anisotropy and instability. For the swirl problem, standard k-ε model, realizable k-ε model, RNG k-ε model, Reynolds stress model and large eddy simulation model can all be considered. Although realizable k-ε model and RNG k-ε model are more reliable than standard k-ε model, they are still not ideal. Reynolds stress model directly models individual items, which is better than the two models above in simulation results. Large eddy simulation has the best performance, but it is time-consuming during computation. Given simulation accuracy and economy, Reynolds stress model is appropriate to be used to calculate in reverse flow.
3.3. Boundary Conditions and Solution Control
The import condition of forward and reverse flow are set as speed of working
Figure 2. The 3D model of vortex diode with double tangential tube.
fluid. Outlet pressure is set as the constant 0, while a given hydraulic diameter and turbulence intensity are taken as import turbulent conditions. In reverse
flow simulation, import Reynolds stress values meet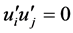 ,
, 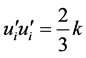 , and export Reynolds stress values satisfy
, and export Reynolds stress values satisfy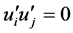 ,
, 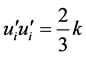 [5] . Due to a long pe-
[5] . Due to a long pe-
riod of swirl at the outlet, the outlet pressure produces reflux phenomenon, so the outlet boundary condition is set as outlet-vent and reflux is eliminated by increasing the resistance loss coefficient at the outlet. Equations are solved in Fluent, and the reference pressure (Pressure-Based) algorithm is adopted. In addition, optimization polyhedron tetrahedral mesh grid technology is applied, and PRESTO is used to discrete items of pressure as well. The SIMPLE algorithm is applied to format, pressure and velocity coupling, and second order upwind scheme is applied to Momentum and turbulence kinetic energy dissipation rate too [6] . Fluid field are considered as steady flow, and temperature influence is ignored. Working media is water for simulation. Convergence criteria is that importers mass flow flux difference ratio is less than 10−5.
4. Numerical Results
4.1. Contrast of Performance Parameters
Figure 3 and Figure 4 show that the forward and reverse resistance coefficient of vortex diode with double tangential tube are both reduced compared to the traditional vortex diode, so is its impedance ratio. In other words, its overall performance is improved.
4.2. Internal Flow Field Analysis
The pressure and speed contours of the vortex diode with double tangential tube are shown in Figure 5 and Figure 6. When import velocity of two tangential tubes is 5 m/s, both tangential tubes show symmetric distribution in pressure and speed, so the internal flow field is stable. The import and export pressure are obviously different, and the maximum velocity is near the center of the chamber because of the rotation. Figure 7 shows that a vortex structure of velocity vector is formed in the central position.
Figure 3. Forward and reverse resistance coefficient of the two different structures.
Figure 4. Impedance ratio of the two different structures.
Figure 5. Contours of static pressure.
Figure 6. Contour of velocity.
Figure 7. Vector of velocity in the chamber.
4.3. Contrast of Reverse Flow Simulation Time
Due to the stability of the internal flow field, the convergence speed has improved significantly in reverse flow. Figure 8 shows the computation time of two
Figure 8. Computation time of two different structures in the same computer.
different structures in the same computer.
5. Conclusion
At the same Reynolds number, impedance ratio of the vortex diode with double tangential tube is significantly higher than ordinary vortex diode. With one more exit tube set than ordinary vortex diode, forward flow resistance decreases significantly, and the reverse flow resistance reduces at the same time. Thus, the comprehensive performance is improved. Due to the symmetry of the structure, the internal flow field of reverse flow exhibits symmetrically, which improves the flow stability and speeds up the computing rate significantly as well. Multi-tube vortex diode structure can provide reference for improving the performance of vortex diode.
Acknowledgements
Sincere thanks to the members of OJMSi for their professional performance and high quality work.
Cite this paper
Zhang, L.J., Dai, Y.L., Li, Y.L., Wang, Q., Jin, X.Y., Ma, L. and Huang, W.T. (2017) Simulation Analysis of Flow Characteristics in the Vortex Diode with Double Tangential Tube. Open Journal of Modelling and Simulation, 5, 174-181. https://doi.org/10.4236/ojmsi.2017.53013
References
- 1. Malhotra, A., Branion, R.M.R. and Hauptmann, E.G. (1994) Modelling the Flow in a Hydrocyclone. The Canadian Journal of Chemical Engineering, 72, 953-960.
https://doi.org/10.1002/cjce.5450720603 - 2. Speziale, C.G. and Thangam, S. (1992) Analysis of an RNG Based Turbulence Model for Separated Flows. International Journal Engineering Science, 30, 1379-1388.
https://doi.org/10.1016/0020-7225(92)90148-A - 3. Launder, B., Reece, G.J. and Rodi, W. (1975) Progress in the Development of a Reynolds Stress Turbulence Closure. Journal of Fluid Mechanics, 68, 537-566.
https://doi.org/10.1017/S0022112075001814 - 4. Pierce, C.D. and Moin, P. (1998) Large Eddy Simulation of a Confined Coaxial Jet with Swirl and Heat Release. Proceedings of the 29th AIAA Fluid Dynamics Conference, Albuquerque, NM, 15-18 June 1998, AIAA 98-2892.
https://doi.org/10.2514/6.1998-2892 - 5. Jordan, K., Zahrai, S., Macchion, O. and Vomhoff, H. (2006) Numerical Modeling of Highly Swirling Flows in a Through-flow Cylindrical Hydrocyclone. AIChE Journal, 52, 3334-3344.
https://doi.org/10.1002/aic.10955 - 6. Kulkarni, A.A., Ranade, V.V., Rajeev, R. and Koganti, S.B. (2008) CFD Simulation of Flow in Vortex Diodes. AIChE Journal, 54, 1139-1152.
https://doi.org/10.1002/aic.11439









