ABSTRACT

The behavior of Li warm plasma (i.e. T in 1 eV range) is reported for a range of temperatures (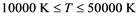) and densities (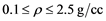), spanning moderate to dense conditions. Quantum Molecular Dynamics (QMD), in Carr-Parinello approach, is used to advance and equilibrate an ensemble of 54 Li atoms at desired temperature and density. The charge distribution and ions positions are further input in a DFT finite temperature calculation, producing, self consistently, a large number of energy levels (300 - 1500) and occupation numbers, from which real and imaginary parts of the dielectric function are obtained. Optical quantities like index of refraction, reflectivity, absorption coefficients and Rosseland means are deduced. Zero frequency static conductivity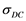, diffusion coefficients and a Hugoniot curve are calculated.

Keywords:

QMD, FTDFT, Opacity, Rosseland

1. Introduction

Gas discharge is often used in plasma investigations. The densities achieved run from 10¹⁴ electrons/cc for a conventional setup up to 10¹⁸ for more intricate techniques, like capillary gas discharge. In tokomaks the density is also at the 10¹⁴ mark. In our sun, a giant plasma laboratory, there are a variety of densities, 10⁵ in solar corona, 10⁸ in chromosphere, 10¹⁵ in photosphere etc. Plasma studies hence, were traditionally concerned with low densities environments, very much below the nominal solid density at 10²³.

With the advent of new facilities and techniques, like inertial confinement fusion (ICF), National Ignition Facility at LLNL, high energy density physics experiments, shock experiments etc., the interest is shifting toward a regime of warm dense matter (WMD). Warm means temperatures in the range 10³ - 10⁶ K, but typically near 10,000 K (1 eV), while dense encompass a range from a fraction of STP density 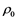(~10²¹ atoms/cc), to many times 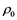(~10²⁵ atoms/ cc). In this regime the plasma is populated by free electrons, ions (positive or negative), atoms, molecules if the chemistry permits it, or aggregates of two or more ions: dimmers, trimmers, etc. All these populations are very dynamic, evolving all the time, due to mutual interactions through collisions, ionization, recombination, chemical reactions and so forth.

To model such an environment a most appropriate tool is the molecular dynamics (MD) in which the atoms (ions) are followed individually through their interactions and trajectory in space, time and energy. In classical MD the ions interact through an empirical potential fixed in time (the electrons play no role), therefore the dynamicity of the system is not fully accounted. Contrary, in quantum molecular dynamics (QMD) the electrons are given an equal role with the ions, and even more, they are treated fully quantum mechanically in the framework of density functional theory (DFT). The fixed potential is no longer needed and the interactions are described realistically depending on time and space. The QMD is obviously the tool of choice but comes at a price, only small ensembles of atoms and relatively short times can be simulated.

Planetary interiors are studied in the WMD regime [1] [2] and also white dwarfs, where average densities are 10⁶ g/cc and the effective temperature, deduced from luminosity, is in the range 8000 - 16,000 K for most of them [3] . White dwarfs have very low remnants of He (≤1%) and H (≤0.01%) which form a thin and very opaque atmosphere, hence there is interest in their optical properties (index of refraction, reflectivity, absorption coefficient) which are significant for the radiation transport.

Electric conductivity, dielectric function and all the other optical properties can be obtained within finite temperature density functional theory (FTDFT), as formulated by Mermin [4] , using the ions configurations generated in a QMD calculation coupled with the Kubo-Greenwood (KG) [5] [6] formula. This three steps approach, QMD + FTDFT + KG, was used in the last 10 - 15 years for a number of calculations, mainly on Hydrogen and Deuterium [7] [8] [9] , relevant for stellar interiors and atmospheres as well as for ICF pellets, but also on Aluminium [10] [11] , Sodium [12] and Iron [13] , relevant for planetary interiors, particularly Earth.

Large astrophysical data bases, like OPAL, containing opacities (i.e. absorption coefficients) and their Rosseland means, concentrate on a number of elements defined as belonging to stellar, or more precisely, to solar atmosphere. Lithium is not included in the solar composition and has not received to much attention regarding its optical properties.

Nevertheless, Lithium, which is considered a simple metal, is slightly more complex than H, D, and He and it is worthwhile to investigate it in the frame- work of the above formalism. Indeed a recent paper [14] reported results for densities in the range 0.1 - 10 g/cc and temperatures of several hundred up to 10,000 K.

The goal of the present work is to extend Lithium investigation to a higher temperature range from 10,000 K to 50,000 K, while maintaining realistic den- sities close to those of the solid. This region lacks proper experimental data and will be of interest in stellar scenarios different from our sun.

2. Theoretical Formalism

The response of a medium to an electromagnetic wave (like light) is charac- terized by its dielectric function. The optical properties are derived from the frequency dependent, long wavelength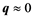, complex dielectric function:

(1)

The real 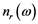and imaginary 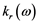parts of the index of refraction are [15] :

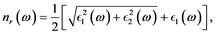(2)

(3)

which together are giving the reflectivity:

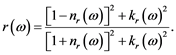(4)

The following relations are useful:

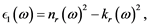(5)

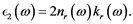(6)

The dielectric function will be actually computed (see Section 3.3) from the complex conductivity: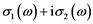

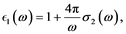(7)

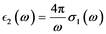(8)

The imaginary part of conductivity is related to the real part of dielectric function and vice versa.

The absorption coefficient is [16] :

(9)

and with the help of Planck distribution:

(10)

the Rosseland mean opacity is obtained as [17] :

(11)

where the absorption coefficient is dependent both on the temperature T and the density.

Perrot [16] defines a true absorption coefficient in dielectric material as:

(12)

and argues that the Rosseland mean opacity expression should be modified as:

(13)

The integrations above extend to but the weighting function is quite strongly peaked at and asymmetric (a longer tail toward lower energies and an abrupt drop at higher energies). Therefore reasonable results for can be obtained with only a finite range calculation of.

The Planck mean, can be calculated in a similar way:

(14)

or with Perrot [16] true absorption coefficient:

(15)

3. Calculation of the Dielectric Function

The calculation proceeds in three steps by a procedure well established in the literature: Mazevet et al. [10] , Silvestrelli [11] , Desjarlais et al. [9] .

First, an ensemble of Li atoms is equilibrated, at desired density and tem- perature, by a QMD calculation. When the system is stable, the QMD run is sampled a number of times. The sampled configurations, consisting of ions coordinates and total charge distribution, serves as input to a second finite temperature density functional (FTDFT) step. In this step a large number of energy levels, occupation numbers and respective Kohn-Sham electron wave- functions are calculated self consistently (SCF). These last products are the key ingredients, in a final step, for calculating the real conductivity by Kubo [5] and Greenwood [6] formula. is obtained by a Kramers-Kröning principal part integration and the dielectric function from 7 and 8.

The first two steps were calculated with the Quantum ESPRESSO [18] software system cp.x and pw.x programs. For the third step a modified form of the epsilon.x program of Quantum ESPRESO was implemented.

3.1. The QMD Step

An ultrasoft pseudopotential for Li, taken from Vanderbilt uspp-7.3.4 code distribution [19] , was chosen for the QMD calculation. The potential, for one valence electron, was tested for convergence to the experimental lattice parameter of bcc Li of 3.49 Å, Figure 1.

The found minimum is 3.56 Å. The cutoff energy chosen for subsequent QMD was 20 Ry, which gives a minimum of only ≈ 2 mRy above the best

minimum at a cutoff of 60 Ry.

As is customary in QMD only the G k point of the Brillouin zone is sampled. A time step of 4 AU (≈0.1 fs) was used, implying 10,000 steps/ps. The initial configuration of 54 Li atoms, at a given density in a simple cubic cell, was generated with the PACKMOL [20] program, disregarding any symmetry. Periodicity in all 3 dimensions is assumed. The system was brought to ground state and relaxed to eliminate too strong force components. The system was advanced in time in NVT (canonical ensemble) mode with Nosé thermostats on both ions and electrons, kept at equal temperatures (i.e. thermal equilibrium is assumed). This scheme does not keep strictly constant neither the temperature or the total physical energy. These quantities are kept constant only on an average sense. The only strictly conserved quantity is an “energy”, peculiar to the Car-Parrinello extended Lagrangian [21] [22] , which includes, besides the physical energies, also terms depending on the fictitious masses used by the thermostats. An example of a QMD run history is shown in Figure 2. Block averages (to eliminate correlations) of these data show that the physical energy is constant in 0.2%, the temperature in 2.5%, while the CP energy in 0.0025% ().

For the lowest density included in the calculations and tem- peratures and also for and the number of atoms was lowered to 16. The calculated radial distributions, for all the densities and temperatures of the present study, are essentially featureless, see Figure 3, lacking any trace of a solid long range or even liquid short range order. This behavior is consistent with a zero translational order parameter, Figure 4.

Other quantities of interest produced by a QMD simulation are the velocity

autocorrelation function, the mean square displacement, Figure 5, from which the diffusion coefficient can be obtained either by Einstein relation or by a Green-Kubo relation [24] , and the pressure at a given density and temperature, Figure 6. From pressures, densities and temperatures, a numerical equation of

state (EOS) can be constructed (for the limited range of simulations) by a method given by Lenosky et al. [8] .

3.2. The FTDFT Step

In the last 1 ps of the QMD run a snapshot of the system was taken at every 2000 steps (0.2 ps), 5 snapshots in all. The purpose is to average over the results from the different snapshots. These snapshots include ions positions, electric charge distribution, Kohn-Sham electrons wavefunctions (i.e. their expansion in plane waves) and other miscellaneous information regarding inverse lattice G vectors, their stars, etc. This information was fed into the pw.x (PWscf-plane waves self consistent field) program of Quantum ESSPRESO. Actually only the ions positions (which will be kept fixed) and the electric charge distribution were needed. In this step a PAW (Projector Augmented Wave) pseudopotential of Blöchl type [25] was employed. The change in pseudopotential is necessary due to difficulties in calculating dipole matrix elements with ultrasoft pseudo- potentials, see next section discussion.

The actual PWA pseudopotential was constructed with the atompaw program of Holzwarth at al. [26] . The input was taken directly from their examples with a slight modification of adding a 4-th basis function, enabling decent fits to the logarithmic derivatives, Figure 7 (all the electrons were considered to be valence electrons, no core). The exchange-correlation functional is of PBE type [27] , and the electronic calculation is done in the Generalized Gradient Approximation (GGA). The same approximation is used further in the scf calculations done with pw.x.

An analysis similar to Figure 1 yields, for the PAW pseudpotential, an equilibrium bbc Li lattice parameter of 3.46 Å (closer to the experimental 3.49 Å

compared with the uspp result) and a cutoff of.

The finite temperature density functional calculation, in the sense of Mermin [4] , is realized in PWscf by imposing a Fermi-Dirac smearing of width on the occupation numbers of the electrons [18] . The goal was to calculate an enough number of states such that the minimum occupation number is. The calculation was done self consistently for a number of 300 levels. If the goal was not archived within this number of levels, it was proceeded further, non consistently, for an additional number of levels until the threshold of minimum occupation number was reached. The goal was easily reached for high densities but difficult for low densities and high temperatures. For example at and, 1200 levels are necessary to reach a minimum occupation of. The problem of achievable minimum occupation, imposed a reduction in the number of simulated atoms, from 54 to 16, at the lowest calculated density and temperatures. An example is shown in Figure 8.

The density of states, Figure 9, shows a high and localized peak of the two 1s electrons, and a loose structure, below and above the Fermi energy, coming from the 2s (with some 2p mixture) electrons.

3.3. Conductivity Calculation

Following Harrison [28] , the current in a metal is assumed to be of the form

(16)

with the electric field.

A calculation of the expectation value of, in first order perturbation theory, using density matrices based on the Kohn-Sham electron wavefunctions, and an interaction Hamiltonian between the electrons and the field of the form

, yields the Kubo-Greenwood formula [5] [6] for (Harrison [28] p. 320).

In the notation of [13] [15] , with atomic units (), for a par- ticular k in BZ:

(17)

with the energy of the light photon, the volume of the simulation cell and the Fermi-Dirac occupation number of the i-th Kohn-Sham state of energy. are the matrix elements of the electromagnetic field, in the dipole approximation, between the Kohn-Sham i and j states. The square is averaged over the three spatial directions:

(18)

The operator above is the real space representation of the operator, appearing in the dipole approximation of the electromagnetic field. The use of the real space representation is permitted with local potentials. In general pseudopotentials of the Troulier-Martin type, or especially ultrasoft pseudopoten- tials are non local. In this case one should use the anticomutator [29] [30] , with the total Hamiltonian. Expressions for the matrix elements, in the case of nonlocal potentials, were given by Gonze [31] . They are involved and difficult to implement.

The PAW potential is an all-electron local potential and the Equation (18) is valid [30] . For this reason the majority of previous works preferred to use a PAW potential.

The FTDFT step 2 produces a pseudo-wavefunction from which, in PAW method, the full wavefunction can be recovered [30] . Only recently a formalism for calculating the matrix elements with the full wavefunction was developed [30] .

In the present work the matrix elements are approximated by calculating with the pseudo-wavefunction:

(19)

where is a reciprocal lattice vector and is the complex coefficient of the plane wave in the expansion of.

The function in Equation (17) is implemented as a Lorentzian:

(20)

the broadening parameter was optimized to damp oscillations due to gaps in the states energies but not to wipe features in.

The BZ is sampled at a number of special k points chosen from Monkhorst- Pack [32] sets without symmetries, i.e. all the k points have equal weights. The final conductivity is:

(21)

with the total number of k points in set.

Figure 10 presents some details of calculation. From Equation (7)

and Equation (8) it is obvious that the natural units of conductivity are units of frequency. Indeed some older papers show conductivity in sec⁻¹. More recent papers prefer to quote the conductivity in units of inverse resistivity, namely [Ohm・cm]⁻¹. Figure 10 follows this convention. Panel 1) shows the full calculated at and and averaged over the 5 snap- shots taken from the QMD. The range of photon energies covered (~100 eV) is based on the range of energies appearing in the DOS Figure 9. The bump around 60 eV is clearly due to transitions from the deep 1s states to the states in vicinity of the Fermi energy. The presents some distortions at very low energies and some oscillations which the chosen value of did not smooth them out completely. For obtaining the DC conductivity at a 4-th order polynomial fit is done and shown in panel 2). The range of the fit is but only is shown. The dispersion of values from the individual snapshots calculations is presented in panel 3). There are quite visible differences at low energies. At higher energies they almost disappear. The sampling of the BZ was tested with a number of Monkhorst-Pack [32] (MP) special points sets: (2 1 1)-2 k points, (2 2 1)-4 k points and (2 2 2)-8 k points. The dispersion in the resulting is shown in panel 4), for a single snapshot. Only at low energies differences are observed. They don’t seam to be larger than the ones observed between different snapshots. The mini- mal MP set (2 1 1) of 2 k points was used for all the production runs.

The calculated should fulfill the sum rule [13] :

(22)

with the number of electrons in the simulation cell ().being calculated only in a finite range of, depending on the number of cal- culated Kohn-Sham states, some deviations from the sum rule are expected.

The sum rule was fulfilled at 90% - 96% level at higher densities (where a low number of levels is sufficient to reach very low occupation numbers) and worse at lower densities where very large number of levels are needed.

The imaginary part is obtained from the principal value integral [15] :

(23)

Some other quantities of interest obtained from the calculations in this section are presented in Figure 11. The Electron Energy Loss Spectrum (EELS) is defined from the dielectric function as:

(24)

the plasmon peak is apparent.

The absorption coefficient can be compared with one given in [15] for LiH at. Both peak somewhere around 10 eV. The additional feature beginning at 40 eV, in Figure 11, is just the K edge of the 1 s electrons in Li, smeared by the temperature. The binding energy of the 1 s electrons, from an all electron calculation, is 51.8 eV. is quite similar with because it characterize the extinction (i.e. absorption) of light.

4. Results and Discussion

4.1. EOS

The relation of the three thermodynamic quantities forms an Equation of State (EOS). It is valuable in various fields of science, like, for example, planetary and stellar physics, in which strong compression and high tempera- tures are present.

The QMD calculations of stage 1 were performed at 36 pairs pro- ducing the pressure P as a function of and T. More information is produced, as discussed in Section 3.1, and in particular the total energy of the system. Using this information a smooth EOS can be produced, valid in the range covered by the QMD calculations.

Following Lenosky et al. [8] an internal energy per atom is defined as:

(25)

where N―the number of atoms in simulation,―the total energy of the system obtained in the QMD calculation, and―the Boltzman constant. A parametrized EOS is defined by two smooth polynomial functions for the pressure P in GPa, and the internal energy per atom in Ha:

(26)

(27)

where is the density expressed as number of atoms per unit volume (in, i.e. AU), and the temperature T in K. The powers of T considered are −2 - 1 (4 values) and those of n from 0 to 4 (5 values). The number of parameters is thus very large (40), more than the number of pairs calculated. In [8] a particular (i.e. specific ij pairs) restricted set of 7 c_ij and 10 d_ij was considered for deuterium. They were chosen based on physical considerations. In the present work the same set was adopted as it is. No attempt was made to change the number of parameters or the specific ij pairs.

The two Equations (26), (27) apparently can be fitted independently. There- fore an additional well known thermodynamic condition, providing a link between the two equations, is imposed as a constrain:

(28)

The right side is in and should be multiplied by to bring it to GPa. The left side is calculated only with the parameters while the right side only with. Equating the coefficients of, on both sides, a relation between and is obtained:

(29)

or conversely:

(30)

The numerical factors take care of units. An inspection of Table 1 and Table 2 reveal the presence of six couples c_ij-d_i-1j in the restricted set, hence reducing the number of independent coefficients from 17 to 11. The particular couple c₁₁-d₀₁ is problematic, in both Equations (29) or (30) an indefinite 0/0 indices ratio is present. Hence, because the thermodynamic constrain is not actually fixing the relation between these two parameters, they were left both free, rising the number of fitted parameters to 12.

The thermodynamic constrain was implemented as a penalty function (PF) added to the:

(31)

where and are the left and right hand sides of Equation (28); is the number of evaluations (=90, 9 values of T and 10 values of n, in the range of QMD calculations) .

At the end of the fit, therefore the constrain is well obeyed. The

average discrepancy in P is 5% (with 5 points and a maximum of 21%), and in U 2% with a maximum of 8%. Figure 12 shows the calculated QMD P points, as a function of T and ρ compared with the EOS fit. Small discrepancies are observed at low densities and temperatures. The biggest one, 21%, is at and.

The fitted parameters are presented in Table 1 and Table 2.

4.1.1. Isotherms

The EOS is studied experimentally in compression experiments such as modern diamond anvil cell techniques plus X-ray diffraction or older piston cylinder apparata. In these type of experiments the temperature T is constant, usually the room temperature, producing isotherms. The lowest isotherm in the present calculations is. Figure 13 shows experimental data (up to 21 GPa), a theoretical isotherm at, and our isotherm at.

Boettger and Trickey (BT) [35] calculated, by a LMTO technique, a theoretical cold EOS, without a T dependence. It made its way as the cold part of EOS 2293 [36] in the SESAME [37] database. Their cold EOS fits nicely the experimental points in Figure 13. It can be seen that the 10,000 K isotherm is less stiff (lower slope) at high densities (lower volumes). This trend continues in Figure 12 with lower and lower slopes at higher temperatures.

4.1.2. Hugoniot

Another technique to study EOS is by shock experiments. In these experiments, starting from an initial state, a final state is attained, in which all three thermodynamic quantities are changed. The Hugoniot curve is the locus of states of pressure P, volume V (or density ρ) and internal energy U,

which can be attained by applying different shock intensities, when starting from the same initial conditions. Noting by, and the quantities behind the shock front and by, and the initial conditions, the Hugoniot equation [38] is:

(32)

What is actually measured are two velocities: -shock velocity and - particles velocity, related to other quantities by [39] :

(33)

(34)

In Equation (32) apparently there is no explicit dependence on temperature but an EOS is an absolutely prerequisite for solving it (one needs 3 equations for 3 unknowns).

The chosen initial conditions where Ha/atom, based on a QMD run at 300 K, and, the STP density of Li. The left hand side of Equation (32) was minimized with MINUIT [40] at a fixed [the part should be multiplied by to get it in as the part] resulting in a value for. was sampled on a very fine mesh (1000 K steps) from 10,000 K to 50,000 K, the region where the EOS is valid. The solution was accepted if the minimum in the objective function was. The set of values, together with the derivated quantities define the Hugoniot curve, Figure 14.

Data from the LASL shock dat a library [42] are below the range of the calculated Hugoniot. Data of Bakanova et al. [43] have some overlap with the calculated range, but was criticized in [41] as being too soft (i.e. predicting too low pressures with increasing density) and probably in error. It is definitely below the calculated Hugoniot. The Hugoniot curve of Young and Ross [41] is based on only 4 points given in their paper, hence its fractured appearance. The large discrepancy between their curve and ours is, in part, due to lack of points between their last value at, and one before last at,.

Our values close to these V points are 194 GPa and 92 GPa, respectively, so while at the two curves agree rather well at Young and Ross’ Hugoniot climbs almost twice as fast becoming very stiff. Regarding vs, one can discern a change in the slope in respect with the experimental data [39] [42] . This is in agreement with a general feature of Hugoniot in metals, as was proposed by Johnson [44] , were a change in slope is always present near.

Numerical data for the calculated Hugoniot curve are presented in Table 3.

4.2. Sylvian Kahane

DC conductivity and Diffusion coefficient D

The DC conductivity is the static limit of. This quantity can be measured experimentally. In calculations it was obtained by a polynomial fit to

, in the range, as shown in Figure 10. Its dependence on density is shown in Figure 15 and compared with results from Kietzmann et al. [14] at lower temperatures.

Kietzmann’s decreases with increasing density in the region 0.53 - 3 g/cc, but increases with the density outside it, forming a region of inversion. This is considered typical of metals. No region of inversion is observed in Figure 15, except perhaps a hint of it at. For higher temperatures the conductivity increases all the way in the range of considered.

In the work of Desjarlais, Kress and Collins [9] on Al, an inversion region in the range 0.01 - 0.1 g/cc is seen at lower T, but it is wiped out at. Li behaves, thus, similarly. Moreover, Kietzmann et al. identified the inversion region being a fluid metal, where the ion-ion pair correlation function shows short range order typical of liquids. Not such order is seen in Figure 3 at higher temperatures.

Bastea and Bastea [45] and Fortov et al. [46] measured the conductivity in Li. Both works used the quasi-isoentropic technique in which a shock wave is traveling back and forth in the sample, reflected by the anvils (saphire or steel), increasing the pressure. In [45] the reported temperatures varied from 2000 K to 7000 K and P reached 180 GPa, while in [46] T was lower than 3000 K and P reached 210 GPa, thus both are below the present calculations range of T.

The conductivity and other quantities dependence on temperature is shown in Table 4.

The values of the diffusion coefficient D are very well reproduced by an Arhenius function only for. At 10,000 K the calculated D is substantially larger than Arhenius fit. The values of

are 4.33 and 2.82 eV for and 1.5 g/cc respectively, with and 0.177 cm²/s.

The reduced diffusion coefficient is defined as with ―the ions plasma frequency,―Wigner-Seitz radius,―the ions number density,―atomic mass, and―the average ionization = 1 at the calculation temperatures. Its values are one order of magni- tude larger compared with the one component plasma fit given by Hansen et al. [47] .

4.3. Rosseland Mean Opacity

The absorption coefficient is sometimes called opacity, in particular in the Astronomy and Astrophysics (A&A) field, which is concerned with radiation transport through stellar envelopes. The Rosseland mean opacity is a harmonic i.e. of) weighted mean, depending on and, conveniently giving a single number figure of merit for the radiation transport. It was calculated with Equation (11).

Some of the present results are compared in Figure 16 with results based on opacities calculated with the atomic modeled plasma by collisional-radiative FLYCHK code [48] .

In the atomic model the attenuation of radiation involves electron transitions (bound-bound, bound-free, free-free) in an isolated atom. It is appropriate, hence, mainly for diluted plasmas or gases. When the density is larger the interaction between neighboring atoms begins to come into play. If this density effect is still weak, it can be treated as a perturbation in the framework of the atomic model, but when the density is large and the atoms close, the isolated model will fail and a more collective approach is needed. The QMD + FTDFT

offers such alternative model, in which the interaction with the neighbors is built-in in the QMD step, while the electrons wavefunctions (needed for the transitions calculations) are obtained in the FTDFT step from a collective model, not resembling at all the isolated atom. The versatility of the QMD is illustrated in Figure 17 which shows the Li atoms at some position in time when 4 out of the 54 atoms clearly formed two Li₂ dimmers in which they are very close and, hence, the electronic wavefunctions are severely distorted by the presence of the neighbor atom.

Figure 16 shows that the QMD + FTDFT Rosseland mean opacities vary much slower compared with the corresponding atomic ones. This is in qualitative agreement with the results for hydrogen from [50] . To understand more on the differences between the present and atomic approaches one has to look at the absorption coefficients in Figure 18.

There is a sharp contrast below ~3 - 4 eV (the plasma frequency for the re- spective and is), where the QMD + FTDFT stops growing as, reverses course and declines slightly. This behavior is dictated by the conductivity (see Equation (9)) which approaches, quite flatly Figure 10), the zero-frequency limit, while the index of refraction varies only by one order of magnitude (Figure 11). On the other hand the atomic climbs higher and higher as approaches zero (this behavior is due to the free-free transitions), i.e. when the photon has very little energy and is not able to induce any electronic transition, the medium is totally opaque. The QMD + FTDFT prediction that for a photon of vanishing energy () the plasma is slightly more transparent than for a photon of 3 eV (Figure 18) is not so clear. This kind of behavior was received consistently in other works also [10] [50] . The plasma is permanently ionized at these tem- peratures (average 1⁺) so a low energy photon does not have to actually excite a

bound electron to induce a transition, so one can expect some flat opacity at low energies below.

The K-edge of the FLYCHK presents some strong oscillations due to the bound-bound transitions, but afterwards declines exponentially as expected. The QMD + FTDFT K-edge is shifted toward lower energies, reaches the same values as the atomic one and begins to decay exponentially. At 80 - 90 eV drops sharply due to the finite number of states calculated in the FTDFT step.

Neither the order of magnitudes differences in the absorption coefficient at low energies, or the differences at the K-edge, are really influencing the QMD + FTDFT vs. FLYCHK Rosseland means. As can be seen in Figure 18 the weighting function samples mainly in a small range around.

4.4. Experimental Optical Data

Experimental optical data on Li metal was taken from an Internet source [51] , without proper credits, from Callcot and Arakawa (C&A) [52] and from Mathewson and Myers [53] . The data was measured, most probably, at room temperature. It is hard to estimate if the density is the nominal density (), for example the work of C&A uses thin films of unspecified density.

In Figure 19 these experimental data are compared with the QMD + FTDFT calculation at and. The goal of the calculations is obviously not to reproduce experimental data at room temperature, nevertheless it is instructive to compare. In spite of the very different conditions, the calculation does not depart wildly from the experiment. The C&A [52] data is

devided by its authors in two regions. In the range, The data is considered by the authors as very reliable. In the range below 6 eV, C&A working with two different substrates for their thin films, obtained two different branches of data, one numerically larger than the other. It seems that [51] includes the reliable part of [52] .

5. Summary

This work presents Quantum Molecular Dynamics and Finite Temperature DFT calculations, from which optical and electrical properties of warm Lithium plasma are obtained. It covers a range of temperatures and densities not in- vestigated previously bringing, therefore, fresh new information on dense plasma

characteristics.

Detailed theoretical backgrounds were discussed:

・ Specifically the connections between the calculations and the dielectric func- tion.

・ Extraction of the optical properties from the dielectric function.

・ Use of pseudopotentials both in the QMD and the DFT calculations.

・ Strength and the problems in using the PAW pseudopotential for the DFT and the dielectric function calculations.

Moreover, also other computational techniques, of more heuristic approach, were employed resulting in a formula for Lithium Equation of State at high temperature and densities.

Whenever possible comparison with experimental data was shown, even when the temperature range was different.

Conclusion: New theoretical data for Rosseland absorption mean, indexes of refraction, , dielectric function and an equation of state are offered for Lithium in an unexplored range of temperatures and pressures.

Acknowledgements

I am grateful to Dr. Yuri Ralchenko from NIST, for his help with the FLYCHK program.

Cite this paper

Kahane, S. (2017) Quantum Molecular Dynamics Simulations of Warm Dense Li Plasma. Open Journal of Modelling and Simulation, 5, 189-217. https://doi.org/10.4236/ojmsi.2017.54015

References