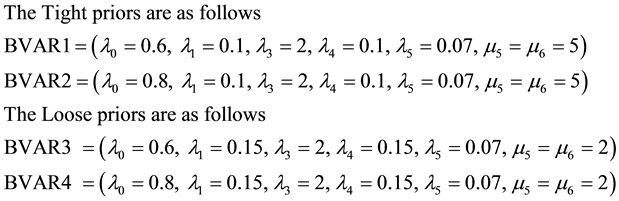Open Journal of Modelling and Simulation
Vol.03 No.04(2015), Article ID:60114,12 pages
10.4236/ojmsi.2015.34016
A Simulation Study on the Performances of Classical Var and Sims-Zha Bayesian Var Models in the Presence of Autocorrelated Errors
M. O. Adenomon*, V. A. Michael, O. P. Evans
Department of Mathematics & Statistics, The Federal Polytechnic, Bida, Nigeria
Email: *admonsagie@gmail.com, vicronz@yahoo.com, patevansjj@gmail.com
Copyright © 2015 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 11 August 2015; accepted 27 September 2015; published 30 September 2015
ABSTRACT
It is well known that a high degree of positive dependency among the errors generally leads to 1) serious underestimation of standard errors for regression coefficients; 2) prediction intervals that are excessively wide. This paper set out to study the performances of classical VAR and Sims-Zha Bayesian VAR models in the presence of autocorrelated errors. Autocorrelation levels of (−0.99, −0.95, −0.9, −0.85, −0.8, 0.8, 0.85, 0.9, 0.95, 0.99) were considered for short term (T = 8, 16); medium term (T = 32, 64) and long term (T = 128, 256). The results from 10,000 simulation revealed that BVAR model with loose prior is suitable for negative autocorrelations and BVAR model with tight prior is suitable for positive autocorrelations in the short term. While for medium term, the BVAR model with loose prior is suitable for the autocorrelation levels considered except in few cases. Lastly, for long term, the classical VAR is suitable for all the autocorrelation levels considered except in some cases where the BVAR models are preferred. This work therefore concludes that the performance of the classical VAR and Sims-Zha Bayesian VAR varies in terms of the autocorrelation levels and the time series lengths.
Keywords:
Simulation, Performances, Vector Autoregression (VAR), Classical VAR, Sims-Zha Prior, Bayesian VAR (BVAR), Autocorrelated Errors

1. Introduction
Autocorrelation plays significant role in both time series and cross sectional data [1] . More often autocorrelation renders the inferences and decision making about the estimated parameters invalid [2] . In addition, it is well known that a high degree of positive dependency among the errors generally leads to 1) serious underestimation of standard errors for regression coefficients; 2) prediction intervals that are excessively wide [3] . While Gujarati, [4] identified the several reasons that make autocorrelation to occur. They are Inertia, Specification Bias, Excluded variables, incorrect functional form, cobweb phenomenon, lags, data transformation/manipulation, and nonstationarity.
In the time series literature, the standard linear regression model, autocorrelation of the disturbances leads to inefficient but still unbiased estimates of the coefficient [5] , while the Least squares estimation of parameters in the general linear model may be highly inefficient in the presence of autocorrelated errors [6] . In the work of Smith, Wong and Kohn, [7] revealed that when a regression model is fitted to time series data the errors are likely to be autocorrelated. In a recent work of Garba et al. [8] , they observed that the autocorrelation problem usually afflict time series data, while in a similar study carried out by Adenomon & Oyejola [9] , they concluded that classical VAR model tend to forecast where there is no autocorrelation while the Bayesian VAR models with harmonic decay forecast better for both negative and positive autocorrelation level.
This paper therefore studied the forecasting performances of the classical VAR and some versions of Sims- Zha Bayesian VAR with quadratic decay models for bivariate time series with AR(1) error terms using Monte- Carlo experiment.
2. Model Description
2.1. Vector Autoregression (VAR) Model
Given a set of k time series variables,
 , VAR models of the form
, VAR models of the form
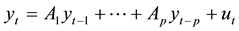 (1)
(1)
provide a fairly general framework for the Data General Process (DGP) of the series. More precisely this model
is called a VAR process of order p or VAR(p) process. Here
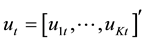 is a zero mean independent
is a zero mean independent
white noise process with non singular time invariant covariance matrix ∑u and the Ai are (k ´ k) coefficient matrices. The process is easy to use for forecasting purpose though it is not easy to determine the exact relations between the variables represented by the VAR model in Equation (1) above [10] . Also, polynomial trends or seasonal dummies can be included in the model.
The process is stable if
 (2)
(2)
In that case it generates stationary time series with time invariant means and variance covariance structure. The basic assumptions and properties of a VAR processes is the stability condition. A VAR(p) processes is said to be stable or fulfils stability condition, if all its eigenvalues have modulus less than 1 [11] .
Therefore, to estimate the VAR model, one can write a VAR(p) with a concise matrix notation as
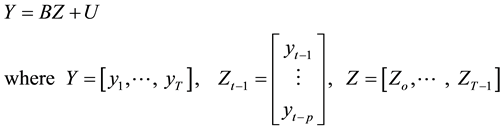 (3)
(3)
Then the Multivariate Least Squares (MLS) for B yields
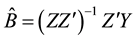 (4)
(4)
2.2. Bayesian Vector Autoregression with Sims-Zha Prior
In recent times, the BVAR model of Sims and Zha [12] has gained popularity both in economic time series and political analysis. The Sims-Zha BVAR allows for a more general specification and can produce a tractable multivariate normal posterior distribution. Again, the Sims-Zha BVAR estimates the parameters for the full system in a multivariate regression [13] .
Given the reduced form model
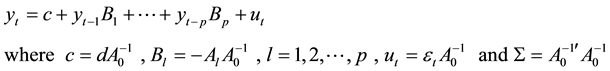
The matrix representation of the reduced form is given as
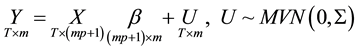
We can then construct a reduced form Bayesian SUR with the Sims-Zha prior as follows. The prior means for the reduced form coefficients are that B1=I and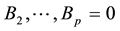 . We assume that the prior has a conditional structure that is multivariate Normal-inverse Wishart distribution for the parameters in the model. To estimate the coefficients for the system of the reduced form model with the following estimators
. We assume that the prior has a conditional structure that is multivariate Normal-inverse Wishart distribution for the parameters in the model. To estimate the coefficients for the system of the reduced form model with the following estimators

where the Normal-inverse Wishart prior for the coefficients is

This representation translates the prior proposed by Sims and Zha form from the structural model to the reduced form ([13] [14] and [12] [15] ).
The summary of the Sims-Zha prior is given in Table 1.
3. Simulation Procedure
A bivariate time series data that have autocorrelated error of order 1 were simulated using the VAR (2) process of the form:

Such that
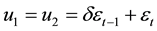 where
where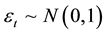 . the choice here is similar to the work and illustration of Cowpertwait, [16] . This work considered ten autocorrelated levels as d = (−0.99, −0.95, −0.9, −0.85, −0.8, 0.8, 0.85, 0.9, 0.95, 0.99) for short term (T = 8, 16); medium term (T = 32, 64) and long term (T = 128, 256). Sample of generated data are presented in Table 2.
. the choice here is similar to the work and illustration of Cowpertwait, [16] . This work considered ten autocorrelated levels as d = (−0.99, −0.95, −0.9, −0.85, −0.8, 0.8, 0.85, 0.9, 0.95, 0.99) for short term (T = 8, 16); medium term (T = 32, 64) and long term (T = 128, 256). Sample of generated data are presented in Table 2.
Table 1. Hyperparameters of sims-zha reference prior.
Source: Brandt and Freeman, [13] .
Table 2. Sample of generated data for T = 8.
Model Specification
The time series were generated data using a VAR model with lag 2. The choice here is to obtain a bivariate time series with the true lag length. While the VAR and BVAR models of lag length of 2 was used for modeling and forecasting purpose.
For the BVAR model with Sims-Zha prior, we consider the following range of values for the hyperparameters given below and the Normal-Inverse Wishart prior was employed.
We consider two tight priors and two loose priors as follows:
where nµ is prior degrees of freedom given as m + 1 where m is the number of variables in the multiple time series data. In work nµ is 3 (that is two (2) time series variables plus 1(one)).
Our choice of Normal-Inverse Wishart prior for the BVAR models follow the work of Kadiyala & Karlsson, [17] that Normal Wishart prior tends to performed better when compared to other priors. In addition Sims and Zha, [12] proposed Normal-Inverse Wishart prior because of its suitability for large systems while Breheny, [18] reported that the most advantage of wishart distribution is that it guaranteed to produce positive definite draws. Our choice of the overall tightness
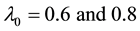
The following are the criteria for Forecast assessments used:
1) Mean Absolute Error (MAE) has a formular
2) The Root Mean Square Error (RMSE) is given as
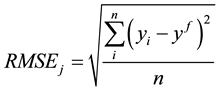
For the two measures above, the smaller the value, the better the fit of the model [24] .
In this simulation study,
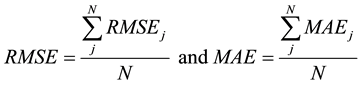
4. Results and Discussion
The entire simulation and analysis was carried out in R environment. The values of the RMSE and MAE for short, medium and long terms are presented in Tables A1-A3 respectively in Appendix A. While the ranks for short, medium and long terms are presented in Tables B1-B3 respectively in Appendix B. In general the values of the RMSE and MAE increased as a result of increase in the autocorrelated levels. In addition the values of the RMSE and MAE decreased as a result of increase in the time series lengths.
The preferred model for short, medium and long terms are presented in Tables 3(a)-(c) respectively.
Table 3(a) revealed that the BVAR model with loose prior (BVAR4) is preferred for negative autocorrelation levels except in few cases, while BVAR model with tight prior (BVAR1) is preferred for positive autocorrelation levels in the short term
In Table 3(b), the BVAR model with loose prior (BVAR4) is preferred for autocorrelation level of −0.99, −0.99 and from 0.9 to 0.99. The classical VAR (VAR(2)) is preferred for autocorrelation levels of −0.8 to 0.85 for T = 64. While in other autocorrelation levels the preferred models varies among BVAR models with tight prior, classical VAR and BVAR model with loose prior respectively.
Table 3. (a) The preferred models for short term (T = 8, 16); (b) The preferred models for medium short (T = 32, 64); (c) The preferred models for long short (T = 128, 256).
In Table 3(c), the classical VAR (VAR(2)) model is preferred for autocorrelation levels of −0.85 to 0.9, the BVAR model with loose prior (BVAR4) is preferred for autocorrelation levels of 0.95 and 0.99. while in other autocorrelation levels the preferred models varies among BVAR models with loose prior, BVAR models with tight prior and the classical VAR model respectively.
5. Conclusions and Recommendation
In conclusion, the performances of the forecasting models depend on the autocorrelation levels and the time series length.
It is therefore recommended that the autocorrelation levels and the time series length should be considered in using an appropriate model for forecasting.
Acknowledgements
We wish to thank TETFUND Abuja-Nigeria for sponsoring this research work. Our appreciation also goes to the Rector and the Directorate of Research, Conference and Publication of the Federal Polytechnic Bida for giving us this opportunity to undergo this research work.
Cite this paper
M. O.Adenomon,V. A.Michael,O. P.Evans, (2015) A Simulation Study on the Performances of Classical Var and Sims-Zha Bayesian Var Models in the Presence of Autocorrelated Errors. Open Journal of Modelling and Simulation,03,146-158. doi: 10.4236/ojmsi.2015.34016
References
- 1. Oloyede, I. and Yahya, W.B. (2015) Bayesian Generalized Least Squares with Autocorrelated Error. Book of Abstract of the 34th Annual Conference of the Nigerian Mathematical Society (NMS), 23-26 June 2015.
- 2. Okorie, C.E., Abubakar, U.Y and Adetutu, O.M. (2015) Analysis of Autocorrelated Data. Book of Abstract of the 34th Annual Conference of the Nigerian Mathematical Society (NMS), 23-26 June 2015.
- 3. Huitema, B.E., Mckean, J.W. and Zhao, J. (1996) The Runs Test for Autocorrelated Errors: Unacceptable Properties. Journal of Educational & Bahaviourial Statistics, 21, 390-404.
http://dx.doi.org/10.3102/10769986021004390 - 4. Gujarati, D.N. (2003) Basic Econometrics. 4th Edition, The McGraw-Hill Co., New Delhi.
- 5. Rao, P. and Griliches, Z. (1969) Small-Sample Properties of Several Two-Stage Regression Methods in the Context of Autocorrelated Errors. Journal of American Statistical Association, 64, 253-272.
http://dx.doi.org/10.1080/01621459.1969.10500968 - 6. Berenblut, I.I. and Webb, G.I. (1973) A New Test for Autocorrelated Errors in the Linear Regression Model. Journal of Royal Statistical Society B, 35, 33-50.
- 7. Smith, M., Wong, C.-M. and Kohn, R. (1998) Additive Non-Parametric Regression with Autocorrelated Errors. Journal of Royal Statistical Society B, 60, 311-331.
http://dx.doi.org/10.1111/1467-9868.00127 - 8. Garba, M.K., Oyejola, B.A. and Yahya, W.B. (2013) Investigations of Certain Estimators for Modelling Panel Data Under Violations of some Basic Assumptions. Mathematical Theory and Modeling, 3, 47-53.
- 9. Adenomon, M.O. and Oyejola, B.A. (2015) Forecasting Bivariate Time Series with AR(1) Error Terms. A Paper Presented at the 39th Annual Conference of the Nigerian Statistical Association (NSA), Osun State, 9-11 September 2015.
- 10. Lutkepohl, H. and Breitung, J. (1997) Impulse Response Analysis of Vector Autoregressive Processes: System Dynamic in Economic and Financial Models.
- 11. Yang, M. (2002) Lag Length and Mean Break in Stationary VAR Models. The Econometrics Journal, 5, 374-386.
http://dx.doi.org/10.1111/1368-423X.00089 - 12. Sims, C.A. and Zha, T. (1998) Bayesian Methods for Dynamic Multivariate Models. International Economic Review, 39, 949-968.
http://dx.doi.org/10.2307/2527347 - 13. Brandt, P.T. and Freeman, J.R. (2006) Advances in Bayesian Time Series Modeling and the Study of Politics: Theory, Testing, Forecasting and Policy Analysis. Political Analysis, 14, 1-36.
http://dx.doi.org/10.1093/pan/mpi035 - 14. Brandt, P.T. and Freeman, J.R. (2009) Modeling Macro-Political Dynamics. Political Analysis, 17, 113-142.
http://dx.doi.org/10.1093/pan/mpp001 - 15. Sims, C.A. and Zha, T. (1999) Error Bands for Impulse Responses. Econometrica, 67, 1113-1155.
http://dx.doi.org/10.1111/1468-0262.00071 - 16. Cowpertwait, P.S.P. (2006) Introductory Time Series with R. Springer Science + Business Media, LLC., New York.
- 17. Kadiyala, K.R. and Karlsson, S. (1997) Numerical Methods for Estimation and Inference in Bayesian VAR Models. Journal of Applied Econometrics, 12, 99-132.
http://dx.doi.org/10.1002/(SICI)1099-1255(199703)12:2<99::AID-JAE429>3.0.CO;2-A - 18. Breheny, P. (2013) Wishart Priors. BST 701: Bayesian Modelling in Biostatistics.
http://web.as.uky.edu/statistics/users/pbreheny/701/S13/notes/3-28.pdf - 19. Brandt, P.T., Colaresi, M. and Freeman, J.R. (2008) Dynamic of Reciprocity, Accountability and Credibility. Journal of Conflict Resolution, 52, 343-374.
http://dx.doi.org/10.1177/0022002708314221 - 20. Merkin, J.H. and Needman, D.J. (1990) The Development of Travelling Waves in a Simple Isothermal Chemical System II. Cubic Autocatalysis with Quadratic and Linear Decay. Proceedings: Mathematical & Physical Sciences, 430, 315-345.
- 21. Merkin, J.H. and Needman, D.J. (1991) The Development of Travelling Waves in a Simple Isothermal Chemical System IV. Quadratic Autocatalysis with Quadratic Decay. Proceedings: Mathematical & Physical Sciences, 434, 531-554.
- 22. Worsley, K.J., Evans, A.C., Strother, S.C. and Tyler, J.L. (1991) A Linear Spatial Correlation Model with Applications to Positron Emission Tomography. Journal of the American Statistical Association, 86, 55-67.
http://dx.doi.org/10.1080/01621459.1991.10475004 - 23. Caraiani, P. (2010) Forecasting Romanian GDP Using a BVAR Model. Romanian Journal of Economic Forecasting, 4, 76-87.
- 24. Cooray, T.M.J.A. (2008) Applied Time Series Analysis and Forecasting. Narosa Publishing House, New Delhi.
Appendix A
Table A1. RMSE and MAE of the Models for short term (T = 8, 16)
Table A2. RMSE and MAE of the models for medium term (T = 32, 64).
Table A3. RMSE and MAE of the models for Long term (T = 128, 256).
Appendix B
Table B1. Ranks of RMSE and MAE of the Models for short term (T = 8, 16).
Table B2. Rank of RMSE and MAE of the models for medium term (T = 32, 64).
Table B3. Ranks of RMSE and MAE of the Models for Long term (T = 128, 256)
NOTES
*Corresponding author.