Open Journal of Modelling and Simulation
Vol.03 No.01(2015), Article ID:52414,6 pages
10.4236/ojmsi.2015.31002
A Lecture of the Taylor Rule from the Sandpile Model
Juan L. Valderrábano López, Miguel Ángel Alonso Neira
Departamento de Economía Aplicada I, FF CC Jurídicas y Sociales, URJC, Paseo Artilleros s/n. Vicálvaro (Madrid), Spain
Email: jl.valderrabno@alumnos.urjc.es
Academic Editor: Antonio Hervás Jorge, Department of Applied Mathematics, Universidad Politécnica de Valencia, Spain
Copyright © 2015 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 13 October 2014; revised 8 November 2014; accepted 12 December 2014
ABSTRACT
Sandpile phenomena in dynamic systems in the vicinity of criticality always appeal to a sudden break of stability with avalanches of different sizes due to minor perturbations. We can view the intervention of the Central Banks on the rate of interest as a perturbation of the economic system. It is an induced perturbation to a system that fare in vicinity of criticality according to the condi- tions of stability embedded in the equations of the neoclassical model. An alternative reading of the Taylor Rule is proposed in combination with the Sandpile paradigm to give an account of the economic crisis as an event like an avalanche, that can be triggered by a perturbation, as is the intervention of the Central Bank on the interest rate.
Keywords:
Critical Phenomena, Sandpile Model, Taylor Rule, Central Banks, Power Law

1. Modeling the Economy
In Science we are familiar with axiomatic theories where knowledge is encapsulated in form of theorems obtained from a small set of axioms. We check the validity of them against the results obtained by means of experiments. In other branches of sciences we can apply the logical deductive method but, there is not such a thing as an experiment, to validate theoretical outcomes. We have recorded observations, and try to identify theories that comply with the past facts. The nature of the observations can be qualitative or quantitative, but both offer information good enough to pursue the discovering process in the search of good theories. It is like Mendel’s laws without knowing the genome structure. After that discovery, the Principle of Hardy Weinberg completes the job.
As E. O. Wilson points out “scientists look for four qualities in theory generally and mathematical models in particular” and one of them is Consilience by which “units and processes of a discipline that conforms with solidly verified knowledge in other disciplines have proven consistently superior in theory and practice to units than do not conform”.
Catastrophes as the tsunamis and other geological shocks are a common experience, and so the economic crisis, the burst, as explained by N. Roubini: “…the irrational euphoria, the pyramids of leverage, the financial innovations, the asset price bubbles, the panics and the runs on banks and other financial institutions…are common to many other disasters as well. Change a few particulars of the foregoing narrative, and you could be reading about the infamous South Sea Bubble of 1720, the global financial crisis of 1825, the boom and bust that foreshadowed Japan’s Lost Decade (1991-2000), the American savings and loan crisis, or the dozen of crisis that hammered emerging markets in the 1980s and 1990s”. In consequence there is nothing strange or wrong in the idea of searching for models that can describe the formation of “bubble-like” phenomena and its dissipation (burst), and move them to the realm of Economy.
We do have the conceptual model of the Sandpile. It is a very well established model to deal with dynamical systems near criticality that dissipate violently when a break of stability occurs. The dynamic is local, but the process is global. It describes what occurs without connection to the inner forces of the system but we only observe aggregated facts i.e. avalanches. In addition, a salient characteristic of the sandpile model is that the observations or results are ruled out by the Potential Law, allowing tail events to happen.
In the case of the Economy, we have find out an example of an event where a process as the sandpile fits in, not only from the point of view of the narrative but also from the few available facts. We know that the money piles up in “pyramids of leverage” but behind this fact should exist an economic process creating money. Searching for a mechanism to built up such pyramids of money, we have seen a way for that. The Taylor Rule (TR) is used by the Central Banks to set up inflation or interest rates targets, that indirectly affects to the amount of money in the market. The Taylor Rule remembers the way in which the sand piles up. So we have set up a connection between goal setting for the Tayor Rule and a critical condition related to the mass of money, that when overcomed can drive the system out of equilibrium. This behaviour is far from the equilibrium and it is allowed by the Potential Law, because the Gaussian distribution almost forbid events in the tails.
In what follows there is a brief account of the Sandpile model based on the ideas presented in two seminal papers [1] [2] , about self-organized criticality in order to use them as a bedrock for an interpretation of the Taylor Rule in economics. Later we connect it to the effect of the Taylor Rule and the Potential Law.
1.1. The Model
There are two things we want to emphasize about the model.
First is the simplicity, and the narrative. “Consider a pile of sand in a table where sand is added slowly, starting from a flat configuration. Initially the grains of sand will stay more or less where they land; when the pile becomes steeper, small avalanches or sandslides, occur. The addition of a single grain of sand can cause a local disturbance but nothing dramatic happens. Eventually the system reaches a statistically stationary state, where the amounts of sand added is balanced, on average, by the amount of sand leaving the system along the edges of the table. In this stationarty state, there are avalanches of all sizes, up to the size of the entire system. The collection of grains has been transformed from one on where the individual grains follow their own independent dynamics, to one where the dynamics is global.”
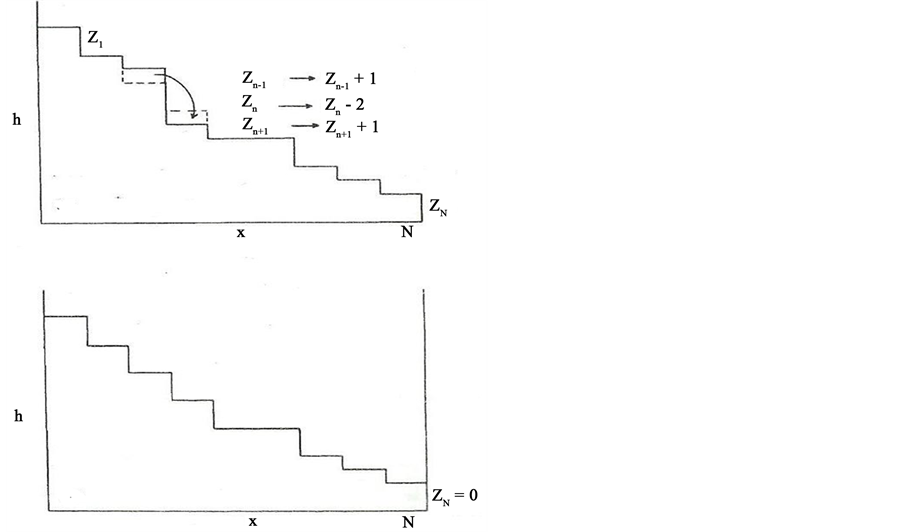
Figure 1 shows a model of a one-dimensional sandpile of length N. The boundary conditions are such that sand can leave the system at the right-hand side only. We may think as this arrangement as half of a symmetric sandpile with both ends open. The numbers z(n) represent height differences:
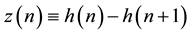
between two successive positions along the sandpile. The dynamics is very simple. From the figure one sees that sand is added at the nth position by letting
 (1)
(1)
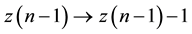 (2)
(2)
When the height difference becomes higher than a fixed critical value zcr one sand unit tumbles to the lower level, i.e.,
Figure 1. The sandpile dynamics and boundary conditions.
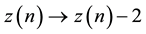 (3)
(3)
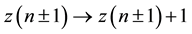 (4)
(4)
for .
.
It is worth to note that as it is explained that: “the particular (toppling) rule we use is not important”.
Closed and open boundary conditions are used for the left and right boundaries, respectively,
 (5)
(5)
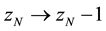 (6)
(6)
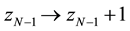 (7)
(7)
for
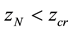 (8)
(8)
The process continue until all the z(n) are below the threshold, at which point another grain of sand is added (at a random site) via Equations (1) and (2).
Second is a result associated with the dynamic of the model. “At each time step the height at some random point is increased in one unit z → z + 1. If the height at that site now exceeds an arbitrary critical heigth zcr then a toppling event occurs where the height of the unstable site is reduced and the height of its neighbors is increased” (in the one dimensional model both in one unit). “If any of the neighboring sites are now unstable (z > zcr) the process continues until none of the z values in the system exceeds the critical value. Then the avalanche is over, and a new avalanche can be started by adding another grain of sand to the system. The total number of topplings during the avalanche is counted; this number, s, is the size of the avalanche”. “We made an histogram and found that the distribution of the events where a total of s sites topple obeys a power law P(s) » s−t. Thus if one waits long enough, one is bound to see events that are as large as one has the patience to wait for.”
1.2. How We Do Read the Sandpile Model
In order to establish a parallelism between self-organized critical phenomena and some of the events we do find in Economics, we need to read the sandpile model in another way. In Economics, as in many other fields we are familiar with the fact that many subsystems we do observe, behave in a similar way to the sandpile but we do not observe the details; instead we are familiar with aggregated behaviour and data. As the Economy grows there are processes and transactions inside the system piling up without presenting any symptom of unstability reaching out progressively greater levels of complexity. Price formation is an example. We do measure and observe aggregated or extended variables, such as the Gross Domestic Product (GDP), inflation and interest rates, that we cannot connect with the inner working of the system. Minor perturbations or changes trigger crisis time and again, that remind us or we can associate to, avalanches. So let’s see what we can draw from the sandpile model.
In the sandpile model, we have a system defined at least by one observable parameter h(n) associated to a generalized coordinate n. Also we have a function z(n) defined as:

where in the case of complete or limit configuration every z(n) = 1. If we add the values of z(n) we have

Should the value of the function z(n) for a point be greater than a critical value zcr the system enter into a dissipative mechanism, described for a sandpile as the transformation rules (3) and (4) also called toppling rule. It has been pointed out by the authors that the particular toppling rule we use is not very important. Let think we
are building the sandpile, so piling up sandgrains. We can consider we have two instances with  and
and  while adding grains on the top of the pile. The difference between the two configurations
while adding grains on the top of the pile. The difference between the two configurations  does not matter as long as the local critical condition is not violated. In any case
does not matter as long as the local critical condition is not violated. In any case
when we go beyond the limit for a point and zaggregated > N an avalanche is triggered. We can then consider N as an aggregated limit for this case. The nature and value of zcr is tied to the local phenomenon under study, being the slope of the pile in the case of a sandpile, but in general can be thought as value of a variable, related to something we can measure or observe in the aggregated system under consideration. The sandpile model links what happens i.e. the dropping of a grain of sand or local perturbation, and what we do observe i.e. an avalanche, described by transformation (3) and (4). There is not any connection between the internal workings of the sandpile and the transformation shown by (3) and (4).
2. Taylor Rule
We do refer to a complete description of the matter in the available literature [3] . As explained in the original paper the rule describes very well the behaviour of the US Federal Reserve in the period 1987-1992. The rule states that interest rates tend to increase with inflation and to decrease with slack economic activity. We do accept that the Taylor Rule can interpret reasonably well the economic reason, and under certain circumstances can offer good advice. The rule sates that:
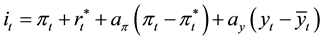
where it is the target short-term nominal interest rate (federal funds rate in the US), 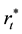
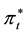
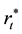


As far as we know there are not considerations or constraints about the relationship between the amounts or variables included in the Taylor Rule and the state of the Economy such as the aggregated Demand or aggregated Investment level and others.
We can reinterpret the rule in the following way.
We can look at the expression (9) first as 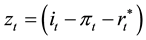
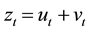
where the term:
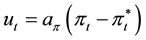
seems to us very familiar with the standard function used for the sandpile in the case of inflation but referring to an isolated or extended value, and the term:

has a similar form to the sandpile. The term points out also, to a familiar aggregated value. It is easy to see that expression (9) can be seen as a generalized sandpile rule to higher dimensions. Then setting up the target or forecast for aggregated values is tantamount as guessing where the critical value lies in, and in consequence we can be in this sense, over or below this value. Accordingly we can reason that if an avalanche has occurred in the past we went over this unknown critical value. It is our opinion that both terms (10) and (11) can serve as indicators to trigger and avalanche or economic crisis, although we are not concerned with the nature of the toppling rule at this moment, because as mentioned previously it is not very important. Then we are going to establish a link between two events, going beyond the target and triggering an avalanche. Let’s see how that should come.
3. The IS-LM Model
In order to illustrate the relationship between the sandpile model and the Tayor Rule, as explained in the original paper the rule describes very well the behaviour of the US Federal Reserve in the period 1987-1992. The rule states that: interest rates tend to increase with inflation and to decrease with slack economic activity. We do accept that the Taylor Rule can interpret reasonably well the economic reason, and under certain circumstances can offer good advice. The Taylor restriction it is necessary to search for help in order to built up a critical value zcr beyond which the pile collapses.
Lets take the equations for the of the most popular Neoclassical dynamic Model the Investment Savings and Liquidity Monetary Mass (IS-LM) as expressed in [4] :
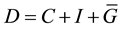

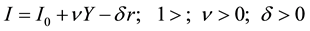
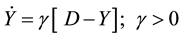
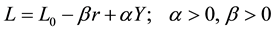
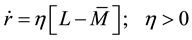
Being the variables of the model: Demand, Consumption, Government Expenses, Investment, Liquidity, the rent Y and the interest rate r and the rest symbols are the unknown numerical parameters c, ν, δ, γ, β, η.
We can rewrite the equations in the following way:
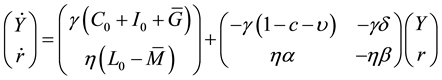
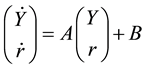
This set of differential equations describes the dynamics of the system. One condition for stability is Tr(A) < 0 being:

It is the addition of two terms of parameters, the first term coming from the goods market, and the second from the money market, the combination of both providing a cue for stability or unstability i.e. both markets must balance each other to drive Tr(A) < 0. One case for unstability is the following: Should the first term be positive under the condition (c + ν) > 1 that means that “each dollar increase in supply causes an increase in demand in excess of its own magnitude” [5] , unless the absolute value of the second term would be greater than the first, then Tr(A) > 0 or the system is unstable. Regarding the second term ηβ the parameter η according to (17)
links the speed of adjustment of the interest r in function of the distance 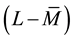
the monetary mass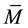
the interest rate appeal to an increase of liquidity L that in turn makes greater the distance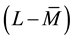
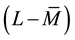
tered by the increment of L, and that in turn reduces the weight of η. An Economy strongly leveraged demands a higher speed move from the interest rate, or the money market cannot counterbalance the effect of an oversized demand in the goods market, driving the system into a crisis.
The toppling rule can thus be read as: A crisis can occur when the Central Bank intervenes setting targets or goals against the nature of the system. When the leverage is high and there is a Demand in excess because borrowing beyond the limits, the system is prone to instability. Leveraging and of course the amount of liquidity is asking for a rapid increase of interest rates in order to compensate the Demand in excess, and if the intervention of the Central Bank is backwards, is the seed for instability. This how lighting a fire.
4. Conclusion―How the Pieces Fit Together
Now its time to put all the pieces together.
First of all we must warn that the values of the parameters in (20) are not known accurately and that consequently we can only establish a guess based on indirect appraisal.
We have a model as the sandpile that according to our experience describes very well the dynamics of the self-organized critical systems. We do understand that the Economy is one of such, and that in order to draw theoretical conclusions it would be good to define the ingredients of the sandpile model viewed from the Economy. Then it should be first necessary at least, to identify a function or rule that helps to build the sandpile, second a critical value to overcome, and finally, if possible, a toppling rule.
Then the Taylor Rule seems to be a good candidate in order to comply with the first condition. As pointed out, the stability condition (20) stemming from the IS-LM model can serve as the second. The values forecasted by the Taylor Rule can drive the system, the aggregated behaviour as described by the IS-LM equations, into un-
stability, if we break the stability condition (20). In our opinion 
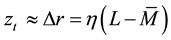
tering it. This value can be greater or lower than the value of Dr requested by the self adjusting economic system. The value of Dr for an economy strongly leveraged should be big enough to produce a ratio η such that can compensate the drift of a demand greater than the rent, otherwise the system is prone to instability. A changing h can be considered a case of bifurcation. It is worth to remark the contingency of the approach.
As per the available data the US Economy went through the following crisis [6] (expansions and contractions):
1854-2009 (33 cycles)
1854-1919 (16 cycles)
1919-1945 (6 cycles)
1945-2009 (11 cycles)
And accordingly to the original paper the Taylor Rule was explaining well the behaviour of the Federal Reserve in the period between 1987 and 1992 where one crisis occurred. Then we know that tail events are allowed, so this is something to count on, in favour of a model that exhibits a Power Law distribution.
It is worth to analyze the crisis between July 1990 and March 1991 in the light of the comment, because the two conditions for the unstability hold. First the US economy was following the debt path growth of the last 25 years, so demand was higher than rent, and there was a continuous decline between 1989 and 1992 of the Federal Funds Rate (FFR) [7] . As expected according to the sandpile model a crisis could be triggered. This paper illustrates a potential mechanism that could explain the ensued crisis between 1990 and 1991.
Anyway as already expressed the lack of a toppling rule it is not an indispensable to validate the model. We know it happens, we don’t exactly know how. On top of that it is a pity we cannot count on with formal statistics about the severity of the crisis, just with the observation that they do occur, then questioning the use of Gaussian stat in favour of the potential law as per in the sandpile model.
So we have avalanches, a forming rule and a critical condition to overcome, pointing to that the underlying phenomena, can be described as belonging to the family of complex phenomena such as the described by the principle of emergence and bifurcation.
A. Greenspan wrote [8] that: I believe that the Taylor Rule is a useful first approximation to the path of monetary policy, its parameters and predictions derive from model structures that have been consistently unable to anticipate the onset of recessions and financial crisis. This is in agreement with what we have commented previously.
Acknowledgements
We want to thank to Emeritus Prof. Dr. José Manuel Guerra Pérez for his helpful discussions on the matter. Also we are greatly indebted to Dr. Eduardo Cabrera Granado for his hepful assistance in the preparation of the manuscript.
References
- Bak, P. and Paczuski, M. (1995) Complexity, Contingency, and Criticality. Proceedings of the National Academy of Sciences, 92, 6689-6696. http://dx.doi.org/10.1073/pnas.92.15.6689
- Bak, P., Tang, C. and Wiesenfeld, K. (1988) Self-Organized Criticality. Physical Review A, 38, 364-374. http://dx.doi.org/10.1103/PhysRevA.38.364
- Alonso González, L.A. and García Martínez, P. (2004) Central Bank Independence: Taylor Rule and Fiscal Policy, Documentos de trabajo de la Facultad de Ciencias Económicas y Empresariales 04-01, Universidad Complutense de Madrid, Facultad de Ciencias Económicas y Empresariales. http://eprints.ucm.es/6817/1/0401.pdf
- Ferguson B.S. and Lim, G.C. (1998) Introduction to Dynamic Models. Manchester University Press, Manchester, M13 9NR, UK.
- Ferguson B.S. and Lim, G.C. (1998) Introduction to Dynamic Models. Manchester University Press, Manchester, M13 9NR, UK, 130.
- http://www.nber.org/cycles/cyclesmain.html
- http://research.stlouisfed.org/fred2/series/FEDFUNDS
- Greespan, A. http://online.wsj.com/articles/SB123672965066989281