Open Journal of Modelling and Simulation
Vol.1 No.3(2013), Article ID:34305,3 pages DOI:10.4236/ojmsi.2013.13005
Interrelation of Languages of Colored Petri Nets and Some Traditional Languages
1Faculty of Mathematics, Physics and Informatics, Armenian State Pedagogical University after Kh. Abovyan, Yerevan, Armenia
2Seismology, Institute of Geophysics and Engineering Seismology after A. Nazarov of NAS RA, Gyumri, Armenia
Email: petrosyan_gohar@list.ru, lilit@sci.am
Copyright © 2013 Goharik R. Petrosyan et al. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Received January 29, 2013; revised February 28, 2013; accepted March 7, 2013
Keywords: Petri Nets; Colored Petri Nets; Context-Free Languages; Context-Sensitive Languages; Regular Languages
ABSTRACT
The article studies the interrelation of Languages of Colored Petri Nets and Traditional formal languages. The author constructed the graph of Colored Petri Net, which generates L* Context-free language. This language may not be modeled using standard Petri Nets [1]. The Venn graph and diagram that the author modified [1], show the interrelation between languages of Colored Petri Nets and some Traditional languages. Thus the class of languages of Colored Petri Nets is supposed to include an entire class of Context-free languages.
1. Introduction
Petri Nets (PN) is a graphical tool for the formal description of the flow of activities in complex systems. With respect to other more popular techniques of graphical system representation (like block diagrams or logical trees), PN is particularly suited to represent logical interactions among parts or activities in a system in a natural way.
PN used for modeling real systems is sometimes referred to as Condition/Events nets. Places identify the conditions of the parts of the system (working, idling, queuing, and failing), and transitions describe the passage from one condition to another (end of a task, failure, repair...). An event occurs (a transition fires) when all the conditions are satisfied (input places are marked) and give concession to the event. Occurrence of the event completely or partially modifies the status of the conditions (marking). The number of tokens in a place can be used to identify the number of resources lying in the condition denoted by that place. The following examples illustrate typical situations of interaction of activities arising in system modeling [1,2].
The formal definition of a standard Petri nets:
Petri Net 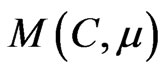 pair, where
pair, where 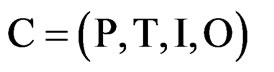 is the network structure and
is the network structure and  is the network condition.
is the network condition.
In structure C of a P-positions, T-transitions are finite sets. 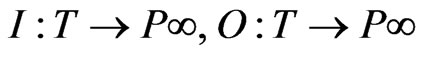 are the input and output functions, respectively, where
are the input and output functions, respectively, where 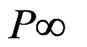 are all possible collections (repetitive elements) of P.
are all possible collections (repetitive elements) of P. 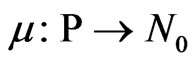 is the function of condition, where
is the function of condition, where 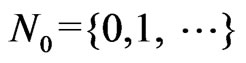 is the set of integers. We determine (in a known manner) the allowed transitions of Petri Nets and the transitions from one state to another, as well as the set of reachable states [1,2].
is the set of integers. We determine (in a known manner) the allowed transitions of Petri Nets and the transitions from one state to another, as well as the set of reachable states [1,2].
Coloured Petri Nets (CPN) is a graphical oriented language for design, specification, simulation and verification of systems [3-8]. It is in particular well-suited for systems that consist of a number of processes which communicate and synchronize. Typical examples of application areas are communication protocols, distributed systems, automated production systems, work flow analysis and VLSI chips.
The CPN language allows the model to be represented as a set of modules, allowing complex nets (and systems) to be represented in a hierarchical manner.
In the classical or traditional Petri Net tokens do not differ from each other, we can say that they are colorless. Unlike standard Petri nets in colored, Petri Net of a position can contain tokens of arbitrary complexity, for example, lists, etc., that enables modeling be more reliable.
2. Definition
The mathematical definition of Colored Petri Net: CPN is a nine-tuple
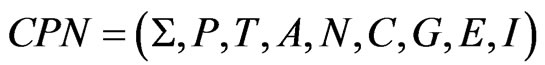
where:
1) ![]() is a finite set of non-empty types, also called color sets. In the associated CPN Tool, these are described using the language CPN-ML [9]. A token is a value belonging to a type.
is a finite set of non-empty types, also called color sets. In the associated CPN Tool, these are described using the language CPN-ML [9]. A token is a value belonging to a type.
2) P is a finite set of places. In the associated CPN Tool these are depicted as ovals/circles.
3) T is a finite set of transitions. In the associated CPN Tool these are depicted as rectangles.
4) A is a finite set of arcs. In the associated CPN Tool these are depicted as directed edges. The sets of places, transitions, and arcs are pairwise disjoint, that is
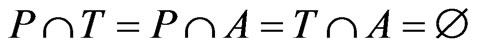 .
.
5) N is a node function. It is defined from A into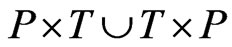 . In the associated CPN Tool this depicts the source and sink of the directed edge.
. In the associated CPN Tool this depicts the source and sink of the directed edge.
6) C is a color function,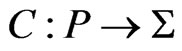 .
.
7) G is a guard function. It is defined from T into expressions such that:
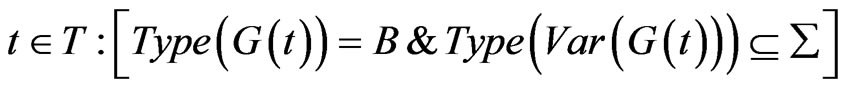
8) E is an arc expression function. It is defined from A into expressions such that:
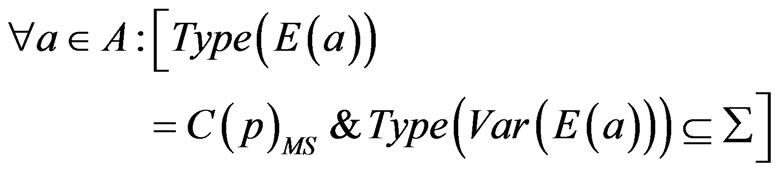
where p is the place of 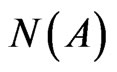 and
and 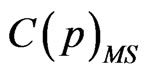 denotes the multi-set type over the base type
denotes the multi-set type over the base type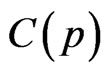 .
.
9) I is an initialization function. It is defined from P into closed expressions so that:
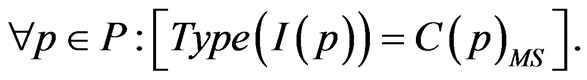
In the CPN Tool this is represented as initial marking next to the associated place.
The distribution of tokens, called marking, in the places of a CPN determines the state of a system being modeled. The dynamic behavior of a CPN is described in terms of the firing of transitions. The firing of a transition takes the system from one state to another. A transition is enabled if the associated arc expressions of all incoming arcs can be evaluated to a multi-set, compatible with the current tokens in their respective input places, and its guard is satisfied. An enabled transition may fire by removing tokens from input places specified by the arc expression of all the incoming arcs and depositing tokens in output places specified by the arc expressions of outgoing arcs.
One of the most studied simple class of formal languages is the class of Regular languages. It is known that any Regular language is the language of Petri Nets [1,10]. It’s possible to construct Petri Net, which generates
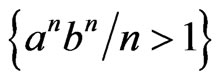 a Context-free language, which is not Regular [1]. Not all the languages of Petri Nets are Context-free, built a network that generates
a Context-free language, which is not Regular [1]. Not all the languages of Petri Nets are Context-free, built a network that generates 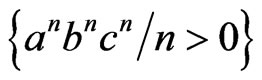 a Context-sensitive language, which is not Context-free language [1]. Unlike Regular languages, which are the languages of Petri Nets, there are Context-free languages, which are not languages of Petri Nets. Such examples of Context-freе language we are noted the following:
a Context-sensitive language, which is not Context-free language [1]. Unlike Regular languages, which are the languages of Petri Nets, there are Context-free languages, which are not languages of Petri Nets. Such examples of Context-freе language we are noted the following:
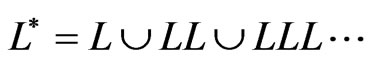
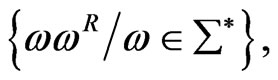 (in particular,
(in particular,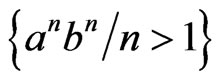 ). This fact illustrates the limitation of Petri Net as a tool, that generates the languages [1].
). This fact illustrates the limitation of Petri Net as a tool, that generates the languages [1].
In Petri Nets is not possible to remember arbitrarily long sequence of arbitrary characters. In Petri Nets the sequence of limited length can be remembered (this is also possible in finite automata) [1].
However, Petri Nets do not have the “capacity of pushdown memory” which is necessary for the generation of Context-free languages. The interrelation of languages of Petri Nets with other classes of languages investigated Ven [1], this is shown in Figure 1 in the form of a diagram.
3. Results
We modeled 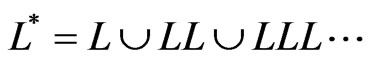 language (star Klin) by CPN, in particular
language (star Klin) by CPN, in particular .
.
The Figure 2 shows a Colored Petri Net, which generates the 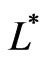 language that is, Colored Petri Net is a more powerful tool than the classical Petri Net. To understand types of data which are used in a figure, it is necessary to give a declaration.
language that is, Colored Petri Net is a more powerful tool than the classical Petri Net. To understand types of data which are used in a figure, it is necessary to give a declaration.
In the figure introduced two positions of count of type and marked as first and second. In the figure, two transitions marked with the symbol a that are generating symbol a, and a transition marked with the symbol b, which generates the symbol b.
In the figure position of count of type remembers the number of transitions are fired and regulates, so the number of appearances a symbol b was equal to the number of appearances a symbol a.
In fact, when the marked with a transition is fired, generates the symbol a, if the marked with b transition is fired, generates the symbol b. To the transitions are attached logical expressions (guards):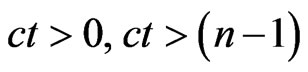 , if the logical expression is true, then the transition is allowed, and if false, then the transition is not allowed. If the first position of count of type value of token is equal to one, the marked with a first transition is fired. The value of n must be fixed advance.
, if the logical expression is true, then the transition is allowed, and if false, then the transition is not allowed. If the first position of count of type value of token is equal to one, the marked with a first transition is fired. The value of n must be fixed advance.
Let n = 2, then is fired marked with a the first transition, and ct = 2, then is fired marked with a the second transition, are generated by aa symbols, in this case second position of count of type value of token is equal to
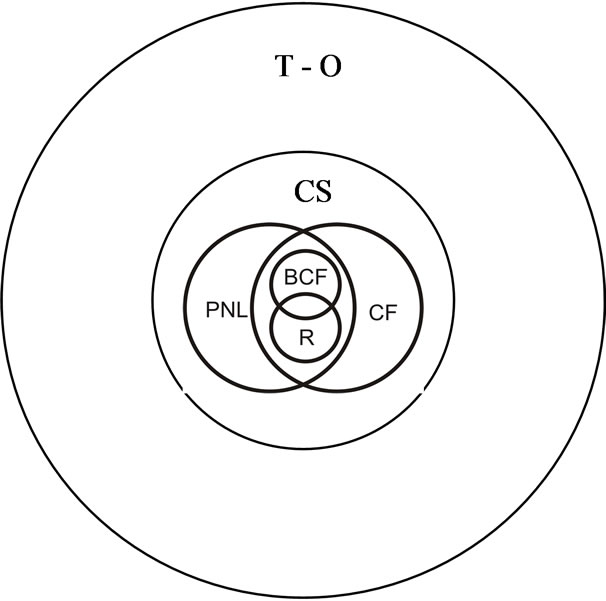
Figure1. Interrelation of Petri nets and traditional languages (T-0—the General type of languages, CS—Contextsensitive languages, PNL—Petri nets languages, CF—Context-free languages, BCF—bonded Context-free languages, R—Regular languages).
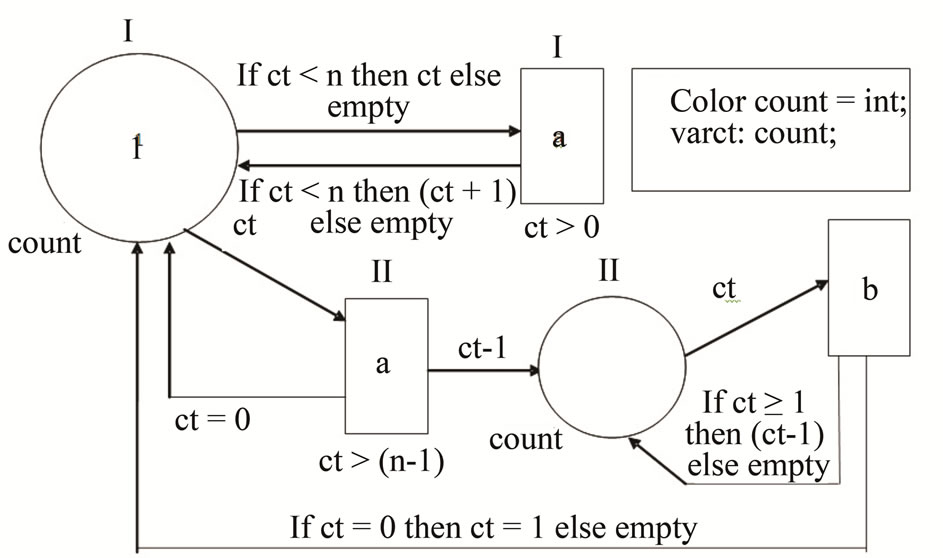
Figure 2. Modeling 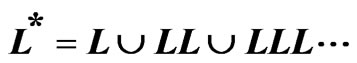 language by Colored Petri Net.
language by Colored Petri Net.
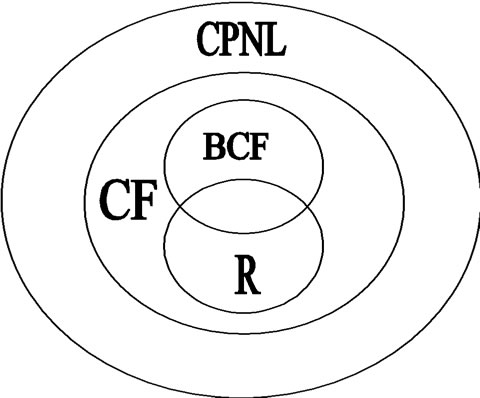
Figure 3. Interrelation of Colored Petri Nets and traditional languages. CPNL (language of Colored Petri Net).
two: count= 2, and twice is fired marked with b the transition, are generated by bb, when the value of the first counter is equal to one, cycle will be repeated, etc.
Many properties of colored Petri nets, as logical expressions, types of markers, the expression of the arcs, etc., which are used to control the transition firing [3].
In Figure 2 Colored Petri Net is constructed for the given language, which supposes following interrelation of languages of Colored Petri Net with some of traditional languages classes (Figure 3).
REFERENCES
- J. L. Peterson, “Petri Net Theory and the Modeling of Systems,” Prentice Hall, Upper Saddle River, 1981.
- T. Murata, “Petri Nets: Properties, Analysis and Applications,” Proceedings of the IEEE, Vol. 77, No. 4, 1989, pp. 541-580. doi:10.1109/5.24143
- K. Jensen, “Coloured Petri Nets: Basic Concepts, Analysis Methods and Practical Use,” Springer-Verlag, Berlin, 1992. doi:10.1007/978-3-662-06289-0
- K. Jensen, “Coloured Petri Nets: Basic Concepts, Analysis Methods and Practical Use. Volumn 1. Basic Concepts. Monographs in Theoretical Computer Science,” SpringerVerlag, Berlin, 1997.
- K. Jensen, “Coloured Petri Nets: Basic Concepts, Analysis Methods and Practical Use. Volumn 2. Analysis Methods Monographs in Theoretical Computer Science,” Springer-Verlag, Berlin, 1997.
- K. Jensen, “Coloured Petri Nets: Basic Concepts, Analysis Methods and Practical Use. Volumn 3. Practical Use. Monographs in Theoretical Computer Science,” SpringerVerlag, Berlin, 1997.
- K. Jensen, “Coloured Petri Nets: A High-level Language for System Design and Analysis,” In: G. Rozenberg, Ed., Advances in Petri Nets 1990, Lecture Notes in Computer Science, Vol. 483, Springer-Verlag, Berlin, 1991, pp. 342-416.
- K. Jensen, “Coloured Petri Nets: A High-level Language for System Design and Analysis,” In: K. Jensen and G. Rozenberg, Eds., High-Level Petri Nets. Theory and Application, Springer-Verlag, Berlin, 1991, pp. 44-122.
- J. D. Ullman, “Elements of ML Programming,” PrenticeHall, Upper Saddle River, 1998.
- A. V. Aho and J. D. Ullman, “Theory of Parsing, Translation, & Compiling,” Prentice Hall, Upper Saddle River, 1973.

