Advances in Historical Studies
Vol.04 No.03(2015), Article ID:57642,27 pages
10.4236/ahs.2015.43015
First Theoretical Constructions to the Fluid Mechanics Problem of the Discharge
Sylvio R. Bistafa
Polytechnic School, University of São Paulo, São Paulo, Brazil
Email: sbistafa@usp.br
Copyright © 2015 by author and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 20 May 2015; accepted 27 June 2015; published 30 June 2015
ABSTRACT
After the publication of Hydrodynamics by Daniel Bernoulli in 1738, there was a fierce competition for priority with his father, Johann Bernoulli, and controversies with Jean le Rond D’Alembert, in which Leonard Euler seemed to have tacitly accepted the role of presiding over the disputes. These disputes were aroused by the almost simultaneous publications of Hydraulics by J. Bernoulli in 1743 and of Traité de l’équilibre et du mouvement des fluides by D’Alembert in 1744. It would be shown that despite the fact that the Bernoullis and D’Alembert used their own principles and approaches to the fluid mechanics problem of discharge, they essentially reached the same end. Nonetheless, it was Euler who brought the fluid mechanics problem of discharge to a new and definitive level with two publications. In these publications, for the first time, the pressure force and the friction force appeared explicitly in the formulations. However, the friction force was built under the wrong assumption that, as for the case of solid friction, the fluid friction force was proportional to the pressure. Finally, Lagrange’s memoir on the theory of fluid motion of 1781 is presented as a sequel to these first theoretical constructions.
Keywords:
History of Fluid Mechanics, First Theories Applied to Fluid Flow, Torricelli’s Law, Bernoulli’s Law

1. Introduction
Since Newton (1642-1727) in the middle of the 17th century, fluid mechanics emerged as science as part of mechanics, whereas since antiquity and until the middle of the 18th century, hydraulics was mainly an activity of practitioners, and as such, could not be considered as a science in the modern sense. It was associated with an activity concerned with the motion of water, an art of channeling, raising and handling it for the different requirements of daily life. By the middle of the 18th century, mathematicians or geometers, as they were often called at the time, gave the name hydrodynamics to the science of internal and external fluid motion in general, and reserved the name hydraulics for applied activities related to the motions of water. It was possible to say that at that time hydraulics was concerned with the practical and hydrodynamics with the theoretical aspects of the same subject.
The term hydrostatics, which today is reserved for the study of liquids at rest, was then often also associated with hydraulics, up to the point that Daniel Bernoulli (1700-1782) gave the following title to the 12th chapter of his 1738 Hydrodynamics book (Bernoulli, 1968a) “Which Shows the Statics of Moving Fluids, Which I Call Hydraulico-Statics”. This book is in fact mainly concerned with the problem of water discharge from reservoirs through conduits, which can be considered as a typical hydraulic subject. This nomenclature was adopted by Johann Bernoulli (1667-1748), which entertained the same subject of the discharge in his 1743 Hydraulics book (Bernoulli, 1968b) . Since this book was in direct competition with that of his son D. Bernoulli, he had, of course, to give to it a different title, but revealing that he was treating essentially the same subject, however, using his own nomenclature and symbology based on his own principles and points of view.
Nowadays, fluid mechanics problems can be classified in internal and external flows, being the former, related to formulations that allow the calculation of flow parameters such as flow-rate and pressure in conduits and vessels, and the latter, the calculation of pressure forces that arise in bodies immersed in fluids. Calero (2008) called them “the problem of discharge”1 and “the problem of resistance”, respectively, and this seemed to be a convenient historical divide for the purpose of the present work of revisiting the theoretical developments related to the problem of discharge, in the second half of the 18th century.
The problem of discharge was also dealt with by Jean le Rond D’Alembert (1717-1783) in his book of 1744 (D’Alembert, 1744) , although this author was more famous for having dealt with the problem of resistance in his book of 1752 (D’Alembert, 1752) , which was concerned to the forces that external flows exerted on bodies immersed in fluids, and traced the origin of the famous D’Alembert paradox.
The developments then made were chosen because it was during that time that the first analytical approaches (theoretical constructions) to the problem of discharge were to appear, proposed by the aforementioned authors, namely the Bernoullis and D’Alembert, and also by Leonard Euler (1707-1783), in his 1754 paper (Euler, 1754) . According to Truesdell (1955: p. XLV) , this work may also contain the first solution of a theoretical design problem in engineering (hydraulics), as we shall see later on in the present work.
As we know, discharge problems can be solved nowadays by invoking the fluid mechanics equations of continuity, momentum and energy. Although the equivalent of the equation of continuity was longer known even at that time, the concept of mechanical energy and its conservation was not. By the end of the 17th century and the beginning of the 18th century, the conservation of vis viva (“living force”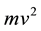 , akin to kinetic energy) and conservation of momentum
, akin to kinetic energy) and conservation of momentum
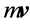 were mechanical principles under debate and not unanimously accepted by the savants of the time. Therefore, those involved in such undertaking who do not embrace such principles, have to find their own substitutes to undergird a Theory and to struggle in their approaches, which make most of the developments to be presented here rather hard to follow by the modern reader.
were mechanical principles under debate and not unanimously accepted by the savants of the time. Therefore, those involved in such undertaking who do not embrace such principles, have to find their own substitutes to undergird a Theory and to struggle in their approaches, which make most of the developments to be presented here rather hard to follow by the modern reader.
In the 17th century, body collisions were the main pattern of development of mathematical physics. Perhaps the most prominent author in this area was Huygens (1629-1695) who in 1669 submitted to the Royal Society a paper summarizing without proof rules of motion in the impact of bodies, which was printed in both the Philosophical Transactions and in the Journal de Sçavans (letter of March 18) of the same year
(Huygens, 1669)
. Both the papers were excerpted from a work largely complete by 1656 but not published until 1703 after Huygens death, De Motu Corporum ex Percussione
(Huygens, 1929)
. In these summaries, Huygens formulated seven rules for bodies whose sizes were to be estimated by their weights, which behaved as did elastic bodies. The conservation of momentum
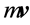 appears as rule 5, and the conservation of
appears as rule 5, and the conservation of
 appears as rule 6. In asserting this rule, Huygens did not apply it beyond the relative motion of bodies. It was Leibniz’s contribution to interpret this quantity as a measure of an “absolute”, existing in the universe as a measure of “force” (differing from Newton’s idea of force), which started the so-called vis viva controversy with a publication by Leibniz (1646- 1716) on the subject in 1686
(Iltis, 1971)
.
appears as rule 6. In asserting this rule, Huygens did not apply it beyond the relative motion of bodies. It was Leibniz’s contribution to interpret this quantity as a measure of an “absolute”, existing in the universe as a measure of “force” (differing from Newton’s idea of force), which started the so-called vis viva controversy with a publication by Leibniz (1646- 1716) on the subject in 1686
(Iltis, 1971)
.
In the posthumous work, De Motu Corporum ex Percussione, Huygens had developed a more detailed theory of percussion, in which thirteen propositions were developed. In Proposition IV, Huygens shows that the relative velocities of the bodies before and after collision are the same; in Proposition VI, he refutes Descartes’ conservation of quantity of motion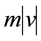 . In Proposition VIII, Huygens uses the
. In Proposition VIII, Huygens uses the
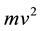 principle later known as living force relating the heights of fall to the velocities acquire, and by introducing the concept of a common center of gravity that cannot be raised, he shows that “…. When two bodies of which the velocities are inversely proportional to their sizes meet from opposite sides, each will rebound with the same velocity with which it approached”. The principle of the living force of a body and its relation to that body’s distance of fall were used by Leibniz in the demonstrations which initiated the controversy.
principle later known as living force relating the heights of fall to the velocities acquire, and by introducing the concept of a common center of gravity that cannot be raised, he shows that “…. When two bodies of which the velocities are inversely proportional to their sizes meet from opposite sides, each will rebound with the same velocity with which it approached”. The principle of the living force of a body and its relation to that body’s distance of fall were used by Leibniz in the demonstrations which initiated the controversy.
Huygens also used the conservation of the living forces in his derivation of the law of the compound-pendulum in the Horologium Oscillatorium (Huygens, 1673) , where he showed in Proposition IV that “…. If a pendulum composed of several weights and released from rest were to traverse some part of its complete oscillation, and then its individual weights were imagined, under release from the common constraint, to convert their acquired speeds upward and to ascend as far as they can, when this has occurred, the center of gravity composed of all of them will have returned to the same height that it had before the oscillation began”.
In Proposition V, Huygens states the law of the compound-pendulum: “….Given a pendulum composed of any number of weights, if the individual weights are multiplied by the squares of their distances from the axis of oscillation, and the sum of the products is divided by the product of the sum of the weights times the distance of the center of gravity of all of them from the same axis of oscillation, the result is the length of a simple pendulum isochronous with the composite pendulum, or the distance between the axis and the center of oscillation of the composite pendulum itself”. Darrigol (2005: pp. 4-15) saw a pervasiveness of the compound-pendulum analogy in the works of the Bernoullis and D’Alembert, and this would be pointed out in due course on the detailed discussions of the developments of these authors.
2. First Theoretical Constructions
All that was available as a principle for fluids in motion in vessels by the middle of the 18th century was Torricelli’s law, which can be considered the first and the simplest problem of discharge. This law, derived by Torricelli in 1644 (Torricelli, 1644) , allows the determination of the jet velocity through an orifice, made at the wall of a vessel containing water at a known level. It was established from experimental observations by Torricelli, to which he applied Galileo’s universal law on free-falling bodies, and because of that, it can be considered as a theoretical construction.
The more elaborated discharge problem with a pipe connected to a water reservoir was treated by D. Bernoulli in 1738 (Bernoulli, 1968a: pp. 291-296) , which resulted in the relationship between velocity and pressure, known as the Bernoulli law.
Later on, in 1743, J. Bernoulli (Bernoulli, 1968b: pp. 391-401) considered the more general problem of non- stationary flows through pipes of varying cross-sections2, a problem also considered by D’Alembert in 1744. As a matter of fact, the non-stationary flow formulation was proposed by D. Bernoulli as well, as we shall see later on in this paper.
In 1754, Euler (1754) presented the complete theory of a one-cylinder pump to deliver water through a piping system to an elevated reservoir, with a revolutionary and simple formulation. He complements his contribution to the discharge problem with a publication3, read in 1751, in which he presents a first attempt at a theory of the friction of fluids in piping systems (Euler, 1761) .
These works can be considered the main core of the first theoretical constructions to the problem of discharge, and will be revisited by considering the principles upon which the formulations were derived, the applications envisaged by these authors, followed by a discussion of these developments from the knowledge that we have today on the subject.
2.1. Torricelli’s Law
In 1644, Evangelista Torricelli (1608-1647) published the book Opera Geometrica (Torricelli, 1644) , divided essentially into three sections: the first De sphaera et solidis sphaeralibus; the second containing De motu gravium naturaliter descendentium et projectorum (text dedicated to Galileo) and the third section on De dimensione parabolae. In De motu projectorum, Torricelli dedicates a chapter to the motion of water (Torricelli, 1644: pp. 191-203) . This chapter was considered so important that Ernst Mach proclaimed Torricelli the founder of hydrodynamics (Mach, 1919: p. 402) . In this chapter, Torricelli’s goal was to determine the velocity of efflux of a jet of water, issuing from a small hole in a container. By experiment it was noted that when the jet is directed upward, it reaches a height less than the liquid level in the container (see Figure 1). However, he assumed that if there was no resistance to the movement, the jet would reach the same height. Starting from this hypothesis, equivalent to the principle of conservation of mechanical energy, he deduced what is known today as the Torricelli’s law: ‘The speed of a jet at a point is equal to efflux of a single drop of liquid would have if it could fall freely in the vacuum from the liquid level above the orifice’. Torricelli also showed that if the hole is made in the wall of a container, the fluid jet will have a parabolic shape. He then closes the paragraph with interesting observations of the flow breaking into droplets and the effects of air resistance.
Torricelli expressed the square root of the height law using geometrical constructions and mathematically precise words, adhering to the standards of the day (it remained for others to re-express the law in algebraic terms). Referring to the water exiting from lateral orifices in a tank and based on Figure 2, he states that the relation of the quantity of water coming out of equal apertures are under the square root of the ratio of the sublimi-
ties4, or of their heights. That is:
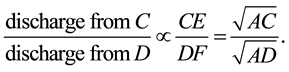 This result can be translated to:
This result can be translated to:
Figure 1. Torricelli’s schematics of an upward jet issuing from an orifice in a horizontal pipe connected to the bottom of a container (a reproduction from Torricelli’s De Motv Aqvarvm).
Figure 2. Torricelli’s geometric association of the parabola with the water exiting from lateral orifices in different heights in a tank (a reproduction from Torricelli’s De Motv Aqvarvm).
 , (1)
, (1)
where v is the velocity of the water exiting the orifice and h is the water height above the orifice5.
As was common in those days, mathematical expressions involving physical quantities were not written out explicitly, being the deductions, as we saw above, often based on Euclidean geometrical reasoning, in which proportions and equivalent lengths were related to physical parameters. Because of that, no concern would arise for the adoption of a system of units consistent with the physical quantities being addressed. This is the case of the law proposed by Torricelli, in which the quantity 2 g (where g is the gravity), once included under the square root sign, transforms this law into its present day form:
 . (2)
. (2)
According to Darrigol (2005: p. 5) , the concept of dimensional quantities would emerge only at the turn of the nineteenth century, and found its first systematic formulation in Fourier’s theory of heat.
2.2. Proofs, Disproofs and the Demonstrations of Torricelli’s Law by Reason
As show by Calero (2008: Part II, Chapter 6) and Blay (2007) , Torricelli’s law was a subject that occupied the minds of many figures before and after Torricelli. Before Torricelli, Blay shows that father Mersenne (1588- 1648) had stated Torricelli’s law in the Harmonie universelle (Paris, 1636), and concludes that, no later than 1643, not only father Mersenne but also Decartes (Blay, 2007: pp. 26-30) , the first more a experimenter, the other more a theoretician, had obtained the same law proclaimed by Torricelli in 1644.
Torricelli’s law implies two hypotheses: that the velocity is proportional to the square root of the height, and that this velocity is the same that a heavy body acquires by falling from a height equal to that from the free-surface of the water in the vessel to the orifice. Blay shows that father Mersenne could have demonstrated the first hypothesis of Torricelli’s law from experimental results
(Blay, 2007: pp. 18-19)
. To this end, he reproduces in his book a table containing the experimental results of father Mersenne (see Figure 3), in which the first column lists the eight equal parts of a vessel, and the second column lists the time in seconds that it takes to empty each part by an orifice at the bottom of the vessel. Here, by assuming that each exit velocity
 through the orifice is proportional to the respective height
through the orifice is proportional to the respective height
 of the water in the vessel, raised to the power n, that is
of the water in the vessel, raised to the power n, that is , it can be shown that the relation between the time
, it can be shown that the relation between the time
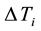 to empty the
to empty the
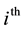 -part to its respective height
-part to its respective height



data that gives

Figure 3. A curve fitting (to the right) of Mersenne’s experimental data of 1636 [table to the left (Blay, 2007: p. 18) ] revealing that the time that it takes to empty each equal part of a vessel is inversely proportional to approximately the square-root of its respective height.
It should be noted that the results of father Mersenne only give support to the exit velocity being under the square-root of the height, and not that this velocity would be capable of rising the jet back to this height; that is, he is not stating Toricelli’s law in “full”.
Although, as we saw above, it is rather easy to experimentally verify that the velocity is under the square-root of the height, the exit velocity being equal to the velocity acquired by a heavy body falling from this height is not, because it is strongly dependent on the particular experimental conditions. Therefore, as Calero proposes
(Calero, 2008: p. 275)
, the jet velocity would be more adequately described by

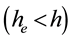

By revisiting the experimental data of Mariotte (1686), Guglielmini (1690), and Poleni (1717, 1718),
Calero (2008: pp. 275-283)
confirmed from the experimental data of these authors, the proportionality between the velocity and the square root of the height, but not that this velocity would be equal to the fall of a heavy body from this height. Further analysis of these experimental data, allowed Calero to conclude that the jet velocity was that corresponding to equivalents heights of:




Torricelli’s law is not easy to accept because since it is based in the law of free-falling bodies, which predicts that a heavy body accelerates as it falls down, why the water does not accelerate inside the vessel as it moves from the upper surface to the orifice in the bottom of the vessel? As Blay shows (Blay, 2007: p. 124) , this was exactly the proposal Varignon in 1695 “…. to examine what happens inside a conduit while the waters flows; it appears to me that the water being contiguous inside all its length, such that above it descends as fast as below; and by what consequence it does not had none acceleration inside the conduit”. After an attempt by Varignon to justify Torricelli’s law by the weight of the water column above the orifice, by 1703, he considers that the proof of Torricelli’s law “by reason alone” would be jointly from the axiom to which “the causes are always proportional to theirs effects”, from the principles of mechanics and from the general laws of motion. He thus attributed to mechanics a demonstrative perfection identical to that attributed to the Euclidean geometry (Blay, 2007: p. 130) . As we shall see later on, the deduction of Torricelli’s law “by reason alone” had to wait the works of D. Bernoulli in 1738 and J. Bernoulli in 1743.
We cannot close this section without considering the works of Newton on the subject. As shown by
Blay (2007: pp. 142-150)
, in the first edition of the Principia (1687), Newton had demonstrated that the outlet velocity of the fluid was equal to the fall of a heavy body from half the depth―a counterdemonstration of Torriceli’s law by reason. The half-depth rule had been experimentally confirmed by the experiments of Edmund Halley, between 1691 and 1692, at the Royal Society, by Roger Cotes, the editor of the 2nd edition of the Principia (1713), who in 1710, had also experimentally confirmed the conclusion of Mariotte in favor of the half-depth rule. However, by 1710/1711, Newton had reconciled with Torricelli’s law with the notion of vena-contracta, which arises from the composition of the vertical motion with the horizontal motion of the water as it flows through the orifice, in the famous cataract flow-model. The vena-contracta is a result of the convergence of the flow stream-lines after the orifice, accompany by a constriction of the flow area, which accelerates the flow from



continued to be given by


2.3. Bernoulli’s Law
In 1738, Daniel Bernoulli published the book Hydrodynamics (Bernoulli, 1968a) , in thirteenth chapters. In the 12th chapter, with the title: Which shows the Statics of Moving-Fluids, which I call Hydraulico-Statics, D. Bernoulli proposes:
“§1. …. To go beyond the common rules of hydrostatics by considering the statics of fluids which are moved within vessels such as of water flowing through conduits to leaping fountains…, those who have spoken about the pressure of water flowing through aqueducts and the strength required of the latter for sustain that pressure did not hand down any laws other than those for extended fluids with no motion…”
“§2. It is singular in this hydraulico-statics that the pressure of water cannot be defined unless the motion has been known correctly…”
Firstly, from these quotations, it is clear, as it was already mentioned before, that there is a preoccupation in giving a proper denomination for the new area of study which he is venturing at, and secondly, that he is essentially seeking a relation between pressure and velocity for flows within conduits. As we will see, the relation thus derived is nothing more than Bernoulli’s law.
The pervasiveness of the compound-pendulum analogy is clearly seen in the work of D. Bernoulli, who adapted Huygens’s Proposition IV of the Horologium Oscillatorium (Huygens, 1673) to the problem of discharge in the following form:
“… If any number of weights begin to be moved in some way by the force of their own gravity, the velocities of the individual weights everywhere will be such that the products gathered from the squares of these velocities multiplied by their appropriate masses are proportional to the vertical height through which the center of gravity of the composite bodies descends multiplied by the masses of all of them…”
The equality between potential ascent and actual descent, a nomenclature also used by Huygens in Part 4 of the Horologium Oscillatorium (Huygens, 1673) , was defined by D. Bernoulli as follows:
“… The potential ascent of a System, the individual portions of which are moved at any velocity whatever, indicates the vertical height to which the center of gravity of that System reaches if the individual particles, their motion having been turned upward with the proper velocity, are understood to ascend as far as they can; and actual descent denotes the vertical height through which the center of gravity descends after the individual particles have come to rest…”; which is recognized as the modern equivalent to the principle of conservation of mechanical energy.
This principle, together with the principle of conservation of the living forces were applied by D. Bernoulli in various developments contained in Hydrodynamics. For instance, in §8 of the Third Chapter, by applying the equality between potential ascent and actual descent, D. Bernoulli develops a general expression for the motion of a homogeneous fluid flowing out of a given vessel through a given orifice in the form

which is very small, then
However, what is considered the most important development in Hydrodynamics appears in §5 of the Twelfth Chapter in the attempt to relate pressure and velocity, from where Bernoulli’s law supposedly had emerged.
The basis for this development is Figure 4, where D. Bernoulli assumes that the pressure at the horizontal pipe wall is proportional to the acceleration that the water in the pipe would receive if the entire obstacle to motion would vanish, so that the water might be ejected instantly into the air; “… The pressure of the water against the walls of the pipe ED is sought…”
Considering that the pipe ED is suddenly broken at cd. The “particle” ac, infinitely small and about to flow is indicated by




element



Since to D. Bernoulli, pressure is proportional to acceleration, the increment in velocity



Figure 4. The discharge from a tank through a horizontal pipe, from which Bernoulli’s law was derived (a reproduction from Hydrodynamics).
sure at the pipe wall, hence the pressure is proportional to
At the instant when the pipe is broken,
ricelli’s law for the velocity in the orifice






fice is closed

Since



“… It is not difficult to anticipate the laws of this hydraulico-statics if both the shape of the vessel and the velocity of the water flowing through the conduits are assumed at will as anything whatever. Indeed, the pressure of the water will always be
The result:

became known as Bernoulli’s law. Surprisingly, Equation (3) does not resemble the usual form in which this equation is written.
Two comments can be made related to D. Bernoulli’s approach to the problem of discharge.
1) When the conservation of mechanical energy is applied to D. Bernoulli’s flow model (with the kinetic energy written as




2) As
Truesdell (1955: p. XXVIII)
pointed out: “… all appearances to the contrary,

This is because v is a known constant and independent of x and,


finite increments. Therefore,



because the first term has units of pressure, whereas the second term has units of acceleration. However, this proportionality can be turned out dimensionally homogeneous by dividing the pressure p in the first term, by the mass of the water per unit of cross sectional area of the pipe


which is a more familiar expression for Bernoulli’s law. It is seen that by a rather tortuous path and with some fixes, Bernoulli’s equation as it is known in the present-day, could be recovered from the Bernoulli’s rather precarious flow model for the problem of discharge.
A final note to D. Bernoulli’s is that he develops the relation between pressure and velocity in terms of the pressure against the wall of the pipe, which lead historians of fluid mechanics to believe that he did not have the concept of internal pressure of the fluid. This supposition must be seen with care because in §5 of the twelfth chapter of Hydrodynamics, D. Bernoulli considers that if the base FD were missing (see Figure 4):
“… The water in the pipe tends to a great motion, but its pressure is impeded by the added base FD. By this pressure and repressure the water is compressed, which very compression is confined by the walls of the pipe, and hence these sustain a like pressure…”
From these remarks, it seems that Bernoulli indeed conceive that the water itself was responsible for transmitting the pressure to the pipe walls, and hence he might have realized that this transmission would occur internally, from one ‘drop’ of water to the other. Moreover, D. Bernoulli was known for using the piezometer (liquid column manometer) consisting in sticking glass tubes in small openings in pipes or in human arteries (D. Bernoulli was trained as a doctor) to measure the wall pressure. Since he was considered a great experimenter, one can imagine he sticking the tube on the core of the flow, on purpose driven by curiosity or even by accident, and realizing that the elevation of the liquid (water or blood) in the tube, no matter in the core or in the walls (of the pipe or the arteries), was the same. It seems that there are other reasons for not reasoning in terms of internal pressure in his developments.
1) Perhaps he was more concerned with practical aspects related to the strength of the walls of aqueducts to sustain pressure (§1, chapter twelfth of Hydrodynamics):
“… those who have spoken about the pressure of water flowing through aqueducts and the strength required of the latter for sustaining that pressure did not hand down any laws other than those for extended fluids with no motion. …”.
2) As we saw, the way that he equates his flow model of discharge, is different from the one used nowadays, in which the balance of forces is applied on an infinitesimal fluid element between any two cross-sections of the conduit, in which the internal pressure forces acting on these cross-sections would have to be taken into account. However, this approach had to wait Euler’s developments in 1754. So, it is here conjectured that he had no need to consider the internal pressure of the fluid in his developments, rather than not having its concept.
The publication of Hydrodynamics was an immediate success, which have raised envious criticisms of two great geometers of that time: his own father Johann Bernoulli, and D’Alembert. The works of both contenders will now be revisited.
2.4. Johann Bernoulli’s Approach
In 1743, the book Hydraulics (Bernoulli, 1968b) authored by Johann Bernoulli appeared in print, pre-dated 1732. A lot of controversy was involved with this publication. For a more detailed account on the dispute on dates etc., see the preface by Hunter Rouse to the translated version of Hydrodynamics & Hydraulics, from which this excerpt was taken, regarding the claims on priority:
“… There is no record that Johann had written anything whatever on the subject of hydraulics until some months after his son’s treatise was off the press, when he stated in a letter to Euler that he was preparing a manuscript on hydraulics which was already well along. Nevertheless, he indicated in the first part that it was written in 1732, a full year ahead of the Russian version of his son’s! The second part followed the first to St. Petersburg in 1740, and the two were eventually published, as Johann had requested, in the Memoirs of the Imperial Academy of Science for 1737 and 1738 (which were printed, respectively, in 1744 and 1747). They actually first appeared in his collected works, published in 1743…”
In a letter from Euler to J. Bernoulli about the book, which was quoted in part in the foreword to the Swiss version of Hydraulics (with J. Bernoulli calling Euler ‘Most Sagacious Mathematician’), allows one to grasp, in Euler’s view, the contribution of J. Bernoulli over that of D. Bernoulli:
“… Your very renowned Son, who, however, defined pressure in a rather indirect manner only so far as the entire motion has already acquired the steady state, nevertheless, after the genuine method had been brought to light, You at once determined most accurately the pressure in every state of water, because of which Your most praiseworthy discovery I congratulate You from my heart…”
In 1743, D. Bernoulli wrote a letter to Euler, from which this quote is taken:
“… Your Excellence says that I have determined the pressure of fluids flowing through a conduit in no other way than for the steady state, whereas I show immediately on page 259 toward the bottom that generally the
pressure is
We shall now see what J. Bernoulli has done for the problem of discharge.
In the Preface of Hydraulics, J. Bernoulli claimed that the science of hydraulics has not been subjected to the laws of Mechanics, being the developments so far based on experience and theories that were uncertain, and with insufficient foundation, particularly the conservation of living forces, which he recognized as certainly true, and proven by him himself, but that still were not accepted by all philosophers. For him, the true foundations of hydraulics ought to be the principles of mechanics, namely Newton’s principles.
From Newton’s concept of an accelerative force impressed on a body, which is responsible for the velocity
acquired by the body in the traveled space, J. Bernoulli wrote
result’. This result is recognized as the work done by a variable motive force p acting on a body of mass travelling a distance x being equal to the variation of the body kinetic energy. This and translated gravitation are the most significant of the eleven lemmata introduced by J. Bernoulli in the Preface of Hydraulics.
J. Bernoulli calls translated gravitation, the force from the lower regions that are translated to the uppermost surface of the water contained in a vessel, which constitute the total immaterial motive force by which all the water in the vessel is pressed downward. For the modern reader, this translation resembles Pascal’s principle, which says that the pressure applied to any point of a fluid at rest is transmitted to the entire fluid. In fact, according to J. Bernoulli, if a stratum of water from the lower regions of the vessel has an area m and a weight
the translated gravitation to the uppermost surface will be
According to Calero (2008: p. 329) , J. Bernoulli does not identify pressure as force per unit of area; hence, the necessity of this force translation rule.
Darrigol sees here another pervasiveness of the compound-pendulum analogy (Darrigol, 2005: pp. 9-10) , in which forces at any point of a system are replaced by equivalent forces at a particular point of the system. This can be traced to an earlier work by J. Bernoulli (Bernoulli, 1714: pp. 168-186) on the nature of the center of oscillation, in which he confirms Huygens’s Proposition V, Part 4 of the Horologium Oscillatorium (Huygens, 1673) , using the law of the levers, in which forces that have the same moment have the same effect.
From the Preface on, Hydraulics is divided in two parts: the first part is concerned with the motion of water through vessels and cylindrical conduits, and the second part contains a ‘direct and universal method for solving all hydraulics problems’. In the first part, one finds J. Bernoulli derivation of Bernoulli’s law, and in the second part, the derivation of a general expression for not necessarily steady flow in pipes of any form, which forms the basis of the remaining work.
In Section VIII, Part 1 of Hydraulics, J. Bernoulli considers the ‘crux of the whole matter’ for finding the law of acceleration according to which the liquid flows through a conduit; that is, the determination of the motive force which acts ‘in the throat necessary to change the lesser velocity to the greater’. J. Bernoulli defines the throat as the region right after the contraction enclosed by the curve IMF on the top and the length HG on the bottom (see Figure 5). The motive force p (per unit of density) is responsible for accelerating the water as it passes through the throat from the larger area h to the smaller area of the conduit. From these considerations, he deduces that:

where v is the velocity in the conduit after the contraction.
Since this result was obtained for a liquid with unit density, then for a liquid with a general density
former expression can be re-written as
the upstream cross section area h is in fact the pressure that accelerates the water through the throat; it is actually the pressure differential


where the indices 1 and 2 refers to the conditions upstream and downstream of the throat, respectively. The continuity relation

In Section X, Part 1 of Hydraulics, J. Bernoulli considers a vertical cylindrical vessel with area h, conti-
Figure 5. Horizontal pipe with a contraction (throat) used by J. Bernoulli to derive Bernoulli’s law (a reproduction from Hydraulics).
nuously full of water at a height a, and with an horizontal cylindrical conduit with area m connected at its base. For this case, and by substituting in Equation (5) p for , where g is the gravity, and considering that


area m of the conduit is very small,


In Sections II?VIII, Part 2 of Hydraulics, J. Bernoulli develops a general expression for the non-stationary velocity of a liquid flowing out of a conduit of any shape, which may be inclined differently in its different parts (see Figure 6). The approach taken consists on finding the motive force responsible for maintaining a steady flow through the conduit of any shape, and the motive force responsible for the non-steady flow behavior. J. Bernoulli called the latter hydrostatic force and the former hydraulic force. These forces are responsible for what is known today as the convective acceleration and the local acceleration, respectively.
In Section IV of Hydraulics, the hydrostatic force―the force responsible for the convective acceleration― was obtained by translating the effects of vertical motive force from an elementary intermediate layer, given by for the layer Fm with the area , to the first area h at the top of the conduit, resulting in the equivalent
ing from the last layer, with the area w and velocity v, to the top layer, with the velocity



vertical, at the bottom and at the top of the conduit, respectively. This is the hydrostatic force, and accounts the required motive force to accelerate the liquid as the area of the conduit changes from h at the top to w at the bottom. This force is responsible for what is known today as the convective acceleration.
Since in this case the gravitation force is the only motive force available, by translating the elementary gravitation forces (per unit of density) of the elementary layers to the first area h, and upon integration through the total height



Figure 6. Conduit used by J. Bernoulli to derive a general expression for the non-stationary velocity of a liquid flowing out (a reproduction from Hydraulics).
If we contrast this result for



head is the opposite of the velocity head as the relation between the flow areas at the top and at the bottom changes, which is the essence of Bernoulli’s law.
In Section V of Hydraulics, the hydraulic force―the force responsible for the local acceleration―was equated by J. Bernoulli as follows. The displacement of the layer Fm when the elementary displacement at the
exit is



segment

tical motive force of this layer, translated to the first area h gives the equivalent
integration through the total length of the axis of the conduit, for any layer and for any acquired velocity v, noting
that herein not only h and w but also


draulic force, and accounts the required motive force for the actual acceleration of the liquid flowing out. This force is responsible for what is known today as the local acceleration.
When the gravitation force

for a liquid with unity density, claiming that this is the most general equation for the determination of the veloc
ity with which the liquid flows out at any moment. It is understood that


geometry of the conduit under consideration.
Based on this general equation, J. Bernoulli shows with a numerical example that the transit time from rest to the steady state efflux, from rather wide vessels through narrow orifices is imperceptible, and can safely be considered constant. This is an interesting conclusion regarding the importance of the hydraulic force in such problems.
The remaining of Part II, is basically dedicated to other applications of the general equation in problems such as: the derivation of an expression for the pressure at the walls of the conduit (Sections XI & XII), the variation of the exit velocity during the emptying of vessels (Sections LI & LII)―to be seen in more details later on in the present work, the making of clepsydras (Sections LIV?LIX), the examination of Newton’s cataract (Section LX) etc.
In Section VII, Part 2 of Hydraulics, J. Bernoulli’s writes6

6Here we find a rare instance of a precise quotation of Torricelli’s law as is known today:
where
Equation (9), for the case where

In Section X, Part 2, we also find for the first time the interpretation of internal pressure―called immaterial force by J. Bernoulli―:
“… in portions of fluid acting mutually on each other, the immaterial force lying between must be considered just as elastic air, which extends itself not only to opposite directions, but also into all surrounding regions; from which now it is easily understood that from this immaterial force itself the pressure, which is the subject here, develops. This certainly is exerted on the walls of a conduit, by which in turn it must be confined while it acts freely forward and backward on the portions of the liquid wherein it exists…”
J. Bernoulli approaches can be considered remarkable for the time for the following reasons.
1) For reaching the same law proposed by his son D. Bernoulli for steady sate flow with a physical model more attached to reality, that is, from the pressure developed for accelerating the fluid in the contraction of a conduit.
2) For writing expressions with dimensionally homogeneous quantities (such as Torricelli’s law), which were not the standard of the day.
3) For giving for the first time the correct interpretation for the internal pressure in a fluid.
For these reasons, his contributions to the problem of discharge can be considered far superior than that of D. Bernoulli, and he would naturally have deserved a place in the hall of the greatest contributors to fluid mechanics, and particularly to the problem of discharge, without the need to compete with his son for pioneering the work in the area. Therefore, it is not appropriate to say that J. Bernoulli predated the work of D. Bernoulli; what in fact might had happen, is that after the publication of Hydrodynamics he saw that he had missed a great opportunity to be the pioneer in an area where he felt he had better approaches than those of his son’s, perhaps since an earlier time than that when Hydrodynamics appeared. As mentioned earlier, the superiority of J. Bernoulli approach to the problem of discharge over that of D. Bernoulli was even recognized by Euler. Unfortunately for Johann, Bernoulli’s law was named after Daniel.
2.5. D’Alembert’s Approach
In the Preface of the Traité de l’ équilibre et du mouvement des fluides (D’Alembert, 1744) , D’Alembert makes remarks to some results and approaches used by D. Bernoulli in Hydrodynamics. For example, he judged that the application of the principle of conservation of living forces, considering the fluid particles as elastic corpuscles was an induction without force, and that it was in need of a more clear and exact demonstration. He claims that despite the fact that this was already done by him in his Traité de Dynamique (D’Alembert, 1743) , he would prove it again in a more extended and detailed form.
In a letter to Euler of July 7, 1745, D. Bernoulli of d’Alembert’s work says (see Truesdell, 1955: p. XXXVII, footnote 2 ):
“… I have seen with astonishment that apart from a few little things there is nothing to be seen in his hydrodynamics but an impertinent conceit. His criticisms are puerile indeed, and show that he is no remarkable man, but also that he never will be…”
Therefore, if D’Alembert was to produce something new and meaningful, of course he could not follow D. Bernoulli’s footsteps, at least as far as mechanical principles are concerned. In the Traité de Dynamique
(D’Alembert, 1743: pp. 50-51)
, a “general principle” comes in the form of a “general problem”, in which D’Alembert proposes to find the motion that each body should take in a system of bodies arranged mutually in any manner whatever; in which a particular motion is impressed on each of the bodies, that it cannot follow because of the action of the others. For finding the motion of the several bodies the following principle is given: “Decompose the motions a, b, c, etc. impressed on each body into two others,




If one denotes ma an applied force on the mass point m of a connected system, and



librium of a system of N point masses


system of particles such as a fluid, the integral form of these summation expressions are used by D’Alembert in the Traité de l’ équilibre et du mouvement des fluides.
A theorem presented by D’Alembert in §22 of the Traité de l’ équilibre et du mouvement des fluides (D’Alembert, 1744) , which is a geometric interpretation of his dynamic principle, forms the basis of the various developments presented in this Traité. By dividing the vessel to the right of Figure 7 into horizontal layers (tranches), each one submitted to a particular accelerative force represented in the left side of this figure (not necessarily the gravitational force), he says that ‘the fluid in such state cannot be in equilibrium, unless the area is not zero; that is, the sum of the positive areas equals the sum of the negatives.’
In §25 of the Traité de l’ équilibre et du mouvement des fluides
(D’Alembert, 1744)
, by calling

that









second law for the equilibrium.
D’Alembert had rejected the concept of force and thought of mechanics as “the science of effects, rather than the science of causes”. “… All we see distinctly in the movement of a body is that it crosses a certain space and that it employs a certain time to cross it. It is from this idea alone that one should draw all the principles of mechanics…” (D’Alembert, 1743: p. XVI) . D’Alembert was born ten years before Newton died in 1727 and Newton, in turn, was born in the year which Galileo died. According to Hankins (Hankins, 1970: pp. 152-153) , when d’Alembert’s Traité de Dynamique was published in 1743, Newton’s general laws of motion were not yet regarded as the major synthesis of all those that had gone before, up to the point that Newton is mentioned only
Figure 7. Vessel (to the right) and representation of the accelerative force (to the left) for the presentation of the fluid state of equilibrium (a reproduction of Figure 8 from the Traité de l’ équilibre et du mouvement des fluides).
three times in the Traité de Dynamique, and not associated with any important principles. The search for mechanical principles continued, particularly with d’Alembert, who rejected “obscure and metaphysical” entities― particularly “forces” and “motive causes”. This is way the expression
In the remaining of Book I of the Traité de l’ équilibre et du mouvement des fluides, D’Alembert discuss various cases o fluid equilibrium such as: fluid equilibrium with solids in it, pressure distribution in the fluid layers with gravity in a constant direction, equilibrium of fluids of different densities, law between gravity and density in different layers of a fluid with constant gravity in a given direction, equilibrium of a fluid where the layers vary in any way in gravity and density, “adherence” of fluids, equilibrium of a fluid with a curved upper surface (figure of the earth), the equilibrium of elastic fluids (various cases).
I will now focus on some paragraphs at the beginning of Book II of the Traité de l’ équilibre et du mouvement des fluides, entitled “On the Movement of Fluids Encircle in Vessels”. After have beginning Chapter I demonstrating two theorems, in §86 D’Alembert remarks that “it is evident that the fluid will remain in equilibrium, if each layer is not animated by an infinitesimally small velocity
Before presenting the case “Movement of a portion of a fluid without weight inside an indefinite vessel”, d’Alembert presents as preparation, a vessel of any shape (to the left of Figure 8), and defines a corresponding curve (to the right of Figure 8), constructed in such way that, as for example, the intermediate YX, is given by

which is given by the integral

layer, for which the product



In §90, D’Alembert poses Problem I as follows: “… Suppose that a given quantity of Fluid CDLP (Figure 32) homogeneous and without weight, is put into movement by any cause such as by the impulsion of a piston, which moves according to AB inside an undefined vessel; it is required to find the velocity of this Fluid in each
Figure 8. Vessel (to the left) and representation of a curve given by

instant…” Since the velocity of the layer CD is given by

it’s possible to find all others.
D’Alembert equilibrium condition requires that





Then, the velocity in any other layer such as CD, is the same as GH to CD. Since

In §100, D’Alembert gives a solution to the problem for the fluid subjected to a gravity p. In this case, his basic expression



which, according to d’Alembert, when combined with
In §105, D’Alembert gives a solution for the velocity of the layer PL. This solution begins by rewriting Equation (13) as



In § 113, and based on Equation (14), D’Alembert gives the solution for a cylindrical vessel with an aperture made in its bottom (Figure 9), in which the water is subjected to the gravity p, as:

When PL is a very small aperture

D’Alembert claims that Equation (14) is the same found by D. Bernoulli, via the principle of living forces. Indeed, this is the same equation developed by D. Bernoulli in §8, Third Chapter of Hydrodynamics, in which it
is written as

equations are all equal to J. Bernoulli’s general non-steady flow equation [Equation (10)] as well.
7As noted before with J. Bernoulli, here appears again a precise quotation of Torricelli’s law written as

8There is an error in the second-hand side of this equation, in which


By calling
Figure 9. Vessel with an aperture made in the bottom, for which Equation (15) was developed (a reproduction of Figure 40 from the Traité de l’ équilibre et du mouvement des fluides).
reduces to
which is very small, then
In most of the developments in Book I & II of the Traité de l’ équilibre et du mouvement des fluides, D’Alembert essentially replicates problems already dealt with by Daniel and Johann Bernoulli, but using his own principles and approaches instead. He criticizes D. Bernoulli for using the principle of the conservation of living forces when the change in velocities is not infinitesimal (D’Alembert, 1744: p. 109) , where he might be wrong, particularly when D. Bernoulli breaks the pipe in the development of his law because, as we saw earlier, the conservation of living forces was derived by Huygens for elastic impacts, and the breaking of the pipe can be considered a sudden impact in the water initially at rest in the pipe. D’Alembert also saw the approaches of J. Bernoulli with some reserves. For example, he remarks that various points in the Theory of J. Bernoulli needed demonstrations, and criticizes him by using a “very complicated method’ for determining the pressure at the bottom of the vase (D’Alembert, 1744: pp. 159-160) ”.
In the Traité de l’ équilibre et du mouvement des fluides there are rare moments that d’Alembert talks about pressure, and worse, he did not seem to have realized and grasped the very important basic relation between pressure and velocity in fluid flows, as was done very explicitly by D. Bernoulli in Hydrodynamics. This is perhaps a consequence of his aversion to forces, and particularly to pressure forces. We will only find for the first time a specific development of the relation between pressure and velocity much later in his Essai d’une nouvelle théorie de la résistance des fluides (D’Alembert, 1752: p. 24) , in a result that apart from differences in nomenclature and symbology, resembles J. Bernoulli’s (Equation (5)); that is, Bernoulli’s law.
2.6. A Non-Steady Flow Application Example
The shape of the vessel is only important in non-steady flows and has a direct impact in the value of M (see Eq
uation 10), which for vessels with cross-sectional areas normal to the vertical axis is given by
x is the vertical axis and y is the cross-sectional area of the vessel at the x co-ordinate. However, in Equation (10), we see now time dependence appearing explicitly in this equation. The following application by J. Bernoulli will show how the time dependence is recovered from this equation.
The influence of the vessel shape, which appears equally in the Bernoullis and D’Alembert formulations, can be seen in the problem given by J. Bernoulli in Section XXVII, which concerns the calculation of the time that it takes for the exit velocity to reach the steady-state value from rest.
Under these conditions and for
The time differential

For cylindrical or prismatic vessels of cross-sectional area h and height a, for which
which implies an infinite time for the steady-state velocity

However, the steady-state velocity does attain 99 per cent of

As numerical examples, let’s consider:


0.01, for which the latter expression yields

These results confirm a Corollary given by J. Bernoulli in Section XXVIII of Hydraulics “… The efflux from rather wide vessels through narrow orifices can safely be considered as constant the instant after beginning of motion.”
Before closing this section, it should be pointed out that this problem forms the basis of the so-called Rigid Column Theory in hydraulic transients, in which the same expression given above for the time to reach the steady-state is simply obtained by applying Newton’s 2nd law to the water that is accelerated in a pipeline, due to the sudden opening of a valve at the end9.
3. Euler’s Contributions
Euler’s main contributions to the problem of discharge appeared almost simultaneously in two publications of 1754, namely, Sur Le mouvement de l’eau par dês tuyaux de conduit (Euler, 1754) , and Tentamen theoriae de frictione fluidorum (Euler, 1761) 10. In the former publication, Euler presents the theory of a pump delivering water through a conduit to an elevated reservoir; in the latter publication, he presents the theory for water pipe friction. I shall now present the highlights of the first publication, to later on get into more details of the second publication.
In both memoirs, Euler strategy consists in finding the accelerations necessary to perform the necessary work, and according to Newton’s second law, equates them to the forces available to perform it. In the pump memoir, since the flow is non-steady, the accelerations that come into play, in modern terms, are the local and the convective accelerations; and the forces responsible for these accelerations are the gravitational and pressure forces. In the friction memoir, he only considers the steady-state case, in which only the convective acceleration comes into play, and of course, with the additional friction force. As far as mechanical principles are concerned, Euler does not make any elaborations, and simply applies Newton’s second law quite naturally in both memoirs. The pressure forces are equate quite naturally as well, stripped from any physical or metaphysical considerations.
3.1. Euler’s Theory of Pump Delivering Water to an Elevated Reservoir
In the introduction of Sur Le mouvement de l’eau par dês tuyaux de conduite (Euler, 1754) , Euler mentions the works of the Bernoullis and D’Alembert on hydraulics, but considers their approaches “less than general” because they did not resorted to the “Analysis of infinitesimals”. Moreover, since these authors have considered the motion of water in vessels of general shapes, one would try to find in vain the application of a specific case, and the Practitioners would find even less resources to conduct their projects. He then proposes to develop this subject, “only as far as to its application in practice is concerned, which would allow finding the clarifications that are necessary”.
According to Eckert (2002) , the origins of this paper may be traced to Euler´s involvement by the request of the King of Prussia, Frederick the Great, to calculate the hydraulics for a fountain in his Park at Sanssouci in Potsdam. Euler’s involvement began in 1749, when a new effort was made in the park to improve the water- raising machinery and the tubes for the pipeline to the elevated reservoir.
Euler then presents the complete theory of a one-cylinder pump to deliver water through a piping system to an elevated reservoir (see Figure 10). Here, since the flow is non-steady, Euler first find expressions for the local and convective accelerations in a general conduit cross-section, which according to Newton’s second law, equate to accelerative forces, namely gravity and pressure. Consequently, by balancing these forces on two infinitely near cross-sections of a fluid element in a circular conduit, the following differential equation is obtained:

where p is pressure (in fact the pressure head), z and a are the diameters of the conduit and the cylinder bore, respectively, y is the height at ZY, r is the piston excursion to acquire the velocity v (in terms of sublimity), s is the co-ordinate along the conduit, and C is a constant.
According to Truesdell (1955: p. XLV) , Euler’s method is simpler and clearer, and for the first time he had interpreted the pressure force in its modern sense, as the product of pressure by the cross-sectional area. Euler’s method of balancing all forces against the accelerations is the method still in use today in any introductory course in fluid mechanics.
The memoir on pump-pipe flow gives a good idea of Euler’s methods and approaches to physical problems,
Figure 10. Euler’s sketch of a one-cylinder pump to deliver water through a piping system to an elevated reservoir [a reproduction from Sur Le mouvement de l’eau par dês tuyaux de conduite (Euler, 1754: p.148) ].
and particular to fluid flow problems. However, this can be considered a specific and more complex problem than the ones that I have considered so far. Therefore, for a fair comparison with the approaches of the other authors considered here, I shall analyze another one of Euler’s contribution, in which the flow from an elevated reservoir is driven only by gravity, but taking into account the loss of head along the conduits. This contribution appears in Tentamen theoriae de frictione fluidorum (Euler, 1761) , in which he developed a theory to estimate the loss of head along water conduits.
3.2. Euler’s Theory on Fluid Friction
Tentamen theoriae de frictione fluidorum (Euler, 1761) was built under the wrong assumption that, as for the case of solid friction, the fluid frictional force that appears at the wall of the conduit is proportional to the pressure. As turned out to be much later realized, Euler indeed did not recognized that the friction force is essentially a viscous effect, and hence independent of the applied pressure.
Euler’s developments in this paper are only for steady flow cases (see Figure 11). Here, by adopting for the fluid friction the same law as for the solid friction, by which the friction force is supposed to be proportional to the applied normal force, Euler wrote the fluid frictional force as





where contrary to the accepted symbology in fluid mechanics, v is not the velocity, but instead the sublimity, which is the height from which a heavy body would have to fall, to acquire the same velocity as the water would have at the orifice at the end of the conduit, with an area of
Equation (17), without the friction term in the second hand side, is recognized as what is now referred to the steady-state incompressible Euler’s equation for the ideal, non-viscous fluid, written in the intrinsic co-ordinate s along a streamline. As it is, Equation (17) is in non-dimensional form, with all its terms written in units of length; and, as for the kinematics with Galileo, Euler was successful in geometrizing a fluid dynamic problem as well.
It should be noted that the integration of Equation (17) without the friction term, leads to Bernoulli’s equation in the form


Figure 11. Vessel used by Euler in the formulation of his pipe wall friction theory [a reproduction of Figure 2 from Tentamen theoriae de frictione fluidorum (Euler, 1761) ].
cross-sections z and h, respectively. This is an expected result because the integration of the incompressible Euler’s equation for the ideal, non-viscous fluid along a streamline results in Bernoulli’s equation, which is considered the most appropriate formal form for the derivation of this equation.
The solution for p requires repeated integration by parts of Equation (17), in which the exponential functions that appear in the process are written as power series. Following this procedure, in §34 of Tentamen theoriae de frictione fluidorum, Euler gives the solution for p and v for a vessel of any shape, which is modeled by a composition of piecewise straight tubes as shown in Figure 12. For this vessel the following symbology applies.











Orifice

For the state of the compression the following symbology is given by Euler.
In
in
in
in
in
The pressure at these junctions are then obtained as follows.
Figure 12. Vessel made by a composition of piecewise straight tubes, which was used by Euler as a model of a vessel of any shape [a reproduction of Figure 4 from Tentamen theoriae de frictione fluidorum (Euler, 1761) ].
The exit velocity at the orifice in the end of the vessel is the given by:

where
In the case of no friction,


and for


This last result clear shows that for the case of no friction, the exit velocity for a given height q is independent of the shape of the vessel, and depends only on the first and the last flow areas.
Based on Equation (18), Euler then gives solutions for v for the following cases; Case I-vertical straight tube of uniform section; Case II-vertical straight tube composed of two parts of unequal sections; Case III-horizontal straight tube of uniform section; Case IV-inclined tube of uniform section, including a table of the gradient required before a stream of a given depth will begin to flow; Case V-inclined tube, analyzed together with a vertical tube followed by an horizontal tube with an orifice that projects water vertically.
On passing, it is interesting to note that a situation arose from Case I, discussed in §50, 51 of Tentamen theoriae de frictione fluidorum, that would occur for the case where the length of the vertical tube exceeded twice the atmospheric pressure head (of 30 ft.), when the pressure at the tube-wall would become negative, and the flow would leave behind the vacuum (i.e., cavitation). In this case, Euler points out that the calculations are no longer valid. It should be noticed that earlier, in 1738, Daniel Bernoulli in his book Hydrodynamics, and in 1744, d’Alembert in his book Traité de L’Équilibre et du Mouvement des Fluides, had both anticipated the possibility of a theoretical negative wall pressure.
An analysis of Euler’s Case III without friction, allows us to recover D. Bernoulli’s results (see Figure 13).
For this case, Equation (18) for


Figure 13. Euler’s Case III-horizontal pipe with an orifice at the end, connected to a reservoir [a reproduction of Figure 7 from Tentamen theoriae de frictione fluidorum (Euler, 1761) ].
pipe would then be given by



reservoir, the pipe, and the orifice, respectively. Substituting the expression for v, we will have that in general,
the pressure in the pipe would be given by


Before closing this section, I shall discuss the result
size of f, in which case
A physical model of such situation, was given by J. Bernoulli in Section XXXIII, Part II of Hydraulics, in which a large pan of very small height is attached to the top of the vessel (see Figure 14). In this case, the height of the pan does not add to the height a of the vessel, with the water flowing into the conduit with the required velocity to maintain it constantly full.
When


4. Lagrange’s Theory of Fluid Motion
To see how was Lagrange’s approach to the problem of discharge, I need to bring first to this discussion another one of Euler’s papers, that in which the famous Euler’s equations were derived. These appeared in the Principes generaux du mouvement des fluides (Euler, 1757) . It is not the case to revisit this paper here, not only because
Figure 14. A large pan attached to the top of the vessel, used as a physical model by J. Bernoulli to justify situations where

this has already been done elsewhere12, but also because this publication does not deal directly with the problem of the discharge.
Lagrange, in a memoir of 1781 (Lagrange, 1869) , presented a theory of fluid motion, and develops a general method for the solution of discharge problems. In Part I of the memoir, Lagrange’s developments follow quite closely Euler’s steps in the above mentioned paper. However a substantial difference marks both approaches, since the Lagrangian specification of the flow field is that of looking at fluid motion where the observer follows an individual fluid parcel as it moves through space and time, whereas the Eulerian specification of the flow field focuses on specific locations in the space through which the fluid flows as time passes. The Lagrangian and Eulerian specifications of the flow field are sometimes loosely denoted as the Lagrangian and Eulerian frame of reference.
However, in general both the Lagrangian and Eulerian specification of the flow field can be applied in any observer’s frame of reference, up to the point that one finds no differences in the resulting differential equations of motion. This is so true because Lagrange’s equation of motion, developed in Part I of the memoir, is equivalent to that of multiplying Euler’s equation by an element of trajectory whose components are

where t is the time,





Here, each fluid particle has its own velocity components




Lagrange then introduces the velocity potential

which allows the determination of the pressure. This equation, together with the incompressibility equation:

allows the determination of
Before presenting Lagrange’s approach to the problem of discharge, it should be noticed that he missed the opportunity to obtain Bernoulli’s equation from Equation (21) (which unlike Euler in the Principes generaux du mouvement des fluides Lagrange did not obtained it in his memoir), by recognizing that along a streamline



which is recognized as the steady-state Bernoulli’s equation, where
In Part II of the memoir, Lagrange gives a general solution for the fluid motion in vertical vessels of any shape, by expanding the velocity potential





By just retaining the first term in the power series expansion for
Again, by retaining just the first term of the power series expansion he got an expression for the pressure as
In these expressions,




which would be determined according to particular cases.
The equation that represents the condition in which the same fluid particles would remain at the exterior surfaces of the fluid is
From these equations, which form the basis for the solution of discharge problems, Lagrange then develops specific methods for the solution of four cases of discharge; Case I-an infinite vessel in which a given quantity of fluid flows; Case II-a vessel of a given length in which the fluid flows through the bottom; Case III-an infinite vessel which is kept full at the same height by a new fluid poured in continuously; Case IV-a vessel of a given length which is kept full at the same height.
It is not the case here to go deeper into the Lagrange’s procedures for the solution of these cases, not only because their lengthy and rather complicated, but also because they all end up in integral equations, which are to be solved according to particular vessel shapes in each case; in other words, the formulations are not for the practical use. But the idea is that once these integral equations are solved, it is possible to get the x position of the upper and lower surfaces





Lagrange begins his memoir by praising the work of d’Alembert, but omits the work of Euler, which, as we saw above, he follows closely in the first part of the memoir. Through the end of the memoir, after having dealt with the problem of discharge, Lagrange found that his solutions conform to those of the first Authors, namely D. Bernoulli in Hydrodynamics, J. Bernoulli in Hydraulics, and D’Alembert in the Traité des Fluides, which have based their works on the supposition that the fluid layers maintain their parallelism as they descend through the vessel.
5. Summary and Conclusion
In a time when the laws of mechanics were not yet certain, Bernoullis and D’Alembert faced the discharge problem using their own principles and approaches to reach essentially the same end. D. Bernoulli adopted the principle of conservation of the living forces, and the equality between the potential ascent and actual descent. J. Bernoulli, although recognizing that the principle of living forces was true, but still not accepted by all philosophers, adopted Newton’s concept of a motive force impressed on a body, which, in modern terms, equated to the variation of its kinetic energy. He then introduced a translation technique to develop his formulation of the discharge problem, which consisted in translating the effects of motive forces from intermediate layers to the uppermost surface of the water contained in a vessel. D’Alembert, on its turn, because of his rejection to the concept of force, worked not on the problem of discharge in terms of the impressed force, but rather on its effect, in terms of the travelled space and velocity.
It was shown that the formulations thus obtained by these authors, apart from differences in nomenclature and symbology, essentially led to the same results, and that they were applied to solve the same steady and non- steady flow problems. It was possible to conclude that after D. Bernoulli’s great success with Hydrodynamics in 1738, the two other authors felt that they were at least as capable if not superior to D. Bernoulli in accomplishing the proposed tasks, but that was too late for J. Bernoulli and D’Alembert, because Hydrodynamics was soon considered a landmark. These developments occurred at about the same time, in a kind of competition for priority in which Euler seemed to have tacitly accepted the role of presiding over the disputes, in a time when these ferocious discussions on priority were rather common.
However, it was Euler who brought the fluid mechanics problem of discharge to a new and definitive level with two publications at about the same time: one about a one-cylinder pump to deliver water through a piping system to an elevated reservoir, and another considering the forces that arose on the walls of the conduit due to friction. For the first time, the pressure force and the friction force appeared explicitly in the formulations of fluid flow through conduits. In these publications, the pressure in its modern sense has made its appearance. And by using Newton’s second law, he equated the flow convective acceleration in a conduit of any shape to the applied forces, namely, gravity, pressure and friction. However, the friction force was built under the wrong assumption that, as for the case of solid friction, the fluid friction force was proportional to the pressure. As turned out to be much later realized, Euler indeed did not recognized that the friction force was essentially a viscous effect, and hence independent of the applied pressure.
Finally, Lagrange’s memoir on the theory of fluid motion of 1781 is presented as a sequel to these first theoretical constructions. Despite the fact that Lagrange did not approach the subject with the eyes of practical applications, he had contributed to the subject with new mathematical resources, like the introduction of the velocity potential, and the application of power series expansion in fluid mechanics.
References
- Bernoulli, D. (1968a). Hydrodynamics. Jointly Translated with Bernoulli, J. Hydraulics from the Latin by T. Carmody and H. Kobus. Dover Pub. Co.
- Bernoulli, J. (1714). Meditatio de natura centri oscillationis. Opera omnia. https://books.google.com.br/books?id=10EiPJr29RUC&pg=PA168-IA2&lpg=PA168-IA2&dq=Bernoulli,+J.+%281714%29+Meditatio+de+natura+centri+oscillationis,+Opera+omnia&source=bl&ots=jwoGTH4vUT&sig=Gbvscu9wvgfgZCTymkuTx2KJGGw&hl=pt-BR&sa=X&ei=iKAIVdaNC5OXyATEu4HwAw&ved=0CCMQ6AEwAQ#v=onepage&q=Bernoulli%2C%20J.%20%281714%29%20Meditatio%20de%20natura%20centri%20oscillationis%2C%20Opera%20omnia&f=false
- Bernoulli, J. (1968b). Hydraulics. Jointly Translated with Bernoulli, D. Hydrodynamics from the Latin by T. Carmody and H. Kobus. Dover Pub. Co.
- Blay, M. (2007). La sience du mouvement des eaux―De Torricelli à Lagrange. Paris: Éditions Belin.
- Calero, J. S. (2008). The Genesis of Fluid Mechanics 1640-1780. Series: Studies in History and Philosophy of Science (Vol. 22). Berlin: Springer.
- D’Alembert, J. R. (1743). Traité de Dynamique. https://ia902607.us.archive.org/16/items/traitdedynamiqu00dalgoog/traitdedynamiqu00dalgoog.pdf
- D’Alembert, J. R. (1744). Traité de l’ équilibre et du mouvement des fluides: pour servir de suite au traité de Dynamique. http://echo.mpiwg-berlin.mpg.de/ECHOdocuView?mode=imagepath&url=/permanent/library/XHFB58ED/pageimg
- D’Alembert, J. R. (1752). Essai d’une nouvelle théorie de la résistance des fluides. http://books.google.com.br/books?id=Goc_AAAAcAAJ&printsec=frontcover&hl=pt-BR&source=gbs_ge_summary_r&cad=0#v=onepage&q&f=false
- Darrigol, O. (2005). Worlds of Flow: A History of Hydrodynamics from the Bernoullis to Prandtl. Oxford: Oxford University Press.
- Eckert, M. (2002). Euler and the Fountains of Sanssouci. Archive for History of Exact Sciences, 56, 451-468. http://dx.doi.org/10.1007/s004070200054
- Euler, L. (1754). Sur Le mouvement de l’eau par dês tuyaux de conduite. [Eneström index] E 206. http://eulerarchive.maa.org/
- Euler, L. (1757). Principes generaux du mouvement des fluides. [Eneström index] E 226. http://eulerarchive.maa.org/
- Euler, L. (1761). Tentamen theoriae de frictione fluidorum. [Eneström index] E 260. http://eulerarchive.maa.org/
- Hankins, T. L. (1970). Jean d’Alembert Science and the Enlightenment. Oxford: Clarendon Press.
- Huygens, C. (1669). Regles du mouvement dans la rencontre des corps. Journal de Sçavans. http://gallica.bnf.fr/ark:/12148/bpt6k581246/f23.image.langPT
- Huygens, C. (1673). Horologium oscillatorium, sive de motu pendulorum ad horologia aptato demonstrationes geometricae. http://books.google.com.br/books?id=YgY8AAAAMAAJ&printsec=frontcover&dq=inauthor:%22Christiaan+Huygens%22&hl=pt-BR&sa=X&ei=-JjqU-_rC6K-sQTOuoGgDg&ved=0CCkQ6wEwAQ#v=onepage&q&f=false
- Huygens, C. (1929). De Motu Corporum Ex Percussione. In Ouvres, La Haye. http://visualiseur.bnf.fr/CadresFenetre?O=NUMM-77865&I=7&M=pagination
- Iltis, C. (1971). Leibniz and the Vis Viva Controversy. Isis, 62, 21-35. http://dx.doi.org/10.1086/350705
- Lagrange, J. L. (1869). Mémoire Sur la Théorie du Mouvement des Fluides. Ouvres, 4, 695-750. Paris: Gauthier-Villars.
- Mach, E. (1919). The Science of Mechanics. Chicago & London: The Open Court Publishing Co.
- Torricelli, E. (1644). Opera Geometrica. http://archive.org/stream/operageometrica00torrgoog#page/n212/mode/2up
- Truesdell, C. A. (1955). Rational Fluid Mechanics, 1687-1765. In C. A. Truesdell (Ed.), Opera Omnia (Series II, Vol. 12). Lausanne: Orell Füssli.
NOTES
1This nomenclature comes from the fact that one of the goals in problems of this type is the calculation of the flow velocity in conduits, which allows the determination of the volume of flow per unit of time―the flow-rate―, or the discharge.
2There are controversies about dates raised by J. Bernoulli, who claims having developed his theory as earlier as 1732. In fact, Hydraulics by J. Bernoulli was actually published in 1743, but it was pre-dated to 1732. For an account on the disputes between Daniel Bernoulli and Johann Bernoulli, see the preface by Hunter Rouse on Hydrodynamics (Bernoulli, 1968a) & Hydraulics (Bernoulli, 1968b) .
3According to the records in ‘The Euler Archive’ http://eulerarchive.maa.org/, a treatise with the title Tentamen theoriae de frictione solidorum (!) was read to the Berlin Academy on December 2, 1751, and it was presented to the St. Petersburg Academy on June 17, 1754.
4Sublimity (Lat. sublimitas, Ital. sublimità), is a parameter introduced by Galileo in the Dialogues, being the height from where a heavy body would have to fall (free falling or on an inclined plane) to reach at the end of its descent the said velocity. With this parameter, Galileo was able to complete geometrize the kinematics of free falling bodies.
5Torricelli states that his mentor Benedetto Castelli (1578-1643), knew that the quatities of water issuing from equal apertures are proportional to the square root of their respective heights. However, according to Poleni (Raccolta D’Autori Italiani Che Trattano Del Moto Dell’Acque (Edizione Quarta), Tomo VI, 1823. POLENI, Giovanni; Del Moto Misto Dell’Aqua), Torricelli had said that he was taught by Castelli that the quantities of water are in direct proportion to their heights, and therefore found appropriate to correct this in his book on the motion of waters.
9See http://www.codecogs.com/library/engineering/fluid_mechanics/pipes/surge/rigid-column-theory.php.
10For a Portuguese translation by the author access http://eulerarchive.maa.org/.
11Note that Euler is working in terms of absolute pressures in these developments.
12See Calero (2008: pp. 426-435) and Truesdell (1955: pp. IX-CXXV) . Euler’s work is also discussed in the perspective of eighteenth century fluid dynamics research by Darrigol and Frisch (2008). https://www-n.oca.eu/etc7/EE250/texts/darrigol-frisch.pdf






































