Advances in Historical Studies
Vol.04 No.01(2015), Article ID:55155,8 pages
10.4236/ahs.2015.41002
Archimedes’ Psammites and the Tradition of Italic Thought of Science
Giuseppe Boscarino
Cultural Association S. Notarrigo, The Italic School, Sortino, Italy
Email: gpp.bos@libero.it
Copyright © 2015 by author and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 21 January 2015; accepted 2 March 2015; published 30 March 2015
ABSTRACT
It is intended to confute the opinion of a Platonic Archimedes, through the study of the fundamental theses of his Sandreckoner (Psammites) and of its particular logical-linguistic aspects, but especially of an Aristotelic Archimedes, as Delsedine (1970) maintains in his article “L’infini numérique dans l’Arénaire d’Archimède”. He writes: The Sandreckonerrépond à la nécessitè d’a- dapter la notation numérique à l’idée de l’infinité potentielle de l’ensamble des nombres naturales”1. First, it is focused on the general aspects of the work, which highlight its Enlightenment and Pythagorean―Democritean character, then it is passed to the analysis of its particular linguistic and logical aspects and of its fundamental theses, translated into symbolic form, in which it is still giving prominence to its Pythagorean-Democritean or Italic character (Boscarino, 1999, 2010, 2011, 2012) .
Keywords:
Apeiron, Meghethos, Aritmos, Monas, Pletos, Pythagorean-Democritean or Italic Tradition of Though, Platonic-Aristotelian or Ionic Tradition of Though

1. Introduction beyond the Prejudices on a So-Called “Greek Science”
Archimedes’ Psammites is a work of mathematics, if you want arithmetic, but also astronomy, physics, an important and valuable source is historical information in the field of the history of science, especially of astronomy, of mathematics, of science and technology, but especially, in our opinion, a work of profound cultural significance, philosophy and epistemology, not highlighted by the different readings which have been given about it.
It denies inveterate stereotypes about the nature of the so-called Greek science and personality of Archimedes; for this reason, I made it the object of my greatest scientific and philosophic attention, in the reading as also in the commentary and interpretation, a complex work therefore, both from the scientific and philosophical point of view and from the linguistic one.
The work meanwhile denies the cliché of an aseptic Greek science, like the one that appears in the text of Euclid, made up of definitions, axioms and theorems, without cultural background, since Archimedes’ work is written in the form of a letter to a king, Gelon of Syracuse, who is credited with a certain mathematical competence and a certain astronomical knowledge2 and which is intended to engage him in a fight against a prejudice or more critical and fideistic prejudices, common in the religious beliefs of many, as of the poets and philosophers, namely that there cannot be any numbers which are capable of counting large multiplicities, as much as the grains of the sea sand can be, but also those ones forming the known universe.
We think of the poet Pindar, of the fifth century BC, lived for a time in Syracuse, which will be then Archimedes homeland, who had already written “the sand escapes the number” (Olympian Ode, II, 98) and all the contemporary or nearly so, to Archimedes, religious biblical literature, cheering the innumerability of the sand of the sea, the number of which can be known only by a wisdom superior to man’s one, which can be only God’s one (All wisdom comes from the Lord and it is with him for all centuries. The sand of the sea and the drops of rain and the days of the centuries, who can never count them? Only one is wise and very terrible sitting upon his throne: God)3.
Therefore deeply enlightened, ante litteram, work, so in the wake of the thought of Democritus, the only philosopher, who is mentioned in the surviving works of Archimedes, who dared to imagine a homogeneous universe, from the physical and metaphysical point of you, a world that consists of only physical atoms, as the grains of sand are, which Archimedes imagine forming his hypothetical physical universe, of which he wants to count the number, which is then neither inhomogeneous nor hierarchical, such as that of Plato and Aristotle, as in the wake of the thought of Parmenides, according to which “the not being neither you can think it nor you can express it, because thinking is the same as being”4, as well as in the wake of sophistic thought, of criticism of mythical and religious uncritical prejudice , not on a human scale.
Only those who are able to think in a mathematical way, that is as to say for Archimedes, in a rational way, this concludes is work, know how to become free of prejudice, or know how to think and nominate numbers as large as they want and assign them to multiplicities as well great as they want, they are too big as the entire universe that they know
I think finally, King Gelon, that all these things will seem unbelievable to most people, who are inexperienced in mathematical things, but those that will cultivate those ones and will apply to know the distances and sizes of the earth, the sun, the moon and the whole world, will admit the result of my demonstration. And that is why I have deemed it appropriate that even you took knowledge5.
The work denies then the other stereotype of a Greek mathematics, aimed at founding the science of geometry alone and take it forward, because it is directed to the foundation of a science of numbers, as is clear from the same testimony of Archimedes, in this work, in which it is said that Archimedes has already sent arithmetic, unfortunately lost, written to a scientist of his time, Zeuxippus.
But, I shall try to show to you, by means of geometrical proofs, which you will be able to follow, that, among the numbers named by me and exhibited in the writings sent to Zeuxippus, some exceed not only the number of the mass of sand equal in volume to the earth filled in the manner described by me, but also that of a mass equal in volume to the cosmos6.
We should ask ourselves why his writings of arithmetic have been lost and not those of geometry. We believe that the reasons were not random and accidental, but much deeper, external to the progress of science.
The work denies yet another prejudice about the progress of the Greek science in an unique sense, with no conflict on the field, only of Platonic-Aristotelian approach, especially in the field of astronomy, when it bears the testimony of a heliocentric system, such as that of Aristarchus, III century BC, of an entirely different approach, the Pythagorean-Democriteanone, that is not only of a not geocentric universe, such as that of Pythagorean Philolaus, but also non-finite and acentric, like that of Democritus.
But the work denies especially the inveterate prejudice, die-hard of a Greek, purely theoretical, contemplative, idealistic science, disconnected from the physical operations of measurement such as from the use of technical tools of measurement.
In the work it is described in an analytical way the use of dioptra that Archimedes designed to measure the apparent diameter of the sun, then to calculate the universe’s one and so its volume; it is recognized the use of hands and instruments in the field of scientific discovery.
I suppose that the diameter of the sun is larger than the side of the chiliagon inscribed in the maximum circle of the world. I suppose that, as Aristarchus found that the sun appears to us about like the seven hundred twentieth part of the circle of the zodiac; I myself, having examined it, in the same way, I have tried with tools to find the angle that subtends the sun and has its apex in the eye.
However it is not easy to measure this angle with precision, since neither the view nor the hands nor the tools, that are necessary to measure it, are pretty sure to let us know precisely it. For the moment it is not appropriate to extend our discussion on these things, especially because this kind of thing has been explained many times7.
Therefore a complex and multifaceted work, extremely interesting from the philosophical and epistemological point of view, as well as from the scientific and historical point of view, as well in the guise of a refined game, as that to want to count the number of grains of sand of the sea and the entire universe, formed by them, as by many atoms of Democritus.
We argued about a complex work not only from the point of view of the content, but also of the linguistic one, such that it becomes a witness in denying another prejudice, in our opinion, of a all Greek, rather Attic, indeed Athenian science (a Greece from a cultural and political state point of view never existed).
2. General Aspects of the Work
The work was written in Doric language, or rather in Syracusan dialect. The work then testified that there was a native science, with many poles, one of which was Syracuse, with its own cultural Pythagorean-Democritean tradition, which has its own language, the Doric-Syracusan one.
Let’s remember Hicetas and Ecphantus of Syracuse and the Pythagoreans, who, already in the fifth and fourth centuries BC, according the testimonies, speak of the earth’s rotation around itself, as a physical reality made up of indivisible atoms, then monads in the anti-Platonic and Aristotelian sense―Ecphantus of Syracuse said that “the principles of all things are the indivisible bodies and the vacuum: he first said that the monads of the Pythagoreans are corporeal”8.
A scholar on the luck of Archimedes in the rhetors and in the ancient Christian authors has written:
The language, in which the works of Archimedes (Heath, 1912) were written, has lost all traces of its original forms. If the Ionic dialect suited to the medicine, the attic to the philosophy and history, the Doric of Sicily, instead, to the science of Archimedes. The Heiberg with a methodical observation on the Archimedean writings, worthy of relief, trying to go back to its original forms, was able to deduce that only the Arenarius has had approaches to it, while all others have suffered additions and mutations by an interpolator who knew the Doric language9.
This, therefore, may lead us to speak of a not Greek and a-centric science, but of the center-eastern Mediterranean sea, with traditions of thought in conflict, first of all, between the Pythagorean and Democritean tradition of thought, to which we believe that Hicetas and Ecphantus of Syracuse ideally belong, and the Platonic-Aris- totelian one, and against whom he fought in his work, specifically in his work, the Sandreckoner, our Archimedes.
Archimedes, although he does not mention him, is on the wake of the Pythagorean Archytas of Taranto, V-IV, sec. BC, who, according to the testimony of Horace, has dared to count the number of grains of sand on the sea. Horace: The sand of the sea and the earth encloses you, Archytas, which counted it (te mensorem)10.
Mondolfo (1967) already in a very interesting note of his book. The infinite in the thought of classical antiquity, noted an ideal continuity between Archimedes and his predecessors Archytas and the Pythagoreans: According to the chronological order, from Archytas and Plato we should go to Aristotle; whom here instead we place after, to follow in Aristarchus and Archimedes the development of the computers problems of Archytas and other Pythagoreans11.
Archytas can be placed among those mentioned by Archimedes in his work: Some then (Archytas? our addition), although considering limited it (in number, the sand formed by grains, our addition), still think that no number can be nominated to be so great as to overcome its multiplicity12.
Archimedes then says: Names were given to a myriad and beyond a myriad the names that were given are fairly well known; they did nothing but repeat a myriad up to ten thousand myriads. However the numbers now indicated and ranging up to a myriad of myriads are called prime numbers (protoi), while a myriad of myriads of prime numbers is called the unity of the second numbers. We count by this unity for tens, hundreds, thousands and myriads of these unities up to a myriad of myriads. A myriad of myriads of second numbers is called unity of the third numbers. We count by these units for tens, hundreds, thousands and myriads of these unities up to a myriad of myriads...13 and so on, up to what we say soon after.
So Archimedes not only daresto count the grains of sand of the sea, as well as those that formed the entire universe, but as a good Pythagorean dares to build the numbers, with which we can count any multiplicity, which we can imagine.
In fact if the reality, the rational one, which is the real one, is Pythagorean-Democritan, made of atoms, or otherwise of elements, of grains of sand, which in the case of Archimedes become almost a kind of sensible representation of those ones, then it must be in principle countable, while the sensible reality is infinite, uncountable, chaotic, apparent, not true.
Both Democritus and the Pythagorean tradition have already represented really to themselves the atoms or the elements of reality as grains of dust in motion, as it is clear from this testimony, reported by Luria in his Democritus: Democritus considered the elements as resembling to grains of dust which move with great speed in the air, while some of the Pythagoreans considered as elements those same grains of dust (Luria, 2007) .
Therefore, it is possible to build, and then to count, starting from the element, the monad (the monas), or unity, the one as idea of one, ıone, not the number, but the quantity, the magnitude, multiplicities more and more which can be grouped in unities, higher monads, or otherwise said: from the unity of the series of prime numbers of the first period, to the unity of the series of second numbers of the prime period, 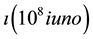 , to the unity of
, to the unity of
the series of the third numbers of the first period,  up to
up to 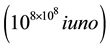 and from here
and from here
from the number indicating a multiplicity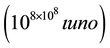 , taken as a new unit of greater period, or unity of the
, taken as a new unit of greater period, or unity of the
series of prime numbers of the second period, 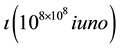 , which by now I place equal to A, to the unity of
, which by now I place equal to A, to the unity of
the series of second numbers of the second period,  , to the unity of the series of third numbers of the second period,
, to the unity of the series of third numbers of the second period,  , up to the multiplicity A of the second period,
, up to the multiplicity A of the second period,  and
and
over again from the unity of series of prime numbers of the third period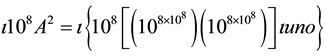 ,
,
or up to the multiplicity A of period, 108, or, 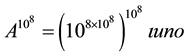 , a number made by the unit followed by 80 million of thousand millions of ciphers, called by Archimedes, a myriad of myriad of number a myriad of times a myriad of period a myriad of times a myriad (of unities), which we can now write in ciphers
, a number made by the unit followed by 80 million of thousand millions of ciphers, called by Archimedes, a myriad of myriad of number a myriad of times a myriad of period a myriad of times a myriad (of unities), which we can now write in ciphers
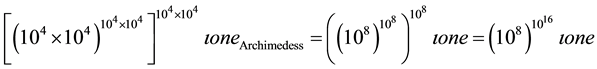
Note that in all the Archimedean speech the unity is not considered a number, such as Eecke (1921) or Loria (1914) in their comment on the work of Archimedes have so ambiguous represent it14 but, as the unity of measurement of the number, the idea of one, of an entity whether it is an one or a multiplicity, since, as already for the Pythagoreans and Euclid, the number is composed of the plurality made by of unities and the unity is the idea of one. Euclid says: “The unity is the entity that is said one”15.
In that 108 ıuno, 106 ıone, ..., these indicate multiplicities, are elements of the numbers, but as they indicate unities ,
, 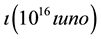 , ..., they are not a number, because they mean the multiplicity taken as such, as one, idea of one, unity, monad. From these unities the numbers are built as indicating multiplicities, counting multiplicities, 108 ıuno, 106 ıone, …
, ..., they are not a number, because they mean the multiplicity taken as such, as one, idea of one, unity, monad. From these unities the numbers are built as indicating multiplicities, counting multiplicities, 108 ıuno, 106 ıone, …
Archimedes does not place the unity in the series of numbers that he builds and that he names, as the Pythagoreans and Euclid had done, as is clear from the definition of the number of Euclid and the Pythagoreans by the testimony of Aristotle, where he writes: The one is not other than the measurement of a multiplicity and the number is not but a measured plurality and a plurality of measurements, therefore it is also logical that the one is not a number, since the unity of measure is not identified with the measurements, but both the unity and the one are a principle16.
Then in an illuminating testimony of Aristotle, we can read as he had already seen between the atomism of Democritus and the concept of number, as composed of unities, monads, which is that of the Pythagoreans and Euclid as of our Archimedes, an ideal continuity, a fundamental isomorphism.
“Democritus says it is impossible that a thing is generated by two things and that two things are generated by a thing, because he identifies the substances with indivisible magnitudes. Therefore it is obvious that it’ll be the same way for the number, if it is true that the number, as some say, is a composition of monads”17.
The reference to a presumed Platonism of Archimedes (Frajese, 1974) in this regard is a stretch and is out of place, because, in none of his writings, Archimedes mentions Plato, but Euclid and Democritus, for which the principles are ideas = elements (see the following testimony: Democritus calls the elements ideas, Democritus says that the principles of things are ideas)18. and the unity, the monad, can only be the beginning of the number, according to the testimony even of Aristotle:
“The one is the beginning of the number as number”19.
Therefore Pythagoras, Parmenides, Democritus, Euclid, Archimedes in the ideal line of Archimedes, not of Plato and Aristotle. But now we pass to analyze better in the following section the thesis of Archimedes in the Sandreckoner with those which he intends to refute.
3. Logical-Lexical Aspects Archimedes’ Psammites and Fundamental Thesis. Archimedes, a Pithagorean-Democritean
To enter more deeply into the Archimedean speech, first we translate some terms of his thesis into common language and into symbols, using in part Peano’s ideography ( Peano, 1960 , particularly we use his iota, ı, a linguistic logical operator that lets us shift from the individual or from the class to their idea, to the singleton, today we would name it in the extensional sense) and partly the symbols, as used in mathematical logic today.
1) Apeiron = not-finite, not-limited. I translate it in this way, because for us the term “apeiron” takes more the meaning, in the Archimedean context, as it is clear from the translation into symbols of his fundamental thesis, of negation of the finite, rather than of affirmation of the not-finite or infinite. In short, it asserts more the impossibility of a limitation of something rather than its non-limitation or infinity.
2) meghethos = volume, magnitudo
3) aritmos = the itself number, the mere number, the single number, the iota number = ın(iuno)
4) monas = ideas of one or ıuno, the one as one, the same one, auto tò én
5.1) pletos = multiplicity, plurality, M
but also
5.2) pletos = the number N, or N0 of a multiplicity.
In the second case 5.2 it assumes the meaning from one side of
5.2.1) operator N that lets shift from the multiplicity to its numerical value
N(M) = n(ıuno)
from the other side of
5.2.2) operator, N0, which lets shift from the multiplicity to its value of number as number
N0(M) = ın(ıuno)
For Archimedes meanwhile the class of numbers exists, such that
If 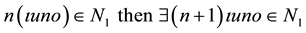 (Class of numbers that grows beyond any given number, n(ıuno).
(Class of numbers that grows beyond any given number, n(ıuno).
Now we enunciate what are the thesis that he intends to confute and then the thesis that he intends to prove.
3.1. The Thesis That Archimedes Intends to Refute
Let us now try to translate first, into words, the individual propositions that Archimedes intends to refute, and then in symbols, trying to enucleate of them the concept, by expressions, and then in the same way his fundamental thesis.
Some think that
Thesis. a) tou psammou ton aritmon apeiron eimein to pletei = the number of the sand is not-finite with respect to multiplicity20, and in symbols
If 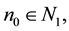 M = grains of sand, then
M = grains of sand, then  which we so read:
which we so read:
“Be n0 an element of a class of numbers whose elements grow over each given number, then there is not an operator that lets us shift, in our case by a given multiplicity of grains of sand, to a number, as such, and such that it is at the same time smaller than a certain number of the class of numbers that grow over any given number, or that it is limited by any of them”.
Others think:
Thesis. b)
Even considering the finite number of sand, they think that there cannot be a number that exceeds the number that indicates its multiplicity21.
And in symbols
that we can read
“For each multiplicity as large as you want, it is possible to assign a number, which limits it, but there is not a successor such that it is not equal to a number which corresponds to a multiplicity, that is there are no mere numbers as large as you want without corresponding a multiplicity to them”.
3.2. Thesis That Archimedes Intends to Prove
“But I will try to show by means of geometrical proofs that among the numbers appointed by me and exhibited in the writings sent to Zeuxippus, some exceed not only the number of sand equal in volume (meghetos) to the filled earth but also that of a mass equal in volume to the cosmos”22.
Now let us write that in symbols
that we can read, as follows
“For Archimedes mere numbers N1 are conceivable and therefore exist, against Thesis b), as big as you want, without corresponding a physical multiplicity to them, because it is possible to build, with elementary physical ope- rations of reproducible and controllable, then rational calculation―we would say today with a pen and paper.
But for Archimedes it is also possible to construct the operator, which corresponds once again to elementary physical operations of measurement, the use of dioptra, such that lets us assign the number to a multiplicity as large as you want, up to be equal to the multiplicity more as great as that which includes the universe as a whole, the pan, and not only the cosmos, and the number of which, against Thesis a), is limited by a mere number”.
Let’s see how in practice this proved model translates itself in Archimedes’ Psammites. N1 are the numbers of Archimedes; these are built, and then made possible, existing as multiple of unities (Monas), always higher than the unity of base, as we have seen in the previous section. Archimedes groups them into octads, in groups of eight. An octad has the following form, in modern notation, without unities, which, however, for Archimedes, as for Euclid, constitute an integral part of the number:

All this, in explicit form, can be written:
・ 1st Octad 1, 101, 102, 103, 104, 105, 106, 107 first numbers
・ 2nd Octad 108, 109, 1010, 1011, 1012, 1013, 1014, 1015 second numbers
・ 3rd Octad 1016, 1017, 1018, 1019, 1020, 1021, 1022, 1023 third numbers
・ 4th Octad 1024, 1025, 1026, 1027, 1028, 1029, 1030, 1031 fourth numbers
・ 5th Octad 1032, 1033, 1034, 1035, 1036, 1037, 1038, 1039 fifth numbers
・ 6th Octad 1040, 1041, 1042, 1043, 1044, 1045, 1046, 1047 sixth numbers
・ 7th Octad 1048, 1049, 1050, 1051, 1052, 1053, 1054, 1055 seventh numbers
・ 8th Octad 1056, 1057, 1058, 1059, 1060, 1061, 1062, 1063 eight numbers
・ Monas or unity of the first numbers ıuno
・ second numbers ı(108 ıuno)
・ third numbers ı(1016 ıuno)
・ fourth numbers ı(1024 ıuno)
・ fifth numbers ı(1032 ıuno)
・ sixth numbers ı(1040 ıuno)
・ seventh numbers ı(1048 ıuno)
・ eight numbers ı(1056 ıuno)
They allow you to assign to each imagined given multiplicity of grains of sand, with a single grain, thought of as a unity, element, atom-idea, monas, forming volumes of sand of spherical form, until that of the universe, the pan, whose center is the sun and the suburbs are the fixed stars, a mere number, which limits of it the numerical value, assigned to it by physical operations of measurement.
If for example to a sphere of diameter of 100 myriads of stadia formed by grains of sand, we assign a number of Archimedes, then there exists a mere number of Archimedes, which limits it.
In symbols:
Because N(Sf10.000stadia) < 10 × 1032 = 1033, we have then that
N(Sf10.000stadia) < 10 × 1032 = 1033, number of Archimedes
N(Sf100×10.000stadia) < 100 × 104 × 1033 = 1039
This scheme can be repeated until the larger sphere, of given diameter, which is that of the universe, whose number of grains would be lower anyway of one of the numbers of Archimedes. In symbols:
N(Sfsand) = N(Sffixed stars) < 1000 × 104 × 1056 = 1063 = number of Archimedes.
4. Archimedes: A Platonic-Aristotelian or a Pythagorean-Parmenidean-Democritean?
In the light of this thesis of affirmation of the existence of mere numbers, which does not correspond to any physical multiplicity, is it possible to think of an Archimedes of Platonic formation or, as Delsedime says, of Aristotelian mentality? (Dijksterhuis, 1956; Frajese, 1974; Gardies, 1980; Plutarch, 2001; Virieux, 1979) .
We think: Absolutely not!
For two very specific reasons.
First: Meanwhile, for Archimedes the numbers do not exist as such, in the Platonic sense, in a world apart, the supercelestial―at least there is no statement in his writing in this sense―but exist as logical entities, whose existence is guaranteed by the possibility to build them with elementary physical operations, such as the use of dioptra, that allows by measurements to assign a number to a spherical volume formed by a multiplicity of grains of sand, as large as the entire universe, the pan, but above all by the possibility of being able to build them, we would say today with pen and paper, by operations of reproducible and controllable, therefore rational calculation.
Second: Archimedes does not assert the existence of a potential numeric infinite, in Aristotelian sense, and the not-existence of infinite sets of numbers and of infinite physical magnitudes, but, as it is clear from our rigorous reconstruction of the thesis that Archimedes intends to refute and of what he intends to prove, that a multiplicities big as you want, be it the pan, which we can measure and know, there were other larger multiplicities, to which it is deemed not to be able to assign a number or measure them then, it is always indeed possible to assign a number (and this is Pythagorism, since everything is number), but also to restrict them with a larger number, although it does not correspond to any multiplicity (and this is even Pythagorism more that Platonism or Aristotelianism).
This is because the numbers that we build with the rational calculation are truer than the multiplicities that we gradually can measure or count; the real logos may precede the physis, indeed must precede it, because it is the necessary condition, though not sufficient of its being. Only if you can count the multiplicities as large as you want, you could verify the not only logical but also physical existence.
One thing that cannot be counted as logical necessity, it may not even exist physically. Philolaus, a Pythagorean said (V century BC): All the things that you know have a number: without the number would not be possible the think or the know anything23.
Then, Archimedes does not want to prove that a possible physical universe is finished, from the numerical point of view, but that it is possible that it is not-finite, since the existence of numerical unfinished sets guarantees of it the logic, although not physical, existence.
Archimedes does not oppose, as R. Mondolfo, writes, his idealistic infinite to real infinite of Aristarchus, reserved for the only domain of thought and of mathematical calculation24, because he is in Pythagorean agreement with the Aristarchus, as on the other hand the same Mandolfo notes.
Archimedes’ not-finite is Archytas’ one, Democritus and Lucretius, which claim not that the universe is not infinite but that a limit cannot put to it without contradicting ourselves , because of a thing of which it is said that has limit, you have to admit that there is always something that limits it.
Archytas said: If I could find at the end of the space, for example in the heaven of the fixed stars, could I extend a hand or a stick out of that? or do not I? To say that you cannot, it is absurd25.
And yet the Democritean Lucretius: It seems clear that of none thing there might be extreme, if there is not something else that limits it26.
Archimedes, of this universe, instead gives of it the logical and not only rational possibility in Pythagorean sense, as Archytas, Democritus and Lucretius, with his prove, by elementary physical operations of measurement and of rational calculation, which are not in the Aristotelian speech about the assertion of the existence of the potential infinite, of numbers ever larger of any number that can be assigned to a multiplicity that fills a volume as large as you want.
The pan here is only then a metaphor, a rhetoric figure to indicate a philosophical point of view in agreement to the tradition of Pythagorean-Parmenidean-Democritus thought, for that the reason is the necessary condition of the physical being, whose existence is proved from elementary physical operations, which are the sufficient condition of his physical being. “The Pythagoreans say that (guide) is the reason: not the reason in any of its forms, but the one that lays the foundations in the mathematics”27.
In short, it is illuminating in this regard the following, even if distorted, testimony, of Aristotle on the Pythagoreans, from which a philosophical-epistemological conception emerges in agreement with what which will be of Parmenides and Democritus, and why not, of Archimedes: “They (the Pythagoreans) seek the reason and the cause not relating to what is observable, but rather forcing the phenomena brought back to some of their reasons and opinions, and trying in this way to harmonize them and lead them to an ordered whole”28.
From this, brutally empiricist, his point of view, all the numerical construction of Archimedes, would appear to Aristotle a mad and fantastic construction of a visionary, not the fulfillment of his potential infinite!
Besides, the fact that Archimedes was familiar with the actual infinite, as it is said from that emerges today from his lost and found again writings, would denote for an anti-Aristotelian and once again Democritean Archimedes, since the concept of infinity was congenial to this philosopher, the only philosopher mentioned by Archimedes.
Acknowledgements
The author is very grateful to Prof. Armando Anzaldo for his assistance and advice about the English translation.
References
- Aristotle (1973). De caelo. Bari: Laterza.
- Aristotle (1971). Metaphysics. Bari: Laterza.
- Boscarino, G. (1999). Tradizioni di pensiero. La tradizione filosofica italica della scienza e della realtà (p. 412). Sortino (SR): La scuola italica. (To be Consulted by Anyone Who Wants a Wider and More Complex Treatment over the Centuries VI, V, IV BC of the Greek World, the Two Traditions of Thought in Conflict, the Pythagorean-Parmenidean-Demo- critean Tradition and the Platonic-Aristotelian Tradition.)
- Boscarino, G. (2010). The Mystery of Archimedes. Archimedes, Physicist and Mathematician, Anti-Platonic and Anti-Aris- totelian Philosopher. In The Genius of Archimedes―23 Centuries of Influence on Mathematics, Science and Engineering. History of Mechanism and Machine Science (Vol. 11, pp. 313-322). Springer.
- Boscarino, G. (2011). The Onto-Epistemological Background of Archimedes’ Mathema. Selected Proceedings of the SILFS 2010 International Congress. Logic and Philosophy of Science, 9, 111-129.
- Boscarino, G. (2012). At the Origins of the Concepts of Máthema and Mekhané: Aristotle’s Mekhanikà and Archimedes’ Tropos Mekhanikòs. In T. Koetsier, & M. Ceccarelli (Eds.), Explorations in the History of Machines and Mechanisms Proceedings of HMM 2012 (Vol. 15, pp.449-461). Springer.
- Delsedine, P. (1970). L’infininumériquedansl’ Arénaired’ Archimède. Archive for History of Exact Sciences, I, 345-359. http://dx.doi.org/10.1007/BF00329816
- Delsedine, P. (1970). Uno strumento astronomico descritto nel corpus archimedeo: La dioptre di Archimede. Physis-Rev. Internaz.Storia Sci., 2, 173-196.
- Diels-Kranz, DK (2004). Presocratici. Bari: Laterza.
- Dijksterhuis, E. J. (1956). Archimedes. Copenhagen.
- Eecke, P. V. (1921). Les oevres completes d’Archimède. Paris: Bachelier.
- Frajese, A. (1974). Opere di Archimede. Torino: Utet.
- Gardies, J. L. (1980). La méthodeméecanique et le platonisme d’Archimède. Revue Philosophique de la France e de l’Etranger, Tome CLXX, 39-43.
- Heath, S. T. (1912). The Works of Archimedes. New York: Dover Publications, Inc.
- Loria, G. (1914). Le scienze esatte nell’antica Grecia. Torino: Hoepli.
- Luria, S. (2007). Democrito. Milano: Bombiani.
- Mondolfo, R. (1967). L’infinito nel pensiero dell’antichità classica. Firenze: La Nuova Italia.
- Peano, G. (1960). Formulario Mathematico. Roma: Cremonese.
- Plutarch’s Lives (2001). Marcellus. New York: The Modern Library.
- Virieux, R. A. (1979). Le platonismed’ Archimède. Revue Philosophique de la France e de l’Etranger, Tome CLXIX, 189- 192.
NOTES
1See Delsedine, 1970 .
2See Sandreckoner I, 3.4. For citations see the book by Boscarino (2012) , Un mondo di sabbia. L’Arenario di Archimede e la tradizione di pensiero italica della scienza. Altromondo publisher, Padova, 2012, to which references are made and where it is translated Archimedes’ Psammites with the Italian translation of it of Boscarino (2012) .
3See Bible, Ecclesiasticus, 1.1, 1.6.
4See Diels-Kranz (2004), 28, B 2.5, B, 3 .
5See Sandreckoner IV, 20.
6See Sandreckoner I, 3.
7See Sandreckoner I, 10, 11.
8See Diels-Kranz (2004), 51.2 .
9See Antonio Quaquarelli, The luck of Archimedes in rhetors and in ancient Christian authors, in Archimedean celebrations of the twentieth century, vol. IV, Syracuse, 1965.
10See Horace, Carmina, I, 28.
11See A. Quaquarelli p. 219.
12See Sandreckoner 1.1.
13See Sandreckoner III, 2.
14See p. 365 Eecke e Loria p. 755.
15See Euclid, Book VII, def. 1 and def. 2.
16See Aristotle (1971) Metaphysics, XIV, 1088th, 5 .
17ibidem, Metaphysics VII, 1039a, 10.
18See DK (2004) , 68 B, 57.
19See Aristotle (1971) Metaphysics, I, 1052b, 20 .
20See Sandreckoner 1.1.
21Ibidem 1.1.
22Ibidem 1.3.
23See DK (2004) 44, B. 4.
24See cit. w. p. 220.
25See DK (2004) 44, A, 24.
26See Lucretius, De rerum natura, Book I, lines 961-962.
27See DK (2004) 44, A, 29.
28See Aristotle (1973) De caelo, 2.13 .










