International Journal of Geosciences
Vol.09 No.12(2018), Article ID:89537,8 pages
10.4236/ijg.2018.912041
A New Method to Determine the Grid Directions in Reservoir Numerical Simulation
Ming Li1, Luyi Tong1, Xiaodong Peng1, Guiping Nie2, Yan Lu1*
1Zhanjiang Branch of CNOOC Limited, Zhanjiang, China
2Engineering Technology Company of CNOOC Energy Technology & Services Limited, Zhanjiang, China

Copyright © 2018 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY 4.0).
http://creativecommons.org/licenses/by/4.0/



Received: November 19, 2018; Accepted: December 25, 2018; Published: December 28, 2018
ABSTRACT
Grid direction selection and grid size design are two important elements that need to be considered in the grid direction design in reservoir numerical simulation. Reservoir engineers normally utilize geological data (such as the distribution of fractures, low permeability zones, faults and major stress) and simulation experiences to design the grid direction of simulation model qualitatively. The research of the paper indicates that the key to determine the grid direction is to determine the principal permeability direction. Under the circumstances of few static materials, a new grid direction determination method has been developed by using field data (well location map and inter-well permeability) on the bases of Darcy’s law and tensor analysis theory. The grid direction of WZ11-7 Oilfield simulation model has been determined using four production wells and two production zones (L1 and L3) in WZ11-7-2 well group, the results are in conformity with the geological studied major stress. Therefore, this method can give insights into the numerical simulation study.
Keywords:
Reservoir Numerical Simulation, Grid Direction, Black Oil Model, Permeability Anisotropy, Tensor Analysis

1. Introduction
Grid direction selection and grid size design are quite important, and should be considered in reservoir numerical simulation. Common grid direction selection should follow the following principles [1] : 1) grid direction should be consistent with the regional boundary (oil and gas, oil-water boundary lines, fault lines, reservoir pinch lines, well networks, or structural symmetry lines) and well pattern direction as far as possible; 2) grid direction should take into account reservoir nature, namely, the coordinate system should be parallel (or perpendicular) to the main axis of permeability, or approximately in line with the direction of the sedimentary channel (or perpendicular to the direction of the river), at the same time, the number of non-effective grids should be minimized; 3) grid direction should conform with existing (proposed) wells, which means that most of the wells should be located in the middle of the grid and that there is at most one well in a grid, furthermore, there must be at least one empty grid between two wells. However, if the direction of main axis of the permeability is not known, or there is not exact knowledge about the sedimentary channels, the principles listed above cannot work, and the simulation personnel have to design the simulation model at will. To enhance the accuracy of simulation results, a new grid direction determination method was developed.
2. Theoretical Basis for Simulation Grid Direction Design
When building a simulation model, it is necessary to split the actual reservoir into grid blocks. The center point of each grid is called a node, and the physical parameter value at each node represents the average of the physical parameters within the block [2] . For large-scale reservoir simulation models, coarse grids are generally used. However, as a coarse grid may contain various layers, joints, developed fractures, and rocks of different sedimentary facies types, the permeability values (KX, KY, KZ) in each direction (X, Y, Z) of the grid node may not be the same, thus, anisotropic phenomena appears. For example, the permeability along the bedding plane, the fracture development direction, and the river channel is high, while the permeability in these vertical directions is low [3] . Especially for reservoirs with low permeability and strong heterogeneity, the phenomenon of permeability anisotropy is ubiquitous.
Studies have shown that the permeability can be expressed as a second-order symmetric tensor [4] . For three-dimensional space, the permeability tensor [K] can be expressed as Equation (1).
(1)
where Kij = Kji, [K] is a symmetric matrix with 6 independent variables.
For two-dimensional space, Equation (1) can be deformed to Equation (2).
(2)
According to the tensor analysis theory [4] , Equation (1) has three mutually perpendicular main directions; Equation (2) has two mutually perpendicular main directions. If the main direction is used as coordinate axis, Equation (1) and Equation (2) can be expressed as Equation (3) and Equation (4).
(3)
(4)
Based on permeability tensor concept, Darcy’s law [5] can be expressed as
(5)
where
(6)
Φ is the potential in seepage flow field, which is a zero order tensor, and its gradient gradΦ is a first order tensor.
According to Equation (1), Equation (5) can be expressed as the following matrix equation:
(7)
when expanding the Equation (7)into three directions:
(8)
when coordinates coincide with tensor spindles.
(9)
Things above show that the choice of the coordinate system, that is, the condition of the grid direction design is to take the main direction of the permeability tensor as the main direction, otherwise, a certain degree of error will occur; and the nature of grid direction design is essentially to determine the main permeability direction. And the following can be further inferred:
1) For the anisotropic permeability, the values may not be equal in all directions, but they are not mutually independent. Through the analysis above, we can tell that for the three-dimensional situation, permeability values in six directions alone can determine three main directions, and permeability in all the other directions can be further obtained; for the two-dimensional case, permeability in two directions can calculate the permeability in all the other directions.
2) The permeability tensor takes the maximum or minimum value in the main axis direction, that is, the directions of maximum and minimum permeability are perpendicular to each other.
3) The actual three-dimensional geometry of the permeability tensor in reservoir underground is an ellipsoid. If the main axis direction is taken as the sphere axis, the geometric equation [1] is
(10)
In two-dimensional horizontal cross section of the ellipsoid sphere, the geometric equation is
(11)
Therefore, field data can be applied to obtain the main direction of permeability tensor, namely, grid direction.
3. Grid Direction Design
The essence of grid direction design in reservoir simulation is to obtain the main permeability direction, that is, to obtain the direction cosine of the main permeability [3] .
As to formula (5), since the direction of the pressure gradient generated by the fluid flow is not the same as the main direction of the permeability, there will be an angle θ between the percolation velocity vector and the , assuming this cosine as cosθ and the permeability in the flowing direction as Kv, thus,
(12)
which can be further obtained [3] :
(13)
Assuming that vector  in the main permeability directions are:
in the main permeability directions are: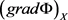 ,
,
, and based on formula (13) can get:
,
,
, and based on formula (13) can get:
(14)
Assuming that the cosine between velocity vector and 3main permeability directions are: cosα, cosβ, cosγ, then:
(15)
Substituting formula (15) into the formula (14):
(16)
Due to the influence of sedimentation and compaction, the vertical permeability of reservoirs is the smallest one among the main direction permeability tensor. In general simulation calculation, the vertical direction can be used as the Z direction of the grid. Therefore, only the two main directions (X-Y) on the two-dimensional plane need to be considered.
As illustrated in Figure 1, let the angle between the connection direction of well A and well B and the axis of KX be θ, let the angle between the connection direction of well A and well C and be α2, let the angle between the connection direction of well A and well D and be α3, let the permeability between well A and well B, well A and well C, well A and well D be K1, K2, K3 respectively. Then, from the geometric relationship of Figure 1
(17)
(18)
(19)
where m = KX/KY.
Assuming a2 = K1/K2, a3 = K1/K3, then formula (16)-formula (18) can get:
(20)
(21)
(22)
(23)
From formula (20), two angles θ1 and θ2 differing by π/2 radians can be obtained. Generally, the angle θ which makes m > 1 should be chosen as the angle between the and the KX axis, and the other angle should be the angle between and KY. When θ is positive, rotate θ degree from clockwise will be the direction of KX; When θ is negative, rotate θ degree from clockwise
Figure 1. Schematic diagram of inter-well permeability.
will be the direction of KY, in this way, the X-Y direction in simulation grid will be determined.
In the actual reservoir simulation, due to the heterogeneity of reservoirs, grid directions within a simulation layer could be different. Generally, representative well groups can be used as basic units to calculate the directions first, and the direction of the layer and the entire simulation reservoir is obtained by weighted average [3] . In addition, grid direction which is consistent with the boundary (fault) and the direction of the flow (water injection and production well) will reduce the truncation error.
I think the method can only handle a homogeneous reservoir system. How can the heterogeneity be introduced in this method? Please add a description where you deal with multiple realizations and heterogeneity in part 2 Grid direction design. What changes should be done in the mathematical formulation (if any) to account for reservoir uncertainty and heterogeneity?
4. Case Analysis
For case analysis, please add the reference of the data source, main initial well data, and the actual well map before a schematic plot in Figure 2.
Well location map of Block WZ11-7-2 in WZ11-7 Oilfield in Nanhai West is shown in Figure 2, the angle (α2) between the two lines (one line is from Well WZ11-7-2 to WZ11-7-1, the other is from Well WZ11-7-2 to Well WZ11-7-4) is 30˚, the angle (α3) between the two lines ( one line is from Well WZ11-7-2 to WZ11-7-1, the other is from Well WZ11-7-2 to Well WZ11-4N-1) is 125˚. The inter-well permeability is calculated from the average log interpretation permeability (Table 1 into formula (20), the calculation results are θ1 = −7.7˚, θ2 = 82.3˚).
Table 1. Inter-well permeability data in Block WZ11-7-2.
Figure 2. Inter-well permeability diagram in Block WZ11-7-2.
According to formula (21): when θ1 = −7.7˚, m = 0.95 < 1; when θ1 = 82.3˚, m = 1.2 > 1, then, θ should adopt 82.3˚. Rotating the line (WZ11-7-2 → WZ11-7-1) clockwise by 82.3˚ will obtain the X direction of L1 Formation; rotating the line anticlockwise by 7.7˚ will obtain the Y direction. If KX adopts the value derived from geological data, KY takes 0.8 times of KX.
2) Formation L3
Similarly, a2 = K1/K2 = 0.544, a3 = K1/K3 = 0.49, according to formula (19)
θ1= −7.5˚, θ2 = 82.5˚
According to formula (21): when θ1= −7.5˚, m = 0.924 < 1; when θ1 = 82.5˚, m = 1.43 > 1, then, θ should adopt 82.5˚. Rotating the line (WZ11-7-2 → WZ11-7-1) clockwise by 82.5˚ will obtain the X direction of L3 Formation; rotating the line anticlockwise by 7.5˚ will obtain the Y direction.
Based on the calculation results of the two main producing layers, rotating the line (WZ11-7-2 →WZ11-7-1) clockwise by 82.4˚ and rotating the line anticlockwise by 7.4˚ will obtain the X and Y direction of the whole simulation area. The results are in conform with the geological analysis (the maximum principal stress orientation is 79˚ North East).
An comparison between geological analysis and the results obtained from this method is needed for verification and validation, and some kind of numerical simulation is needed to support the conclusion “which enhance the accuracy of simulation results” in Conclusion part, line 3.
5. Conclusions
1) This paper puts forward a grid direction determination method which is based on field data in reservoir simulation. In this way, the grid directions can be determined only by well location map and inter-well permeability, which enhance the accuracy of simulation results.
2) The essence of grid direction determination is to obtain the main permeability direction, and the key parameter for calculating the value is inter-well permeability. Normally, the average permeability derived from well-to-well interference test or the log interpretation is used as the inter-well permeability.
3) While applying this method, it should be combined with geological data (such as crack direction, principal stress direction or boundary conditions), and the calculation results of this method cannot be used deliberatively.
Acknowledgements
This work is supported by the National Science and Technology Major Project of China (2016ZX05024-006).
Conflicts of Interest
The authors declare no conflicts of interest regarding the publication of this paper.
Cite this paper
Li, M., Tong, L.Y., Peng, X.D., Nie, G.P. and Lu, Y. (2018) A New Method to Determine the Grid Directions in Reservoir Numerical Simulation. International Journal of Geosciences, 9, 680-687. https://doi.org/10.4236/ijg.2018.912041
References
- 1. Yuan, Y.Q. and Yuan, Q.F. (1995) Application of Black Oil Model in Oilfield Development. Petroleum Industry Press, Beijing.
- 2. Liu, Z.R. and Xin, Q.L. (1993) Reservoir Description Principle and Method Technology. Petroleum Industry Press, Beijing.
- 3. Xu, W. and Gao, S.H. (1999) Grid Direction Determination in Numerical Simulation. Petroleum Exploration and Development, 26, 58-60.
- 4. Zhang, R.J. (2004) Tensor Analysis Tutorial. Tongji University Press, Shanghai.
- 5. Ge, J.L. (1982) Seepage Mechanics of Oil and Gas Reservoirs. Petroleum Industry Press, Beijing.
Nomenclature
K = Formation permeability, D
= Seepage velocity vector, m3/Ms
= Fluid viscosity, mPa・s
= Fluid potential, MPa
p = Fluid pressure, MPa
= Fluid density, g/cm3
h = Height, m




