Received 3 October 2015; accepted 15 December 2015; published 18 December 2015

ABSTRACT

At present, an investigation of the lunar ground at great depths is of paramount importance. This investigation can be carried out using decameter and meter waves. This article aims to analyze the variations of the reflection coefficient at decametric, meter and decimeteric bands. A possibility of determination of lunar ground characteristics by bistatic radar using powerful ground-based transmitters at VHF and UHF bands and a receiver aboard a Moon’s satellite is analysed. Appropriate algorithms are considered for determination of the regolith layer thickness, dielectric permittivity, loss tangent, and density of the regolith and bedrocks. Expected results of measurements have been presented for a two-layer model of lunar ground, consisting of an upper layer with the loose porous rocks (regolith), and the rocks situated more deeply. Revealed regularities are a basis for determining the distribution of the permittivity in subsurface layer.

Keywords:

Bistatic Radar, Lunar Ground, Regolith, Reflection Coefficient, Permittivity

1. Introduction

In 2007, the Russian program of the Moon and near-lunar space exploration started. The space research of the composition and physicochemical properties of the lunar regolith is a special branch of this program. The determination of the regolith density and thickness is of interest both of a practical and of a geological point of view. To understand the origin and evolution of the Moon, it is important to study the depth structure and composition of the soil. This information can be obtained by sounding the lunar ground using radar located on a spacecraft. Polar-orbiting satellite for an appropriate time provides the study of the Moon entire surface as both seen from the Earth, and the reverse side. Similar experiments are planned to carry out in the framework of the mission Luna-Glob using modulated radio signals in the frequency bands of 20 MHz and 200 MHz [1] .

The investigation of ground on the visible side of the Moon up to great depth is possible by method of bistatic sounding using powerful ground-based transmitters operating in the HF, VHF and UHF frequency bands, and a multichannel receiver aboard a lunar satellite.

The soil explorations are fulfilled now by NASA’s Mini-RF monostatic radar installed on the Lunar Reconnaissance Orbiter (LRO), which used also the Arecibo transmitter (emitting 200 kW at wavelength 13 cm) for bistatic studying of the lunar regolith [2] . Experiences of bistatic sounding the Moon realised by means of the first lunar missions, have shown, that frequency selection of signals accepted on the Earth allows us to separate the reference and reflected signals and to define the reflection coefficient and dielectric properties of surface rocks [3] [4] . The main regularities of the radio waves scattering by a rough lunar surface have been studied in papers [5] -[15] , where it is shown, that this method allows estimating density of the surface rocks and statistical characteristics of the relief irregularities. The layered structure of the ground was not considered for the interpretation of experiment results. In reviews [16] [17] there are presented the results of the first stage of developing the method for bistatic sounding of the heavenly bodies.

The idea of bistatic location of the Moon and planets using of high-power ground-based transmitters decameter and natural sources of radio emission has been proposed in [18] .

The study of the Moon ground at the great depth, which can be carried out at present by radar-tracking methods using decameter and meter waves, became relevant. The purpose of this article is the analysis of possibilities of sounding ground on the big depth by method of bistatic radar using powerful ground-based transmitters of meter and decameter radio waves and a receiver located on the lunar satellite. It is necessary to define the reflection coefficient for several wavelengths for the layered model of the ground depending on the position of the satellite and to solve a direct problem of bistatic sounding the lunar ground. For definition of ground characteristics, it is necessary to develop a method of solving an inverse problem, i.e. to find the horizontal and vertical distribution of the dielectric permittivity and density on a basis of the experimental values of the signal characteristics.

2. The Scheme of Measurements and Ground Model

Figure 1 shows the scheme of the bistatic location of the Moon in the observation plane. The Moon center is denoted as point B and the satellite is denoted as point A. The lunar satellite moves in a circular orbit shown by a dotted line. The satellite height is H, projection of the velocity vector on the observation plane is V. The unit vectors K and 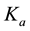indicate the direction of propagation of the incident wave on the surface and reflected one from the surface respectively. The satellite position is set by the angle 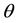and its distance from the Moon center

as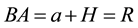, where a is the Moon radius. The position of point D on the surface is the center of reflected spot, where the incidence angle is equal to the angle of reflectiion. The distance from the satellite to this point D is equal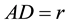. From the experiment geometry and a condition of equality of incident angle and reflected one the formula for the angles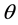, and the distance r was obtained:

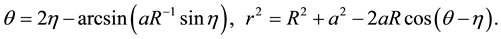(1)

It is suggested that the primary model of the lunar ground is the regolith layer lying on the bedrocks. The regolith density and the thickness of its layer depend on geologically activities of the certain region.

We will present the medium model as layered structure with complex dielectric permittivity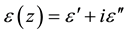, which depends on depth z. The lunar ground consists of the top layer of loose rocks of small density―regolith and underlying on denser bedrock. Figure 2 shows a small area of ground around the point D. On the top, the layer is situated regolith 1, and deeper―basic rock 2. The unit vectors of beam lines of incidence K and reflected wave K_a, angles of incidence 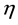on the regolith, on the bedrock 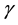and a projection of the velocity vector of satellite V are specified. We will result rough parameters of ground model. Possible values of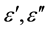, density of ground 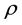and thickness l of a regolith layer are presented in [17] - [23] .

The real part of dielectric ground permittivity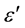, averaged for the central part of the visible side of the Moon, has been defined by ground-based radar. With these data for centimetric waves, in decimeter range. It is observed increase of dielectric permittivity while the wavelength increases: for, , and for,. This behavior of can be explained by increase of penetration depth of radio-waves into the subsurface; values of measured in centimeter and decimeter range corresponds to regolith, and joint influence of the regolith and bedrock, respectively. In the meter range this characteristic corresponds to influence of bedrock. Dielectric permittivity and density of rocks have been defined also by the laboratory measurements of the lunar ground samples delivered by missions “Apollo” [19] - [22] . Measurements of several samples have shown, that for loose samples, and for breccia.

The data about absorption coefficient of radio-waves by regolith are the most ambiguous, this characteristic is expressed by a known relation through a loss tangent. It is shown in the some publications, that for frequencies f = 10 − 1000 MHz depends on f weakly and for different samples of the lunar ground

has values from 10⁻³ up. Indirect data about possible values, and have been received from measurements of samples of the dehydrated terrestrial rocks―analogues of the lunar ground [17] - [21] . It turned out, that there is a simple connection between and density of rocks, corresponding to empirical formulas

or (2)

where has dimension g∙сm⁻³.

The thickness of the regolith layer l has been estimated according to seismic data from space vehicle impact against the lunar surface and registration of ground oscillations by registration of seismic sensors after falling spacecraft on the Moon surface. For dark sites of the surface―“lunar mare” it was found out l » 2 − 5 m, and for light areas―“continents” l » 8 − 15 m. It is supposed, that flat areas of the big craters can have a little thickness of regolith, and in some areas, the thickness of the regolith layer changes smoothly along the surface. The specified data allow to accept following possible limits of variable parameters of the ground model: for regolith, , , and for bedrocks,.

3. The Reflection Coefficient

We introduce the reflection coefficient F. It equals to the ratio of the radio wave field strength between tracks “Earth - reflected site - satellite A” and “Earth - satellite”. F is represented by two factors:

(3)

where T is the reflection coefficient of the field strength from a smooth sphere with a high conductivity, M is a module of the complex reflection coefficient of a radio wave from the plane boundary. This boundary is the tangent to the sphere in reflecting point. Here we discuss horizontally polarized wave. The first factor in the expression (3) is determined with increasing the cross sectional area when beam is reflected from the sphere. Тhe coefficient T depends only on the incidence angle and is described by the relationship:

(4)

Derivation of this expression can be found in some books, e.g. in [17] . The second factor depends on the parameters of a stratified ground model and wavelength. For the calculation of the radio wave complex reflection coefficient from a stratified medium shown to Figure 2 the well-known expression is used:

(5)

Here is the Fresnel complex reflection coefficient from boundary between the vacuum and the regolith:

(6)

is the Fresnel complex reflection coefficient from boundary between the regolith and the bedrock:

(7)

In relationships (6) and (7) we introduce the complex refractive indices for regolith and for bedrock. The angle of radio wave incidence on the bedrock is related with the incidence angle on the regolith by the Snell’s law as shown in Figure 2:

(8)

We are interested in the module of the reflection coefficient of a radio wave field strength in the site of the lunar surface, which is determined by the following expression with taking relationships (5) and (8) into account:

(9)

Components of the formula (9) are given by relations (6)-(8) and the following expressions:

(10)

(11)

The Fresnel coefficients arguments in (6) and (7) are denoted as and

, where and are real parts of the complex reflection coefficient, and are the imaginary ones. Numerical analysis shows that in (11) the expressions in the brackets are so small, that. The factor indicates the phase relations of radio waves reflected from the boundaries between the media 0 and 1, 1 and 2, and the value of is connected with the absorption of waves in a regolith.

Equation (9) has two asymptotic solutions. At factor M(η) is approximated by M₁(η), i.e. radio wave is reflected from the regolith surface, and the presence of bedrock is not shown. Putting l_max = 15 m and tan d₁ = 4 ´ 10⁻², we find that this is possibly only at case of centimeter radio waves. Other asymptotic solution is fairly obviously: at M(η) converges to M₂(η), i.e. wave reflected from the rock, not feeling the regolith. In all other cases, the dependence M(η) is an oscillating function. The position of the local extremes of the function M(η) and their number when changing η in the range from 0˚ to 90˚ is given by formula

(12)

where m―the integer 1, 2, …It follows from (12) that the reflection coefficient is a multi-valued function, even for fixed values of λ, and η. The value M in this case depends on the regolith thickness and losses therein.

Using the model of the lunar ground, and the expressions (6) - (11) we analyze dependence of factor F on the layer thickness regolith l, the wavelength and the angle for 100 km satellite altitude. In our case, when reflection of radio waves from the two boundaries of subsurface is significant, the dependence F on the ratio of regolith layer thickness and the wavelength gets the oscillatory character. Figure 3 shows the dependence on the reflection coefficient F as function of the regolith layer thickness for, , and the angle. The graphics A, B and C correspond to a wavelength, and. Note that the horizontal scale is different for these graphs.

According to (9), the upper and the lower envelope curves of the oscillations are determined

with the formulas:

(13)

(14)

Values and depend on the loss tangent and wavelength. In the decimeter range, with increasing layer thickness l, the difference between and decreases (Figure 4(c)) and when l = 10 − 15 m oscillations disappear. If the thickness of the regolith layer in the direction of motion of the reflecting point is changed, a periodic fluctuation of the reflected signal level should appear. The period of such variations

, where is velocity of moving point D on the surface. At variations of a

radio wave incidence angle oscillations dependence should also be observed. Figure 4 shows the dependences of for three wavelengths: curves B and C correspond to and respectively, and the curve A is given for. It is seen that in the meter band the oscillations are great, and decameter oscillations absent. These curves are drawn at and the same ground parameters, , , as in Figure 3. The reflection coefficient F decreases rapidly when due to the influence of the factor T.

4. Determination of Ground Parameters

The regolith layer thickness, the density and dielectric parameters of a rocks must be are reconstructed using the experimental values of the reflection coefficient F. Formulae (3) and (4) show that the measured values of the reflection coefficient allow to calculate M = F/T, which is the reflection coefficient from plane-layered ground. The reflection coefficient M is connected with regolith and bedrock parameters by the complex relationship (9). Using a digital map of the Moon we choose a relatively flat region, for which the Rayleigh law is correct:

(15)

where is the standard deviation of the heights of surface roughness from the plane.

We assume that long-term operation of the lunar satellite receiver creates a large array of reflection coefficient measurements at different incidence angles. Such array can be obtained for three radio bands: in decameter, meter and decimeter bands.

Let us now consider the method for determination of the dielectric constant of the regolith. For the decimeter waves the oscillations of M will be weakly or absents. It indicates that there is the strong radio wave absorption. In this case, the influence of the medium 2 can be neglected (Figure 3(c)) and the average experimental value corresponds to the expression (6) for the radio waves reflection from the boundary between the medium 0 and 1. If the regolith dielectric permittivity, than can be determined from formula (6) as

(16)

Using this value and the formula (2) we may determine the regolith density.

We present a procedure for determining the thickness of the regolith l . For this aim, we use the results of measurements of the reflection coefficient of radio waves in meter band and value defined as described above. We choose a pair of experimental values and so that the angles of incidence differed not very strongly, e.g., within 3˚, and the difference between the values and was as much as possible. For example, such a situation is shown on Figure 4 by points 1 and 2. Each of the values is

connected with the functions , and by the formula (9). The

Fresnel reflection coefficients from the boundary between vacuum and regolith and are calculated with the formula (6) using the value for angles and. For the accepted model of ground the numerical analysis showed that, the function changed little when the incidence angles changed in the range of 10˚. For the selected angles and this function can be considered as constant. We denote the function as X . Taking into account the above notation, the formulae (9)-(11) and the condition we can write the system of two equations:

(17)

which depends on two unknown X and l. l is a multiplier in. The equations system (17) is reduced to the form:

(18)

Here L₁, , , , and are the values depending on, , , as follows:

From the equations system (18) we obtain:

. (19)

Substituting (19) into the first equation of system (18) gives the equation relating and :

(20)

This equation depends on one unknown l , it is solved numerically. The solution is the minimal value, when (20) is correct.

In order to determine the imaginary part of the regolith refractive index, it is necessary to take two measured values in the decameter band additional for the pair of radio wave reflection coefficients of meter range. The two sets must satisfy the conditions of the described above procedure. For each pair the equations (18) must be solved. For reconstruction the solutions of the system (18) and and values and l recovered above are used. The ratio to gives the following equation:

(21)

where the unknown is a multiplier in . It is determined by the formula

(22)

The reflection coefficient from the boundary “regolith - bedrock” can be determined using the formula (9) and reconstructed values, and l . It allows to find the real part of the bedrock refractive index. This value follows from the formula (7):

. (23)

The density of the bedrock is calculated with the formula (2).

For decameter waves, the interference changes of the reflection coefficient can be observed in some regions with a horizontal gradient of the regolith thickness. In this case, it is possibly to measure their maximum and minimum values. If we can neglect the influence of small absorption of radio waves in regolith and, according to (13), (14), we assume that

(24)

(25)

Here and are Fresnel reflection coefficients (6) and (7), but and are the real parts of the refractive index of the regolith and bedrock. Using the experimental values close to maxima and minima of the reflection coefficients in equations (24) and (25) allows to determine и , and after them from Fresnel formulas to restore and.

Registration of oscillations of reflection coefficient for meter or decimeter radio waves in the region with the horizontal gradient permits to determine the absorption of radio waves in the regolith. This method of the absorption detection is based on the analysis of decreasing function with increasing l, as shown at Figure 3 by curves A and B. If we define that the number of registered maximums of the reflection coefficient is equal and take into account that, according to (12), the total change of the thickness of the regolith in probing site is , then the absorption coefficient in the regolith may be determined.

Discussed principles of the inverse problem solving of sensing subsurface layer are the basis for the creating a multi-stage algorithm for determining, , , , and l. Testing real algorithm for determining ground parameters requires the use of experimental data of the reflection coefficient of radio waves for different angles of incident .

5. Conclusion

The method of bistatic subsurface sounding allows measuring the reflection coefficient of the radio waves with high accuracy. It is possible because the reflection coefficient is a ratio of the field strengths of the direct and reflected from the Moon radio waves. The relative measurement of the amplitudes of these signals may be due to their frequency separation. In this case, the possibly variations of the transmitter power, receiver gain and the effects of the Earth’s ionosphere do not affect the accuracy of the measurements. The transmitter location on the Earth provides much greater signal power compared with transmitter located at the satellite. It provides a deeper penetration of radio waves in the subsurface. The sizes of reflecting spots on the lunar surface depend on satellite height, wavelength and an incidence angle of radio waves. For height, and in a plane of incidence radio wave and in a perpendicular direction they are approximately, and when 50˚ − 70˚ they increase to 5 km. In this work, the features of the reflection of radio waves from the lunar ground have been discussed. The method of ground parameters reconstruction has been described in detail.

Using both bistatic and monostatic modes of radio location improves the accuracy and reliability of the research results. The possibilities of a monostatic location of the subsurface with receiver and transmitter located on the lunar satellite are given in papers [1] , [24] . The monostatic mode allows exploring the ground parameters both on visible and internal side of the Moon and―what is important―in polar areas. Radar, combined in one hardware complex and using the two methods, would provide detailed high-precision measurements for determination of the distribution of ground parameters in various regions of the Moon.

Acknowledgements

We thank A.I. Efimov, whose comments helped improve this manuscript. The work has been supported by the Program № 9 “Experimental and theoretical studies of objects in the solar system and planetary systems of stars” of the Presidium RAS and partially by Grant of Russian Fund for Basic Research RAS № 13-02-00526.

Cite this paper

Oleg I.Yakovlev,Olga V.Yushkova,Stanislav S.Matyugov,Alexander G.Pavelyev,Vladimir M.Smirnov, (2015) Determination of the Lunar Ground Characteristics Using Bistatic Radar. International Journal of Geosciences,06,1267-1276. doi: 10.4236/ijg.2015.612101

References