International Journal of Geosciences
Vol.05 No.12(2014), Article ID:51407,10 pages
10.4236/ijg.2014.512115
Interpretation of Gravity Anomalies by Multi-Scale Evaluation of Maxima of Gradients and 3D Modelling in Bipindi Region (South-West Cameroon)
Fidèle Koumetio1,2*, Donatien Njomo1, Constant Noutchogwe Tatchum1,3, Alain Pierre Kamga Tokam4, Tabod Charles Tabod1,3, Eliezer Manguelle-Dicoum1
1Department of Physics, Faculty of Science, University of Yaounde I, Yaounde, Cameroon
2Department of Physics, Faculty of Science, University of Dschang, Dschang, Cameroon
3Department of Physics, University of Bamenda, Bamenda, Cameroon
4School of Geosciences, University of Witwatersrand, Johannesburg, South Africa
Email: *koumetiof@yahoo.fr
Copyright © 2014 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 14 September 2014; revised 8 October 2014; accepted 4 November 2014
ABSTRACT
The gravity maps display, in Bipindi zone, local oval culminations of low anomalies indicative of a presence of intrusive light body in a subsurface but the nature, the form and the position of this body are still unknown. The analyses of established gravimetric anomaly maps, the multi-scale evaluation of maxima of gradients and the quantitative interpretation of residual anomalies by 3D modelling permit characterizing the intrusive light body situated at Bipindi. The multi-scale evaluation of maxima of gradients shows that the modelling of the intrusive light body of Bipindi can be done without the problem of interference of anomalies from different sources. The 3D model of Bipindi zone shows two dissymmetrical blocks of the same type of rock with a density contrast of −0.095 g∙cm−3 in comparison with the density of the surrounding metamorphic rocks. The two blocks are at a distance about 3 km from one to another. The upper surfaces of these blocks lie at a depth between 1 and 2 km. Their lower surfaces have two landings; one lies at a depth of about 8 km and another at a depth about 14 km. A consideration of the density of the modelled body, of the ranges of densities of specific rocks present in the general region indicates that the body may be composed of nepheline syenites. The intrusive body of Bipindi is situated in a senestral shear zone. The area situated between the two blocks of this intrusive body may be indicated for a detail study in the domain of mineral research.
Keywords:
Gravity Anomalies, Maxima of Gradients, Residual Anomalies, Modelling

1. Introduction
The study area is located between latitudes 2˚50'N - 3˚28'N and longitudes 10˚20'E - 10˚45'E (Figure 1). The green rock belts (GRB) and gneiss are part of a geological unit called “Nyong Unit”. They cover a greater part of the study area. The other part of the study area is covered by charnockites which are part of a geological unit called “Ntem Unit”. The gravity maps (Figure 2 and Figure 3) display, in our study area, local oval culminations of low anomalies indicative of a presence of intrusive light body in a subsurface. The comparison of the geological and gravity maps shows that this intrusive light body is situated in the Nyong Unit. This comparison cannot permit identifying the nature of the body which provokes the observed anomalies. The works of many authors [1] - [9] attest that the intrusive rocks founded in the Nyong Unit are alkaline syenite, nepheline syenite, granite, dolerite and peridotite. At this stage, the nature, the form and the position of the intrusive light body responsible for the observed anomalies are still unknown.
In this paper, we propose to characterize the intrusive body responsible for the negative anomalies observed in our study area by the multi-scale evaluation of maxima of the horizontal derivative of the vertical gradient of the Bouguer anomaly and by 3D modelling.
2. Geological and Tectonic Setting
A smaller part of our study area is covered by the geological formations of Ntem Complex which is the northern portion of the Congo Craton in Cameroon. The Ntem Complex is composed mainly by Archean rocks [10] that include intrusive rocks, leptynites and gneisses. Granites, tonalites and syenites are the main intrusive rocks seen in the Ntem Complex.
Figure 1. Location and simplified geological map of the region [3] [11] . Basins of the Atlantic coast of Cameroon: 1: Sediments. Nyong Unit: 2: Gneiss; 3: Metagranodiorite; 4: Metamorphic rocks of the Yaounde Group; 5: Green rock belts. Ntem Unit: 6: Charnockites; 7: Green rock belts; 8: Banded series; 9: Tonalites; 10: Potassic granitoïdes. Yaounde Group: 11: Metamorphic unit of the panafrican north equatorial chain; 12: Fault; 13: Study area.
Figure 2. Bouguer anomaly map of the region showing the study area.
Figure 3. First order residual anomaly map of the region sh- owing the study area.
The study area is constituted predominantly of formations of the Nyong Unit. This Unit corresponds to the remobilized NW edge of the Ntem Complex [3] [4] [8] . Gneisses and green rock belts (GRB) are the main formations of our study area (Figure 1). The GRB is composed by ferriferous and barren quartzites, basic and ultrabasic rocks. According to Maurizot et al. [3] , a faulting deformation has been responsible of development of blastomylonitic shear zones which appear irregularly on the whole Nyong and Ntem Unit. Nsifa [11] mentioned that the last magmatic episode in the Nyong Unit corresponds to the Neoproterozoic intrusion of nepheline syenite in a sinistral shear zone.
A seismological study in all the Cameroonian territory by Tokam et al. [12] shows that the thickness of the upper crust is variable and ranges in general between 10 and 20 km. The gravimetric modelling along a SW-NE profile passing through Kribi and Lolordorf shows that the thickness of the upper crust is approximately equal to 18 km [13] [14] . Owona Angue et al. [13] present a 2D model of resistivity according to a profile which begins substantially at the end of the SW negative gravity anomaly contours of Bipindi (Figure 3) and covers 3/4 of the anomaly zone in the direction of the NE-SW elongation. This 2D resistivity model has two resistant blocks separated by the less resistant rocks. Both resistant blocks have roofs mainly located at a depth of approximately 1 km and bases located mostly at a depth of about 14 km. A small portion of each block has its top at a depth of about 2 km. Going up from the base, the east end of the block West takes the direction SW-NE while the West end of East block takes the SE-NW direction, indicating in each case, a gradual decrease of the depth of the base from 14 km to a depth of about 8 km.
3. Processing and Interpretation of Gravity Data
3.1. Gravity Anomaly Maps
The gravity data used in this work were collected during gravity surveys of Central Africa, by ORSTOM and referenced in [15] , completed later by surveys of Princeton University in 1968, University of Jos in 1975, University of Leeds in 1982, University of Ibadan from 1984 to 1986, IRGM and University of Leeds from 1984 to 1988 referenced in [16] . The data were collected with a station-spacing of 3 to 5 km and the gravimeters used were Lacoste & Romberg (model G, n˚ 471 and 823), Worden (n˚ 69, 135, 313, 600 and 1153), World Wide (n˚ 36), Canadian Scintrex (n˚ 305 G) and North-American (n˚ 124 and 165). The Bouguer anomaly values were computed using a mean crustal density of 2.67 g/cm3.
The Bouguer anomaly data contains the combined effects of the deep and large basement structures and the shallow sediment layers with limited lateral extension. The polynomial fitting method is used to separate the Bouguer anomaly into its regional and residual components. This method computes the mathematical surface which gives the best fit to the gravity field within specific limits [17] . This surface is considered to be the regional gravity anomaly. The residual is obtained by subtracting the regional field from Bouguer anomaly. Practically, the regional of order n is assimilated to a polynomial of n degree. For smaller n, there exist a relative important gap between the regional anomaly and the Bouguer anomaly. With the progressive increase of the polynomial order, the regional anomaly became progressively closer to the Bouguer anomaly revealing, through corresponding residual anomaly, geological structures which are more and more closer to the surface. The gravity data obtained are interpolated using the Kriging method and the spacing of the grid points is 2 km along each axis. The gravity anomaly maps were obtained by an automatic computer drawing from the established grids using a contour interval of 3 mGal (Figure 2 and Figure 3).
The Bouguer and residual anomalies maps show, in the study area (Figure 2 and Figure 3), negative isogals having a ring shape indicative of a presence of intrusive light body in a subsurface. The low gravity ascribed to a low density intrusion is visibly more distinct on the residual gravity map. On this residual map, the isogals mentioned above are extended northeastward showing that the lengthening axis of the intrusive body is oriented SW-NE. We used the first order residual anomalies for modelling in order to have a better chance of locating the bottom of the intrusive light body earlier mentioned. As a matter of fact, the effect of this intrusive body is observed on the Bouguer anomaly map (Figure 2) but the first order residual anomalies are used because we are not interested in the effects of the mantle and lower crust.
By comparison of the geological map with the first order residual anomaly map (Figure 1 and Figure 3), we can see that the intrusive light body is in a zone occupied by gneiss and green rocks on the geological map. Knowing that the green rocks are generally the metamorphic form of basic and ultrabasic rocks, we can say that the intrusive light body of Bipindi is surrounded by an assembly of metamorphic rocks. The interval of variation of density of metamorphic rocks is from 2.4 to 3.1 g/cm3 [18] . We assume that the average density of the assembly of metamorphic formations in the study area is equal to 2.67 g/cm3 because the Bouguer anomaly values were computed using a mean crustal density of 2.67 g/cm3 (this means that the anomaly produced by this assembly of metamorphic formations is zero). We can see on the first order residual anomaly map (Figure 3) that there are dense bodies in Lolodorf and around the Kribi-Dehane axis but we don’t want that the effect of these bodies influence the modelling. We will then use only the negative values of anomalies taken in the study area to be sure that they are provoked by the intrusive light body alone.
3.2. Multi-Scale Analysis of Maxima of Gradients
The maxima of the horizontal gradient of the vertical derivative of Bouguer anomalies help locate contacts associated with abrupt changes in density and the multi-scale analysis of these maxima involves upward continuation of the gravity field to different heights with a view to characterize the vertical extension of anomalous structures [19] - [22] . Faults are expressed by a quasi-linear disposition of many maxima and horizontal limits of intrusive bodies are showed by quasi-circular disposition of many maxima. The multi-scale analysis was done by determining:
· The upward continued field at different heights h. We have used the Fourpot program to calculate the upward continuation [23] . The maximum value to give to h is taken to be equal to the optimum upward continuation height ho of the gravity field [22] . Using the gravity data of the Sud-ouest Cameroon, Koumetio et al. [24] have shown that the optimum upward continuation height of this region is ho = 35 km.
· The vertical derivative at different heights. Given gv to be the vertical derivative of potential field g at height h, it is calculated in the space domain using the method of finite differences proposed by Florio et al. [25] . This method allows the calculation of vertical derivative at several heights, using a stable operator like upward continuation [26] . The Formula (1) is used to calculate gv
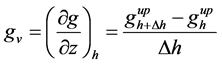 (1)
(1)
where  is the field upward continued at the height h and
is the field upward continued at the height h and  is the field upward continued at a slightly higher level
is the field upward continued at a slightly higher level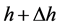 .
. 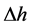 is a small height difference lying between 1/10 and 1/100 of the data sampling interval [22] . We have taken Δh = 0.5 km.
is a small height difference lying between 1/10 and 1/100 of the data sampling interval [22] . We have taken Δh = 0.5 km.
· The horizontal gradient of the vertical derivative and its local maxima. Given gHV to be the horizontal gradient of the vertical derivative at a height h; its value is calculated in the spatial domain using the formula (2):
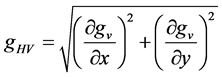 (2)
(2)
where gv is the vertical derivative of potential field g at height h as defined in relation (1). The positions of local maxima are determined by the Blakely and Simpson method [27] . The horizontal gradients and their maxima were calculated using the BOUNDARY program of the Fortran 77 package of the United States Geological Survey [28] .
The superposition of local maxima of horizontal gradient determined on the vertical derivative of the Bouguer anomalies upward continued at the heights 5 km, 10 km, 15 km, 25 km and 35 km help in the realization of the map shown in Figure 4. This map shows, in our study area, a quasi-circular contact (noted c11) corresponding to horizontal limit of the intrusive body of Bipindi. The map of maxima (Figure 4) shows that the intrusive body of Bipindi is far from that of Pouma, which is not quite visible on the residual anomalies map of order 1 (Figure 3). Thus, the modelling of (c11) can be done without the problem of interference of anomalies from different sources.
According to Koumetio et al. [24] , the depth of the top of the anomaly sources obtained after an upward continuation at the height h is superior or equal to  because the upward continuation at the height h eliminates the effect of the sources situated above the depth
because the upward continuation at the height h eliminates the effect of the sources situated above the depth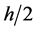 . Thus, the blue maxima (Figure 4) indicate that the effects of the sources situated above the depth 2.5 km are eliminated. This depth becomes 5 km for green maxima, 7.5 km for yellow maxima, 12.5 km for magenta maxima and 17.5 km for red maxima. Therefore, we can understand for example that the presence of blue, green and yellow maxima on the same contact with the absence
. Thus, the blue maxima (Figure 4) indicate that the effects of the sources situated above the depth 2.5 km are eliminated. This depth becomes 5 km for green maxima, 7.5 km for yellow maxima, 12.5 km for magenta maxima and 17.5 km for red maxima. Therefore, we can understand for example that the presence of blue, green and yellow maxima on the same contact with the absence
Figure 4. Superposition of the maxima of the gradients computed at various heights of upward continuation. Maxima are represented by small colored squares. The blue, green, yellow, magenta and red colors represent the maxima of the gradients upward continued at the heights 5 km, 10 km, 15 km, 25 km and 35 km respectively.
of magenta and red maxima indicates that the depth of its bottom is between 7.5 and 12.5 km. We can also understand for a second example that the presence of blue maxima on one contact with the absence of other maxima colours indicates that the depth of its bottom is between 2.5 and 5 km.
In Figure 4, the analysis of colours of maxima presents on the contour of the intrusive body (c11) shows that the NE and the SW parts of c11 extent until a depth lying between 12.5 km and 17.5 km (parts marked by blue, green, yellow and magenta maxima) while its centre part extent until a depth lying between 7.5 km and 12.5 km (part marked by blue, green and yellow maxima).
3.3. Direct Modelling
We used the gravity modelling program GRAV3D [29] to obtain the 3D model of the intrusive body (c11) of Bipindi. In order to take into account all the constraints that are the results of Owona Angue et al. [13] (2D model of resistivity described in paragraph 2: two resistant blocks each having roofs at 1 and 2 km and bases at 8 and 14 km), we chose to construct the intrusive body c11 and compare the anomaly calculated by the program GRAV3D to the experimental anomaly.
The program GRAV3D offers the possibility to construct one body using bricks which can be the rectangular parallelepipeds of different dimensions. Each brick has a constant density contrast. The dimensions of one brick must be given along two horizontal axes (Ox, Oy) and one vertical axis Oz. The coordinates (xo, yo, zo) of the origin point O must be indicated as well as the minimal variations ∆x, ∆y and ∆z along each axis.
In the case of the intrusive body of Bipindi, we tested several values of density contrast and we selected the value of −0.095 g/cm3 for each brick. The origin 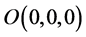 is the point of latitude 9˚55'E and of longitude 2˚24'N which is already the origin on the residual anomalies map (Figure 3). It is in comparison to the origin O that the coordinates of each point are given along the axes Ox of latitudes, Oy of longitudes and along the vertical axis Oz.
is the point of latitude 9˚55'E and of longitude 2˚24'N which is already the origin on the residual anomalies map (Figure 3). It is in comparison to the origin O that the coordinates of each point are given along the axes Ox of latitudes, Oy of longitudes and along the vertical axis Oz.
The data taken in the study area allowed the program GRAV3D to generate experimental map shown on Fig- ure 5. Taking into account all the constraints mentioned above we constructed the 3D model of c11 brick by brick. We enter the following data in the program GRAV3D:
Figure 5. Experimental residual anomaly map of the Bipindi area. The black spots represent the data points.
xo = 26,400 m, yo = 37,500 m, zo = 0, ∆x = ∆y = 3000 m, ∆z = 1000 m
Brick 1: 35,400 ≤ x ≤ 41,400 m; 67,500 ≤ y ≤ 88,500 m; −14,000 ≤ z ≤ −2000 m
Brick 2: 41,400 ≤ x ≤ 50,400 m; 67,500 ≤ y ≤ 82,500 m; −14,000 ≤ z ≤ −2000 m
Brick 3: 50,400 ≤ x ≤ 53,400 m; 61,500 ≤ y ≤ 112,500 m; −8000 ≤ z ≤ −1000 m
Brick 4: 56,400 ≤ x ≤ 59,400 m; 58,500 ≤ y ≤ 112,500 m; −8000 ≤ z ≤ −1000 m
Brick 5: 59,400 ≤ x ≤ 62,400 m; 58,500 ≤ y ≤ 100,500 m; −8000 ≤ z ≤ −1000 m
Brick 6: 62,400 ≤ x ≤ 77,400 m; 76,500 ≤ y ≤ 112,500 m; −8000 ≤ z ≤ −1000 m
Brick 7: 77,400 ≤ x ≤ 86,400 m; 88,500 ≤ y ≤ 112,500 m; −14,000 ≤ z ≤ −2000 m
Brick 8: 77,400 ≤ x ≤ 86,400 m; 88,500 ≤ y ≤ 97,500 m; −2000 ≤ z ≤ −1000 m
The calculated map obtained (Figure 6) can be superposed approximately to the experimental map. The 3D model obtained (Figure 7) shows globally two dissymmetrical blocks of the same type of rock separated on a distance of about 3 km. The axis of separation has an N-S direction. The intrusive body of Bipindi has two landings of roofs at the depths of about 1 km and 2 km. The underside view of the 3D model (Figure 8) shows two landings for the bottom of c11, one is at a depth of about 8 km and another is at a depth of about 14 km.
4. Discussion
The 3D model of the intrusive body of Bipindi obtained is in accordance with the results of the multi-scale analysis of maxima of gradients. Indeed, the depth of 8 km for the base of the central portion of (c11) is in the range provided by the multi-scale analysis of maxima of gradients (range of 7.5 km to 12.5 km). Similarly, the depth of 14 km for the bases of the outermost parts of (c11) is in the range of 12.5 km to 17.5 km.
The disposition of the two blocks of the intrusive body of Bipindi along the axis of separation lets us think to a senestral shear zone. This is in accordance with the result of Maurizot et al. [3] which stipulate that a faulting deformation has been responsible of development of blastomylonitic shear zones which appear irregularly on the whole Nyong and Ntem Unit. We think finally that the characterization of the intrusive body of Bipindi is founded entirely in the results of Tchameni et al. [10] and Shang et al. [30] which mention that this zone has been affected by a polyphasis deformation which put in place a vertical foliation in the relic of green rocks belt, a senestral shear with partial smelting and later dynamic quartzitic recrystallizations.
Figure 6. Calculated anomaly map of the Bipindi area. The black spots represent the data points.
Figure 7. 3D model of the intrusive body of Bipindi (the north side view).
We assumed that the average density of the metamorphic formations in the study area is equal to 2.67 g/cm3 then the density of the intrusive body of Bipindi can be evaluated at about 2.57 g/cm3 knowing that the density contrast is −0.095 g/cm3. We give in Table 1 the different intrusive rocks founded in the study area and the range of variation of density of each type [18] .
Given all this, the intrusive body obtained by gravity modelling may be composed of nepheline syenites or granites. It is more likely that (c11) is composed of nepheline syenites because Nsifa [11] mentioned that the last magmatic episode in the Nyong Unit corresponds to the Neoproterozoic intrusion of nepheline syenite in a sinistral shear zone.
We know that there are more often than not transport and accumulation of mineralized substances in the deformation zones and mainly in shear zone. Then the localization of deformation belts between the two blocks of the intrusive body of Bipindi can be a guide for mineral prospection.
Table 1. Different intrusive rocks founded in the study area and the range of variation of density of each type.
Figure 8. 3D model of the intrusive body of Bipindi (the underside view).
5. Conclusion
The analyses of established gravity anomaly maps, the multi-scale evaluation of maxima of gradients and the quantitative interpretation of residual anomalies by 3D modelling suggest the presence of an intrusive light body situated at Bipindi. The multi-scale evaluation of maxima of gradients shows that the modelling of the intrusive light body of Bipindi can be done without the problem of interference of anomalies from different sources. It also shows that the NE and the SW parts of this intrusive body extend until a depth lies between 12.5 km and 17.5 km while its centre part extends until a depth lies between 7.5 km and 12.5 km. The 3D model of Bipindi zone shows two dissymmetrical blocks of the same type of rock with a density contrast of −0.095 g∙cm−3 in comparison with the density of the surrounding metamorphic rocks. The two blocks are at a distance of about 3 km from one to another. The upper surfaces of these blocks lie at a depth of between 1 and 2 km. Their lower surfaces have two landings; one lies at a depth of about 8 km and another lies at a depth of about 14 km. The 3D model of the intrusive body of Bipindi obtained is in accordance with the results of the multi-scale analysis of maxima of gradients. A consideration of the density of the modelled body, of the ranges of densities of specific rocks present in the general region indicates that the body may be composed of nepheline syenites. The intrusive body of Bipindi is situated in a senestral shear zone. The area situated between the two blocks of this intrusive body may be indicated for a detail study in the domain of mineral research.
Acknowledgements
This paper benefits from the fruitful criticism and suggestions by three anonymous reviewers, leading to an improvement of the work. They are gratefully acknowledged.
References
- Bessoles, B. and Lasserre, M. (1977) Le complexe de base au Cameroun. Bulletin de la Société Géologique de France, 19, 1085-1092.
- Bessoles, B. and Trompette, R. (1980) Géologie de l’Afrique: La chaîne panafricaine, zone mobile d’Afrique Centrale (partie Sud) et zone soudanaise. Mémoire BRGM No. 92.
- Maurizot, P., Abessolo, A., Feybesse, J.L., Johan, V. and Lecomte, P. (1986) Etude et prospection minière du sud- ouest Cameroun. Synthèse des travaux de 1978 à 1985. Rapport, BRGM, 274.
- Minyem, D. and Nedelec, A. (1990) Origin and Evolution of the Eseka Gneisses (Cameroon). Archean TTG Reworked in the Panafrican Mobile Belt. 15th Colloquium of African Geology, Vol. 2, Occasional Publication, Nancy, 21-24.
- Minyem, D. (1994) Contribution à l’étude métamorphique et structurale du secteur Eséka-Makak (Cameroun). Thèse de Doctorat 3e cycle, Université de Yaoundé I, Yaoundé, 166.
- Toteu, S.F., Van Schmus, R.W., Penaye, J. and Nyobe, J.B. (1994) U-Pb and Sm-Nd evidence for Eburnian and Pan-African High-Grade Metamorphism in Cratonic Rocks of Southern Cameroon. Precambrian Research, 67, 321- 347. http://dx.doi.org/10.1016/0301-9268(94)90014-0
- Vicat, J.P., Leger, J.M., Nsifa, E., Piguet, P., Nzenti, J.P., Tchameni, R. and Pouclet, A. (1996) Distinction au Sein du craton congolais du Sud-Ouest du Cameroun, de deux épisodes doléritiques initiant les cycles Orogéniques éburnéen (Paléoprotérozoïque) et Pan-Africain (Néoprotérozoïque). Compte Rendu de l’Académie des Sciences, 323, 575-582.
- Tchameni, R. (1997) Géochimie et Géochronologie des formations de l’Archéen et du Paléoprotérozoïque du Sud- Cameroun (groupe du Ntem, craton du Congo). Thèse Doctorat Université d’Orléans, Orléans, 356.
- Vicat, J.P., Nsifa, E., Tchameni, R. and Pouclet, A. (1998) La ceinture de roches vertes de Lolodorf-Ngomedzap (Sud- Cameroun). Pétrologie, géochimie et cadre géodynamique. Géosciences au Cameroun, collect GEOCAM 1/1998, ed. Vicat, J.P. and Bilong, P., Presse Universitaire Yaoundé I, Yaoundé, 325-337.
- Tchameni, R., Mezger, K., Nsifa, N.E. and Pouclet, A. (2001) Crustal Origin of Early Proterozoic Syenites in the Congo Craton (Ntem Complex), South Cameroon. Lithos, 57, 23-42. http://dx.doi.org/10.1016/S0024-4937(00)00072-4
- Nsifa, E.N. (2005) Magmatisme et évolution géodynamique de l’Archéen au Protérozoïque de la bordure nord-ouest du craton du Congo (complexe du Ntem) au Sud-Ouest Cameroun. Thèse Doctorat d’Etat, Université de Yaoundé I, Yaounde, 248.
- Tokam, K.A.P., Tabod, C.T., Nyblade, A.A., Julia, J., Wiens, D.A. and Pasyanos, M. (2010) Structure of the Crust Beneath Cameroon, West Africa, from the Join Inversion of Rayleigh Wave Group Velocities and Receiver Functions. Geophysical Journal International, 183, 1061-1076. http://dx.doi.org/10.1111/j.1365-246X.2010.04776.x
- Owona Angue, M.L.C., Nguiya, S., Nouayou, R., Tokam Kamga, A.P. and Manguelle-Dicoum, E. (2011) Geophysical Investigation of the Transition Zone between the Congo Craton and the Kribi-Campo Sedimentary Basin (South-West Cameroon). South African Journal of Geology, 114, 145-158. http://dx.doi.org/10.2113/gssajg.114.2.145
- Owona Angue, M.L.C. (2012) Investigation géophysique de la zone de transition entre le sous-bassin Sédimentaire de Kribi-Campo et la bordure nord-ouest du Craton du Congo. Thèse Doctorat/Ph.D., Université de Yaoundé I, Yaounde, 120.
- Collignon, F. (1968) Gravimétrie et reconnaissance de la République Fédérale du Cameroun. ORSTOM, Paris, 35.
- Legeley-Padovani, A., Poudjom-Djomani, Y.H., Boukeke, D.B., Nnange, J.M., Ateba, B., Albouy, Y. and Fairhead, J.D. (1996) Levés gravimétriques de reconnaissance du Cameroun. ORSTOM, Paris.
- Radhakrishna, I.V. and Krishnamacharyulu, S.K.G. (1990) Polyfit: A Fortran 77 Program to Fit a Polynomial of Any Order to Potential Field Anomalies. Journal of the Association of Exploration Geophysicists, 11, 99-105.
- Telford, W.M., Geldart, L.P. and Keys, D.A. (1976) Applied Geophysics. Cambridge University Press, Cambridge, 860.
- Cordell, L. (1979) Gravimetric Expression of Graben Faulting in Santa Fe Country and the Espanola Basin, New Mexico. In: Ingersoll, R.V., Ed., Guidebook to Santa Fe Country, New Mexico Geological Society, Socorro, 59-64.
- Cordell, L. and Grauch, V.J.S. (1985) Mapping Basement Magnetization Zones from Aeromagnetic Data in the San Juan Basin, New Mexico. In: Hinze, W.J., Ed., The Utility of Regional Gravity and Magnetic Anomaly Maps, Society of Exploration Geophysicists, 181-197. http://dx.doi.org/10.1190/1.0931830346.ch16
- Noutchogwe, T.C. (2010) Investigation géophysique dans la région de l’Adamaoua par les méthodes gravimétriques et magnétiques: Implications structurales et hydrogéologiques. Thèse Doctorat/Ph.D., Université de Yaoundé I, Yaounde, 147.
- Noutchogwe, T.C., Tabod, C.T., Koumetio, F. and Manguelle-Dicoum, E. (2011) A Gravity Model Study for Differentiating Vertical and Dipping Geological Contacts with Application to a Bouguer Gravity Anomaly over the Foumban Shear Zone, Cameroon. Geophysica, 47, 43-55.
- Pirttijärvi, M. (2009) FOURPOT. University of Oulu, Department of Physics, Oulu. www.cc.oulu.fi/~mpi/Softat/Fourpot.html
- Koumetio, F., Njomo, D., Tabod, C.T., Noutchogwe Tatchum, C. and Manguelle-Dicoum, E. (2012) Structural Interpretation of Gravity Anomalies from the Kribi-Edea Zone, South Cameroon: A Case Study. Journal of Geophysics and Engineering, 9, 664-673. http://dx.doi.org/10.1088/1742-2132/9/6/664
- Florio, G., Fedi, M. and Pasteka, R. (2006) On the Application of Euler Deconvolution to the Analytic Signal. Geophysics, 71, 87-93. http://dx.doi.org/10.1190/1.2360204
- Jacobsen, B.H. (1987) A Case for Upward Continuation as a Standard Separation Filter for Potential-Field Maps. Geophysics, 52, 390-398. http://dx.doi.org/10.1190/1.1442378
- Blakely, R.J. and Simpson, R.W. (1986) Approximating Edges of Source Bodies from Magnetic or Gravity Anomalies. Geophysics, 51, 1494-1498. http://dx.doi.org/10.1190/1.1442197
- Phillips, J.D. (1997) Potential-Field Geophysical Software for the PC. Version 2.2., US Geological Survey Open-File Report 97-725, 34.
- Oldenburg, D.W. and Jones, F.H.M. (2007) Inversion for Applied Geophysics; Learning Resources about Geophysical Inversion. University of British Columbia, Vancouver.
- Shang, C.K., Wolfgang, S., Muharrem, S., Funken, C. and Mvondo Ondoa, J. (2004) Zircon Pb-Pb and U-Pb Systematics of TTG Rocks in the Congo Craton: Constraints on Crust Formation, Magmatism, and Pan-African Lead Loss. Bulletin of Geosciences, 79, 205-219.
NOTES
*Corresponding author.











