International Journal of Geosciences
Vol.5 No.4(2014), Article ID:45043,8 pages
DOI:10.4236/ijg.2014.54036
“In Space” or “As Space”?: Spatial Autocorrelation Properties of the Earth’s Interior
Charles H. Smith
Center for Biodiversity Studies, Western Kentucky University, Bowling Green, KY 42101, USA
Email: charles.smith@wku.edu
Copyright © 2014 by author and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/


Received 11 September 2013; revised 13 October 2013; accepted 12 November 2013
Abstract
In this analysis, natural systems are posed to subsystemize in a manner facilitating both structured information/energy sharing and an entropy maximization process projecting a three-dimensional, spatial outcome. Numerical simulations were first carried out to determine whether n × n input-output matrices could, once entropy-maximized, project a three-dimensional Euclidean metric. Only 4 × 4 matrices could; a small proportion passed the test. Larger proportions passed when grouped random patterns on and within twoand three-dimensional forms were tested. The pattern of structural zonation within the earth was then tested in analogous fashion using spatial autocorrelation measures, and for three time periods: current, 95 million years b.p. and 200 million years b.p. All expected results were obtained; not only do the geometries of zonation project a three-dimensional structure as anticipated, but also do secondary statistical measures reveal levels of equilibrium among the zones in all three cases that are nearly total, distinguishing them from simulations that do not incorporate a varying-surface zone-width element.
Keywords: Entropy Maximization, Earth’s Interior, Spatial Autocorrelation, Benedict de Spinoza, Spatial Extension, Space

1. Introduction
In 1894, the British naturalist Alfred Russel Wallace (1823-1913) made the following surprising reply to an ongoing public discussion in the magazine Light as to whether there might be a fourth dimension:
Sir, —The discussion on this subject seems to me to be wholly founded upon fallacy and verbal quibbles. I hold, not only that the alleged fourth dimension of space cannot be proved to exist, but that it cannot exist. The whole fallacy is based upon the assumption that we do know space of one, two, and three dimensions. This I deny. The alleged space of one dimension—lines—is not space at all, but merely directions in space. So the alleged space of two dimensions—surfaces—is not space, but only the limits between two portions of space, or the surfaces of bodies in space. There is thus only one Space—that which contains everything, both actual, possible, and conceivable. This Space has no definite number of dimensions, since it is necessarily infinite, and infinite in an infinite number of directions. Because mathematicians make use of what they term “three dimensions” in order to measure certain portions of space, or to define certain positions, lines, or surfaces in it, that does not in any way affect the nature of Space itself, still less can it limit space, which it must do if any other kind of space is possible which is yet not contained in infinite Space. The whole conception of space of different dimensions is thus a pure verbal fantasy, founded on the terms and symbols of mathematicians, who have no more power to limit or modify the conception of Space itself than has the most ignorant schoolboy [1] .
While this perspective may not quite satisfy today’s mathematicians or physicists, it is yet true that the question of why spatial extension is three-dimensional (at least, in a mesoscale sense) has never been resolved [2] -[8] . In the 1980s the author began looking into this matter, in 1986-1987 publishing a pair of related papers [9] [10] based on an interpretation of part of the natural philosophy of the Rationalist philosopher Benedict de Spinoza (1632-1677). Through Spinozian thinking, it was argued that spatial extension might be based on some properties of internal, subsystem-level, organization common to all naturally evolving systems. This work, followed by years of on-and-off-again simulation and empirical studies, leads to the suggestion that all spatially-extended systems may partition into, specifically, four structurally functional subsystems—the standing interactions among which project as “physical space”. Another way of putting this is to pose that “space” is entropy maximization: not merely because all things “within it” are dissipating according to the Second Law, but additionally because of the way that dissipation is mediated by subsystemization properties common to its all constituent systems.
There are several reasons for not dismissing this foreign-sounding notion out of hand. First, it appears not to seriously conflict with more conventional ways of studying natural structure—that is, positivist/empiricist/mathematical approaches dwelling more on topology and/or causal sequences occurring between systems [4] -[8] [11] -[15] . Second, it has intuitive appeal to the degree that it portrays an evolving space in which previously evolved structures strongly influence the likelihood of later ones evolving. Third, it takes a minimum of four non-coplanar points to specify a three-dimensional Euclidean geometry—an exploitable conceptual relation. Fourth, there is usually considered to be just four elemental forces: gravity, electromagnetism, strong nuclear forces, and weak nuclear forces—whose interactions to form complex structures might possibly be understood in this context. Fifth, it answers Wallace’s objections, given earlier, by providing a more general model of “space” from which three-dimensionality may be seen as one particular outcome. Sixth, it is amenable to simulation approaches, as I will show in a moment. Last, it is also amenable to empirical validation efforts. I have already published one such study [16] —an analysis of the physiographic geometry within thirty-one stream basins; this seems to expose the kind of relationships posed. In the present work another application, this one to the interior geo-structural zones of the earth, is shown to relate to the model as well.
If the systems that comprise extended space are in fact organized in the manner
I postulate, it seems a priori likely that they must exhibit some kinds of evidence
of structure related to energy transfer and dissipation in the way suggested. These
can be expected to stand as nonrandom patterns of differentiation in observable
space, and therefore should be amenable to study through forms of pattern analysis.
In particular, the patterns involved should reflect an entropy maximization process
that sustains three-dimensionality itself; this is a difficult thing to envision,
but reduces to the idea of a balance, as expressed in three dimensions, among its
subsystems. One possible first step toward describing this organization is to conceive
of a simple n by n flows/similarities matrix representing the summary characteristics
of internal information flow (or sharing) such a system might exhibit: that is,
as an i=1,n, j=1,n input-output matrix. Given such a numerical representation, the
central question becomes whether the relations within any structures described in
this fashion can be shown to project unambiguously as a three-dimensional space.
Otherwise stated, will group-level interrelations (i.e., among a system’s primary
subsystems, whether these be discretely separated from one another, or more complexly
interlocated) reveal a cryptic Euclidean dimensionality to their fundamental organization?
This question can be answered in a technical sense by subjecting related i=1,n,
j=1,n data to a metric multidimensional scaling (MDS) operation: where an unambiguous
solution in three dimensions is produced such that x1 + x2
+
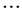 xn = 0, y1 + y2 +
xn = 0, y1 + y2 +
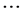 yn = 0, and z1 + z2 +
yn = 0, and z1 + z2 +
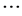 zn = 0, each i = 1, n vector of relations contributing equally, ipso
facto, to the group (spatial) structure. Ordinarily MDS is used to probe for internal
structure within a set of similarities (or analogous) data. In such efforts the
dimensional representation serves a similar purpose to the number of factors arriving
in factor analysis. Here, however, we anticipate something more than just unambiguous
representation as a three-dimensionally-set group of relations: in particular, each
projected coordinate set in the output configuration will be indistinguishable from
the other three (in the absence of rotations of the solution connected to particular
axial scalings).
zn = 0, each i = 1, n vector of relations contributing equally, ipso
facto, to the group (spatial) structure. Ordinarily MDS is used to probe for internal
structure within a set of similarities (or analogous) data. In such efforts the
dimensional representation serves a similar purpose to the number of factors arriving
in factor analysis. Here, however, we anticipate something more than just unambiguous
representation as a three-dimensionally-set group of relations: in particular, each
projected coordinate set in the output configuration will be indistinguishable from
the other three (in the absence of rotations of the solution connected to particular
axial scalings).
2. The Simulations
Investigation of these concerns proceeded through a series of simulations and empirical pattern analyses [17] designed to determine: 1) whether there is any reason to believe that the kind of natural structure supposed might actually be possible, and if so 2) whether any clear empirical evidence can be produced to support the basic thesis. The simulations came first, and consisted of two distinct series. In the first series, the i-o matrices were stocked with six-digit random numbers; in the second, with summary measures of test patterns imposed on simple geometric surfaces and volumes (later, actual natural world patterns would be examined in like fashion). To simulate the “spatial construction” process, the matrix data were subjected to an entropy maximization operation: again, in this model things do not “happen” “in space”, they happen “as space”; that is, by maximizing entropy through a form of system intra-action common to them all. The entropy maximization technique I applied is known as matrix double-standardization (bistochastization), in which rows and columns of elements are alternately converted to z scores until the matrix values converge to a stable solution. This technique has been used to study, among other things, destination patterns among a set of regions [18] , patterns of faunal region distinctness [19] [20] , identity parameters [21] , and other problems in sociology, ecology, morphometry, political science, botany, etc. The approach has the effect of canceling out the complication of absolute magnitudes of flow or similarity when the matter of interest is relative magnitudes across all elements—as would be the case, for example, when trying to compare rates of commuting among a set of places of greatly differing populations [18] . These results were then contextualized with the aid of MDS: it was determined, as might be expected, that only those matrices that converge to a matrix of z scores that is symmetric about the i = j diagonal can then be projected as an unambiguous (zero-stress) three-dimensional space via MDS, so attention was turned to looking for such solutions among simulated input data.
In this write-up I discuss only the results connected to matrix dimensions of n = 4, but in the actual tests I carried out parallel studies on n = 3, 5, and 6 dimensions as well—but none of these latter investigations produced any results interpretable as three-dimensional space, so are not detailed here [16] [17] . Only those n = 4 solutions that were characterized both by z scores symmetry about the diagonal, and a diagonal consisting of the same four, and highest, z scores passed the “spatial projection” test here, as it seemed illogical to pose the existence of a system one or more of whose subsystems is less similar to itself than it is to another subsystem in the group.
In the first set of simulations, designed to sample the universe of all numerically conceivable combinations of values (and thus of potential flow rates or other kinds of relations), randomly-generated six-digit figures were used to fill the sixteen elements of the initial matrix. Two variations on this basic theme were investigated: 1) four by four matrices consisting of sixteen such values, entirely randomly assigned; 2) the same, but with all i, j values equaling all j, i values. Most recently (in 2008) I ran a total of 40,000 operations under the first set of conditions, and 25,000 under the second. As reported in the other paper [16] the percentages of operations that resulted in symmetric double-standardized results (i.e., that passed the three-dimensionality test) were, respectively: 1) 0.51% (127 of 25,000), and 2) 1.72% (686 of 40,000) (see Figure 1).
These results are both intuitively and logically satisfactory. In each instance the proportion of input matrices that pass the test is small, but not so impossibly limiting as to suggest preclusion of diversity of result altogether (and even more importantly, within-system changes such as would be expected in any non-static natural entity— or for that matter, evolutionary process). Further, that the matrix dimension n = 4 turns out to be the only dimensionality that leads to results passing the test is in keeping with two important facts: 1) that it takes x + 1 coordinate points to specify an x-dimensional geometry; and 2) that equations with five or more variables are almost

Figure 1. Summary of spatial projection simulations for matrix configurations of dimension 3 × 3 through 6 × 6. Circled numbers refer to data at the right margin giving the number of simulations in each test and the standard deviations accompanying the mean values plotted. The plotted numbers are the two pairs of mean correlation type values (see further explanation in Section 3, and [16] ) obtained at each dimensionality (=“no. of classes in classification”). Colored line coding connecting points is for readability purposes only. Point values 17 through 20 are compiled from subsets of the data leading to point values 2, 6, 10, and 14, respectively (after [16] , Figure 1).
never solvable (and here there is exactly only one n = 3 solution that sustains the kind of symmetry required).
The random numbers-based simulations were followed by a series of analyses carried out on contrived twoand three-dimensional test surfaces/figures. The object was to shed light on whether: 1) sets of regularly sampled coordinate points taken off these surfaces/volumes,1 when grouped into four subsets of points and then measured for their summary spatial autocorrelation properties,2 could yield 4 × 4 element matrices that when double-standardized passed the spatial extension test. The geometric surfaces tested included: 1) variously shaped two-dimensional enclosures, each at various “densities” of point sampling (with the sets of coordinates retrieved then randomly grouped into four subsets), 2) same, but sampling coordinate locations from the surface of a sphere, 3) same as #2, but instead of randomly generating subset compilations after the fact, sampling arbitrarily pre-arranged, latitudinally-parallel, hemispherically symmetric zones (with each analysis treating different combinations of widths of the zones), and 4) like #3, but involving samples of concentrically-arranged “zones” within the interior of the sphere (that is, as concentrically arranged about the x, y, z origin within it). These tests yielded a variety of results, though usually with around five percent of the two-dimensional simulations passing the three-dimensionality test, and as many as fifty percent of the three-dimensional simulations doing likewise [22] .
Again, it can be argued that these results appear both intuitively and logically consistent with a priori expectations. In particular, one of the most advanced and complex systems—our biosphere—is organized upon a near-spherical planetary body, and through this kind of modeling an understanding of this might emerge: the pre-existing surface geometry may be such as to facilitate the kinds of stochastically-generated relationships leading to lasting complex structures.
3. Experimental Section: Introduction
Although the model entertained here must by its definition pertain to all naturally-developing systems (and at one level or another, all systems), this is not to expect that all of these will exhibit easily measurable characteristics exposing the supposed cryptic causal influence. Most complex natural systems (especially of smaller scale) are not emergent as, and/or on, simple geometries which are the outcome of neatly reducible causalities: instead, most have convoluted histories that represent reactions to different forces at different times, or to several different forces at once. For systems as complex and advanced as organismal bodies, for example, means of assessing actual information flow rates among subsystems may have to be found before analyses of the type discussed here can be attempted. (On the other hand, secondary characteristics of structures may be amenable to investigation: for example, brain physiology and health as evidenced—spatially—by internally varying temperatures, blood flow, or electrical activity). However, there are some natural systems that do exhibit fairly straightforward characteristics of pattern that can be linked to uniform causal influences, two of these being planetary surfaces and interiors.
Generally speaking, the past century’s increasing knowledge of the interior of the Earth has proceeded through incremental steps, leaning heavily on concurrent improvements both in physical theory and in means of instrumentation-based measurement. This knowledge can be used to present a test of the current model, one which anticipates the presence of structural underpinnings whose discovery would be unlikely through other philosophical starting points.
Before summarizing this research, one further aspect of measurement in the present context needs to be discussed. This concerns the level of redundancy of system structure (or information flow) conveyed through the values in the initial summary matrix, prior to its double-standardization. It is a well-known characteristic of developing natural systems that during their maturation period they tend to develop more and more internal feedback mechanisms that, generally, improve efficiency of operation through the elimination of redundant causal paths (see in particular the writings of the late Eugene and Howard Odum on the maturation of ecological systems). The random numbers simulations discussed earlier make it clear that an infinite variety of configurations of values in the initial summary matrix lead to double-standardized results that pass the three-dimensionality test. Some of these initial configurations may be comprised of individual vectors of values that are on average more highly—or lowly—correlated with the other three, thus exposing varying levels of nonrandomness within any implied corresponding system’s internal differentiation. In this way the mean value of the correlation matrix associated with an initial summary matrix may be considered at the least a measure of the extent of its system’s internal redundancy, and quite possibly, in real world terms, a measure of its net degree of disequilibrium as well (as it works its way toward dynamic equilibrium). Two such “mean correlation” statistics contribute to Figure 1 (see also [16] ).
It is therefore to be anticipated that real world systems measured and sampled as described here might exhibit a variety of nonequilibrial states that yet pass the present “spatial projection” test. Importantly, independent measures of a system’s equilibrium status at various points in its evolution can be expected to correspond to variations over time in its four by four matrix representations, a potentially important means of validation of the overall model. For example, in the studies on the hypsimetric properties of the stream basins [16] we discovered not only that all but one of the basins sampled passed the spatial projection test (with the odd case out only narrowly missing), but that the means of the correlation matrices derived from their spatial autocorrelation scores varied considerably. In an earlier pilot study on another set of stream basins [23] , it was possible to link this variation to independent measures of the basins’ surface energy characteristics (especially, as related to non-normality of elevational profile and other measures indicative of deviation from a system-wide balance between depositional and erosional forces).
4. Experimental Section: Results and Conclusions
In the present example, an attempt was made to contrast the spatial autocorrelation properties of a simulated but simplified zonal earth—a spheroid/geoid consisting of four concentric zones, including a surface zone of uniform width—with conditions obtaining in the actual earth, whose outermost (surface) zone, regardless of how defined (crustal lithosphere, same plus hydrosphere, same plus hydrosphere and atmosphere), varies greatly in thickness below various surface locations. Further, I looked not only at the latter configurations for the present day, but at two periods in the distant past: 95 and 200 million years ago [24] . If in theory the interior zones of the earth really are reflective of a body in (structural) dynamic equilibrium, or very nearly so (see discussion below), then the matrix of spatial autocorrelation coefficients representing inter/intra-zone nearness patterns should 1) produce double-standardized results that pass the three-dimensionality test, and 2) yield a correlation matrix of values whose mean value is both very nearly zero, and likely is smaller than the parallel simulation not taking into account the surface zone’s spatially-varying thickness. Further, it should accomplish these outcomes not only for the present day configuration of the continents, but for those of the two past times (which include system surface zone components—continental masses—whose relative locations, through continuing plate tectonics-based drift, are quite different from those of today). This is arguably a fairly severe initial test.
The three-dimensional sample grid applied assigned about 16,000 to 21,000 within-geoid point locations, depending on the exact initial assumptions. These assignments were then partitioned into the four zonal groups through a combination of programming (based on data from the standard earth model) and estimation: assignment to the top of the mantle or the crust had to be assessed manually, based on the best information I had available.3 The “zone-level” spatial autocorrelation statistics were then calculated (i.e., between and within each i=1,4, j=1,4 pairing of sampled point subsets). Further, the problem was examined under the three different assumptions regarding what constitutes the “surface zone” of the earth (as distinct from the inner core, outer core, and mantle): crustal lithosphere (oceanic plus continental) alone, crustal lithosphere plus hydrosphere, and crustal lithosphere plus hydrosphere plus thirty kilometers of atmosphere. This process was repeated for the data from each of the time periods noted above.
The best overall results were obtained for a surface zone defined in terms of crustal lithosphere alone, but all three configurations for all three time periods both passed the three dimensionality test and yielded mean correlation coefficients ranging in value from about 0.002 to 0.003. An earlier pilot study, using a different set of sampled points at about the same sampling resolution, produced an even lower range of values, from about 0.001 to 0.003 [25] . The simulated data, not accounting for the actual varying thicknesses of the actual surface zone, also passed the three dimensionality test, but produced mean correlation coefficients ranging from about 0.003 to 0.006.
There are two things to be said about these results. First, the range 0.001 to 0.003 represents an extremely small mean correlation value in the present context. In the fully random numbered simulations, only about one matrix in 367 produced mean values as low as 0.001, and one in 81 at 0.003. This, as compared with one in 31 for 0.006. I am unaware of a statistical test for these differences, but clearly the likelihood decreases at a nonlinear rate as zero is approached, so the difference between the actual and simulated data is far greater than it at first appears.
Second, though the degree of precision of sampling here seems considerable (at 16,000 to 21,000 points), it admittedly is still not sufficient to absolutely resolve the matter. In particular, at such low levels of measured spatial disequilibrium even a small amount of sampling bias may work against achieving a fully reliable final assessment. Nevertheless, in the internal differentiation of the earth we have a system of large scale and very long standing whose surface components, at least, provide evidence of having very nearly reached a state of dynamic equilibrium with respect to their participation in primary biogeochemical cycling processes. Atmospheric oxygen, for example, shows no overall trend of increase or decrease over the past three hundred million years (though of course it has experienced several lengthy up and down trends within that period [26] [27] ). Gravity and other natural forces have been equitably shaping the surface as a nearly closed system for so long that it provides an excellent test case for present concerns; one in which internal differentiation of structure is both well-defined (i.e., easy to recognize a priori) and relatively simple to measure. The results reported here, though not yet wholly conclusive, are arguably very suggestive. If the simulations are any guide, the chances of producing three sets of results (out of three attempts starting with vastly differing initial surface patterns) that by chance meet the spatial projection criteria, and are accompanied by correlation matrix mean correlations of 0.003 or under, are vanishingly small.
The uniformity of results across the three time periods is thus both intriguing and consistent with the initial forecast. It can be safely predicted that a more concerted effort, involving perhaps ten or a hundred times as many real world-sampled points, will produce a spatial autocorrelation coefficient matrix whose associated correlation matrix yields a mean value even closer to zero—but that the parallel simulations not taking into account varying thickness will be less affected.
These findings, based on the same fundamental conceptual model as the earlier-discussed stream basins analysis [16] , provide some corroboration for its results. Additional corroboration may be found in several exploratory pilot studies discussed online [28] , including one that looked at variations in earth surface topography (deviation from sea level).
5. Discussion
For over three hundred years, the presumption among scientific investigators has been that space—actually, spatial extension—represents something “within which” matter changes form according to progressive local influences. The concept “within which”, however, is a rather fuzzy one (as the logical positivist Rudolf Carnap discovered when the system described in his Der LogischeAufbau der Welt ultimately collapsed as a result of his inability to provide a satisfactory definition for the elemental notion “located at” [29] ). Here, further evidence is provided for a different view: that space may self-organize—evolve—according to a relatively simple but universal set of rules that underlie all localizations of function comprising it. Within this framework, local complex systems persist for as long as they can maintain an internal, subsystemized routing of information/energy flow of the type described; at the point of “death” the unit dissociates into a large number of less complex ones—molecules or atoms, perhaps—that individually maintain an analogous kind of internal organization at their own level of function. Evidence of such subsystematization may not always be obvious, but the implication is that it is there and can be discovered if we make a concerted effort to look for it.
However skeptical one may be about the underlying philosophical perspective advanced here, the simulations and empirical analyses I have summarized—none of which require great sophistication of analytical technique— seem on their own merits worthy of further development. At the very least they lead one to question some basic assumptions about the role of chance in nature: especially as related to notions of final causes. (Final causes, that is—not first causes. The understanding presented here, while suggesting that the number of physical structures that can possibly evolve is considerably smaller than that is currently assumed, nevertheless still argues for a naturalistic appreciation of that evolution.) Proponents of gaian theory and the anthropic principle should take note.
In view of the simulations and empiricism presented here, the Wallace quote given earlier takes on greater interest. Wallace’s concept of “space” reduces to a statement about the full universe of causal events—whether these are describable in spatially-projected, “three-dimensional”, terms, or not. Here I have presented a model that suggests a way to account for the three-dimensionality of observable nature, but in the same context it becomes interesting to consider whether stable intra-system configurations of subsystemization may exist that are not “spatially projectable”, yet still have causal influence in the overall universe of events.
Wallace was fond of quoting the following words from A Preliminary Discourse on the Study of Natural Philosophy, by Sir John Herschel: “The perfect observer in any department of science, will have his eyes as it were opened, that they may be struck at once with any occurrence which according to received theories ought not to happen, for these are the facts which serve as clews to new discoveries” [30] -[32] . Reported here is a set of data which I feel belong to this category of “occurrence”.
References
- Wallace, A.R. (1894) The Fourth Dimension. Light (London), 14, 467.
- Ehrenfest, P. (1917) In What Way Does It Become Manifest in the Fundamental Laws of Physics that Space Has Three Dimensions? Proceedings of the Royal Academy, Amsterdam, 20, 200-209.
- Whitrow, G.J. (1955) Why Physical Space Has Three Dimensions. British Journal for the Philosophy of Science, 6, 13-31. http://dx.doi.org/10.1093/bjps/VI.21.13
- Tangherlini, F.R. (1963) Schwartzschild Field in n Dimensions and the Dimensionality of Space Problem. Nuovo Cimento, 27, 636-651. http://dx.doi.org/10.1007/BF02784569
- Tegmark, M. (1997) On the Dimensionality of Spacetime. Classical and Quantum Gravity, 14, L69-L75. http://dx.doi.org/10.1088/0264-9381/14/4/002
- Gurevich, L. and Mostepanenko, V. (1971) On the Existence of Atoms in n-Dimensional Space. Physics Letters, 35A, 201-202. http://dx.doi.org/10.1016/0375-9601(71)90148-4
- Barrow, J.D. (1983) Dimensionality. Philosophical Transactions of the Royal Society of London, A310, 337-346. http://dx.doi.org/10.1098/rsta.1983.0095
- Tangherlini, F.R. (1985) Dimensionality of Space and the Pulsating Universe. Il Nuovo Cimento B, Series 11, 91, 209- 217.
- Smith, C.H. (1986) A General Approach to the Study of Spatial Systems. International Journal of General Systems, 12, 359-384, 385-400. http://dx.doi.org/10.1080/03081078608934943
- Smith, C.H. (1987) Note on “A General Approach to the Study of Spatial Systems”. International Journal of General Systems, 13, 285-287.
- Caruso, F. and Moreira Xavier, R. (1987) On the Physical Problem of Spatial Dimensions: An Alternative Procedure to Stability Arguments. Fundamenta Scientiae, 8, 73-91.
- Hosoya, A., Jensen, L.G. and Stein-Schabes, J.A. (1987) The Critical Dimension for Chaotic Cosmology. Nuclear Physics, B283, 657-668. http://dx.doi.org/10.1016/0550-3213(87)90291-4
- Chatterjee, S. (1992) A Class of Multidimensional Cosmological Models and Its Possible Astrophysical Consequences. Annals of Physics, 218, 121-138. http://dx.doi.org/10.1016/0003-4916(92)90270-V
- Callender, C. (2005) Answers in Search of a Question: “Proofs” of the Tri-Dimensionality of Space. Studies in History and Philosophy of Modern Physics, 36, 113-136. http://dx.doi.org/10.1016/j.shpsb.2004.09.002
- Caruso, F. (n.d.) The Three-Dimensionality of the Universe: A Reason for the Existence of Chemists and Beyond. CPBF-CS-004/08.
- Smith, C.H. and Derr, M. (2012) “In Space” or “As Space”?: A New Model. Life, 2, 243-254. http://dx.doi.org/10.3390/life2030243
- Smith, C.H. (2014) The Once and Future Wallace: Simulations: Introduction, and Random Numbers. http://people.wku.edu/charles.smith/once/spa2.htm
- Slater, P.B. (1976) Hierarchical Internal Migration Regions of France. IEEE Transactions on Systems, Man and Cybernetics, SMC-6, 321-324. http://dx.doi.org/10.1109/TSMC.1976.5408783
- Smith, C.H. (1983) A System of World Mammal Faunal Regions. Journal of Biogeography, 10, 455-466, 467-482. http://dx.doi.org/10.2307/2844752
- Smith, C.H. (1984) Areographic Representation of Faunal Characteristics through a “Second-Order” Relational Approach. Evolutionary Theory, 6, 225-232.
- Schoeneich, F. and Klapp, B.F. (1998) Standardization of Interelement Distances in Repertory Technique and Its Consequence for Psychological Interpretation of Self-Identity Plots: An Empirical Study. Journal of Constructivist Psychology, 11, 49-58. http://dx.doi.org/10.1080/10720539808404638
- Smith, C.H. (2014) The Once and Future Wallace: Simulations: A Theory of Spatial Systems. http://people.wku.edu/charles.smith/once/writings.htm#2
- Smith, C.H. (2014) The Once and Future Wallace: Real World Studies II: Stream Basins Morphometry. A: Primary Tests. http://people.wku.edu/charles.smith/once/streams1.html
- Smith, A.G., Smith, D.G. and Funnell, B.M. (1994) Atlas of Mesozoic and Cenozoic Coastlines. Cambridge University Press, Cambridge.
- Smith, C.H. (2014) The Once and Future Wallace: Real World Studies I: Interior Zonation of the Earth. http://people.wku.edu/charles.smith/once/spa1.html
- Lane, N. (2002) Oxygen: The Molecule That Made the World. Oxford University Press, Oxford.
- Berner, R.A., Beerling, D.J., Dudley, R., Robinson, J.M. and Wildman Jr., R.A. (2003) Phanerozoic Atmospheric Oxygen. Annual Review of Earth and Planetary Sciences, 31, 105-134. http://dx.doi.org/10.1146/annurev.earth.31.100901.141329
- Smith, C.H. (2014) The Once and Future Wallace: A Theory of Spatial Systems. http://people.wku.edu/charles.smith/once/writings.htm#2
- Quine, W.V. (1951) Two Dogmas of Empiricism. Philosophical Review, 60, 20-43. http://dx.doi.org/10.2307/2181906
- Wallace, A.R. (1866) The Scientific Aspect of the Supernatural. F. Farrah, London, i.
- Wallace, A.R. (1871) On the Attitude of Men of Science towards the Investigators of Spiritualism. In: Tuttle, H. and Peebles, J.M., Eds., The Year-Book of Spiritualism for 1871, William White, Boston, 28-31.
- Wallace, A.R. (1877) Rise and Progress of Modern Views as to the Antiquity and Origin of Man. In: Report of the British Association for the Advancement of Science 46, John Murray, London, 110-119.
NOTES

1By “regular” sampling I mean maximally packed; that is, six equi-distance nearest neighbors in two dimensions (triangular/hexagonal), and twelve equi-distance nearest neighbors in three dimensions. This approach minimizes possible instances of sampling (and resulting autocorrelation measure) bias introduced by systemic trends in the spatial distribution of the qualities under study.
2The spatial autocorrelation algorithm used involved a metric (as opposed to those based on contiguity considerations) calculation based directly on group-level accumulated sums of squares. Such measures are often proportionalized so they can be compared to other analyses, but this was not done here: firstly, because such comparisons are meaningless within the current framework, and secondly, because the going advice on entropy maximization operations is to begin with the raw measures, not standardized ones (G. J. Daniell, “Of Maps and Monkeys: An Introduction to the Maximum Entropy Method,” pp. 1-18 in B. Buck and V. A. Macaulay, Eds., Maximum Entropy in Action, Clarendon Press, Oxford, UK, 1991).

3My main source of information was the two-degree averaged values appearing on the CRUST 2.0 map by G. Laske, G. Masters and C. Reif (an update of the CRUST 5.1 project), available online at: http://igppweb.ucsd.edu/~gabi/crust2.html. These data were supplemented by a literature search that uncovered a couple of dozen studies that estimated the depth-to-mantle at more local regional scales. Since the sample grid identified locations separated from their nearest neighbors by distances of 275 miles or more, this led to fewer difficult assignment issues than one might initially suppose.

